基于ARIMA和XGBoost算法的煤矿安全态势预测

叶黎明 施式亮，2教授 鲁 义教授 李 贺副教授 曾明圣

(1.湖南科技大学 资源环境与安全工程学院，湖南 湘潭 411100；2.湖南科技大学煤矿安全开采技术湖南省重点实验室，湖南 湘潭411201)

0 引言

进入21世纪，随着我国煤矿事故死亡人数进入稳定下降时期[1]，煤矿安全生产形势逐年向好。2020年我国煤矿事故死亡人数为228人、煤矿百万吨死亡率0.058、瓦斯事故死亡人数30人，死亡人数与1989年的历史最高值7 625人相比下降了97.0%，百万吨死亡率与最高时1949年的22.541相比，下降了99.7%，瓦斯事故死亡人数仅为1997年历史峰值3 800人的0.79%[2-3]。从以上数据可以看出，我国煤矿安全生产形势已经明显改善，但仍应认识到同世界顶尖水平之间的差距。根据美国矿山安全和健康管理局(Mine Safety and Health Administration， MSHA)公布的数据，2020年美国共发生各类煤矿事故29起，共造成5人死亡，百万吨死亡率0.001，分别为同期我国的2%与1.7%。因此分析和预测我国煤矿安全态势，有助于明确煤矿安全态势的发展规律，对促进煤矿安全生产具有重要意义。

煤矿生产系统的安全性受到诸如煤炭资源赋存状态、煤矿开采技术条件、安全投入以及多种致灾因子等系统自身或外部因素影响，因此煤矿生产过程中事故的发生具有多因素时空耦合的复杂性，进而导致表征煤矿安全态势各项指标呈现出较强的非线性特征，仅以单一线性模型刻画重要指标随时间的变化规律存在较大的局限性。针对各项表征煤矿安全态势指标的预测，常用的方法有R/S分析法[4]、灰色预测法[5]、神经网络法[6]、指数平滑法[7]等非线性预测方法。时间序列预测法作为一种重要的非线性预测方法，在道路交通[8]、民航[9-10]、工业生产[11]等领域的安全态势指标预测中得到广泛应用，而运用此方法对煤矿安全态势指标进行预测的研究较少。时间序列预测法采用差分自回归移动平均(Autoregressive Integrated Moving Average Model， ARIMA)、Holt-Winters等模型进行预测，鉴于各项煤矿安全态势指标中所包含的线性、非线性数据将影响单一时间序列模型的预测精度。笔者运用组合预测思想[12]，改善单一模型预测效果。

本文从煤矿安全态势指标时间序列组合预测角度出发，运用ARIMA模型提取各态势指标时间序列的非线性主部，在此基础上，进一步采用极端梯度提升算法(eXtreme Gradient Boosting， XGBoost)，利用该算法预测非线性数据时不易过拟合、泛化能力强的特性对ARIMA模型残差进行修正，从而提高预测精度。基于此，本文建立ARIMA-XGBoost的煤矿安全态势指标预测模型，以期为煤矿安全生产态势指标的预测提供一种新思路。

1 混合模型的构建

1.1 ARIMA模型

ARIMA模型是由Box和Jenkins[13]提出的一种时间序列预测模型，模型包含参数p、d、q，其中p为自回归阶数，d为原始序列平稳化所需的差分阶数，q为移动平均阶数，亦可写作ARIMA(p，d，q)模型。该模型可以通过历史数据对未来进行预测[14]。其建模的基本步骤是根据单位根检验的结果，确定原始序列平稳化所需的差分阶数d，通过分析自相关与偏自相关函数的截尾、拖尾特征，确定参数p、q。模型中，AR是自回归如式(1)所示，MA是移动平均如式(2)所示。

AR(p):Yt=μ+α1Yt-1+α2Yt-2+···+αpYt-p+εt

(1)

MA(q):Yt=μ+β1εt-1+β2εt-2+···+βqεt-q+εt

(2)

将公式(1)与公式(2)结合，再进行d阶差分得到ARIMA(p，d，q)模型，其数学描述可简记为：

式中：

Yt—时间序列中第t项的观测值，t为当前项在时间序列中对应的序号；

ΔdYt—Yt经过d阶差分后得到的观测值；

αi、βi—时间序列中第i项的带估计参数，i是循环变量；

p、q—模型的阶数；

ε—预测残差；

μ—常数。

1.2 XGBoost算法

XGBoost算法是学者陈天奇提出的一种改进的提升决策树(Gradient Boosting Decision Tree，GBDT)算法[15]。它对传统GBDT算法的革新主要体现在2方面，一是XGBoost算法的最终结果是由多棵决策树通过不断的迭代计算之后，再累加而得，在此过程中能充分利用CPU的多线程处理性能，大幅度提升计算速度；二是XGBoost算法通过在目标函数中加入正则化项的方式，简化模型，避免过拟合。以下是它的常规建模过程：

(4)

F={f(x)=ωz(x)}

式中：

xi—第i个数据点的特征向量；

yi—第i个数据点的真实值；

K—决策树数量；

fk—对应决策树空间中的一个函数；

F—回归树的集合空间；

z—特征向量xi映射到树的叶子节点；

ωz(x)—单棵树的预测值。

目标函数包含2部分：

(5)

(6)

此时目标函数可描述为：

(7)

式中：

C—为常数项。

当损失函数l为非平方误差函数时，求解最优解的过程复杂，为简化计算，去掉常数项并采用泰勒展开来近似定义目标函数。

(8)

此时优化后的目标函数：

(9)

其中，Gj=∑i∈Ijgi，Hj=∑i∈Ijhi；Ij为第j棵树每一叶子中的样本集合；目标函数的值越小则树的结构越好[16-17]。

1.3 ARIMA-XGBoost混合预测模型构建

(10)

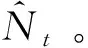
根据ARIMA模型的预测值和XGBoost残差修正值得到混合模型预测值，即

(11)

2 实证计算与分析

2.1 数据来源与处理

本文数据来源于《中国煤炭工业年鉴》[2]与《中国安全生产年鉴》[3]。

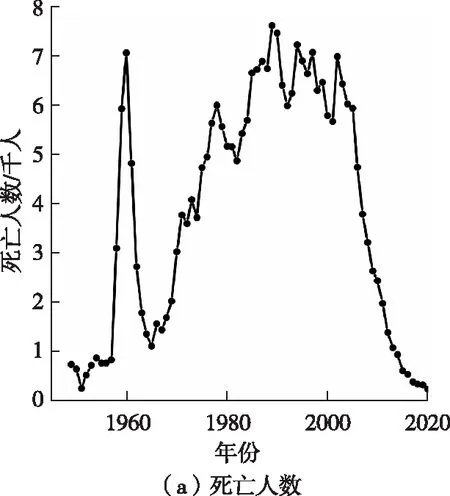
选取1949-2020年煤矿事故死亡人数(以下统称死亡人数)与1966-2020年煤矿百万吨死亡率和瓦斯事故死亡人数的统计数据作为研究对象，以年作为时间步长构建“死亡人数”“百万吨死亡率”“瓦斯事故死亡人数”原始序列，分别用{Ytoll}、{Yrate}和{YGtoll}来表示，如图1。

2.2 ARIMA模型预测

2.2.1 差分阶数的确定

根据图1中的折线变化趋势，初步判断3组原始序列均不符合零均值同方差的特性。3组原始序列单位根检验结果，见表1。由表1可知，{Ytoll}、{Yrate}和{YGtoll}的检验τ统计量分别为-1.098 92、-1.036 28和-1.251 304，均大于各自显著水平10%的临界值，故序列{Ytoll}、{Yrate}和{YGtoll}皆为非平稳序列，需进行差分处理。对3组原始序列一阶差分后得到新序列{△Yrate}、{△Yrate}和{△YGtoll}，再次检验，结果见表2。

表1 单位根检验Tab.1 Unit Root Test

表2 一阶差分单位根检验Tab.2 Unit Root Test after difference

由表2可知，3组序列一阶差分后的检验τ统计量的值分别为-5.322 55、-6.766 90与-8.231 455，均小于显著性水平为1%的临界值，故可判定序列{△Ytoll}、{△Yrate}和{△YGtoll}皆无单位根，序列平稳，已满足了ARIMA建模条件。以序列{△Ytoll}为例对后续建模预测过程进行说明。

2.2.2 最优预测模型的识别

首先，生成序列{△Ytoll}自相关系数(Autocorrelation Function， ACF)和偏自相关系数(Partial Autocorrelation Function， PACF)，如图2。由图2可知，序列{△Ytoll}的自相关系数从第2项开始均在虚线范围内波动，因此可视为1阶截尾；偏自相关系数亦是从第2项开始在虚线范围内波动，也为1阶截尾。由此ARIMA模型的阶数可定为ARIMA(1，1，1)、ARIMA(1，1，0)以及ARIMA(0，1，1)。

图2 “死亡人数”一阶差分图Fig.2 The first difference diagram of "the death toll"

表3为各模型AIC、SC检验值。根据最小信息量准则，选择AIC与SC值都为最小的模型，即ARIMA(1，1，0)为“死亡人数”序列预测的最优模型。按上述过程，“百万吨死亡率”与“瓦斯事故死亡人数”的最优模型为ARIMA(0，1，0)模型与ARIMA(8，1，1)模型。

表3 各模型AIC与SC检验值Tab.3 The AIC and SC value of each model

2.2.3 基于ARIMA模型的关键指标预测

2.3 基于混合模型的预测分析

根据式(10)得出残差序列{etoll}、{erate}与{eGtoll}，在Rstudio软件中调用forecastxgb包实现XGBoost建模。XGBoost算法对3组残差序列的修正值与真实值的对比情况，根据式(11)得出混合模型预测值，如图4。混合模型预测结果与原始序列对比情况，如图5。

单一ARIMA模型、混合预测模型与单一Holt-Winters时间模型对3项指标预测结果的MAPE值，见表4。由表4可知，混合模型的预测结果相较于单一ARIMA模型、Holt-winters模型在预测精度上均有提升，混合模型“死亡人数”与“煤矿百万吨死亡率”的MAPE值分别为14.121%与10.302%，混合模型对“瓦斯事故死亡人数”这一指标的预测精度提升最为明显，从单一ARIMA模型20.496%，降至12.728%，预测精度提升了37.9%。

表4 3种模型的MAPE值Tab.4 The MAPE value of three models

进一步使用ARIMA-XGBoost混合模型对2021年3项指标的预测结果，见表5。

根据表5中的数据，2021年我国煤矿事故死亡人数约为151人与煤矿百万吨死亡0.048 17，2项指标相较于2020年分别下降33.8%与16.9%，预测结果符合近几年来煤矿安全生产形势逐年向好的大趋势。值得注意的是，瓦斯事故死亡人数的预测值约为59人，接近2020年的2倍，虽呈现较强的反扑态势，但也符合2017年以来我国煤矿瓦斯事故死亡人数表现出的增减交替，波动下降的总趋势，因此煤矿安全管理部门仍需加强对高瓦斯煤矿的监管工作。2021年作为煤矿安全生产专项整治“三年行动”承上启下的关键一年，进一步改善煤矿安全生产形势，可借助煤矿智能化开采、淘汰不具备安全开采条件的矿井等举措。

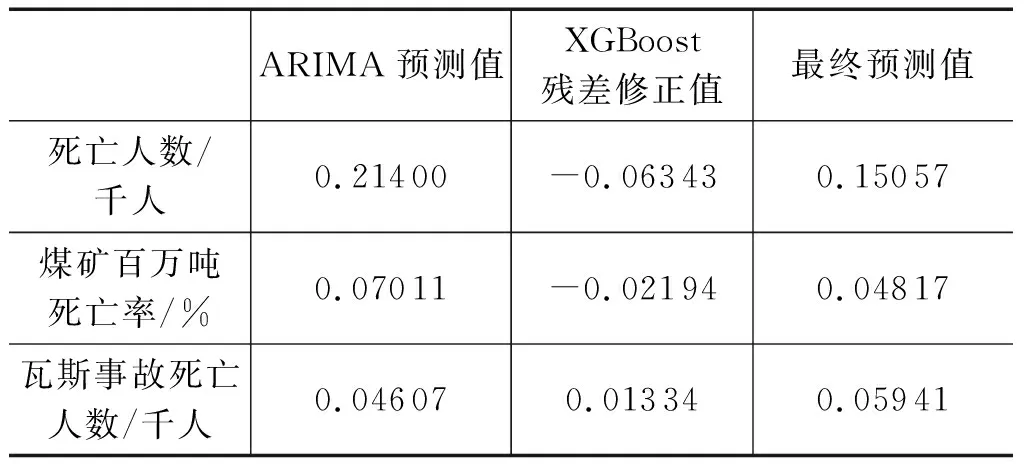
表5 2021年3项指标预测值Tab.5 Predictive values for three indicators in 2021

3 结论

(1)为充分挖掘煤矿安全态势指标时间序列自身演变信息，在运用ARIMA模型提取时间序列非线性主部的基础上，进一步利用XGBoost算法修正预测残差，建立ARIMA-XGBoost煤矿安全态势指标混合预测模型。使用该混合模型对3项煤矿安全态势指标进行预测，预测结果的MAPE值均低于单一ARIMA、Holt-Winters模型，因此该混合模型更适用于对煤矿安全态势指标的预测。

(2)根据ARIMA-XGBoost混合模型的预测结果，2021年我国煤矿事故死亡人数与煤矿百万吨死亡率将继续保持下降趋势，进一步降低煤矿事故死亡人数必须依赖于智能采煤工作面等新技术的应用。对于瓦斯事故死亡人数这一指标的抬头趋势，煤矿安全管理部门继续加强整治力度，减少瓦斯突出、瓦斯爆炸等事故的发生。