基于物元模型的古建筑木结构健康诊断与安全评价研究*

2022-03-24张锦川张荣献

林产工业 2022年3期

王飞谭征张锦川张荣献王威

（1.南阳理工学院，南阳市人居节能重点实验室，河南南阳 473004；2.南阳市防震减灾中心，河南南阳473005;3.北京工业大学抗震减灾研究所，北京 100124）

我国古建筑是中华民族几千年文明发展史的重要载体，具有不可替代的资源特点与深厚的历史研究价值[1]。根据全国文物第三次普查成果显示，我国登记不可移动文化约76.67 万处[2]，其中：保存状况较差的占比17.77%，保存状况差的占比8.43%，且近50%均为木结构形式。这些古建筑木结构在长期使用过程中，由于环境侵蚀、自然灾害与人为因素共同作用下，出现屋面漏雨、木构件拔榫及墙身松散等病害状况，导致安全状况进一步退化[3]。因此，对现存古建筑木结构的健康诊断与维护，是保护我国历史文化遗产的重要举措。

古建筑木结构的建造方式较为复杂，不同类别的木结构残损类型对结构、构件安全性等影响程度不同[4]。当前，古建筑木结构的健康诊断与安全等级评价，主要以定性鉴定为主、辅以定量评价相结合的方法展开[5]。Cointe等[6]在现场测量与数值耦合模拟的基础上，提出一种对古木质框架结构健康进行评价的方法。Garziera等[7]利用干涉雷达无损技术对古建筑健康状况进行检测与评价，李宁等[8]采用概率法对古建筑木结构进行安全评价，张德军等[9]在现场检测的基础上，利用有限元建模对上海古建筑住宅进行安全评价研究。石若利等[10]利用ABAQUS分析木结构节点加固性能情况，为木结构抗震加固基受损后修缮提供借鉴。禤示青等[11]利用ABAQUS建立有限元模型，对燕尾榫连接胶合木梁的抗弯性能进行研究。Lima等[12]应用光纤光栅传感器对阿威罗达任凭教堂的结构健康进行了监测与评估。上述研究成果对古建筑木结构安全评价提供有益借鉴，但如何对其安全性影响因素进行量化分级及反映各因素之间相关性，并提出合理评价与维护措施，仍需进一步探讨。鉴于此，本文依据物元分析理论，将古建筑木结构的健康状态、评价指标与相应的特征值作为物元，通过得到模型的经典域、节域、权系数与关联度，进而构建古建筑木结构健康诊断与安全评价物元模型，并通过实例验证合理性。

1 古建筑木结构安全评价的物元模型

物元分析理论是系统科学与思维科学的交叉学科，它可以通过建立评价多指标性能参数的质量评定模型，以定量的数值来表征评定结果，从而能够较系统地反映事物质量综合水平。相比灰色理论、模糊数学等方法，物元模型具备简洁明了及计算量小的特征。因此，被广泛应用在矿山生产安全、环境健康评价、电网发展诊断与地铁盾构风险评价等诸多领域[13-16]。

1.1 物元模型概念界定

假定待评木结构为N，其安全特征C的量化值为V，则其有序的三元组R=(N,c,v)可作为描述N的基本元，即称为物元[17]。若N有多个量化特征，且以n个c1,c2,…cn与相应的量化值v1,v2,…vn进行描述，则可如下表征：

式中：R为n维木结构安全物元，记为R=(N,c,v)。

1.2 确定模型经典域及节域物元矩阵

古建筑木结构安全的经典域物元矩阵可表征为：

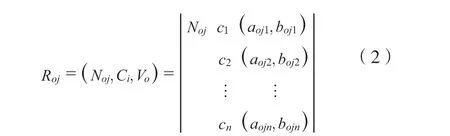
式中：Roj为经典域物元；Noj为所划分木结构安全的第j个评价等级，j=(1,2,…n)；ci为第i个评价指标；(aoj1,boj1)为对应评价等级的量化区间范围，即经典域。

则古建筑木结构安全的节域物元矩阵可表征为：

式中：Rp为节域物元；vpi=(api,bpi)为节域物元Rp特征ci的量化区间；p为古建筑木结构安全评价等级，一般取值范围为Ⅰ～Ⅴ。

1.3 确定待评对象物元

可将待评对象Nx的物元表征为Rx，即：

1.4 确定关联函数与关联度

古建筑木结构安全评价指标的关联函数K(x)可定义为：

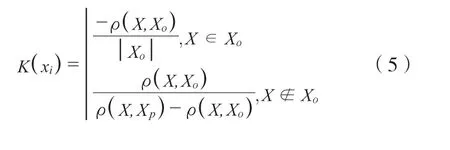
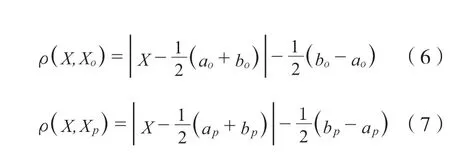
式中：ρ(X,Xo)为点X和有限区间Xo=[ao,bo]之间的距离，mm；ρ(X,Xp)为点X和有限区间Xp=[ap,bp]之间的距离，mm；且有|Xo|=|bo-ao|，X,Xo,Xp分别表征为待评木结构安全物元、经典域物元与节域物元的量化区间范围，一般取[0,1.00]。

1.5 确定综合关联度及评价等级

可将待评对象Nx的等级j的综合关联度Kj(Nx)定义为：

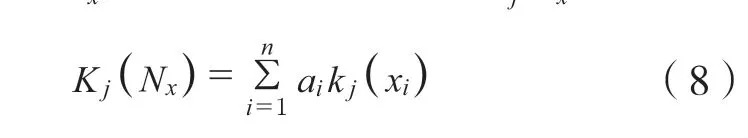
式中：Kj(Nx)为待评对象Nx的综合关联度；kj(xi)为待评对象Nx的单指标关联度；j-(1,2,…m)、ai为各待评指标的权重值，取值范围为[0,1]。若有：

式中：Kji为待评对象Nx第i个指标j等级的关联函数；Kjx为待评对象Nx的最大综合关联度取值。

物元模型的关联度函数k(x)在实数轴上的大小，实际上表征待评对象属于木结构安全水平标准的程度大小，可将逻辑值从[0,1]闭区间拓展到(-∞,+∞)，相比模糊数学理论的隶属度，能揭示出更多分异信息，所代表的内涵属性更为丰富[18]。当k(x)≥1.0时，表征代评对象Nx超过了相应标准对象的上限值，其数值越大，对应的开发潜力越大；当0≤k(x)＜1.0时，表征代评对象Nx符合等级标准的程度要求，其数值越大，越接近标准的上限值；当-1.0≤k(x)＜0时，表征代评对象Nx不符合标准对象要求，但具备转化标准的条件，其数值越大，越容易转化；当k(x)＜-1.0时，表征代评对象Nx既不符合标准对象要求，也不具备转化标准的条件。

2 实证研究

为表明物元模型应用于古建筑安全评价具备科学性及适用性，以青城山皇帝殿[19]为例进行仿真研究，该殿建于隋代，全高11.07 m，为砖木、石的混合结构，整栋建筑有四种不同材质与形状的柱子，底层左侧墙裙是50 mm厚的石板，右侧墙裙为木板，由于汶川地震前该殿并未按照地震监测仪器，因此，通过现场实测与软件分析相结合的方法，用Midas-gen软件建立了该殿的有限元整体抗震模型，如图1所示。详细指标与测试数据参见文献[19]。

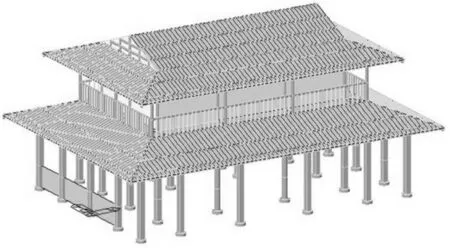
图1 皇帝殿有限元整体模型Fig.1 Overall finite element model of Huangdi hall

2.1 确定指标体系与评价因子

建筑地震破坏类型的划分，应以建筑遭受地震破坏为主要依据，由于古建筑木结构具有中低烈度地震非结构易损性、高烈度地震结构整体抗倒塌性的特征，并可能出现榫卯拔脱、基础破坏等多种震害特征[20-21]。一般来讲，古建筑木结构破坏等级主要有三种：以建筑或构件的破坏评估等级；以建筑或构件破坏程度+破坏易修复程度评估等级；以构件破坏程度等级+破坏易修复程度评估等级等。考虑到地震发生时，古建筑木结构呈现出小震下易损坏性与大震下的抗倒塌性，以古建筑木结构震害变形、残损、构件承载能力及修复难易程度为基准，郇君虹等[22]结合历史震害资料及相关实验研究，给出了震害等级及古建筑木结构健康状态、结构破坏特征及维修措施的对应关系，详见表1。

表1 古建筑木结构健康状态、结构破坏等级及维修措施Tab.1 Health status, structural damage level and maintenance measures of ancient wooden structures

针对古建筑的健康诊断与安全性评价工作，有关单位相继颁布了GB/50023—2009《建筑抗震鉴定标准》、GB/T50165—2020《古建筑木结构维护与加固技术规范》等标准，多采用评级法或残损点法对古建筑结构进行安全评价，一般把古建筑木结构指标体系分为上部结构、基础与地基三个层级进行设计，即目标层、准则层、指标层，借鉴以往研究，有效筛选出具有代表性、独立性与易于区分的九项古建筑安全评价指标因子集[19,21]，如图2 所示。

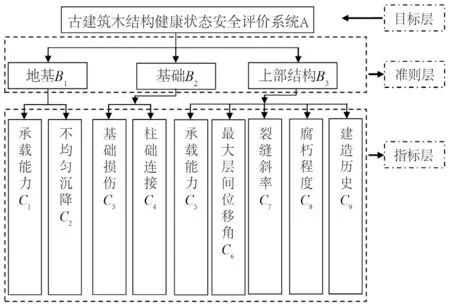
图2 古建筑木结构健康状态安全评价系统Fig.2 Health and safety evaluation system of ancient wooden structures

2.2 确定各评价因子的评定标准

针对古建筑的健康诊断与安全性评价工作，国家与地方单位相继颁布了规范标准，多采用评级法或残损点法对古建筑结构进行安全评价，一般把古建筑木结构分为鉴定单元、结构子单元与单个构件三个层级，并将其依据安全性分为A、B、C、D四个等级，但并未考虑相应检测项目的权重值。古建筑木结构安全性能评价影响因子众多，且有的因子呈现出一定的模糊性、区间性与非线性等特征。为精确量化各评价因子属性区间特征，鉴于上述物元模型的建模量化分析，及相应的分级标准及工程实践经验[23-26]，分别给出古建筑木结构地基承载力、不均匀沉降、基础损伤、柱础连接及上部结构等各因子的物元评定标准，其中：地基承载能力C1（kPa）与不均匀沉降C2（mm）的划分标准为不均匀沉降的允许差值或者建筑物连续两个月地基沉降裂缝值等；基础损伤C3（%）与柱础连接C4（%）的划分标准为建筑物基础损伤程度等；上部结构承载能力C5（kPa）、最大层间位移角C6（%）、裂缝斜率C7（%）、腐朽程度C8（%）及建造历史C9（a）的划分标准分别为：承载力值、层间位移角值、裂缝斜率值、挠度值、截面腐朽面与整体截面面积之比值及建造期限等，并结合古建筑木结构安全的经典域物元，赋以相应的模型节域范围。详见表2～4。

表2 地基因子的物元评定标准Tab.2 Matter element evaluation standard of foundation factor

表3 基础因子的物元评定标准Tab.3 Matter element evaluation standard of basic factors

表4 上部结构因子的物元评定标准Tab.4 Matter element evaluation criteria for superstructure factors

2.3 评价因子数据集成

为了对青城山黄帝殿进行安全评价，收集梳理了汶川地震后该殿的结构健康状态评价因子数据[19]，详见表5。

表5 皇帝殿结构健康状态诊断综合评价因素的指标值表Tab.5 Index value table of comprehensive evaluation factors for structural health diagnosis of Huangdi hall

2.4 模型数据量化预处理

由于各评价指标的量化值所在的区间不完全相同，有的评价指标是数值越小，健康状态越好，而有的则相反。因此，需要对各评价指标和评价标准进行归一化处理。对于极大型评价因子，有如下公式：di=(Xi-Xmin)/(Xmax-Xmin)；对于极大型评价因子，则有：di=(Xmax-Xi)/(Xmax-Xmin)，式中所表示的分别为归一化处理后的标准值、未归一化处理的标准值，以及模型节点域区间的最小、最大标准值。经过归一化处理后的青城山皇帝殿结构健康状态诊断综合评价因素的指标值、评价标准，分别如表6 与表7 所示。

表6 归一化后的皇帝殿结构健康状态诊断综合评价因素的指标值表Tab.6 Index values of normalized comprehensive evaluation factors for structural health diagnosis of Huangdi hall

表7 归一化后的各评价因子的评定标准值表Tab.7 Evaluation standard values of normalized evaluation factors

2.5 确定模型经典域与节域

基于上述建模分析，利用公式（4），确定模型经典域与节域如下：

2.6 确定模型权系数与综合关联度

基于上述建模分析，利用公式（7），确定模型权系数如表8 所示。

表8 模型权系数表Tab.8 Weight coefficient table of the model

根据公式（5）、（6），计算模型综合关联度以及相应的青城山皇帝殿结构健康状态诊断结果：KI(P)=-0.257；KII(P)=-0.226；KIII(P)=-0.175；KIV(P)=-0.459；KV(P)=-0.547。

由此可知：KIII(P)=maxKj(P)，j=I～V，其诊断结果为Ⅲ级，即青城山皇帝殿汶川地震后的结构健康状态为差，其破坏等级为中等破坏，针对其破坏情况，需要对其少数主要构件进行加固处理，这与基于层次分析法与模糊数学理论等评价方法，得出的皇帝殿主要部分处于中等程度破坏的评价结果一致[19,27,28]，详见表9。皇帝殿实际震后破坏情况为：建筑主体基本完好，柱础连接损坏，部分构件出现拔榫等状况，与物元模型的评价结果基本相符。因此，震后可对皇帝殿采取砖柱更换、构架纠偏、木构件修缮与节点加固等措施。