加锚异质岩层压剪脱黏破坏及锚固失效机理分析
2022-03-24赵增辉陈宝森冯元慧
赵增辉,陈宝森,冯元慧,孙 伟,刘 浩
(1.山东科技大学 能源与矿业工程学院,山东 青岛 266590;2.山东科技大学 矿山灾害预防控制省部共建国家重点实验室培育基地,山东 青岛 266590)
复合岩层在矿山顶板中较为常见,由于岩层间力学参数差异较大,层间黏结力低,致使煤炭开采过程中顶板离层、垮落、失稳事故常有发生。锚杆支护作为1种高效、经济的支护手段在矿山工程中具有广泛应用。针对顶板锚杆的悬吊作用和组合梁效应以及岩层离层引起的锚杆拉断破坏已取得了大量的成果[1-4]。然而,复合顶板锚固过程中,锚杆穿越不同岩层时由于顶板下沉和层间滑移引起的锚杆折弯破坏已在工程中大量被发现[5-9],但相关研究成果还比较少。
近年来,国内外学者针对锚杆在岩层中的加固机制进行了大量的理论、试验和数值模拟研究。如从理论方面提出了横向剪切变形段长度的计算方法[10-13],考虑岩层间的横向剪切滑移,建立了含软弱界面复合软岩锚固的力学模型[14-15],基于室内试验建立了预测不同粗糙度条件下锚杆抗剪性能的无量纲数学模型[16],考虑软弱夹层建立了巷道预应力围岩强化组合梁的本构模型[17]。在试验方面则通过锚固节理岩体的实验室压剪试验,讨论了岩体强度、节理面法向应力等因素对加锚节理岩体剪切力学特性的影响[18-20]。此外,研究人员通过建立节理岩体锚固的有限差分模型[21]、有限元模型[22-23]和颗粒流模型[24],从宏观、细观不同角度揭示了节理岩体锚固效应的各类影响因素和相互作用规律。
目前国内外关于加锚岩体锚固研究主要集中在节理岩体,针对异质复合岩层锚固方面的成果较少。为此,研究构建了锚杆-黏结层-岩层的精细化压剪数值计算模型[25-26],分析了异质岩层不同组合下锚杆、黏结层及岩层的荷载传递和变形破坏特征,相关结论对弄清矿山顶板穿层锚固失效机制及复合顶板灾害防控具有重要意义。
1 加锚复合岩层锚杆变形过程
加锚复合岩层锚固示意图如图1。
在水平荷载和垂直荷载作用下,随着岩层横向变形的增加,层理面附近的锚杆将经历弹性、弹塑性、完全塑性3个变形阶段。当剪切位移较小时,锚杆产生弹性变形(图1(a)),锚杆抗剪力和黏结层与岩石界面的胶结力共同抵抗岩层的剪切滑移;随着剪切位移的增加,在距离层理面一定距离处,锚杆产生塑性铰(图1(b)),锚杆进入弹塑性变形阶段,随着剪切位移的增加,锚杆塑性区由起塑位置向层理面不断靠近,该段锚杆本身承担大部分的横向剪切力,成为抗剪作用的主体,在由弹性到塑性的过渡过程中锚杆受到的各种载荷错综复杂;当塑性区扩展到层理面附近,锚杆局部进入完全塑性阶段(图1(c)),其强度极限是评判锚杆锚固性能的重要指标。

图1 锚杆拉剪变形过程示意图Fig.1 Shear deformation diagrams of rock bolt
2 加锚异质岩层压剪数值计算模型
2.1 锚固系统本构模型
2.1.1 岩层屈服准则
基于ABAQUS建立数值计算模型,为避免M-C模型屈服面的尖角导致塑性流动方向不唯一,采用连续光滑的流动势函数拟合三维空间中不规则的六角形截面角锥体,屈服面函数G为:
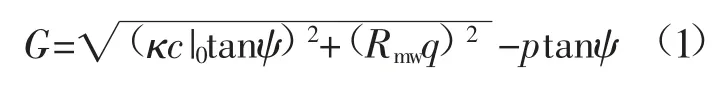
式中:ψ为子午面上高围压时的剪胀角;c|0为初始黏聚力;p为静水压力;q为Mise等效应力,κ为定义流动势函数在子午面上,一般取0.1;Rmw为偏应力系数。
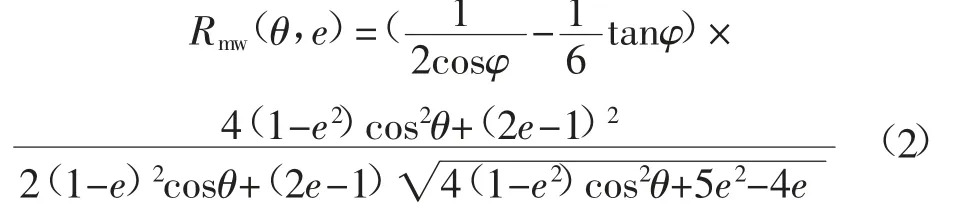
式中:φ为材料的内摩擦角;θ为偏极角;e为流动势函数在π平面上的形状参数,椭圆形屈服面的外凸和光滑要求0.5<e≤1.0。
2.1.2 黏结层损伤模型
引入混凝土损伤模型模拟黏结层损伤开裂行为,简单应力状态下混凝土的应力-应变如图2。混凝土材料单轴受拉和受压时,在达到失效应力之前为线弹性,刚度不变,而进入软化阶段后将产生刚度劣化。

图2 简单应力状态下混凝土的应力-应变图Fig.2 Stress-strain relation of concrete under simple stress state
假设E0为初始(未损坏)弹性刚度,则单轴拉伸和压缩载荷下的应力σ-应变ε关系可表示:
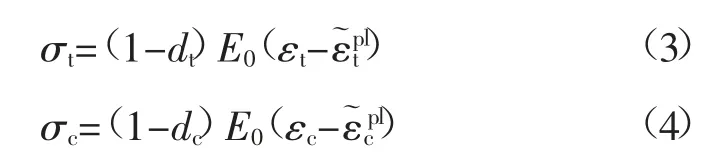
dc和dt可定义为等效塑性应变和、温度T和场变量fi的函数:
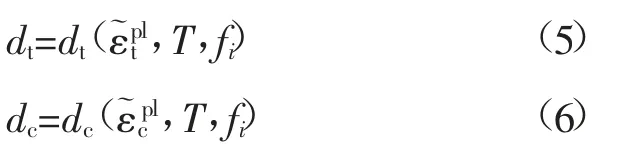
2.1.3 锚杆双线性强化模型
采用双线性强化本构模型描述锚杆的变形特性,锚杆双线性强化本构模型如图3。

图3 锚杆双线性强化本构模型Fig.3 Bilinear constitutive model of rock bolt
图3本构模型中,OA为弹性阶段,AB则综合了材料屈服阶段和强化阶段的性质。在简单拉伸的变形条件下,材料后继屈服限σs与先期拉塑性应变εp的关系为:

式中:h为材料的塑性模量;dεp为先期累积塑性应变值。
2.2 数值计算模型
锚固系统数值模型如图4。上下岩层尺寸均为150 mm×150 mm×75 mm,黏结层厚度为3 mm,锚杆直径为12 mm,长度为145 mm。岩石、黏结层和锚杆选用C3D8R实体单元,通过布置局部种子以及切分模型的方式将锚杆附近的网格进行加密处理,节点总数为2 859个,单元总数为1 928个。

图4 计算模型图Fig.4 Calculation model diagram
为分析异质岩层锚固力学行为,设置花岗岩-花岗岩(H-H)、花岗岩-砂岩(H-S)、砂岩-花岗岩(S-H)以及砂岩-砂岩(S-S)4类参数。锚杆力学参数为:①弹性模量:200 GPa;②泊松比:0.3;③屈服强度:413 MPa;④抗拉强度:575 MPa。岩层参数见表1,黏结层力学参数见表2。

表1 岩层参数Table 1 Mechanical parameters of rock

表2 黏结层力学参数Table 2 Mechanical parameters of bonding layer
2.3 边界条件与接触行为
模型前后限制z方向位移,左右面限制x方向位移。采用分级加载方式,首先在岩层1上部施加法向荷载F=3 MPa,然后在左侧施加横向载荷Q,分4次进行逐级加载,每次为2 MPa,总计8 MPa。岩石、黏结层和锚杆之间的接触面法向作用均设为“硬”接触,切向作用采用罚摩擦公式。各接触面的摩擦系数如下:①砂岩-砂岩(S-S)接触面:0.364;②花岗岩-花岗岩(H-H)接触面:0.303;③砂岩-花岗岩(S-H)接触面:0.333;④砂岩-黏结层接触面:0.600;⑤花岗岩-黏结层接触面:0.600;⑥锚杆-黏结层接触面:0.700。
3 结果分析与讨论
3.1 岩层-锚杆荷载传递规律分析
岩层-锚杆接触应力变化规律如图5。
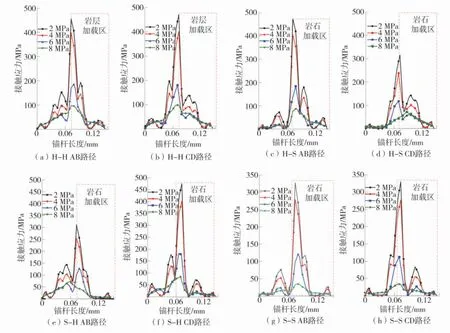
图5 岩层-锚杆接触应力变化规律Fig.5 Contact stress diagrams of rock and rock bolt
由图5可知,在水平和垂直荷载作用下,锚杆首先进入弹性阶段,锚杆抗剪力与岩石界面的胶结力共同抵抗岩层的剪切变形,加载到2 MPa时岩层-锚杆接触应力大小排序为:H-S≈S-H>H-H>SS,这说明异质岩层层理面处的胶结力小于同质岩层的。S-H、H-S、S-S在加载到4 MPa时锚杆进入弹塑性阶段,H-H在加载到6 MPa时锚杆进入弹塑性阶段,这说明岩石强度越大越能发挥锚杆的强度。在弹塑性阶段,岩层-锚杆荷载传递的最大接触应力区主要分布在层理面附近,锚杆本身承担大部分的横向剪切力,成为抗剪作用的主体。在完全塑性阶段,锚杆产生明显变形。H-S中AB路径处的接触应力峰值明显大于CD处接触应力峰值,S-H中AB路径处的接触应力峰值明显大于CD处接触应力峰值,这说明岩层-锚杆接触荷载大小与岩石的排列组合有关。
3.2 不同岩性组合下锚杆应力分布特征
锚杆正应力在不同岩性组合下的分布规律如图6。锚杆切应力在不同岩性组合下的分布规律如图7。

图6 锚杆正应力在不同岩性组合下的分布规律Fig.6 Distribution law of rock bolt normal stress under different lithologic combinations
由图6可知,4种模型中锚杆正应力均存在2个极大值和2个极小值,在层理面两侧波峰和波谷交叉出现,层理面正应力接近0。最大拉应力的排序为:S-S>H-S≈S-H>H-H;最大压应力的排序为:SS>S-H≈H-S>H-H。在同质加锚岩体中,锚固软岩层的锚杆最大拉压应力都要大于硬岩层中的。这说明锚杆在软岩层中更易发生破坏,对抗拉压强度的要求更高。
由图7可知,4种模型中的锚杆切应力均存在3个极大值和2个极小值,波峰和波谷交叉出现,在层理面附近存在最大值。锚杆轴线上最大切应力区域主要位于在岩层层理面处。切应力的排序为:S-S>H-S≈S-H>H-H,这说明岩层强度越低,结构面处的锚杆强度要求越高,且H-S和S-H的结果近似,锚杆切应力峰值受岩层岩性组合的影响较小。

图7 锚杆切应力在不同岩性组合下的分布规律Fig.7 Distribution law of shear stress of bolt under different lithologic combinations
3.3 不同岩性组合下岩石变形破坏分析
岩层1整体水平位移随载荷步的变化规律如图8。岩层塑性区应变示意图如图9。
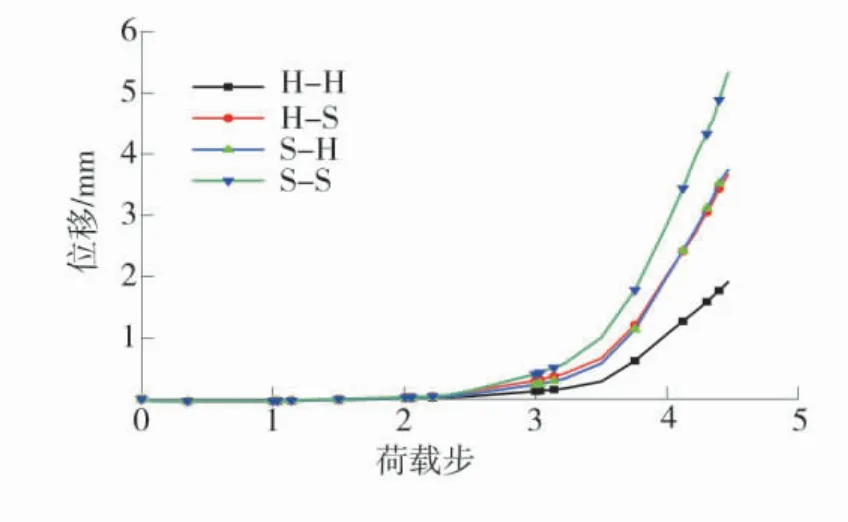
图8 岩石1整体水平位移随载荷步的变化规律Fig.8 Variation diagram of overall horizontal displacement of rock 1 with load step
由图8可知,随着横向载荷增加,岩层整体位移逐渐增大,位移增速提高,排序为:S-S>H-S≈S-H>H-H,说明相同的边界条件下,同一锚杆锚固同质硬岩层的效果最好,同质软岩层的效果最差,异质岩层的效果介于两者之间。
由图9可知,塑性区的分布状态与岩层的岩性密切相关。对于同质岩层,塑性区在两岩层内部均有存在。H-H中的塑性区范围和塑性应变量都要小于S-S。对于异质岩层来说,塑性区仅存在于软岩层中,硬岩层中只有弹性变形。H-S和S-H中的塑性区范围和塑性应变量相差无几,但是它们的塑性应变的峰值要大于S-S,这说明H-S和S-H相较于H-H和S-S,硬岩更难发生破坏,软岩更易发生破坏且变形量更大,所以在锚固异质岩层的时候应重视软岩的变形行为。

图9 岩石塑性区示意图Fig.9 Schematic diagrams of rock plastic zone
3.4 不同岩性组合下锚固系统脱黏破坏特征
锚杆锚固作用的失效除了与锚杆强度、锚杆与黏结层的脱黏外,还与黏结层自身破坏有关。选取黏结层中靠近层理面的A、B 2个单元来分析。随横向载荷的施加,单元自身损伤程度的变化,用刚度折减率来衡量,A、B单元刚度折减率变化规律如图10。由图10可知,S-H中A点刚度折减率总是大于H-S中A点刚度折减率,而B点刚度折减率演化则相反,这说明在异质岩石中刚度折减率大的单元总位于较软的岩石中,岩石强度越小对锚杆抗剪能力的折减率越高,加固效果越差。
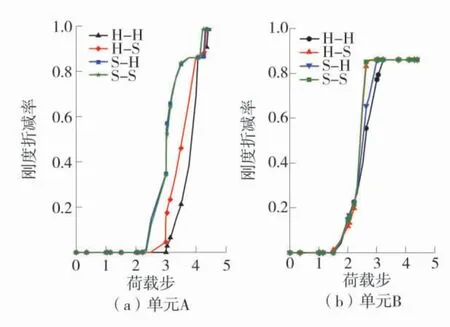
图10 A、B单元刚度折减率变化规律Fig.10 Variation of stiffness reduction rate of element A and element B
H-H下岩层、黏结层和锚杆的变形破坏图如图11,由图11可知,在层理面左下和右上方向出现2个变形破坏区,锚杆与黏结层之间相互分离,产生脱黏破坏行为,黏结层与岩石之间发生相互挤压与分离,失去黏结作用。

图11 变形破坏图Fig.11 Deformation failure diagram of rock-bonding layer and rockbolt
岩石、黏结层和锚杆的AB方向和CD方向水平位移量如图12和图13。
由图12和图13可知,岩石、黏结层、锚杆的层理面附近产生非协调水平位移,相比较而言,锚杆与黏结层在软岩中更易发生脱黏现象。脱黏破坏的内在机理为在横向载荷作用下岩石和锚杆从内外两侧对黏结层施加压力,它们沿锚杆轴线方向的分量使层理面附近的黏结层发生弯曲变形,导致该处的两接触面的间隙不为0,相应节点的接触约束被解除,便产生脱黏破坏行为。

图12 岩石-黏结层-锚杆界面AB方向水平位移Fig.12 Horizontal displacement AB of rock-bonding layer and rockbolt
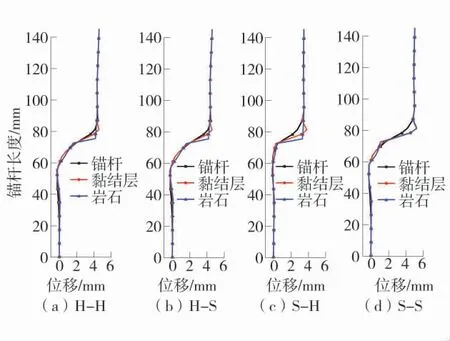
图13 岩石-黏结层-锚杆界面CD方向水平位移Fig13 Horizontal displacement CD of rock-bonding layer and rockbolt
4 结 论
1)异质加锚岩体锚杆正应力分布与锚杆的穿层顺序有关;锚固软岩的锚杆最大拉压应力都要大于硬岩的,这说明锚杆在软岩中更易发生破坏,对抗拉压强度的要求更高。同时,4种模型中的锚杆切应力峰值受岩性组合的影响较小。
2)在同一边界条件下,锚杆限制同质硬岩的移动效果最好,同质软岩的效果最差且锚杆与黏结层在软岩中更易发生脱黏现象,异质岩石的效果介于两者之间。就限制岩层横向移动来说,异质岩层的锚固效果与岩性组合无关。
3)岩石内部塑性区的分布状态与岩石的岩性密切相关,塑性区的形状大致呈“漏斗”型。H-H中的塑性区范围和塑性应变量都要小于S-S。H-S的塑性应变的峰值要大于S-S。异质岩石相比于同质岩石,其硬岩部分更难发生破坏,软岩部分更易发生破坏。
4)锚杆锚固后,异质岩石中刚度折减率大的位置总位于其软岩部分,岩石强度越小对锚杆抗剪能力的折减率越高,加固效果越差。
