基于直流电压维持法的TSC投切电路研究
2022-03-23张俊岳倩倩蒋龙云
张俊,岳倩倩,蒋龙云
(安徽三联学院 电子电气工程学院,安徽 合肥 230601)
0 引言
配电网中用电负荷的功率因数通常低于1,而且三相用电负荷不平衡,电网侧如果不能快速提供用电负荷所需要的无功功率,就会降低电网质量,对电网产生不利影响[1]。为达到电力公司的功率因数要求,用户通常会选择无功补偿装置来提供自身所需无功功率。应用较广泛的无功补偿装置有SVC(静止无功补偿器)和SVG(静止无功发生器)。TSC(晶闸管投切电容器)是SVC中的典型,以其低成本和可靠耐用的优势占用较大市场份额,但是这种补偿装置的响应速度已经不能满足电焊机、缝焊机及点焊机等快速变化型负荷的需求[2];动态无功补偿装置如TSC与SVG协同工作的混合补偿装置能够实现动态补偿,有更快的响应速度,但其成本比同等容量的SVC更高[3-4]。
为实现TSC装置中补偿电容快速无冲击投入电网,目前已对TSC主电路有大量研究。但现有研究都是在传统的无源器件搭建的补偿主电路基础上展开的,无法避免传统主电路中存在的固有问题,不能够完成在一个系统周期内投切,且投切时机发生在准过零点上,会导致较大的冲击电流,严重时还可能因电流过大烧坏晶闸管。因此本文提出一种加入有源器件的主电路形式,可实现补偿电容无冲击电流快速投切。
1 传统主电路中的固有问题
TSC主电路有多种拓扑结构,在380 V低压电网的配电系统中,多采用三角形角内接法[5]。在工程应用中,无功补偿使用的晶闸管通常指由两个反并联的晶闸管封装在一起的晶闸管阀VT,采用分析单相电路模型的方法分析三相电路,单相电路模型如图1。图中忽略电路中的电阻,L表示系统所有电感,C表示电容器组的电容。

图1 传统TSC单相电路模型
假设AC电压源是标准的正弦信号,晶闸管为理想开关,忽略其导通压降和开关损耗,根据基尔霍夫电压定律,列出电压方程并求解,得到“无冲击电流投切”条件:

上式中,α为触发角,UC0为电容器组残压,Um为电网电压峰值,λ为自然角频率和基波角频率的比值。为满足以上条件,现行的方案是在晶闸管两端加过零检测电路,当晶闸管两端电压接近零且晶闸管承受正向电压时,可以进行无冲击电流投切[6]。

要使电容器残压等于电网电压峰值,则λ的取值必须非常大。然而,实际工程应用中为避免电容与变压器及其它负载发生谐振,在电容支路中串入了电感L,其感抗值为XL,取值通常为电容容抗的0.5%~12%[3-4]。由于电感L的存在,当晶闸管电流过零退出时,电容上的残压总会比系统电压峰值大,导致过零检测电路难以找到晶闸管两端电压的过零点而再次投入电容器。
传统的TSC控制电路中,晶闸管两端电压过零点检测由硬件完成,当控制信号关掉后,晶闸管会等待电流过零点自行关断,电流过零点正好是电压峰值点,由于电感L的存在,电容两端电压会比系统电压峰值高,只有靠电容内部的安全放电电阻将电容上的电压降至系统电压峰值附近,过零检测电路才能检测到电压过零点,补偿装置才能再次投入。由于电容内部的放电电阻数值很大,所以放电时间往往需要几分钟,当负载波动较大需要频繁投切时,补偿电容一旦切除,想要再次投入就必须等待过零条件,不能实现快速投入。目前在船舶制造行业、汽车制造行业中大量使用电焊机、缝焊机及点焊机等快速变化型负荷,传统TSC投切速度已经不能满足要求。
传统电路只能做到单纯依靠晶闸管两端的电压来判断投入点,因为无功补偿的电流相位超前系统电压相位90度,相对于电容电流来说这个投入点可能处于其稳态电流的较大值处,所以势必存在较长的暂态到稳态过渡时间,在暂态到稳态过渡时间内,电流非正弦波,如果容量较大,就可能会引起系统振荡。
2 带辅助支路的主电路
2.1 带放电辅助支路的主电路拓扑
为解决上述问题,使补偿装置能够适应系统无功需求变化快的情况,即能够在切除后瞬时再次投入电网,在电容器C两端加入由电阻R和晶闸管阀VT2构成的放电辅助支路。此时TSC单相电路模型如图2所示。

图2 带放电辅助支路的TSC单相电路模型
晶闸管阀VT2为放电晶闸管,其作用就是在主晶闸管VT1退出后,让电容器C通过R放电,使电容器C上的电压尽快放电至系统电压峰值或更低数值,从而使得主晶闸管VT1两端的电压能够有“过零点”,达到再次投入系统的条件。此时,主晶闸管VT1和放电晶闸管VT2的开通与关断的时机选择是此电路正常运行并达到预期效果的关键。
当主晶闸管VT1退出后,VT2将在控制器控制下开始工作;电容器C内部集成有放电电阻,并且控制器可以控制VT2的通断。当VT2闭合时,电容器C、晶闸管VT2和电阻R构成回路,使电容器C放电。因此,电容器C的电压处于下降状态,且从大于系统电压峰值Um的数值开始下降。UC为电容电压,Um为系统电压峰值。当UC>Um,且UC处于正向下降趋势,下降到接近Um时投入晶闸管,带放电辅助支路的单相电路工作过程如图3。在闭合主晶闸管VT1之前,放电晶闸管VT2处于闭合状态,此时电容电压UC大于系统电压Um,且其值从电容电压的最大值正向下降,在下降到系统峰值电压前切除放电晶闸管VT2的触发信号,此时VT2的电流经过一个过渡过程,到下一个系统电压过零点时,其电流过零使VT2关断;当系统电压U达到峰值Um时,电容C电流反向下降到接近零,闭合主晶闸管VT1后,在电源的作用下,电容充电,电容电压上升,由于电容残压大于系统电压,且此时刻电容电压与其稳态值非常接近,所以经过短时间的暂态后电容电压进入稳态;电容电流也反向增加并经过很短的暂态就可进入稳态,电流突变值小。然而若在UC<Um时触发主晶闸管VT1闭合,电容电压与稳态值相差数值较UC>Um时的大,所以要经过较长一段暂态后达到其稳态峰值。

图3 系统电压峰值时刻投入主晶闸管时单相电路工作过程波形
因此,UC>Um,且UC处于正向下降趋势时,系统电压达到峰值时投入主晶闸管VT1是最好的时机。主控制器通过对电容电压及系统电压的检测,可控制VT2的关断时刻,使得系统电压和电容残压满足此条件,此时可以实现投入电容时过渡过程最短,且冲击电流最小。
2.2 带充电辅助支路的主电路拓扑
要实现电容器放电至电压稍稍大于或接近系统电压峰值这个条件并不容易。原因在于在下次主晶闸管投入前,可能因为放电晶闸管不能关断而导致电容电压一直下降,而低于系统电压峰值;另外,即使放电晶闸管可以在电容放电至某电压时自行关断,电容自身也会因为内部的放电电阻以及自放电功能慢慢放电。所以必须用另外的方法实现电容两端电压的维持,既要使电容放电至接近系统电压峰值,又不至于一直向下降。只要电容两端电压能够维持住,后期系统无功需求变化时,就可以实现快速的补偿投入。因此,如何维持电容两端电压值接近系统电压峰值是快速投切的关键。
本文提出用外加辅助充电电路来实现电容两端电压的维持,其设计思路是:在主晶闸管两端外加可控的充电辅助支路,当主晶闸管退出后,将充电辅助支路接入到电源和补偿电容所在回路中去,用以维持电容上的电压不低于系统电压峰值。此充电辅助支路又可叫做二极管电压维持电路,如图4中主晶闸管VT1两端并接的电路。
图4所示电路在带有放电辅助支路的单相电路模型中,添加了一个由开关K1、电阻R1和二极管D1构成的“二极管充电辅助支路”。此电路利用二极管D1对电容C“充电”,用以维持电容C电压不低于系统电压峰值。当主晶闸管VT1退出后,放电晶闸管VT2闭合,此时将开关K1闭合,当电容C上的电压降至峰值以下,即电容电压小于系统电压时,就可以实现自动充电。在主晶闸管VT1退出后,电容C上电压高于系统电压峰值时,由于开关K1可以在主晶闸管退出后立刻闭合,即使此时没有充电电流,由于D1的存在,不会对整个电路带来不良影响;而在主晶闸管VT1再次投入时,会因为主晶闸管的零阻抗而将充电辅助支路“短路”,从整个电路拓扑里分离出去,与此同时可断开K1,切断充电支路,从而补偿装置正常投入到电网中。整个电路的目的是保证电容C两端的电压略高于系统电压峰值,且不会由于电容内部放电电阻或放电辅助支路作用而下降。要实现这个电路的安全运行,必须要使主晶闸管VT1在系统电压正半波时关断,且当电容C放电至稍大于系统电压峰值时,使放电晶闸管VT2关断,断开放电支路。
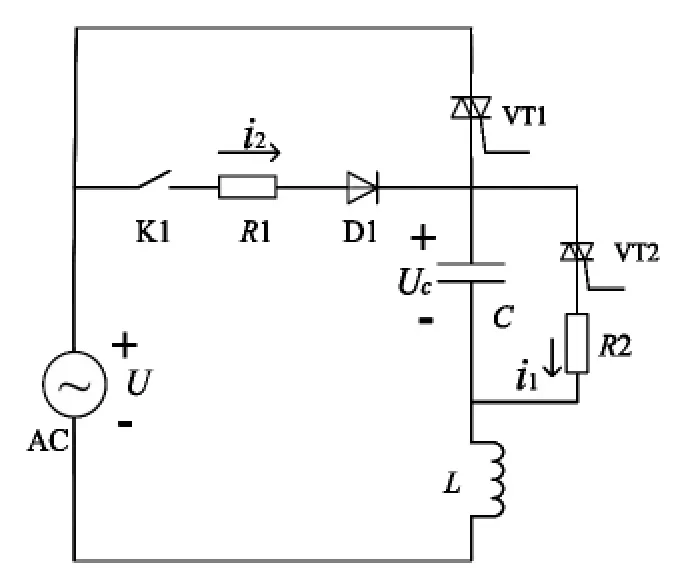
图4 带有充电和放电辅助支路的单相电路模型
2.3 基于全控器件的直流电压维持法
为了能够可靠地断开放电支路,可将放电晶闸管VT2替换为全控型器件如IGBT,并且把二极管充电电路中的开关K1也替换为全控型器件。放电辅助电路和充电辅助电路都使用全控型器件,构成了“电压维持电路”,这种电路能更精确地维持电容电压处于略大于系统电压峰值,从而让补偿系统时刻处于“热备投”状态,主控制器能随时根据系统无功变化需求而投入和切除补偿装置,从而达到真正的快速无冲击投切。这种依靠维持电容两端电压恒定为略大于系统电压峰值的方法即直流电压维持法,它是实现无功补偿系统快速投切的关键。
使用全控型器件后,带有电压维持电路的单相电路模型如图5所示。图中由R1、D1、VG1构成充电辅助支路,由R2、D2、VG2构成了放电辅助支路。为了防止主晶闸管VT1投入后,在系统电压负半波时,VG2内部的反并联二极管会提供一个电流通道,导致放电电阻R2上的功率很大而烧坏,在放电辅助支路中,加入了二极管D2。
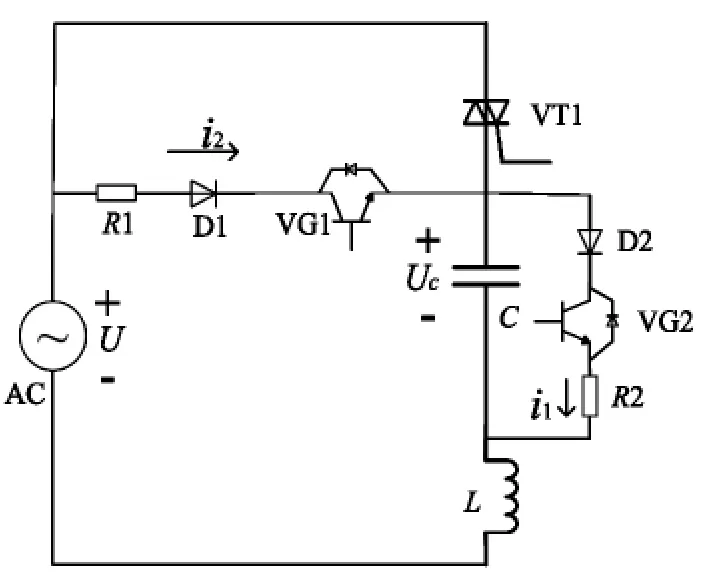
图5 带有电压维持电路的单相电路模型
在此单相电路模型中,放电电阻R1和充电电阻R2阻值可以用补偿电容电压的变化产生的电流平均值进行估算。以R1为例,忽略D1、VG1上的压降,假设t时间内,要使补偿电容电压增加ΔU,则流过R1的电流i2值为:

实际电流按指数工程计算方法,取电流的二分之一作为平均值,则R1值可估算为:

在工程应用中,主控制器可利用采样电路得到补偿电容电压及系统电压值,采用滞环控制的方法选择VG1及VG2的投切时机,具体投切区间可参考图6。纵轴即主电容器C上直流电压,横轴表示主晶闸管以及辅助全控器件投入的角度,图中虚线即投入或退出的区间。当主电容器C初次投入,即其电压绝对值小于200 V时,需要在第一次到达主晶闸管VT1退出区间,即系统电压相位位于20°到70°之间时退出主晶闸管VT1,此后主电容器C的电压通过放电辅助电路及充电辅助电路能够维持在系统电压正峰值上,进入热备投状态。
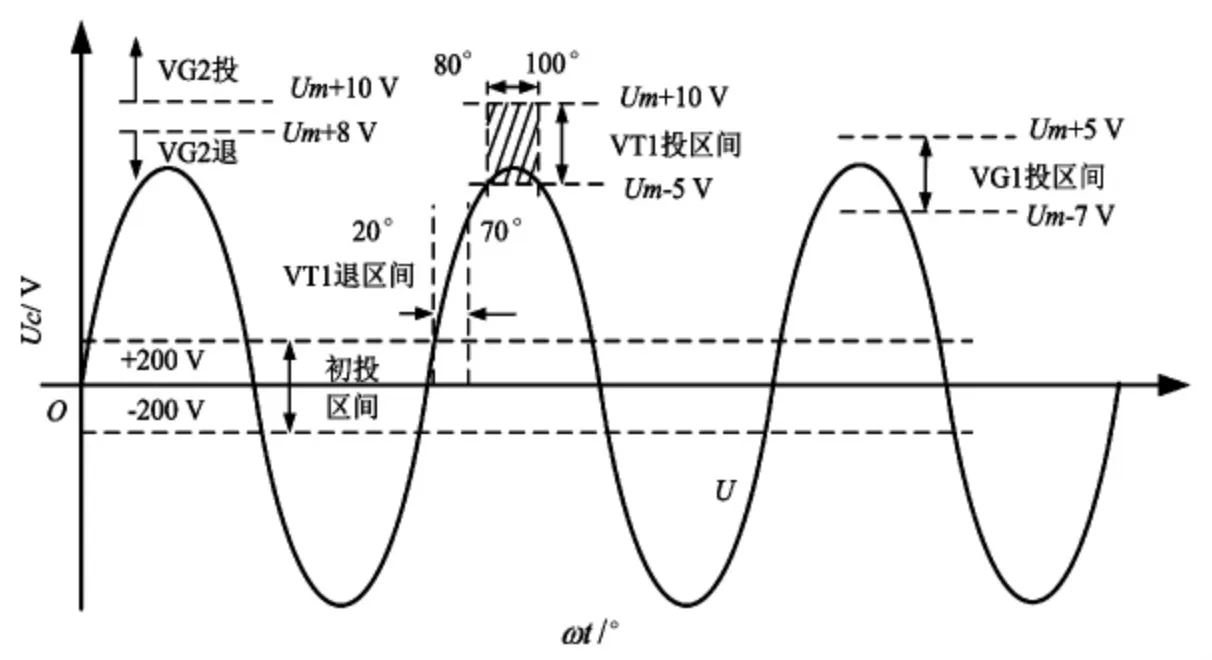
图6 主晶闸管和辅助全控器件的投切区间
3 仿真电路及结果
用Simulink搭建单相电路模型如图7所示。图7中VT1和VT2两个反并联晶闸管作为主晶闸管,用晶闸管驱动信号控制其通断。两个晶闸管控制信号相同,但同一时间只有一个导通。VG1和VG2分别是充电辅助支路及放电辅助支路的开关,其中ChargeSwitch可以控制整个仿真是否要加入充电辅助支路,而DischargeSwitch开关则用来控制是否加入放电辅助支路。开关SW控制负载通断。
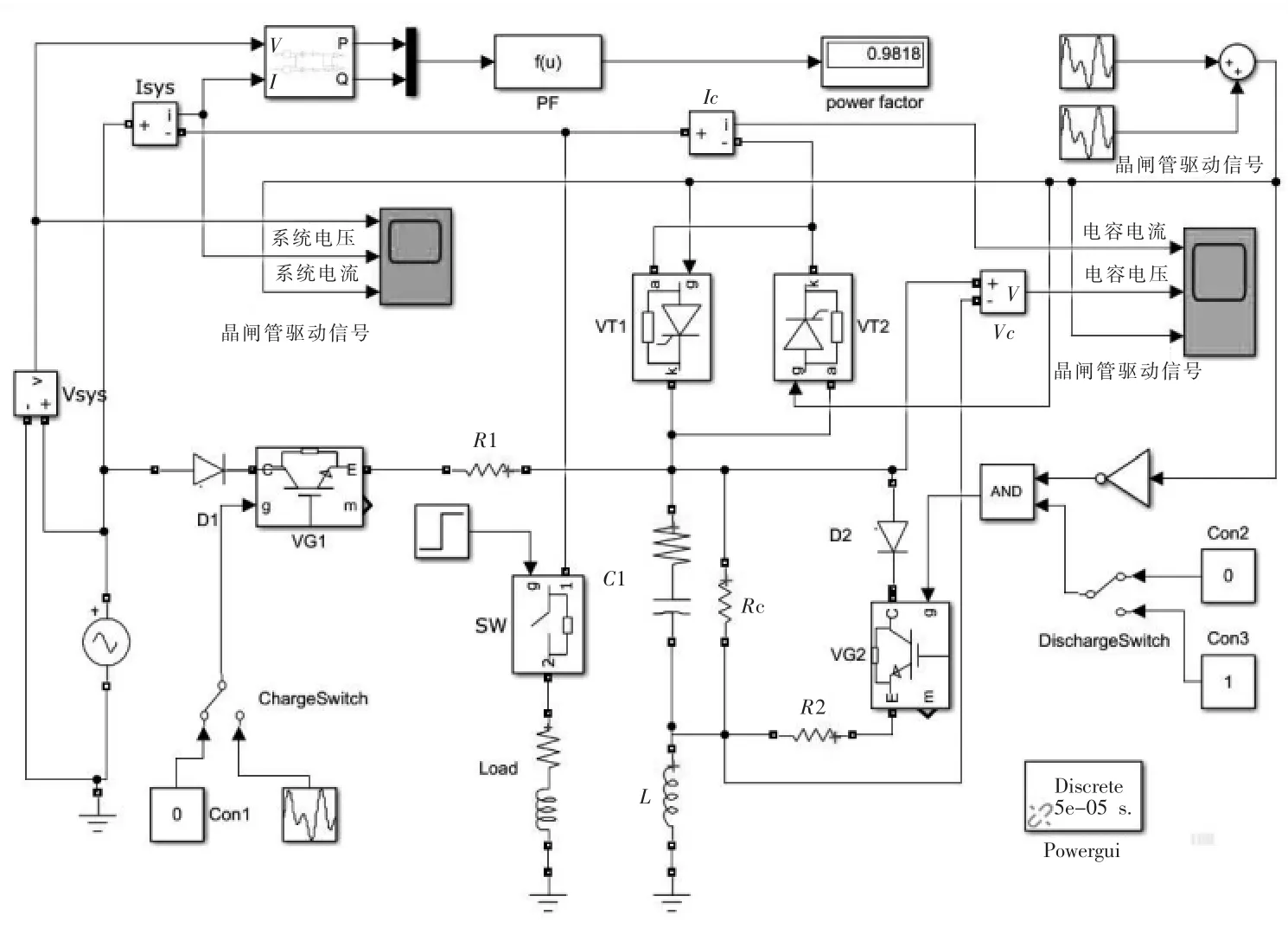
图7 基于直流电压维持法的单相电路仿真模型
仿真电路参数如下:系统电源为380 V,频率为50 Hz;感性负载有功功率为20 kW,无功功率27 kvar,功率因数约为0.6;补偿电容500 uF。其工作过程是:开关SW在0.1 s时接通,此时负载接入电路,0.2 s时给晶闸管驱动信号,此时投入补偿电容;在0.222 s时断开晶闸管驱动信号,接下来0.245 s时再次投入补偿电容。用此方法模拟补偿装置的快速投切的同时,利用ChargeSwitch和DischargeSwitch控制两个开关通断,对带有辅助支路的主电路和传统主电路分别进行仿真,对比投切补偿电容时充击电流的情况,得到的波形如图8、图9所示。
补偿装置断开后再次投入的时间点选取为紧接着第二个系统周期的系统电压峰值时刻,此时电容电压略大于系统电压峰值。断开ChargeSwitch和DischargeSwitch两个开关,用示波器观测波形。传统主电路系统电压、系统电流及晶闸管驱动信号、补偿电容电压、补偿电容电流及晶闸管驱动信号的波形如图8所示。此时未加入充电辅助支路和放电辅助支路。从图8看出,当补偿装置切除后再次投入时,虽然系统电压和电流相位差几乎为零,补偿电容起到补偿作用,但是投入时产生接近200 A的冲击电流,是稳态电流峰值的2倍;在补偿电容第二次投入时,电容的冲击电流达到100 A,并产生了短时间的振荡。

图8 传统主电路系统电压、系统电流、补偿电容电压、补偿电容电流及晶闸管驱动信号波形
接通ChargeSwitch和DischargeSwitch两个开关,即加入充电辅助支路和放电辅助支路,仿真得到的系统电压、系统电流、补偿电容电压、补偿电容电流及晶闸管驱动信号波形如图9所示。由图可以看出快速投切时系统充击电流几乎为零,电容电流的过渡过程很短,整个系统很快进入稳态。

图9 基于直流电压维持法电路的系统电压、系统电流、补偿电容电压、补偿电容电流及晶闸管驱动信号波形
4 结语
本文在传统主电路拓扑中添加包含有源器件的辅助电路支路,通过控制有源器件的通断,使补偿电容上的电压维持在系统电压峰值附近,为快速投入电网创造条件,使补偿系统时刻处于“热备投”状态,从而能使补偿电容分离后快速投入电网。从仿真分析可看出此主电路拓扑能够实现补偿电容从电网切除后,在下一个系统周期内再次投入电网使用,真正实现了快速投入,且有效抑制了传统投切电路中补偿电容投入时产生的冲击电流。这种拓扑结构能够为大量使用电焊机、缝焊机及点焊机等快速变化型负荷的应用场合提供解决方案。
