非全周开口滑阀的流场特性及其优化*

2022-03-23宋子龙张晓俊梁义维

机电工程 2022年3期

宋子龙,张晓俊,梁义维,张杰

(太原理工大学机械与运载工程学院,山西太原 030024)

0 引言

滑阀是液压控制系统中的重要组成部分,而其中的阀芯位移改变流体的流向及阀口的开度,其性能对整个液压系统关系重大。

液动力是影响滑阀性能的重要因素之一[1]。当流体流经液压阀的阀口时,其流速和方向会发生变化,从而导致流体的动量发生变化,进而对阀芯产生一个轴向力(即液动力),过大的液动力会影响液压阀的操纵力及稳定性,从而对整个液压系统的性能产生影响[2]。

许多学者采用计算流体力学(CFD)对滑阀内部流场的特性及其液动力进行了研究[3-5]。张晓俊[6]采用对滑阀阀芯壁面压力分布的表面积进行积分的方式,研究了滑阀的稳态液动力。AMIRANTE R等人[9]提出了一种减小比例阀的液动力,并保证其所需阀口开启力不变的方法。AMIRANTE R等人[10]分析了流量对滑阀液动力的影响,并对此进行了试验,以验证仿真分析的结果。廖瑶瑶等人[11]建立了液压支架用换向阀流道模型,并提出了解决换向阀复杂流道液动力的方法。汤志勇等人[12]提出了一种滑阀的阀芯固定,而其阀套运动的方法,并将其用于对滑阀的稳态液动力进行补偿。白琼[13]对型槽、V型槽、K型槽和全周开口的水液压滑阀稳态液动力进行了计算,得出了全周开口液动力最小,V型槽液动力最大的结论。袁俊等人[14]利用动网格分析了电液伺服阀二维模型在不同时刻的受力情况,为滑阀的设计提供了参考。BURECEK A等人[15]通过试验测量和数学模拟的方式,对比例阀的液动力、压力和阀芯位置的关系进行了研究。

上述研究人员对滑阀[16]所进行的研究多数着眼于稳态液动力。然而在大流量、小开口、阀芯高速运动时,滑阀的瞬态液动力也会较大。因此,在上述研究中,研究人员普遍都忽略了阀口气穴现象对滑阀液动力的影响,导致在滑阀开口度较小时,其压力值与实际压力不符。

以非全周开口滑阀为研究对象,笔者采用两相流模型对其内部流场进行分析,通过仿真计算得出滑阀稳态液动力和瞬态液动力,进行具体分析,并通过液动力对阀套结构进行优化,为液压阀的设计提供理论依据。

1 网格模型及其计算

1.1 几何模型

非全周开口内流式滑阀结构示意图如图1所示。

图1 非全周开口内流式滑阀结构示意图

图1中,滑阀由阀体、阀套和阀芯组成,阀套入口处加工4个方形孔进行节流,出口处为4个圆形孔,不产生节流作用。

x为阀芯运动过程中所研究的阀的开口值,其主要尺寸为:a=18 mm,b=10 mm,c=d=6.5 mm,e=3 mm,f=6.5 mm,D=12 mm,m=18 mm。

1.2 网格划分

由于滑阀内部流道比较复杂,笔者采用SolidWorks软件和Geometry软件建立滑阀流体域三维模型,如图2所示。

图2 滑阀流体域三维模型

由于滑阀三维模型的结构具有对称性,为了减小计算量和提高计算精度,可取其半剖模型进行研究。

笔者使用前处理软件ICEM CFD进行网格划分。为了便于计算收敛,大部分区域采用六面体网格,部分区域采用四面体网格;考虑到阀口附近压力和速度梯度较大,故进行细化处理。

同时,笔者对不同数量的网格进行无关化检验,即分别选取38 128、62 452和106 575的网格数量进行检验,结果发现其对计算的结果没有影响。

流体域半剖网格模型如图3所示。

图3 流体域半剖网格模型

1.3 计算条件

笔者采用速度入口和压力出口进行仿真计算,并且通过给定进口速度来控制流量的大小。半剖截面设为对称面,其余与流体接触壁面为静止壁面;流体设为牛顿流体,不可压缩,流动状态为紊流,采用标准k-ε模型;流体介质选为液压油,密度为850 kg/m3,运动黏度为0.02 kg/m·s,出口压力为0.12 MPa。计算模型和计算条件与实际工况相对应。仿真过程中选择适当的欠松弛因子,保证计算收敛,从而得到准确合理的解。

考虑到实际情况中的气穴现象,笔者在Fluent中的多相流模型里选择气穴模型,采用气穴模型进行计算可以模拟流场里的气泡在压降下形成气穴。研究中运用Fluent中的动网格技术来模拟阀芯移动的过程,采用动态层技术计算,运动区域设置为刚体运动。

当阀芯的运动速度为0.5 m/s时,阀芯运动不同位置的网格示意图如图4所示。

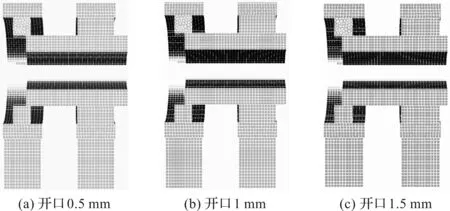
图4 阀芯运动不同位置网格示意图

2 仿真计算及分析

2.1 压力场和速度场

阀芯运动使阀口打开时,不同流量和阀口开度的滑阀稳态流场压力云图和速度云图,如图5所示。

当阀芯的运动速度为0.1 m/s时,滑阀的瞬态流场压力云图和速度云图如图6所示。

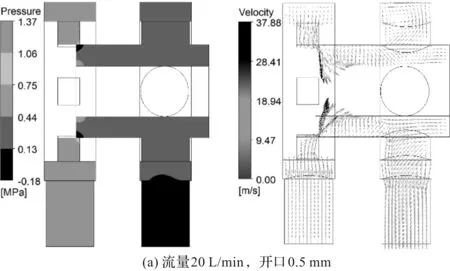
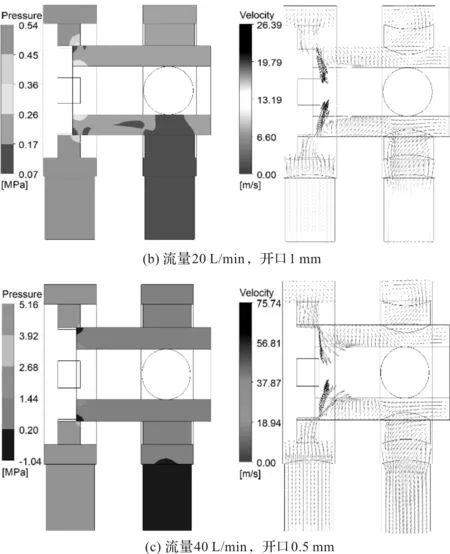
图5 滑阀稳态流场压力云图和速度云图

图6 滑阀瞬态流场压力云图和速度云图

由图5和图6可知:

油液流经阀口时会产生压降,这种现象在低压区域也比较明显;当油液刚进入阀内时,其速度基本稳定;当油液经过阀口时,由于过流面积突然减小,其流速增大,由伯努利方程可知,阀口处的压力减小;相同开口和流量情况下,瞬态流场的压降和射流速度明显小于稳态流场;

随着阀口开度的增大,阀口处的低压区域明显减小,阀口处前后压差变小,压力损失减少,最大压力减小,最小压力升高,阀内整体压力分布改变,因此阀口开度可以改变阀内压力分布情况。随着开口度的增大,油液流经阀口的通流面积增大,阀口的节流作用减弱,压力升高,阀口处的射流速度减小,入口射流角减小;

当阀口的开度一定时,流量越大,滑阀流场的最大压力和阀口处的压力差都会变大,压力损失也会增加。因为压力变大,所以液流经过阀口时的射流速度明显增大,同时射流角变小。

2.2 两相流仿真分析

由于油液流经阀口时的射流速度较大,会产生油液和壁面分离的现象,主流的油液会带动壁面附近的油液以一定的能量流动,然后回流。主流的油液动能很大,回流的油液会因回流不充分使流场产生低压区域,区域内的绝对压力比油液和空气的分离压力小,因此,油液中有气泡产生,也即出现气穴现象。

流量为60 L/min,阀口开度为0.5 mm时的气相体积分数云图如图7所示。

图7 气相体积分数云图

2.3 液动力

液动力是因为油液流经阀口时流速和方向发生变化,引起油液的动量发生变化,从而使阀芯受到的一种附加作用力。通常,液动力可以采用动量定理来计算。

根据动量定理,可得滑阀的稳态液动力为:

FS=ρqv1cosθ1-ρqv2cosθ2

(1)

通常认为流体出口射流角θ2为90°,因此,此处的液动力公式可写为:

FS=ρqv1cosθ1=2CqCvSΔpcosθ1

(2)

式中:Cq—流量系数;Cv—流速系数;Δp—进出口压差;S—节流口过流面积;θ1—入口射流角,最理想为69°。

滑阀的瞬态液动力动量公式为:

(3)

采用CFD仿真计算得到的稳态液动力,实际就是在阀芯静止时,对阀芯两壁面压力的面积进行积分得到的差值。而瞬态液动力则是在阀芯运动状态下,对阀芯两壁面压力的面积进行积分得到的差值。

不同流量下,随着阀口开度变化的稳态液动力的仿真曲线如图8所示。

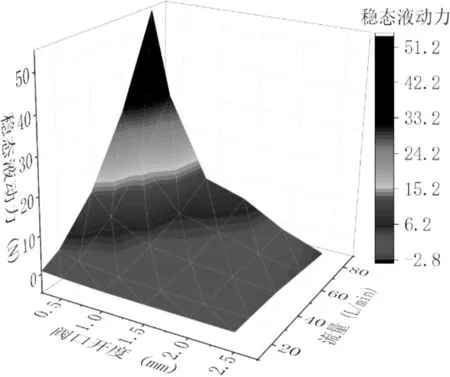
图8 稳态液动力仿真曲线正值—液动力指向阀口关闭方向;负值—液动力指向阀口打开方向

由图8可知:在阀口开度一定时,稳态液动力随着流量的增大而变大。因为流量增大会使进口处液流流速和进出口压差增大,所以由式(2)可知,其稳态液动力也随之增大;

在流量一定时,阀口开度增大会导致进出口压差减小,进而稳态液动力也减小。阀口开度在0～1 mm时,稳态液动力较大,减小的幅度也较为明显。因此,在阀口开度微小的时候,稳态液动力的变化比较大;在阀口开度为1 mm～2.5 mm时,稳态液动力较小,减小幅度比较缓慢;

在阀口开度不断增大的过程中:当开口在0～2 mm内时,稳态液动力虽然一直在减小,但始终为正值,即液动力方向为趋于阀口关闭方向;当阀口开度在2 mm～2.5 mm时,稳态液动力继续减小,直到其值变为负值,即液动力方向为趋于阀口打开方向。这是因为随着阀口开度的增大,阀口处的前后压差减小,入口处的射流速度和射流角减小,当其开口达到一定程度时,射流角接近90°,因此,由式(1)可知,液动力会出现负值。

随着阀口开度的变化,不同的流量和阀芯运动速度的瞬态液动力仿真曲线,如图9所示。

图9 瞬态液动力仿真曲线

从图9中可知:

影响滑阀瞬态液动力的主要因素有阀口开度、阀芯速度以及流量;和稳态液动力一样,瞬态液动力与滑阀的阀口开度成反比(即随着开口度的增大,瞬态液动力减小);在阀口开度和阀芯移动速度不变时,瞬态液动力随着流量的增大而变大;当流量一定时,阀芯运动速度越快,瞬态液动力就越大。

对比瞬态液动力和稳态液动力的仿真曲线图可知:

在相同条件下,滑阀稳态液动力比瞬态液动力大很多;由式(1,2)可知,稳态液动力和瞬态液动力都与阀口处的压差有关;

由图(8,9)可看出:瞬态流场阀口处的压差明显小于稳态流场,因此瞬态液动力比稳态液动力小。但是,在阀芯运动速度很快、流量较大,并且阀口开度很小时,其瞬态液动力也会比较大,不可以忽略不计。因此,在对滑阀进行研究和设计时,瞬态液动力也要加以重视。

3 阀套结构优化及分析

液动力是影响液压阀性能的因素之一,它不仅影响阀的驱动力,也会使阀产生自激振动,降低阀的操纵稳定性,对整个液压系统的稳定性造成影响,甚至会降低阀的使用寿命。因此,对滑阀的液动力进行优化补偿研究具有重要的意义。

笔者提出一种针对滑阀阀套结构的液动力优化方案,即将阀套进油孔处的4个方孔设计为斜孔,油液进入阀套的方向为倾向于阀口打开的方向,倾斜角为θ。

θ=20°时的阀套半剖模型,如图10所示。

图10 θ=20°阀套半剖模型

当倾斜角为θ=10°、θ=20°和θ=30°时,笔者分别建立滑阀的三维模型,并在同等条件(优化前)下,对其进行仿真计算。

θ=20°和θ=0°(优化前),阀芯开启时的液动力仿真曲线,如图11所示。

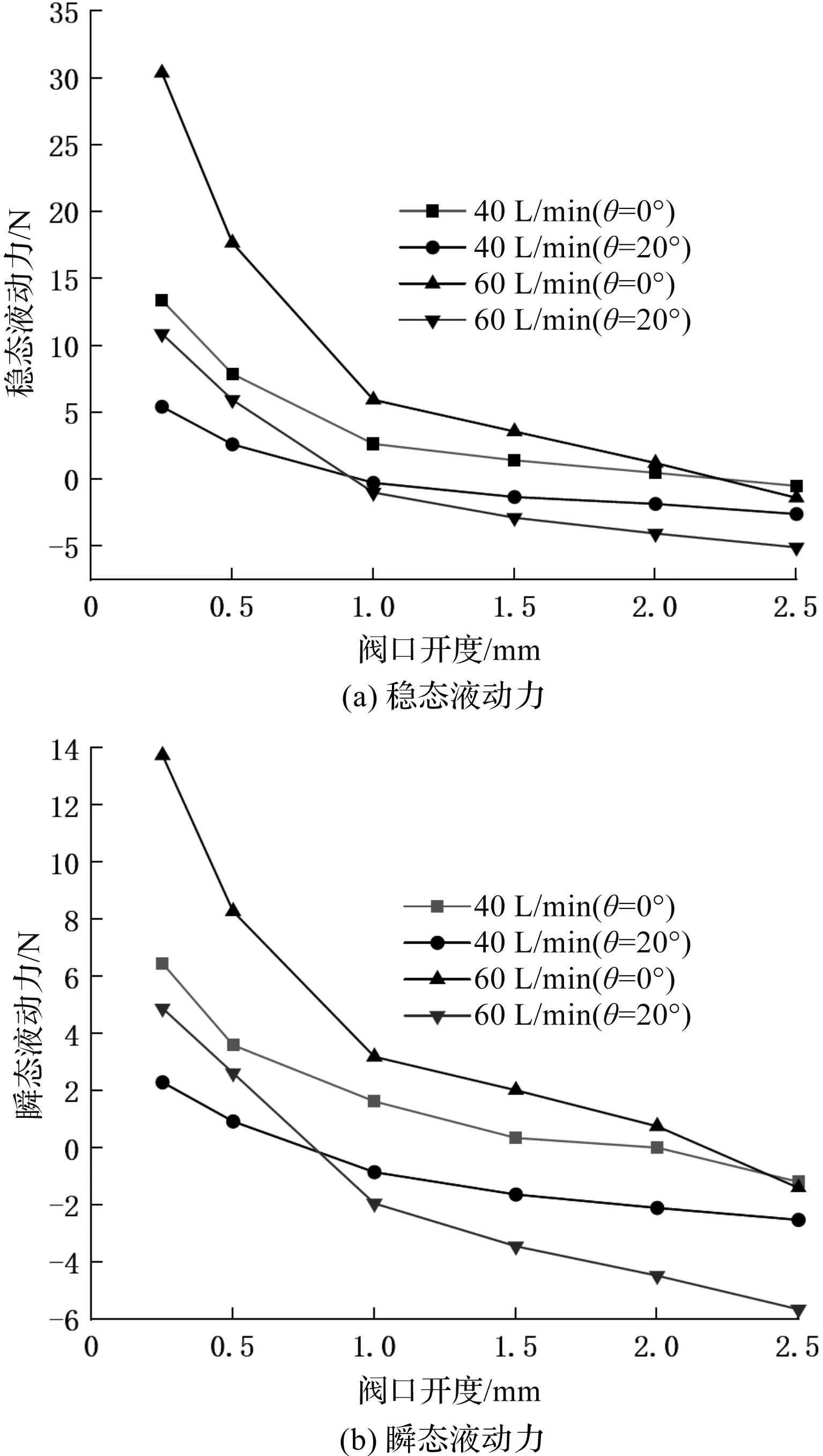
图11 优化前后液动力仿真曲线

由图11可知:

(1)将阀套进油孔设计为斜孔后,可以有效降低滑阀的液动力,且流量越大,优化效果越明显;

(2)优化前后液动力仿真曲线的斜率很相似,都是在阀口开度达到1 mm之前,液动力减小较快,在1 mm之后变得缓慢。

不同之处在于,优化前的液动力随着开口增大而减小,方向为趋于阀口关闭方向,在开口2.2 mm时接近零点,液动力变为负值,方向趋于阀口打开,且随着开度的增大而变大;在开度达到1 mm时,优化后的稳态液动力接近于0;在阀口开度0.8 mm时,瞬态液动力接近于0。这是因为优化后阀套的倾斜方向为阀口打开方向,因此进油方向也倾向于阀口打开方向,相较于优化前,壁面1受到的力更大,优化后的瞬态液动力和稳态液动力绝对值明显减小。

当流量为60 L/min,阀芯以0.1 m/s的速度打开阀口时,不同倾斜角的滑阀液动力仿真曲线如图12所示。