不同受损情况下珊瑚礁海岸动力地貌差异性分析

2022-03-23陈燕珊戚洪帅杨清书蔡锋刘根朱君赵绍华

海洋学报 2022年3期

陈燕珊，戚洪帅，杨清书，蔡锋，刘根,5，朱君，赵绍华

(1.中山大学海洋工程与技术学院中山大学河口海岸研究所，广东广州 510275；2.自然资源部第三海洋研究所海洋与海岸地质研究室，福建厦门 361005；3.河口水利技术国家地方联合工程实验室，广东广州 510275；4.广东省海岸与岛礁工程技术研究中心，广东珠海 510275；5.自然资源部北部湾滨海湿地生态系统野外科学观测研究站，广西北海 536015)

1 引言

在全球气候变化和人类活动频繁背景下，珊瑚礁海岸最常见的地貌组合——珊瑚礁–海滩系统对环境变化响应极其敏感，探索珊瑚礁与海滩地貌之间的动力地貌联系是认识珊瑚礁海岸变化的重要一环，可为海岸防护和生态修复提供科学依据。

波浪过程是珊瑚礁海岸研究中的重要科学问题，礁体能有效削弱外海传至近岸波能，对岸滩起到一定保护作用[1]，目前多数研究集中于对影响礁体波浪传播过程的因素进行分析。研究表明，礁坪水深、礁坪宽度、岸滩坡度、礁体形态通过影响波浪传播变化如波浪破碎、摩阻损失、礁坪共振等过程，引起不同频段波能的重新分配，导致近岸波能主控频段分布呈现差异性特征[2–8]。不同地貌对动力、沉积输运过程差异导致海滩地貌特征不同，尽管前人有所研究[7,9–14]，但针对珊瑚礁海岸区域，近岸不同主控频段波浪影响下的海滩地貌特征分析研究存在不足，因此，有必要开展珊瑚礁海岸对区域波浪能量变化以及礁后海滩地貌的研究，探讨礁体地形与礁后海滩动力地貌之间的联系。数值模型是研究珊瑚礁海岸波浪过程常用的方法之一，相位平均模型如SWAN、Delft-3D、MIKE21 SW 等模型对波浪过程的求解一般基于能量守恒原理，但此类模型无法精细刻画珊瑚礁海岸波浪传播过程。相位解析模型如非静压模型、Boussinesq类模型可模拟高色散完全非线性波浪过程，计算精度和效率相对更高。基于激波捕捉的完全非线性Boussinesq方程模型FUNWAVE 可避免因引入人工率定经验参数带来的不确定性，被成功应用于珊瑚礁海岸波浪传播的模拟[4,15]。本文通过对华南雷州半岛徐闻西落港珊瑚礁海岸沉积以及地形特征分析，运用FUNWAVETVD 模拟分析不同礁体地形上波能传播过程，并结合礁后海滩平衡剖面特征，探讨珊瑚礁海岸礁后海滩动力地貌差异性及其机理。

2 材料和方法

2.1 野外调查

研究区为徐闻西落港珊瑚礁海岸，地处广东雷州半岛西南海岸、灯楼角北部区域，与海南岛北部隔海相望（图1a），是我国珊瑚礁海岸（岸礁）的主要分布区域之一，该区域珊瑚礁因受到如炸鱼、礁坪采掘、养殖引起水质污染等人为活动的影响而发生一定损毁以及退化[16]。该海区为热带季风气候，属全日潮，潮差约为1.5 m，波浪主要由外海传入，具有明显季节性变化，波高约为0.6 m[17]。

为了研究其地形地貌特征，对该区域开展了野外调查。调查断面根据历史资料选择礁坪存在明显差异的剖面进行布设，剖面调查时间是在2020 年8 月10–11 日（夏季），该处主要受夏季西南向浪影响，调查时间可以适当反映海滩状态。研究区域从南向北布设P1、P2 和P3 3 个珊瑚礁海岸剖面（图1b），3 个剖面礁体受损程度不同，P2 剖面海滩上珊瑚礁碎屑数量较多且颗粒较大，其次是P3 剖面，而P1 剖面海滩上珊瑚礁碎屑相对更少（图1c 至图1e）。岸滩地形测量采用STONEX S9Ⅱ型的RTK-GPS，水平和高程误差分别为±1 cm 和±2 cm，从后方植被线向海测至涉水深度（图1c 至图1e 虚线）。水下地形测量采用云洲SE40 型的无人船搭载单波束完成，测量范围水深0.5～10 m（图1b 虚线）水平误差和水深精度分别为±10 cm 和±5 cm。研究区海滩沉积物差异不大，选择P1 剖面进行表层沉积物采样，采样高程间距为0.5 m，共获得10 个表层沉积物样品。

图1 研究区域Fig.1 Study area

2.2 沉积物粒度分析

沉积物粒度分析采用激光粒度分析法和筛分法相结合的方式，对于相对较粗的沉积物样品（含砾石），取适量烘干，加入去离子水充分分散，使用筛分法对粒度大于2 mm 的颗粒进行粒度分级。而对于其中粒度小于2 mm 的部分沉积物，取适量样品溶液，加入0.05 mol/L 六偏硫酸钠溶液约5 mL，使用马尔文公司生产的MS2000激光粒度仪（0.02～2 000 μm）进行粒度分析。粒度参数计算采用福克–沃德粒度参数公式[18]，粒级标准采用尤登–温德华等比制Φ 值粒级标准[19]，沉积物类型采用谢帕德的沉积物粒度三角图解法[20]。

2.3 数值模拟与验证

数值模型采用基于完全非线性Boussinesq 方程的FUNWAVE-TVD 3.5 模型，该模型适用于模拟近岸波浪浅化、反射、折射、破碎以及波浪在岸滩区域的爬高与下冲等过程[21]。模拟区域徐闻剖面总长为2 000 m，礁体底床摩擦系数Cd=0.05，入射波谱型采用研究中常用的JONSWAP 不规则波经验谱，谱峰升高因子γ=3.3，在礁缘外入射。徐闻月平均波高为0.6 m，月平均波周期为3.5～4.9 s[16–17,22]，故正常波况波浪设置为谱峰周期Tp=4.6 s，入射波高Hi=0.6 m。采样频率为1.0 s，模拟时长以水位时间序列达到稳定状态并持续一段时间为止。模型区域设置如图2。模型输出水位时间序列最后相对稳定的200 s 的数据用于谱分析，谱分析参数设置取默认值，采用Hanning 窗口，50%重叠率，频域分辨率为0.009 8 Hz。短波频率一般介于0.04～1.00 Hz之间，次重力波指频率低于短波的海表面流体波动，频率一般介于0.005～0.04 Hz 之间。由水位时间序列的谱分析可得波能密度–频率（S（f）-f）分布关系，进而可计算全谱波波能（式（1））、短波波能（式（2））以及次重力波波能（式（3））（f为频率，单位为Hz）。

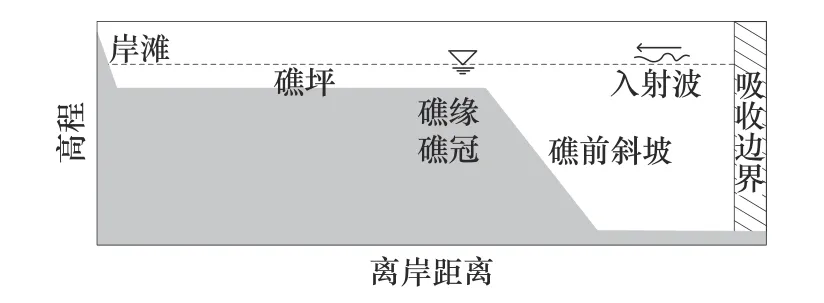
图2 珊瑚礁海岸剖面数值模型区域设置示意Fig.2 Schematic of cross-shore profiles of reef topography in the numerical experiments

为对FUNWAVE-TVD 数值模型模拟珊瑚礁海岸波浪传播过程的适用性进行验证，本文将模型模拟结果与密歇根大学进行的基于概化珊瑚礁地形的水槽模型实验[23]结果进行误差分析（式（4）[24]，图3），结果表明数值模型结果与水槽模型结果吻合较好，有效波高模拟误差Skill≈0.93，次重力波波高模拟误差Skill≈0.79，故该数值模型模拟精确度较高，适用于珊瑚礁海岸波浪过程的模拟。在对模型进行验证后，接下来对模型数值稳定性进行探究：数值稳定性与模型使用网格大小有关，一般以波长作为网格大小选取的参考依据。本文数值模型以2 倍关系加密计算网格，计算区域网格大小ρΔx分别为Lp/21、Lp/41、Lp/82、Lp/165（Lp为谱峰波长），选取离岸50 m、100 m 处波面变化稳定性进行了分析（图4），可知模型在Δx=Lp/165，即单位网格大小约为0.2 m 时，结果已收敛。

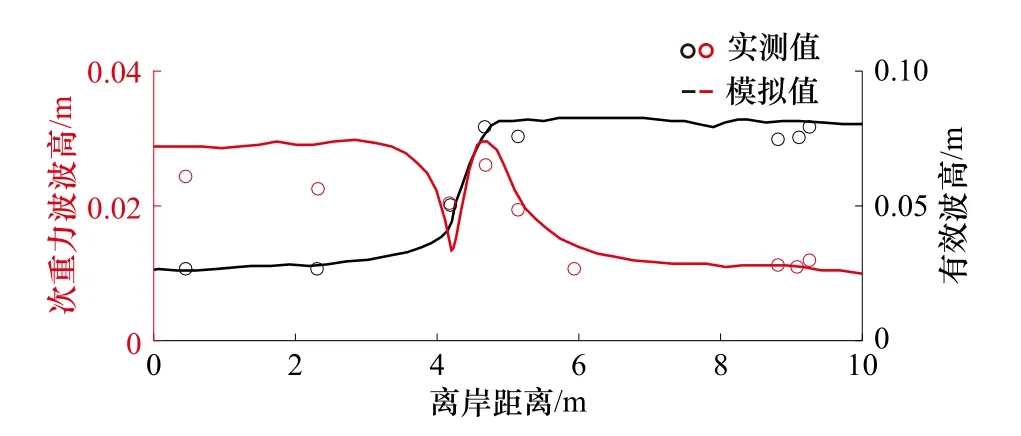
图3 有效波高（黑线）和次重力波波高（红线）实测值与数值模拟值比较Fig.3 Spatial variations of measured and predicted significant wave heights (black line),infragravity wave heights (red line)

图4 网格尺寸对剖面离岸50 m 和100 m 处波面变化的影响Fig.4 Influence of grid sizes on water surface elevation at 50 m and 100 m distance from shoreline

式中，N是实验点总数；Xp是模型模拟值；Xo是实测值；Skill值越接近1，表明误差越小。

3 结果

3.1 珊瑚礁海岸地形地貌与沉积特征

徐闻西落港珊瑚礁海岸P1、P2、P3 3 个剖面礁坪基本淹没于平均海平面之下，且主要分布于潮下带，3 个剖面珊瑚礁和礁后海滩地貌呈现明显差异性特征。P1 剖面珊瑚礁发育较完善，礁坪宽度是3 条剖面中最宽广的，礁缘水深为1.27 m，礁后海滩宽度小而坡度大，后滨无滩肩发育，整体处于稳定状态；P2 剖面珊瑚礁受破坏较严重，礁坪窄短，礁缘水深为0.69 m，礁后海滩较宽缓，处于侵蚀状态；P3 剖面活体珊瑚覆盖率高，礁坪宽度较P1 小，但礁缘水深较大，礁后海滩滩肩发育，海滩坡度与P1 近似，稳定性较好（图5，表1）。比较来看，P1 和P3 剖面海滩的反射性较强，而P2 剖面滩面耗散性较强[24]。

图5 徐闻西落港珊瑚礁海岸地形Fig.5 Topography of fringing reef in Xiluo Port,Xuwen

表1 徐闻西落港珊瑚礁海岸不同剖面地形参数Table 1 Topographic parameters of fringing reef in the Xiluo Port,Xuwen

海滩表层沉积物类型以砂为主，中值粒径在0.24 Φ～1.95 Φ 范围内变动，由岸向海，表层沉积物粒径逐渐变细，平均高潮面和平均海平面间的区域岸滩表层沉积物粒径变动较大，平均海平面以下，表层沉积物粒径基本不变（图6）。

图6 徐闻西落港海岸P1 剖面粒度参数沿程分布Fig.6 Cross-shore distribution of surface sediment grain-size parameters in the Xiluo Port,Xuwen

3.2 不同剖面的波能差异

基于实测剖面地形，对3 个不同特征的珊瑚礁海岸进行数值试验。模拟结果表明，受岸滩差异性反射作用影响，各剖面礁后海滩附近波浪呈不同程度振荡趋势分布，研究区不同剖面礁后海滩（0 m 等深线）短波波能Ess0、次重力波波能Eig0、短波波能占全谱波波能比重（Ess0/E0）、次重力波波能占全谱波波能比重（Eig0/E0）、短波波能相对入射短波波能变化率（(Ess0−Essλ)/Essλ）、次重力波波能相对入射次重力波波能变化率（(Eig0−Eigλ)/Eigλ）均呈现明显差异性特征（图7，表2）。

图7 徐闻西落港珊瑚礁海岸短波波能（Ess0）（a1−a3），次重力波波能（Eig0）（b1−b3）和珊瑚礁海岸地形（c1−c3）沿程分布Fig.7 Spatial variations of short wave energy (Ess0) (a1−a3),infragravity wave energy (Eig0) (b1−b3) and reef topography (c1−c3) in the Xiluo Port,Xuwen

表2 徐闻西落港珊瑚礁海岸0 m 等深线处波能及波能成分比重Table 2 Wave energy and its’ variation in different wave band along the 0 m isobaths in the Xiluo Port,Xuwen

各剖面礁后海滩短波相对外海都是衰减的，P2剖面近岸短波波能相对外海短波波能衰减率最大，短波波能最小；P1 剖面近岸短波波能衰减率略小于P2 剖面；P3 剖面短波波能衰减率最小，到达礁后海滩短波剩余波能最大。各剖面礁后海滩次重力波波能相对外海都显著增大，其中P3 剖面次重力波波能增长率最大，P1 剖面次重力波波能增长率最小。由于各剖面短波波能和次重力波波能变化率不同，礁后海滩各频段波能占全谱波波能比重出现差异。P1 和P3 剖面礁后海滩短波波能占全谱波波能比重都大于对应剖面次重力波波能占全谱波波能比重，其中次重力波波能占全谱波波能比例分别约为30.42%和43.86%；P2 剖面则与之不同，礁后海滩次重力波波能占全谱波波能的86.89%。总体来看，耗散性强的P2 剖面礁后海滩波能以次重力波频段波浪为主，而对于反射性较强的P1 和P3 剖面礁后海滩波能主要以短波波浪为主。

4 讨论

4.1 剖面波能差异性原因分析

研究区各剖面波能沿程变化规律基本与前人研究结果一致[25–27]，模型试验可以较好的体现其波浪过程差异。不同剖面波能分布呈现明显差异，因波浪传播过程受礁体水深、礁坪宽度、地形坡度等因素影响显著。

波浪由外海传播至近岸时，波浪在礁缘附近发生破碎，波浪破碎引起水体强烈的紊动和漩涡，导致入射短波波能显著衰减。在波浪继续向岸传播过程中，礁坪水深越小，因礁坪底床对波浪水流的摩阻力而引起的波能损失更大，而礁坪宽度越大意味着波浪传播需经过更长的路程，导致波能衰减量越多[5–6]，对于岸滩坡度相近的P1 和P3 剖面来说，P1 剖面由于礁体水深较小且礁坪宽广，短波波能损失较大，导致到达近岸短波波能较小，相反，P3 剖面由于礁体水深较大且礁坪宽度较小，其短波波能损失较小，到达近岸短波波能更大。礁冠处由于水深突变，进而引起破波点处更大的湍动能，波浪破碎效应更强烈，相对无礁冠结构礁体，存在礁冠结构的礁体对入射波能削弱性更大[7–8]。故导致礁坪宽度最窄的P2 剖面近岸短波剩余波能是3 个剖面中最小，就因其礁缘处存在礁冠结构。

波浪破碎同样也会导致次重力波波能衰减，但与此同时，基于移动破波点机制的驱动，波能由短波频段向次重力波频段转移，对波浪的落后与超前时间相关分析或谱分析都发现了礁缘附近次重力波生成的现象[27–30]。礁坪宽度、礁体水深和岸滩坡度对次重力波波能损耗影响与对短波类似[3–5]。P1 剖面破波带外岸坡反射性强，但其礁坪浅且宽广，到达近岸时短波和次重力波波能都衰减显著，而P3 剖面礁体水深较大，进而导致其近岸短波和次重力波波能较大。P2 剖面礁坪宽度小，次重力波波能衰减量相对较少。由于各剖面地形的差异影响，对应剖面短波波能和次重力波波能沿程呈现不同变化规律，最终导致礁后海滩的近岸波能主控频段的差异。P1 和P3 剖面近岸短波波能均大于次重力波波能，导致这两个剖面近岸波能以短波频段为主，相反，P2 剖面近岸短波波能小于次重力波波能，导致该剖面近岸波能以次重力波频段为主。

4.2 礁后海滩动力地貌特征

徐闻西落港珊瑚礁海岸3 条典型剖面珊瑚礁地形和礁后海滩地貌表现出明显的差异性，从动力地貌学角度两者是相互联系的。海滩地貌形态受近岸波浪、沉积物以及地质等多种因素影响，是区域波能在滩面耗散并驱动沉积物分配的结果，趋于形成海滩平衡剖面[31]。海滩平衡剖面形态模式有助于理解岸滩平衡剖面形态与近岸波能之间的关系。前人对海滩平衡剖面的研究众多[32–38]，其中最具代表性的是Dean 基于美国大西洋海岸和墨西哥海岸504 条海滩剖面的拟合结果，其提出的海滩平衡剖面模式，被广泛应用于浪控海滩。然而对于珊瑚礁海岸而言，礁体地形对礁后海滩水动力环境影响显著，该平衡剖面模式存在较大局限性，Muñóz-Pérez 等[9]基于Dean 的海滩平衡剖面模型，提出了适用于珊瑚礁海岸礁后海滩平衡剖面模型

上式拟合起点位于坐标系原点，根据本文实测海滩地形，对海滩平衡剖面拟合起点进行相应的平移转化

式中，h为拟合起点为坐标系原点的剖面高程（单位：m）；h′为拟合起点平移转化后的剖面高程（单位：m）；h0为岸线所在位置高程（平均大潮高潮线，单位：m）；x为离岸距离（单位：m）；x0为岸线位置（单位：m）；Arp、m为拟合常数；Muñóz-Pérez 等[9]取m=2/3。虽然该剖面模型形式与Dean 海滩平衡剖面模型一致，但其Arp值不同于Dean 模型中的A值。Arp与A满足

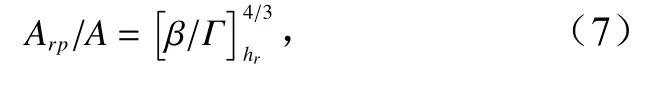
式中，Γ和β分别为受珊瑚礁保护和不受珊瑚礁保护剖面破波指数；hr为礁坪水深（单位：m）。

对于一个宽广的礁体（宽度→∞），Γ值位于0.35～0.55 之间[39]，而β值位于0.65～1.1 之间[40]，故Arp=1.250～4.604A。基于Muñóz-Pérez 等[9]礁后海滩平衡剖面形式对研究区礁后海滩进行拟合，计算误差ε（式（6））并取误差最小的拟合值Arp（图8，表3）。拟合结果表明P1 和P3 剖面拟合误差较小，而P2 剖面拟合误差达36.6%，差异性较大。

表3 各海滩平衡剖面拟合结果及误差Table 3 Fitting results and errors of each beach equilibrium profile

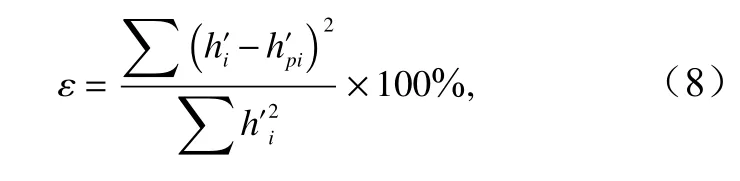
图8 徐闻西落港珊瑚礁海岸剖面处岸滩平衡剖面模拟Fig.8 Simulation of the beach equilibrium profile in the Xiluo Port,Xuwen

从海滩平衡剖面模型（式（6））数学形式上可知，拟合参数m的取值决定海滩剖面曲线的反射性强度，由前文分析可知P2 剖面反射性弱，而P1 和P3 剖面反射性较强，故P2 剖面与P1 和P3 剖面应采用不同的m值进行拟合。究其原因，Muñóz-Pérez 等[9]提出的珊瑚礁海滩平衡剖面模式是基于对西班牙南部海岸的珊瑚礁地形的研究而提出的，该区域礁坪水深都较大且礁体形态较平整，模型虽然考虑了珊瑚礁地形对波浪的作用结果，但未能体现不同礁体地形下的波浪传播差异以及该差异影响下波能主控频段的分布变化。不同礁体地形影响下的近岸波能主控频段是不同的，P2 剖面礁后海滩处波能主控频段为次重力波频段，而P1 和P3 剖面礁后海滩处波能主控频段为短波频段。因此，结合实测地形地貌结果、平衡海滩剖面拟合结果和礁后海滩波浪分布结果可知，不同频段波浪影响下，礁后海滩地貌特征呈现差异性特征，次重力波主控海岸滩面耗散性较强，呈侵蚀地貌类型；短波主控海岸滩面反射性较强，海滩相对稳定。