无抗冲切钢筋的RC板柱节点受冲切承载力计算

夏成亮，史庆轩，王 震

(1.结构工程与抗震教育部重点实验室(西安建筑科技大学)，西安 710055；2.西安建筑科技大学 土木工程学院，西安 710055)

板柱结构是一种以板和柱作为主要承重构件的结构体系，又称为无梁楼盖结构体系。该结构具有空间布置灵活，传力路径明确，结构层高较低，施工速度快等特点。以往的研究表明，板柱结构具有相对较低的抗弯刚度，在节点区域容易发生冲切破坏。由于在冲切破坏前板柱节点处于复杂的三维受力状态，剪力传递机制不明确，国内外对板柱节点冲切破坏的机理一直没有得出统一的结论，板柱节点的受冲切承载力计算方法大多都是基于简支板冲切试验提出的经验公式。

为完善无抗冲切钢筋的RC板柱节点的受冲切承载力计算方法，国内外学者进行了大量试验研究及理论分析。文献[1]对高强混凝土板柱节点的试验研究表明混凝土强度与节点受冲切承载力存在非线性关系。文献[2]考虑混凝土强度、钢筋的销栓作用影响对锥壳模型进行修正，通过对节点脱离扇形体建立平衡条件，推导了无抗冲切钢筋的RC板柱节点受冲切承载力计算式。文献[3]通过试验证明冲切破坏是节点区塑性转动使临界裂缝宽度增加导致，考虑截面高度，纵筋配筋率，骨料粒径、冲跨比等影响因素，推导出基于临界斜裂缝理论的无抗冲切钢筋的RC板柱节点受冲切承载力计算式。

本文认为板柱节点冲切破坏是由于板上部剪压区混凝土受压破坏和临界斜裂缝区域钢筋混凝土剪切失效共同导致。剪压区是临界斜裂缝未穿过的区域，其抗剪承载力由混凝土的抗压强度提供。临界斜裂缝区域的抗剪贡献则由混凝土间的骨料咬合力以及钢筋的销栓作用提供。本文使用修正压力场理论(MCFT)[4]计算无抗冲切钢筋的RC板柱节点临界斜裂缝区域的抗剪承载力，剪压区混凝土的抗剪承载力则在确定的剪压区范围内建立其计算表达式。通过对板柱节点冲切试验结果的验算,验证了本计算方法的正确性，为板柱节点受冲切承载力的计算提供理论依据。

1 冲切破坏机理及破坏模型

对以往无抗冲切钢筋的RC板柱节点冲切试验的破坏面观察发现，在板和柱相交的位置存在混凝土局部压碎的情况。因此本文认为无抗冲切钢筋的RC板柱节点冲切破坏类似于梁剪压破坏，临界斜裂缝发展到一定程度后，将被剪压区混凝土阻断，存在明显的受压区与受拉区。由于板柱节点冲切破坏属于三维剪切破坏，假定冲切荷载由剪压区未开裂混凝土和临界斜裂缝区域(包括斜拉区和受拉区)的骨料咬合力及销栓作用共同承担。

图1 冲切破坏模型

无抗冲切钢筋的RC板柱节点的极限冲切承载力由受压区的承载力垂直分量和临界斜裂缝区域骨料咬合力组成：

Vu=Vc+Vcs

(1)

本文中剪压区混凝土提供的抗剪承载力Vc由文献[5]提出的分析方法建立计算表达式。临界斜裂缝区域混凝土提供的抗剪承载力Vcs基于修正压力场理论(MCFT)，不考虑抗弯钢筋的销栓力，通过迭代计算得到。

2 剪压区混凝土受冲切承载力计算

参考文献[5]研究梁剪切失效的方法，本文将节点区分割成临界斜裂缝隔离体I和与柱面接触的棱柱体II，不考虑柱面对直接接触的棱柱体II的影响，分别建立隔离体平衡条件，如图2所示，得到剪压区高度表达式：

图2 作用在节点单元上的力

(2)

式中：hs为剪压区高度，hc为受压区高度，h0为板有效高度，θ为临界斜裂缝倾角。

受压区高度由下式确定，取正根[5]：

(3)

式中：f′c为混凝土圆柱体抗压强度，ρ为板受弯钢筋配筋率。

在极限状态下，假定受压区混凝土压应力σz符合抛物线分布规律且应变分布为倒三角形，并且压应力σz在混凝土受压区最外边缘处达到混凝土抗压强度f′c，则从受拉钢筋中心至中性轴z处的混凝土纵向正应力σz可按式(4)计算[6]：

(4)

在剪压区高度hs范围内对混凝土压应力σz积分，得到剪压区混凝土的受剪承载力Vc贡献表达式：

(5)

式中c为柱截面尺寸。

3 修正压力场理论(MCFT)

修正压力场理论(MCFT)[4]是由加拿大学者Vecchio和Collins采用非线性混凝土本构，通过对开裂混凝土单元建立平衡方程和相容方程，提出的一种计算正交双向承受薄膜应力的钢筋混凝土平面单元受剪承载力的方法。随着荷载持续增大，节点区形成临界斜裂缝并发展到受压区，在裂缝处正应力与剪应力的共同作用下节点发生冲切破坏。本文在修正压力场理论的基础上推导无抗冲切钢筋的RC板柱节点临界斜裂缝区域的受冲切承载力。

3.1 MCFT应变协调条件

根据修正压力场理论(MCFT)[4]中钢筋与混凝土完全黏结的假定及应变莫尔圆理论，可得到开裂混凝土单元的应变协调条件：

εx=εcx=εsx

(6)

εy=εcy=εsy

(7)

εx+εy=ε1+ε2

(8)

(9)

式中：ε1、ε2分别为垂直于裂缝的平均主拉应变和平均主压应变，εx、εy分别为平均横向应变和平均纵向应变，εcx、εcy分别为混凝土横向应变和纵向应变，εsx、εsy为分别为横向钢筋应变和纵向钢筋应变。

3.2 MCFT平衡条件

将修正压力场理论(MCFT)[4]中的钢筋单元和开裂混凝土单元叠加得到图3(a)所示的开裂钢筋混凝土单元的应力状态。根据图3(a)所示的开裂钢筋混凝土单元的应力状态和图3(b)所示的混凝土平均应力莫尔圆，可得到平衡条件：

图3 开裂钢筋混凝土应力状态与混凝土平均应力莫尔圆

τ=τcxy

(10)

σcx=σc1-τcxy/tanθ

(11)

σcy=σc1-τcxytanθ

(12)

σc2=σc1-τcxy(tanθ+cotθ)

(13)

式中：σc1、σc2分别为开裂混凝土的主拉应力和主压应力，σcx、σcy分别为混凝土在x和y方向上的平均应力，τ为开裂钢筋混凝土单元的剪应力，τcxy为开裂混凝土单元的平均剪应力。

修正压力场理论(MCFT)[4]认为裂缝引起的局部应力对开裂混凝土单元的极限承载力有重要影响。考虑裂缝之间的局部应力可得到混凝土单元在裂缝处及裂缝间的平衡方程：

σsxcr=(σc1+τcicotθ+σsx)ρsx

(14)

σsycr=(σc1-τcitanθ+σsy)ρsy

(15)

式中：τci为裂缝表面的剪应力，σsxcr、σsycr分别为裂缝处的横向钢筋和纵向钢筋的应力，σsx、σsy分别为裂缝间横向钢筋和纵向钢筋的平均拉应力，ρsx、ρsy分别为横向钢筋和纵向钢筋的配筋率。

3.3 开裂混凝土本构关系

3.3.1 混凝土本构

由于在拉-压双轴应力状态下的混凝土比标准圆柱体混凝土强度更低、更脆，因此修正压力场理论(MCFT)[4]采用考虑混凝土软化现象的混凝土受压应力-应变关系：

(16)

(17)

受拉应力-应变关系为：

当ε1≤εcr时：

σc1=Ecε1

(18)

当ε1>εcr时：

(19)

式中：Ec为混凝土弹性模量，ε′c为混凝土峰值压应变，εcr为混凝土开裂应变，fc2max为混凝土受压方向上的极限压应力。

3.3.2 钢筋本构

修正压力场理论(MCFT)[4]假定钢筋轴向应力仅取决于轴向应变参数，并假定垂直于钢筋截面的剪应力为零，其应力-应变关系采用理想弹塑性模型：

σsx=Esεsx≤fsy

(20)

式中：Es为板内纵筋弹性模量，εsx为钢筋应变，fsy为板内纵筋屈服强度。

4 无抗冲切钢筋RC板冲切承载力计算

4.1 计算方法与步骤

修正压力场理论(MCFT)[4]假定混凝土开裂后拉应力仍参与抗剪，由图4所示的无抗冲切钢筋的RC板开裂后的内力平衡可知，在两条裂缝间的混凝土拉应力达到最大值。选取临界斜裂缝与竖向平面截取的棱柱体作为分析对象，棱柱体应力分布与开裂RC板相同，通过对柱面与棱柱体相互接触的平面上的应力积分来计算板的极限承载力。假定柱面与棱柱体相互接触的平面上的剪应力均匀分布，则单块棱柱体的冲切破坏截面的剪应力τ为：

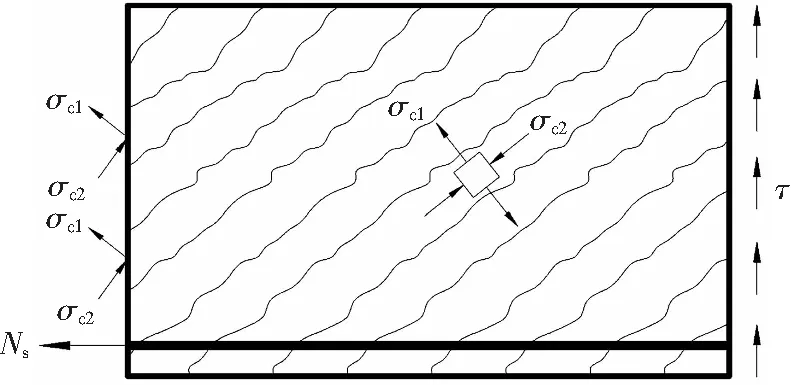
图4 受剪混凝土的主应力

(21)

式中：h为板厚，Vcs1为单块棱柱体承受的剪力。

通过建立棱柱体在水平方向上的力的平衡条件可得:

εx=(σc2cos2θ-σc1sin2θ)/(ρsxEs)

(22)

根据修正压力场理论，当板未布置抗冲切钢筋时,裂缝处的平均应力平衡关系见图5(a)，临界斜裂缝上存在钢筋拉应力σsx和混凝土主拉应力σc1；两条裂缝间的应力平衡关系见图5(b)，存在局部剪应力τci和局部压应力σci，其中局部压应力σci很小，可以忽略不计。在给定外力作用下，这两组应力状态应该是应力等效的。因此可得到：

图5 计算平均应力与裂缝处的局部应力

σc1sinθ+ρsxσsxsinθ=ρsxσsxcrsinθ-τcicosθ

(23)

σc1cosθ=τcisinθ

(24)

由式(23)可得，未配置抗冲切钢筋的RC板柱节点冲切破坏时的最大主拉应力:

σc1max=τcitanθ

(25)

对于无抗冲切钢筋的RC板柱节点，联立式(10)、式(12)和式(25)可得:

τ=τci

(26)

基于文献[4]对混凝土裂缝截面骨料咬合力的研究，当局部压应力σci很小时，可得到局部剪应力表达式:

(27)

式中：ag为混凝土材料的最大骨料粒径，ag通常可取为20 mm，w为钢筋混凝土开裂单元的平均裂缝宽度，当不配置抗冲切钢筋时，可由下式计算:

(28)

式中：Smx为垂直于x方向的裂缝间距，当钢筋混凝土板在板顶、板底布置双层钢筋网时，Smx为抗弯钢筋在垂直方向上的间距；根据文献[7]的研究，Smx可近似取0.9h0。

临界斜裂缝倾角θ是确定冲切锥几何形状和冲切承载力的重要参数，文献[8]通过线性拟合得到了倾角θ与抗弯钢筋配筋特征值ρsfy/fc的相关性表达式。本文通过对以往试验数据的统计分析，发现倾角θ和柱截面周长与板有效厚度之比Cc/h0及ρsfy/fc显著相关。因此，本文认为影响节点临界斜裂缝倾角θ的因素主要为Cc/h0和ρsfy/fc，假定θ由以下方程式表达：

θ=a(Cc/h0)α(ρsfy/fc)β

(29)

为了确定待定系数α和β，采用文献[9]中的分析方法，分别检验单一变量对临界斜裂缝倾角θ的影响，可以得到单一变量影响系数(α和β)变化过程中对临界斜裂缝倾角平均偏差ē的变化规律，如图6所示。由图可知，α和β与临界斜裂缝倾角平均偏差ē呈明显非线性关系，存在某一极值点使ē达到最小值。由分析结果确定待定系数后，可得到倾角θ的最终表达式：

图6 样本平均偏差-影响因数曲线

θ=32(Cc/h0)-0.12(ρsfy/fc)-0.08

(30)

将上述公式计算的倾角与试验值对比，本文拟合公式均值为1.09，变异系数为0.20；文献[8]拟合公式均值为1.13，变异系数为0.20。通过表1中试验值与计算值对比可知，本文拟合的公式不受文献[8]中35°上限角的限制，且对除方形柱以外的其他柱截面形状的节点预测结果较好。因此，本文拟合的角度计算公式能较好预测冲切斜裂缝倾角。

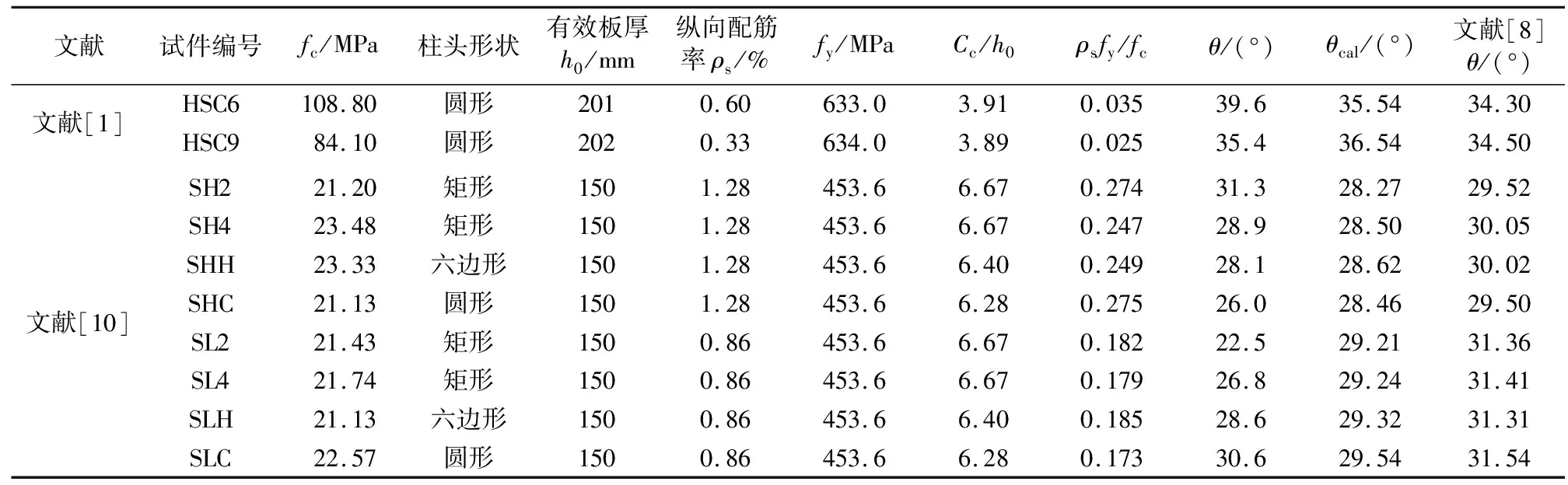
表1 冲切裂缝倾角试验值与计算值对比

由式(20)、(26)、(27)可得，无抗冲切钢筋的RC板柱节点在x方向上的抗冲切承载力为

[2c+2(h-hs)cotθ](h-hs)

(31)

将式(5)和式(31)代入式(1)得到节点抗冲切承载力

[2c+2(h-hs)cotθ](h-hs)

(32)

节点受冲切承载力计算流程见图7。

图7 节点受冲切承载力计算流程

4.2 计算结果与试验值对比

为验证本文提出的冲切承载力计算方法的准确性与适用性，采用式(32)对相关文献中54个[1-2,8,10-21]无抗冲切钢筋的RC板柱节点在竖向荷载作用下的抗冲切试验结果进行验算。节点试验的混凝土立方体抗压强度变化范围为27.5～124.87 MPa，柱截面尺寸变化范围为130～520 mm, 冲跨比λ变化范围为2.83～7.13，纵筋配筋率ρs变化范围为0.33%～1.73%，节点支承方式均为板四边简支，收集的试验数据具有一定的代表性。图8(a)为文献[21]的理论公式计算结果与试验值对比。图8(b)为本文公式(32)的计算结果与试验值对比。由图可知，文献[21]的计算值与试验值比值的平均值、标准差、变异系数分别为0.771、0.147、0.191；本文提出的计算方法的计算值与试验值比值的平均值、标准差、变异系数分别为1.005、0.163、0.162。通过对比可知，采用本文提出的方法计算出的节点抗冲切承载力与试验值较为接近，并且具有较小的标准差和变异系数，表明本文提出的无抗冲切钢筋的RC板柱节点冲切承载力计算方法较为合理。

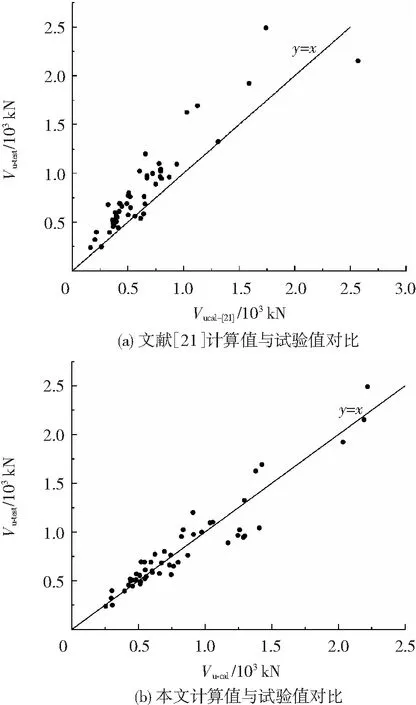
图8 计算值与试验值对比

5 结 论

1)本文通过对大量板柱节点冲切裂缝倾角试验数据的总结，对影响冲切裂缝倾角的因素进行统计分析，得到临界斜裂缝倾角θ和柱截面周长与板有效厚度之比Cc/h0及抗弯钢筋配筋率特征值ρsfy/fc之间的相关性表达式。通过对文献中冲切斜裂缝倾角的验算，证明该关系式能较准确的预测无抗冲切钢筋的RC板柱节点的冲切斜裂缝倾角。

2)将无抗冲切钢筋的RC板柱节点的冲切破坏模式类比梁的剪压破坏，结合修正压力场理论(MCFT)，分析板柱节点剪压区与临界斜裂缝区域(包括斜拉区和受拉区)不同的受力状态，推导无抗冲切钢筋的RC板柱节点的受冲切承载力计算式，分别计算剪压区与临界斜裂缝区域的冲切承载力贡献。通过对文献中大量试验结果的验算，以及与文献中冲切承载力计算值的比较，验证了本文提出的计算方法的准确性及适用性。