基于高频方波注入的IPMSM新型I/f控制策略
2022-03-23曲林峰邱建琪史涔溦
曲林峰, 邱建琪, 史涔溦
(浙江大学 电气工程学院, 浙江 杭州 310027)
永磁同步电机(permanent magnet synchronous motor, PMSM)因其具有体积小、结构简单、功率密度大、动态性能良好及功率因数高等诸多优点,被广泛应用在各种工业控制领域。
为实现对永磁同步电机进行高性能磁场定向控制,转子位置信息的获取非常重要。而传统的机械位置传感器使电机的体积增大,成本上升,在一些特殊应用场合不允许被安装使用[1]。所以许多海内外学者对无传感器控制进行了深入的研究,根据转速状态范围的不同主要分为低速和中高速2方面。其中中高速工况下的方法主要有:模型参考自适应法[2]、扩展卡尔曼滤波法[3]和滑模观测器法[4]等等。但由于反电势和电机转速成正比,在低速情况下反电势的值很小,信号解耦精度不理想。所以在电机低速的工况下根据电机的凸极特性进行转子位置信息获取,主要有高频旋转注入法[5]、高频脉振注入法[6]和高频方波注入法[7]等等。
传统的I/f控制策略方法简单、易于实现[8],但是这种开环策略存在效率低、容易失步等缺点,因此对其进行闭环改进成为很有价值的研究方向。文献[9]中基于电机有功功率变化和转速变化的正相关性,通过有功反馈量对电机给定角频率进行调整;NAIR等[10]增加了转矩控制器来调节给定斜坡角频率信号的斜率,提高启动的动态性能。但以上方法均无法实现对给定电流的闭环控制。BORISAVLJEVIC等[11]提出通过电流调节器生成参考电压,保留与V/f控制的方法调频,具有对给定电流监控的优势,但不能根据外部负载动态地调整I/f曲线。周成林[12]提出了一种将高频正弦信号引入参与闭环调节的控制策略,但增加了过多的滤波器。王萌等[13]通过引入电机实时功率对电流进行调节,但控制算法中使用无功功率与输出电流的比值做解析计算,可能会造成系统电流波动过大甚至持续波动。文献[14]中提出了一种改进方法:速度环基于有功功率扰动分量调节电流矢量转速,电流环通过实时观测无功功率对给定电流幅值的大小进行闭环调节。
课题组在综合上述方法的基础上,提出了一种改进的I/f控制策略,将传统的I/f控制方法和高频方波注入法相结合,对I/f进行给定电流闭环调节,提高了电流的使用率和电机的控制效率,并对信号处理环节进行简化。与传统的高频方波注入法相比,课题组提出的方法简化了信号处理的过程,通过对虚拟δ轴电流信号进行解耦对电机的位置误差角闭环调节,省去了传统控制策略中使用的观测器或锁相环环节,简化了计算处理过程。最终通过实验验证了本研究方法在电机启动和低速时具有良好的控制性能。
1 开环I/f控制策略原理
1.1 I/f控制系统及电机物理模型
传统的I/f控制策略对永磁同步电机的速度开环控制、电流闭环控制,相较于纯开环的V/f控制方法,其动态性能更高,改进了电流易失控等弊端。


图1 传统开环I/f控制框图Figure 1 Block diagram of traditional open-loop I/f control
选择内嵌式永磁同步电机(insert permanent magnet synchronous motor, IPMSM)作为课题组分析对象,其物理模型电磁转矩为:
(1)
式中:Te为电机电磁转矩;np为电机的极对数;id和iq分别为d-q轴系电流;Ψf为永磁体磁链;Ld和Lq分别为d-q轴电感。
机械运动学公式为:
(2)
式中:J是系统转动惯量,ωr为电机系统机械角速度,TL代表负载转矩,B代表阻尼系数。
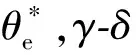
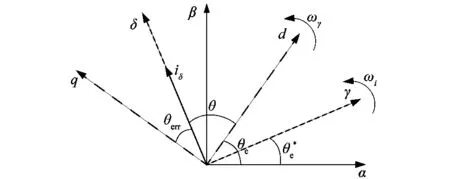
图2 γ-δ坐标系与d-q坐标系的相位关系图Figure 2 Phase relationship between γ-δ coordinate system and d-q coordinate system
(3)
在开环I/f控制下给定的γ轴电流为0,d-q轴系与轴γ-δ系之间的电流存在如下关系:
(4)
综合(1)式,可得此时的电磁转矩为:
(5)
1.2 IPMSM转矩-功角自平衡原理分析
如图3所示,I/f控制模式下,真实的转子位置信息不可知。对电机进行初始预定位,初始时刻δ轴与d轴重合,iδ均用来励磁,电机的初始转矩为0。随着斜坡函数与积分积累使得位置角逐步增加,功角θ逐渐增大,iδ在q轴上的投影iδsinθ逐步增大,则电机的电磁转矩增加,当大于负载转矩时,电机正向启动。
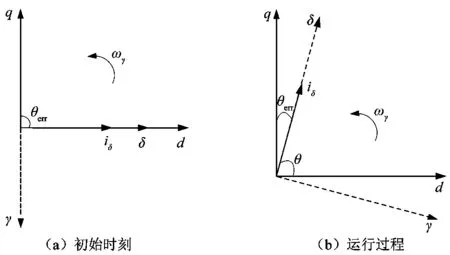
图3 功角变化示意图Figure 3 Schematic diagram of power angle change
结合式(2)和图2分析可知,在启动过程中,若负载TL增大,电机转速下降,γ-δ轴系和d-q轴系之间的夹角将变大,iδ在q轴上的投影分量增大,电磁转矩增加,与负载TL平衡时将达到新的稳态。反之若负载突然减小,同理电机转速增大,功角θ逐渐减小,iδsinθ逐渐减小,再次与负载转矩相同,电机再次达到稳态。因此在I/f控制方法下可以通过调整功角θ来实现电磁转矩和负载动态平衡,存在“转矩-功角自平衡”。而当负载过于增大,超过电机输出极限时,电机进入失步状态。
对IPMSM功角的极限进行分析,当功角θ增加,转矩Te不再单调递增达到拐点时,无法满足稳定条件。即:
(6)
(7)
因此功角稳定范围为:
θ∈(-θmax,θmax)。
(8)
2 I/f与高频方波注入相结合的控制策略
2.1 无观测器转子位置信息的获取
传统的I/f控制存在给定电流为固定值无法调控、电流利用率低、转速开环不能瞬时调节等诸多问题。课题组提出一种新控制思路:将传统的I/f控制与高频方波注入法相结合,并对信号解耦提取做进一步的优化处理,从δ轴系电流分离出目标误差角信号,省去了观测器环节,简化了繁琐的计算过程,提高系统控制效率。I/f与高频方波注入相结合的控制策略其主要思想控制框图如图4所示。
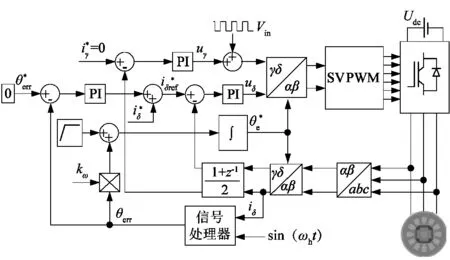
图4 开环I/f与高频方波注入法相结合控制框图Figure 4 Control block diagram of open-loop I/f combined with high frequency square wave injection method
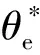
2.2 转子位置角的提取
构建电机在d-q轴系下的电压方程为:
(9)
式中:ud,uq,id,iq分别为d-q轴系下的电压与电流;R为定子电阻;Ld,Lq分别为d-q轴的电感;ωe为电角速度;Ψf是电机永磁体的磁链。
在低速时,电机的反电势值很小可以忽略。电机注入的高频信号频率远远大于基波频率,因此电阻的阻抗也可以忽略,视为纯感性负载,在高频下简化的电压方程为:
(10)
式中:udh,uqh,idh,iqh分别为d-q轴系下高频电压与高频电流。
由图2所示,d-q轴系与γ-δ轴系之间的关系为:
(11)
d-q轴系与α-β轴系之间的关系为:
(12)
注入的高频方波信号为:
(13)
注入高频信号后在γ-δ轴系下电流idq由基频分量idql和高频分量idqh合成而成,提取高频电流获取转子的位置信息。如图5所示,注入的高频方波频率和三相PWM频率相等,每个周期内对电流采样2次。由于注入频率和采样频率很高,在1个周期内电流的基频分量变化不大,视为定值偏置。利用式(14)相邻2次电流求和获得低频电流,利用式(15)相邻2次电流作差获得高频电流。
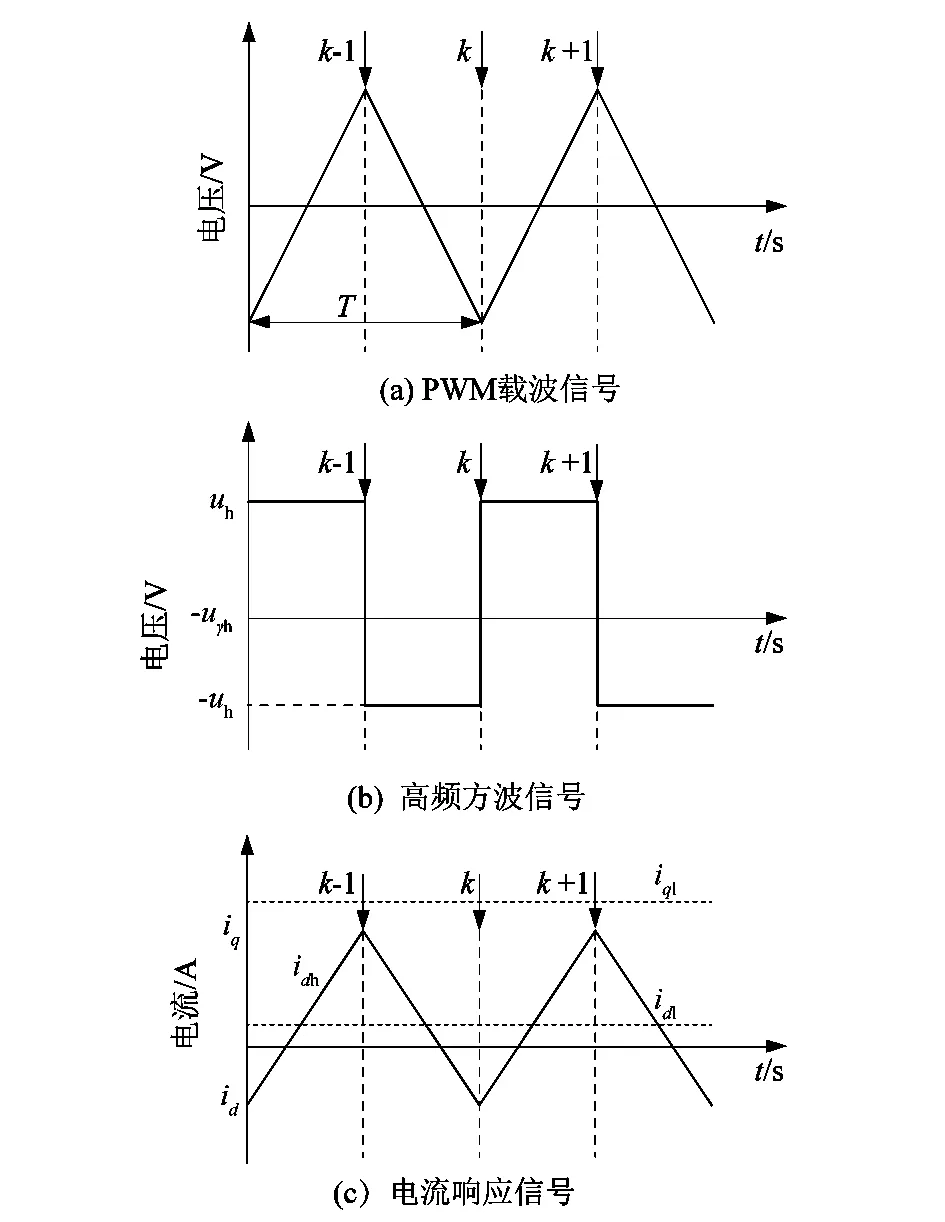
图5 高频注入信号和电流响应时序图Figure 5 Timing diagram of high frequency injection signal and current response
(14)
(15)
综合式(10)~(13)可得:
(16)
iγh和iδh前后2次采样电流的差值Δiγh和Δiδh分别为:
(17)
(18)
对式(18)周期性方波函数而言,通过傅里叶分解可以展开成若干不同奇数频率的正弦波相迭加:
(19)
式中ωh为高频方波信号的频率。


图6 信号处理方式Figure 6 Signal processing block diagram
(20)
其中k为固定值系数,当误差角很小时,其正弦值约等于自身弧度。
ksin 2θerr≈k^θerr。
(21)
结合式(21),当误差角足够小的时候,式(20)可转化为:
(22)
式中:k1=2k^kp,k2=2k^ki。
传统的I/f速度环为开环,只有给定电角速度ω*。在本研究中利用反馈的误差角信息θerr对角速度做闭环正反馈。与开环的I/f控制策略相比,本节中提出的控制策略对IPMSM固定的给定电流做闭环调节,改善了电流的利用率低的问题,提高电流响应的动态性能。对电机的速度做闭环调节补偿,与开环I/f相比提高了系统的抗扰动能力。该方法亦省去了传统的方波注入法中的锁相环与观测器环节,一定程度上简化了复杂的信号解耦与参数整定,使得由电流获取转子位置信号的方法更为简单。
3 实验验证与分析
为了实验验证课题组提出的改进型I/f与高频方波注入混合控制策略,搭建了如图7所示的实验控制测量平台,对电机启动和负载突变进行实验测试。其中:A为Tektronix TPS 2024示波器;B为直流稳压源,输出110 V直流电压为三相逆变器提供母线电压;C为CCS上位机控制软件;D为实验所用的控制板与功率板,德州仪器的TMS320F28035为本实验采用的控制芯片;E为被控对象4对极永磁同步电机;F为磁粉调速器,为电机E提供负载转矩。


图7 实验平台实物图Figure 7 Picture of experimental platform
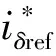
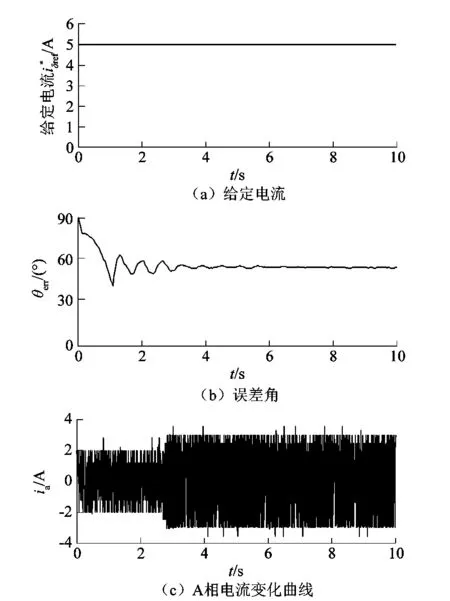
图8 传统开环控制策略下各变量波形Figure 8 Variable waveforms under open-loop control strategy
改进的I/f控制与高频方波注入相结合的策略中注入高频方波电压信号的频率为5 kHz,幅值为18 V,电流采样频率为10 kHz。图9所示为该方法下电机启动至稳态的动态过程中各变量变化曲线。转速从0逐渐上升到300 r/min,δ轴电流给定值由5 A逐渐下降到3 A左右,轴系夹角最终收敛到0°左右,A相电流幅值启动过程中逐渐衰减,最终稳态,远低于传统方法中的5 A。通过将2种策略对比可以得出:改进的控制方法实现了对给定电流的闭环可控,减小了轴系夹角,改进了传统I/f方法的弊端,提高了电流的利用率,降低了电机的铜损,提升了系统的效率。
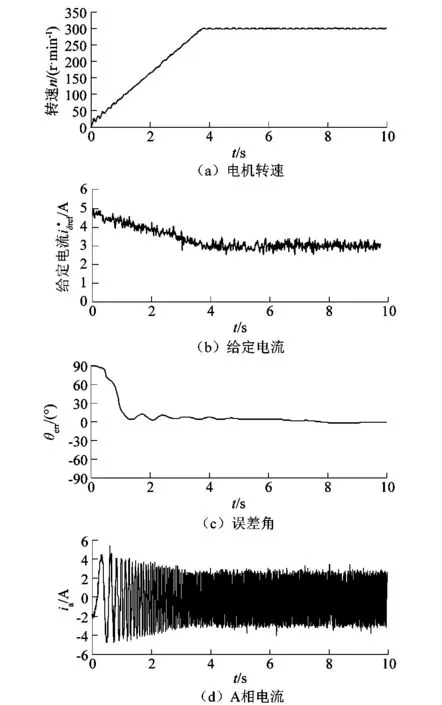
图9 混合控制策略下启动到稳态各变量波形Figure 9 Variable waveforms under mixed control strategy
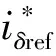

图10 突减负载时各变量波形Figure 10 Experimental waveforms with decreasing load torque decreasing
同理,突增负载时各变量波形如图11所示。在2.6 s左右时突增负载,实际的转子轴系角速度下降,电机转速下降到225 r/min左右,轴系间误差角跌至-23°左右,电流逐步增大,通过“转矩—功角自平衡”效应和混合控制策略的闭环反馈调控后,最终达到新的稳态,电流收敛到3 A左右。通过负载突变实验证明了课题组提出的方法使得系统的转速和电流具有较好动态性能,提升了系统的抗扰动能力。
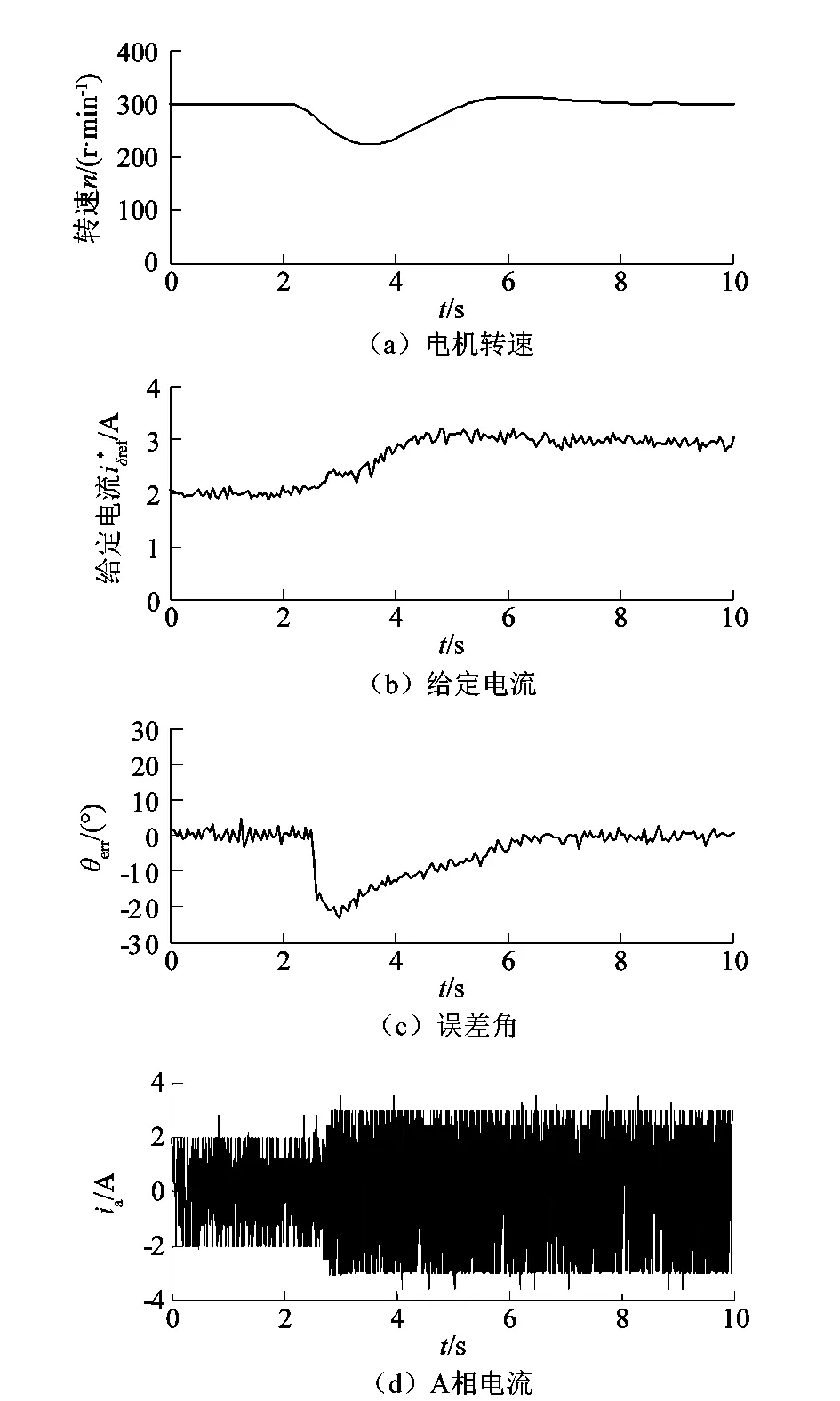
图11 突加负载时各变量波形Figure 11 Experimental waveforms with increasing load torque increasing
4 结语
针对传统的I/f控制方法存在的给定电流无法调节等缺点,课题组提出了一种改进的控制策略:将高频方波注入法与I/f控制方法相结合,并进一步对转子位置角提取环节进行简化,省去了复杂的信号处理与参数整定环节。通过实验证明了该方法可以达到预期的效果,轴系间误差角可以稳态至0°左右,提高了电机电流的利用率和系统的控制效率,具有良好动态抗扰性能,与I/f方法相比系统性能有较大改进。
