弯曲通道内黏弹性流体二次流现象的数值研究

2022-03-23刘唐京王企鲲

轻工机械 2022年1期

刘唐京，王企鲲,2*，邹赫

(1.上海理工大学能源与动力工程学院，上海 200093；2.上海理工大学上海市动力工程多相流动与传热重点实验室，上海 200093)

在一定条件下，流体流经弯曲管道在其截面上会产生二次流，其产生机理在于离心力所引起的管中心流体与边壁流体的动量差[1]。针对这个现象，国内外有很多学者通过解析求解、实验和数值模拟等方法对弯曲管内流动进行了大量的研究。DEAN[2-3]通过求解N-S方程发现了弯曲管道内存在双涡旋结构的二次流——迪恩涡。DATTA等[4]通过实验与数值模拟方式对螺旋管道内的湍流流动进行了研究。对于牛顿流体，只有流经弯曲通道，在惯性和曲率的影响下才会有二次流的产生。相比之下，黏弹性流体却有很大的不同，即使在没有惯性和曲率的情况下依然能产生二次流。LI等[5]63发现黏弹性流体在矩形截面直管中也产生了二次流，因此黏弹性流体对于二次流的产生是有强化作用的。POOLE等[6]对蛇形管中黏弹性流体的流动现象做了探究，研究了曲率半径、截面高宽比和总黏度比对二次流强度的影响。SUN等[7]对麦克斯韦流体流经矩形截面弯曲管道的不可压缩流动进行了数值模拟，详细讨论了大迪恩数、德博拉数和曲率对流体流动特性的影响。

而在弯曲方形截面通道中黏弹性流体对于二次流影响的研究还是比较缺乏的。课题组主要是利用模拟仿真软件(FLUENT)来探究魏森贝格数Wi、溶质黏度比β以及管道的几何结构对黏弹性流体二次流强度的影响。弯管内二次流的研究，对于工程中利用弯管来加强管内对流、换热等有一定的理论指导作用。

由于FLUENT计算流体动力学代码中没有黏弹性流体的本构模型，用户需要自行定义并导入FLUENT中，详情可参考文献[8]。微分型黏弹性流体模型对任意黏弹性流体流动具有很好的通用性，能真实地描述黏弹性流体流动特性。其主要本构模型有Oldroyd-B模型[9]、FENE-P模型[10]和Giesekus模型[11]。LI等[5]61通过对黏弹性流体流动中二次流的准确预测，证明了利用UDF将Giesekus本构模型嵌入FLUENT软件的可行性。课题组采用Giesekus模型进行研究，探究黏弹性流体对弯管内二次流的影响因素。

1 计算模型与方法

1.1 计算模型与网格划分

POOLE等[6]就各种比例的通道截面对二次流强度的影响进行了研究，发现方形截面管道所产生的二次流强度最大。课题组亦采用截面方形弯管进行数值模拟，它由2段直管道与4段半圆弯曲管道组成，其截面边长为10 mm。为了尽可能消除入口效应，在弯曲段入口前预留10倍当量直径的直管段(方形弯管的当量直径即其截面边长)。方形弯管的结构参数见表1，表中d为弯管的当量直径，R为弯曲管道的曲率半径。将描述管道弯曲程度的曲率比定义为曲率比rc，即rc=d/2R。

表1 管道结构参数Table 1 Pipeline structure parameters

使用ICEM对方形弯管进行网格划分，在弯曲管道近壁面处进行网格加密处理，对整个流体域采用六面体结构化网格。为了保证计算的准确性和经济性，课题组对网格进行了无关性验证。计算工况为Ⅰ号管，Re=40，Wi=0.7，β=0.5，结果如图1所示。从图中可看出，当网格数大于70万时，不同网格数的计算结果误差非常小。同时考虑到计算经济性，对于后面的数值模拟计算，网格数量均控制在70万左右。Ⅰ号管计算模型如图2所示。

图1 网格无关性验证Figure 1 Grid independence verification

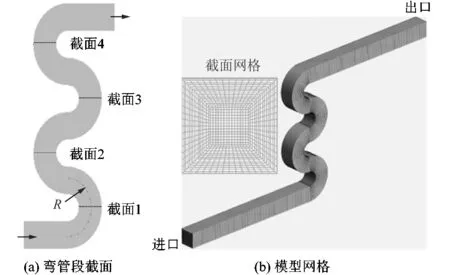
图2 Ⅰ号管计算模型Figure 2 Calculation model of pipeⅠ

1.2 计算方法

牛顿流体与黏弹性流体有着不同的流动特性，课题组选用Giesekus模型来表现流体的黏弹性特征。考虑流动是三维、不可压缩、层流和等温的，连续性方程和动量方程可所示为：

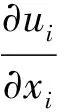
(1)

(2)

式中：ui为速度分量；xi为笛卡尔坐标系下的坐标分量，i=1,2,3；ρ为密度，其值为998.2 kg/m3；p表示压强；τij是应力张量。

对于黏弹性流体，τij表示为：

(3)

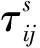
(4)

(5)

式中：μs为溶剂黏度，其值设为1×10-3Pa·s；μp为聚合物或表面溶质黏度；λ为松弛时间；δij为Kroneker符号，i=j时取值为1，i≠j时取值为0；f(r)为Peterlin函数，对于Giesekus模型，f(r)=1；Cij为聚合物或表面活性剂分子的变形率张量。

Cij的输运方程为：

(6)

计算工况的选取及数据分析都是基于量纲为一的参数，将描述黏弹性流体流动的雷诺数Re、魏森贝格数Wi和溶质黏度比β定义如下：

(7)

式中：um为主流平均速度；d为特征长度，这里选取管道截面边长；μ0=μs+μp。

④Ⅳ号Mo矿体：矿体宽度4.8m，Mo最高品位0.066×10-2，平均品位0.033×10-2，其中样品TC16H88伴生Pb品位0.205×10-2；

二次流量纲为一的强度SV*定义为：

(8)

式中：A为横截面积，u为沿着x轴方向的流速，w为沿着z轴方向的流速。

1.3 求解格式与人工黏性系数

在FLUENT中用双精度进行计算，采用COUPLED格式来处理速度与压力的耦合，压力方程的离散采用标准格式，动量方程和用户自定义标量方程的离散采用QUICK格式。为了使计算能够收敛，在式(6)中添加了人工黏性项，通过调整人工黏性项系数κ，使得每个计算工况都能得到收敛解。对于不同的Re数和Wi数都存在临界人工黏性系数κc，当小于这个临界值时，计算将会发散。表2给出了各工况下的κc值。

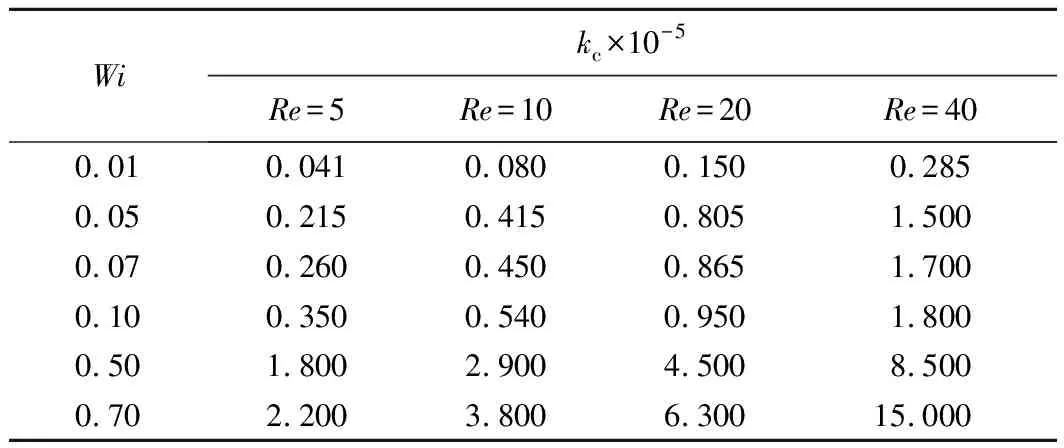
表2 临界人工黏性系数Table 2 Critical artificial viscosity coefficient m2/s

为了得到每一工况下合适的人工黏性系数κ，针对κ值对计算结果的影响进行了研究。表3给出了工况为Ⅰ号管，Re=40，Wi=0.7，β=0.5，不同κ值下的二次流强度。从表3中可看出，二次流强度是随着κ值的增大而减小的，其可能原因是较大的κ值带来了较大的耗散，从而弹性影响减弱。因此为了得到更准确的计算结果，对于每个计算工况，课题组均采用临界人工黏性系数。

表3 不同κ值下的二次流强度Table 3 Intensity of secondary flow under different κ

2 模拟结果与分析

2.1 溶质黏度比β对二次流的影响

溶质黏度比β的取值范围是0～1，它代表溶质的质量分数，当取β为0时，流体为牛顿流体。本次模拟选用Ⅰ号管道，雷诺数为40，β分别取0.1,0.3,0.5和0.7。图3显示了不同β值时管道截面1所对应的二次流强度。结果表明：β值越大即流体的黏弹性越强，在管道截面处产生的二次流强度就越高，这与文献[5]62页叙述采用直管模拟得到的结果类似。从图4中可看出，流体的黏度越高，在管道截面处的径向主流速度越大，从而加大了边壁流体与中心流体的动量差，产生的二次流因此加强。

图3 二次流强度随β变化趋势Figure 3 Trend of secondary flow intensity with β

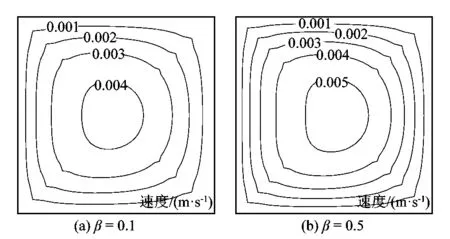
图4 截面1处的主流速度分布Figure 4 Mainstream velocity distribution at cross section 1

2.2 Wi数对二次流的影响

松弛时间λ是指在施加干扰之后，黏弹性流体达到另一平衡条件的特征时间。λ对一次流动和二次流动的强度都有很大的影响。λ越大，流体的性能越像固体；当λ达到零时，它为牛顿流体。

选用Ⅰ号管道进行仿真模拟，Re分别为5，10，20和40，β和α都设置为0.5时，Wi数的取值为0.01～0.70。输出各截面二次流强度取平均值，得到SV*与Wi的关系如图5所示。

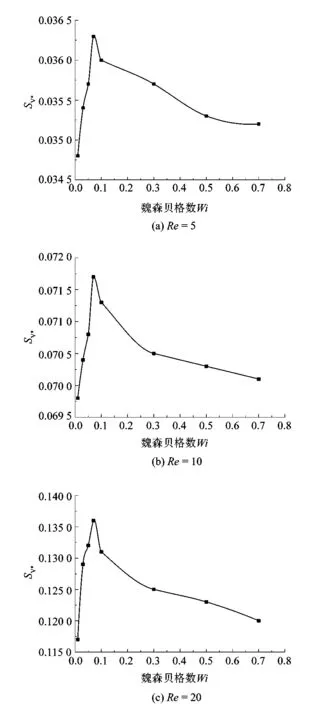
图5 不同Re下二次流强度随Wi的变化趋势Figure 5 Trend of secondary flow intensity with Wi under different Re

由图5可知，随着Re数的增大，管道内的二次流也相应地增强。随着魏森贝格数增大，二次流强度随之增大，在Wi约为0.09时达到峰值，之后又随着魏森贝格数的增大而减小。YUE[12]和LI等[5]62在对直管道的模拟探究中也观察到了这一点。其中YUE通过改变主流速来改变Wi，并且将这种现象归因于二次流的增加比主流速度增加得慢。为了排除这种影响，课题组与LI都采用了通过改变λ的方式来改变Wi。但即使提高Wi数，仍可实现λ与SV*之间的非单调关系。这意味着至少存在2个相互对立的效应，这些有竞争关系的效应主导了λ增大期间二次流的产生。针对这个现象LI做出如下推测：一方面，如果λ为零，则对应于牛顿流体，通过直管道的层流中就没有二次流；另一方面，如果λ为无穷大，对应于完全弹性或完全刚性材料，则不会有二次流产生。这种推测同样可以解释在文中弯管内所出现的这种现象。不同的是，λ为零时弯管截面处仍然有二次流的产生，这主要靠离心力作用造成边壁流体与管中心流体的动量差。

2.3 曲率比rc对二次流的影响

在POOLE等[6]12的研究中，选用了连续的半圆形弯道进行数值模拟，并且提出在松弛时间与逗留时间的比值较小时，前弯对后弯的影响比较小。课题组想要探究前弯对后弯的影响较大时，这种影响是否能够加强二次流强度以达到更强的掺混效果，连续的弯道是否能使二次流强度逐步增加或保持在较高的强度，以满足设计需求。

因此，在这种思路的指导下，课题组选用了类似的连续等曲率比管道。参数设置：Re为40，Wi为0.6，α为0.5，β为0.5。

曲率比对二次流的影响比较明显。如图6所示，当曲率比变大时，各个截面上的二次流强度都有所提升，曲率比越大，这种趋势愈发明显。

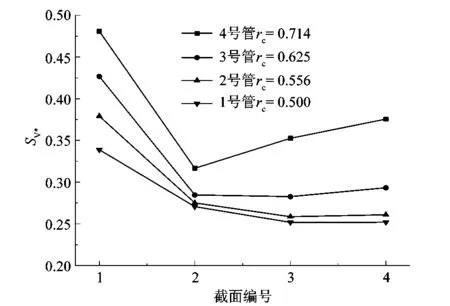
图6 不同曲率比弯道各截面二次流强度Figure 6 Secondary flow intensity in each section of bend with different curvature ratio

从图7的矢量图可发现，在经历多个弯道时，迪恩涡的涡心会朝着弯道的内侧移动，且相邻2个弯道的迪恩涡的旋转方向相反。对比1，2， 3和4号管道，可以发现第1个弯道对第2个弯道的二次流强度起到了抑制作用，而随着曲率比的增大，其余3个弯道中，前弯道对后弯道的二次流强度起到了积极作用。笔者认为在一定条件下，特定的曲率比对二次流强度起到很好的强化作用，如文中的4号管道。

图7 4号管各截面二次流矢量图Figure 1 Secondary flow vector diagram of each section of pipe 4

2.4 弯道数量对二次流的影响

由上文可知当曲率比较大(4号管道rc=0.714)时，从第2个弯道起，前弯道对后弯道的二次流强度都起到了积极作用。为了验证这个积极作用是否会一直持续下去，课题组在4号管道的基础上再增加了4个弯道(共8个)，并命名为5号管，同样在弯道中心处取截面，参数的设置与4号管道一样，如图8所示。

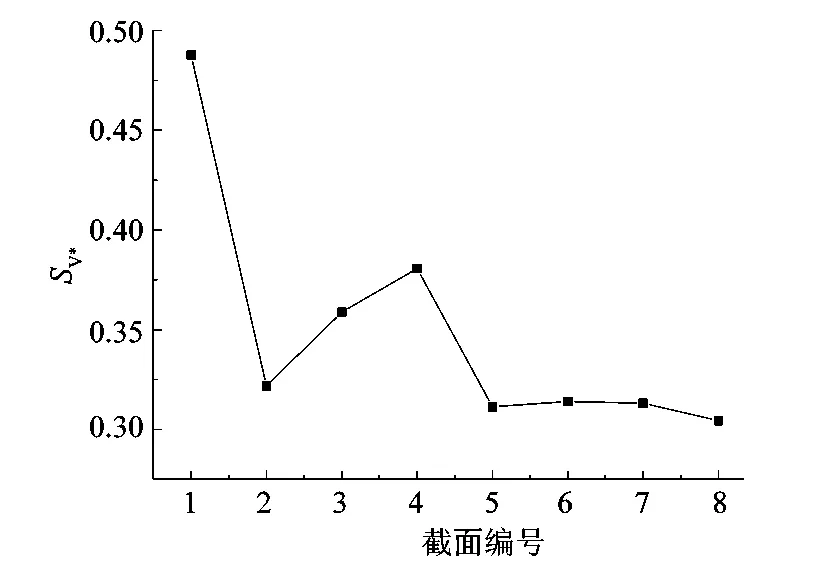
图8 5号管各截面二次流强度Figure 8 Secondary flow intensity of each section of pipe 5

图8显示，随着弯道数量的增加，前弯道对后弯道的积极作用并没有持续下去，这种积极的影响只延续到第4个弯道。而在之后的4个弯道中，由于前弯的影响，二次流的强度反而降低，尤其是在第5个弯道，二次流强度急剧下降。这说明在特定曲率比的弯管中，存在一个最优的弯道数量值，使管内的二次流强度达到最佳。本研究中的4号管，其弯道数量的最优值是4。