基于K-means 聚类与NSCT 的图像融合算法

李明明，王新赛，冯小二

（陆军炮兵防空兵学院郑州校区，郑州 450052）

0 引言

图像融合技术［1-3］是信息融合技术的一个重要分支，是指将不同传感器获取的图像信息，通过一定的图像融合算法，进行数据加工或整合，从而使融合图像更能满足人们对图像进一步处理（目标识别、特征提取）的目的。随着传感器技术的不断发展和信号分析技术的深入研究，图像融合技术已经在国防、生活等方方面面发挥着举足轻重的作用。本文研究的是一种基于可见光和红外图像的融合算法。在光学领域中，可见光技术和红外技术发展最为成熟，已经在安防、医疗、交通等各个领域得到了广泛的应用。

图像融合算法大体上可以分为空间域和频率域两大类。空间域算法是一种基于原始像素数据运算的方法，其主要优点是运算简单，信息涵盖全，缺点是对细节、边缘等处理效果不太理想，容易导致信息的模糊甚至缺失［4-7］。随着计算机运行能力的不断增强，使得基于频率域的图像融合算法得以实现。频率域算法是通过将图像的原始像素数据通过一定的数学方法得以转换，从而在“频率”上使得不同成分信息得到区分。从经典的傅里叶变换（Fourier）研究开展，不断展开了小波变换、轮廓波变换、非下采样轮廓波变换等分析理论和方法研究，由于NCST 算法同时具有多尺度、多方向、平移不变性等特征，成为频率域算法的主流。非下采样剪切波变换（non-subsampled contourlet transform，NCT）是由Cunha A.L.等人提出，主要是针对剪切波变换（contourlet transform，CT）在分解与重构过程中，导致的图像平移异变、目标边界出现“振铃”现象等问题，是一种具有多尺度、多方向、平移不变性等众多优点的频率域分解方法［10-13］。傅里叶变换频率域的经典变换方法，但是只能显示图像的频率信息，无法表示频率的时间信息。针对此问题，小波变换（wavelet transform，WT）具有多分辨率、时频组合分析能力，在图像处理技术中得到了迅速的发展和广泛的应用。虽然小波变换具有良好的局部特性，但是在处理二维或者高维图像数据时，具有一定的局部限制，对图像的边界和引入的细节线状信息等都不是很好的表示，导致在融合过程中会出现虚假信息引起振铃效应。2002 年，DoM.N 提出了一种基于拉普拉斯金字塔（Laplacian pyramid，LP）结构的理论分析工具——Contourlet 变换。与小波变换相比，Contourlet 变换可以从多方向、多尺度，更好地捕获图像的边缘、纹理等信息，如图1、图2 所示。其核心思想是首先对图像进行LP 变换，获取不同分辨率的低频分量和高频分量；然后对高频分量进行多方向分解；最后将同方向的高频分量进行整合。

图1 近似和预测残差金字塔

图2 剪切波变换结构示意图

相比于小波变换，Contourlet 变换的优点在于多方向性，而且在多尺度的宽度上表现得更好。但是，由于其基本原理采用的是LP 变换，存在着下采样，因此，出现了一些图像轻微偏移、目标边界模糊、灰度值降低等问题。为了克服此类问题，Cunha A.L.等人提出了NSCT 变换方法，如图3 所示。与Contourlet 变换不同的是，NSCT 采用的是基于非下采样金字塔（non-subsampled pyramid，NSP）、非下采样方向滤波器组（non-down sampling direction filter bank，NSDFB）的方式。

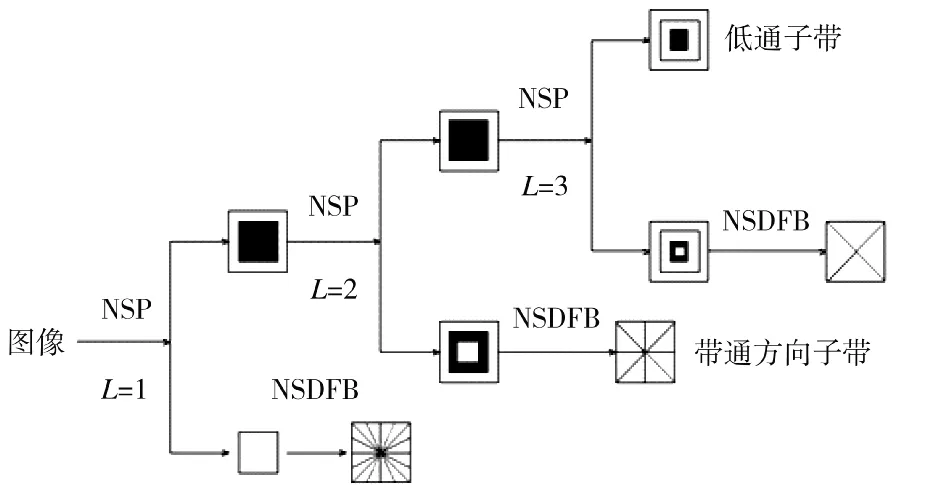
图3 非下采样轮廓波变换结构示意图

从NSCT 的结构图上来看，NSCT 采用的也是双层结构，即通过LP 变换得到低频和高频分量。不同于Contourlet 变换，NSCT 是基于上采样的变换算法：在L=1 时，对图像进行NSP 变换，使用低通和带能滤波器，得到了低频和高频子带，然后通过上采样得到了不同尺度的低频和高频信息；在L=2 时，没有对高频分量进行下采样，而是进行了NSDFB变换，以得到不同子带的图像频率信息。依此类推，通过不断对低频分量进行上采样，当对图像进行L尺度分解时：可得到一个低频子带图像IL和个方向子带，从而有效解决了平移不变性问题和由于下采样而引起的“振铃”现象。与此同时，NSCT 变换提出的滤波器组具有更加宽松的带宽选，从而在很好地保留整合图像细节、边缘等纹理信息的同时，解决了小波变换、Contourlet 变换所引发的一些问题。基于NSCT 频率域算法的一般流程是分别对红外与可见光图像进行NSCT 分解，然后对不同频率分量进行融合，最后经过NSCT 重构得到最终的融合图像，其核心在于不同频率分量的融合规则研究。比如，叶传奇提出了一种基于区域能量和区域方差的融合规则的图像融合算法；吴粉侠［4］提出了一种NSCT-PCNN 的融合算法，甄媚［5］提出了一种基于显著性的NSCT 融合算法等等。本文提出了一种对图像进行基于K-means 聚类的分割，对分割后的图像进行NSCT 变换，并基于分割图像统计信息的自适应图像融合算法。

1 K-means 聚类

聚类［8-9］就是指将具有某种相似特征的事物放在一起。在图像处理技术中，聚类主要是指将具备某种相似性或者关联性的图像数据聚集在一起，从而使相似或者关联的数据聚集，排除其他数据的目的。从聚类的目的来看，类与类之间具有聚类类别的排他性，而类内之间具有相关性。

在N个传感器图像融合技术中，给定一个图像数据集：

其中，Ij表示第j个传感器图像。聚类算法可以将图像分为K个簇，需满足：

Cm表示在N个传感器图像中的具有某种特征、属性等的第m个分类图像集。

在众多的聚类算法中，K均值聚类（K-Means），又称C均值聚类，是一种基本算法。经典的模糊C-均值聚类算法（FCM）及其各类改进算法，都是在K-means 聚类算法的基础进行演变和发展的。该算法是一种无监督的聚类算法，不需要先验知识和学习训练，能够通过自适应迭代对图像数据集进行分类。

K-means 聚类算法的核心思想是：把图像分为k个类：

其中，ijm表示在图像中的具有某种特征、属性等的第m个分类像素集，使得分类后像素集某种特征的目标函数达到最小。

K-means 聚类算法的基本流程是：

1）对第j个传感器图像Ij，选择k个聚类中心，作为迭代算法开始的初始中心点；

2）选定目标函数D，计算图像中的第j个像素点ij基于聚类中心点的目标函数Dj，并进行分类；

3）重新选择聚类中心ij+1的目标函数值Dj+1；

K-means 聚类算法通常以像素点到聚类中心的距离为目标函数，本文介绍两种常用的距离公式：

1）欧式距离（Euclidean Distance）：

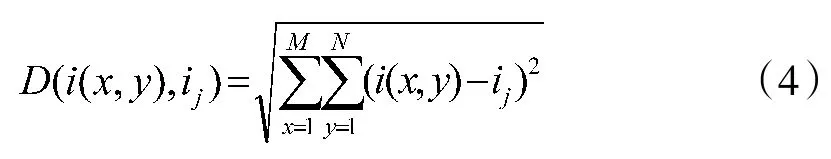
其中，M、N分别代表图像I像素矩阵的行数和列数，表示图像I的第x行，第y列像素值。

2）切比雪夫距离（Chebyshev Distance）

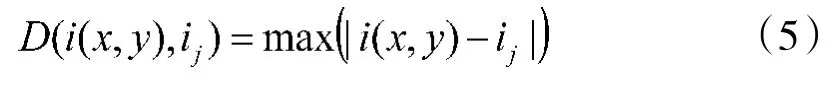
2 本文提出的算法

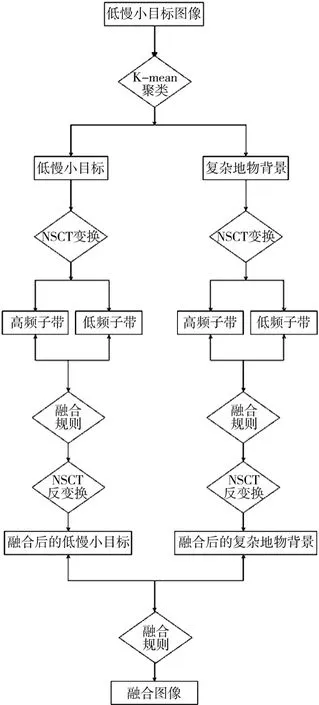
2.1 本文提出的算法流程

步骤1：采用K-means 聚类算法对红外原始图像和可见光原始图像进行2 维分割，初始点的选择为各图像的平均强度；

步骤2：对分割后的4 幅图像进行NSCT 分解；

步骤3：根据设定的融合规则，分别对同类特征的分割图像进行高频和低频融合；

步骤4：对融合后的高频和低频系数进行NSCT重构，得到融合后的分割图像；

步骤5：对2 幅融合的分割结果进行叠加，得到最终的融合图像。

2.2 K-means 聚类算法分析

经过K-means 算法分割后的图像结果，将直接影响NSCT 融合规则的选择。因此，首先对K-means算法分割的结果进行分析和评价。选择将图像分为2 类，即k=2；目标函数选为欧式距离，即式（4）；初始聚类点选择为可见光与红外原始图像的平均强度（Average Intesity）：

其中，（i，j）是像素点在图像中的位置索引；图像I的分辨率为M×N。

以经典的camp 系列图像为例，对K-means 聚类算法进行了实验和仿真。其中，图4（a）为可见光原始图像，图4（b）、图4（c）为对图4（a）进行K-means聚类分割的结果；图4（d）为红外原始图像，图4（e）、图4（f）为对图4（d）进行K-means 聚类分割的结果。表1 为利用平均强度（average intesity，AI）、平均梯度（average gradient，AG）、标准差（standard deviation，SD）、信息熵（information entropy，IE）等4 个图像质量评价指标，对图4（a）～图4（f）进行了客观指标评价，见表1 所示。

图4 camp 系列K-means 聚类分割图

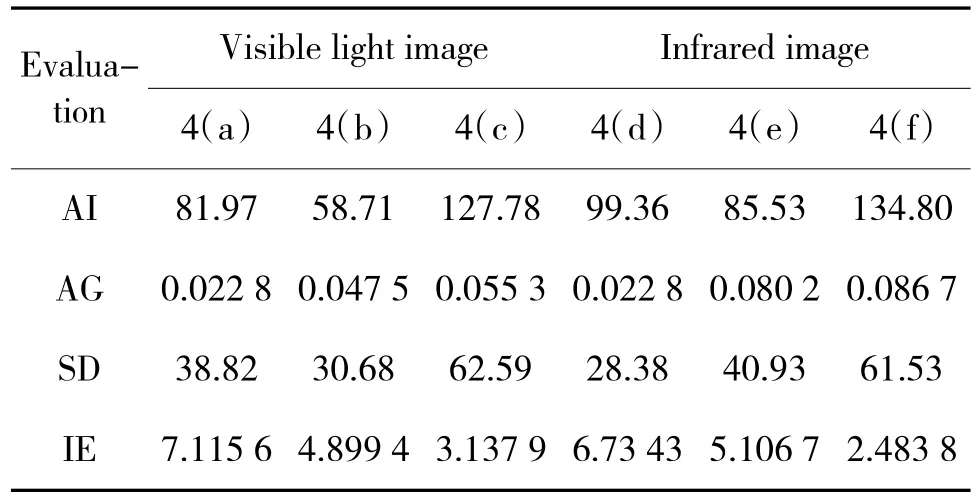
表1 camp 系列图像聚类分割图质量评价

2.3 融合规则设计

2.3.1 低频子带系数融合规则

低频子带往往反映的是图像的主要信息，低频子带图像融合为：

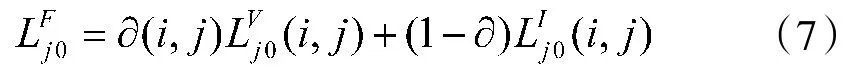
对分割结果1，由于图像的平均强度比较低，可采用加权平均法：

对分割结果2，由于图像的平均强度高，可采用取大法加大图像的整体强度：

2.3.2 高频子带系数融合规则

高频子带包含的是图像的边缘和细节信息，由表1 可知，分割后的图像仍包含图像的细节信息，可设融合规则为：

其中，

IEV为可见光图像分割的信息熵，IEI为红外图像分割的信息熵。

3 实验结果与分析

为了验证本文算法的有效性，选取了经典的camp 系列图像和tree 系列图像进行仿真实验，并且将本文的算法与其他4 种算法进行比较。

算法1：经典的空间域自适应加权平均算法，其中，融合系数取决图像的平均强度。

算法2：基于Contourlet 变换的方法。其中，方向滤波器和金字塔滤波器分别为“maxflat”和“dmaxflat7”.

算法3：基于NSCT 的方法。其中方向滤波器和金字塔滤波器分别为“maxflat”和“dmaxflat7”，低频系数融合采用加权平均法，权重取0.5；高频系数采用模值取大法。

算法4：基于NSCT 的PCNN 图像融合算法。

对于所有的多尺度算法，尺度参数设置为nlevel=［2，2，4，4］，其他设置保持一致。融合结果如图5和图6 所示。图5（a）为camp 系列红外原始图像，图5（b）为可见光原始图像，图5（c）为自适应加权融合算法处理结果，图5（d）为Contourlet 变换处理结果，图5（e）为基于NSCT 的方法处理结果，图5（f）为基于NSCT 的方法处理结果，图5（g）为本文算法处理结果。图6 为tree 系列图像处理结果。本文选用平均强度（AI）、平均梯度（AG）、标准差（SD）和信息熵（IE）作为图像质量评估指标，表2 为对图5和图6 中图像的客观质量评估结果。

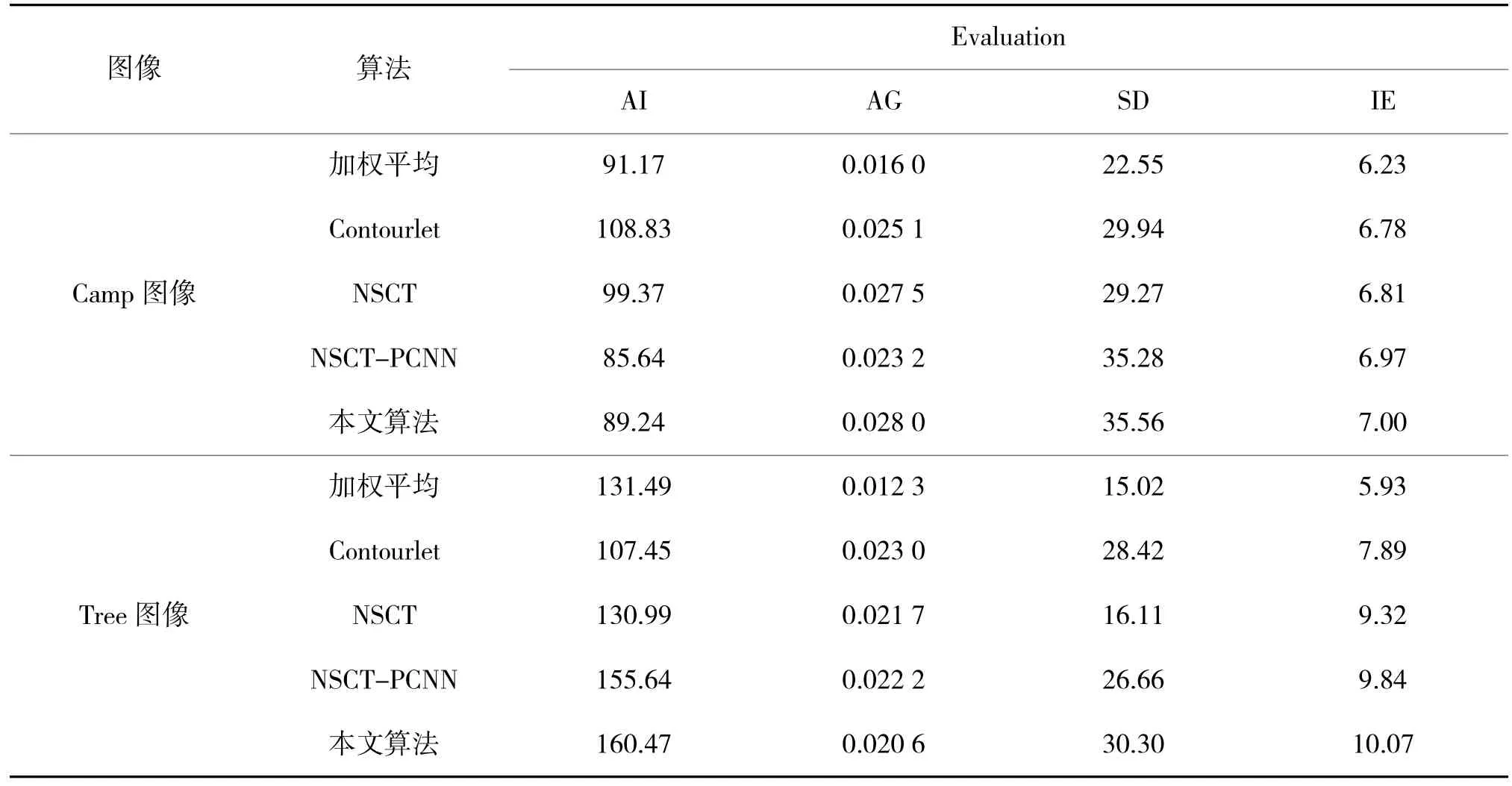
表2 实验结果的客观评价

图5 camp 系列图像的融合结果

图6 tree 系列图像的融合结果

从表1 可以看出，对于camp 系列图像来说：得出的算法在（AG）、标准差（SD）和信息熵（IE）3 个评价指标上都大于其他算法。从图像上看，图5（d）的对比度降低图像中细节成分严重丢失，模糊现象严重。图5（e）的强度最高，整体图像比较亮，但是栅栏、左下角的树木细丢失严重，图5（f）、图5（g）的细节均有所改善。相比于其他算法，本文提出的算法在栅栏、墙角、树木等细节上得到了更好的保留，可以清晰地看到栅栏与背景的区别、墙角的边缘更加清楚、树木的层次更加分明，亮度上优于NSCTPCNN 算法；对于tree 系列图像来说：本文提出的算法在平均强度（AI）、标准差（SD）和信息熵（IE）上明显优于其他算法。从图像上看最为明显，图5（d）的细节信息丢失严重，几乎看不到树木的边缘信息。图5（e）、图5（f）、图5（g）的细节信息相对有所提升。相比于其他算法，本文提出的算法在人物的细节、图像的平均强度上得到了明显的提升。

4 结论

本文提出了一种基于K-means 聚类的图像融合算法，对源图像进行聚类分割，对分割后的图像进行NSCT 变换。针对不同类的图像，对变换后的低频系数采用了不同的融合方法，对高频系数采用了基于分割图像信息熵的融合算法。最后，对融合后的系数进行NSCT 反变换得到最终的融合图像。试验结果表明，相对于经典的加权平均算法、Contourlet 变换、NSCT、NSCT-PCNN 等算法，K-means 聚类的图像融合算法具有更好的视觉效果和优秀的客观评价指标。下一步可以加强对分割聚类算法和融合规则的改进，从而达到更好的图像效果。