Multi-objective aerodynamic shape optimization of a streamlined high-speed train using Kriging model

Le ZHANG,Zhi-yuan DAI,Tian LI,Ji-ye ZHANG

State Key Laboratory of Traction Power,Southwest Jiaotong University,Chengdu 610031,China

Abstract:With continuous changes to energy-saving requirements,the task of train aerodynamic optimization becomes important.Traditional aerodynamic optimization of a high-speed train is carried out assuming the same shape of the head and tail cars,which ignores the combined effect of the two cars on aerodynamic forces.The streamlined structure of the train has different effects on the aerodynamics of the head and tail cars.In-depth study of these effects will help engineers improve their shape design capabilities.Based on the surrogate model method,this paper studies the influence of five shape parameters of the streamlined area on the resistance of the head and tail cars and the lift force of the tail car of CRH380A,and compares the aerodynamic performance of the two optimization schemes.The research results show that the optimization direction for reducing drag of the head car is opposite to that for reducing the drag and lift of the tail car,while the optimization directions for reducing both drag and lift for the tail car alone,are roughly the same.Therefore,the same shaped head and tail cars are problematic for improving aerodynamic performance.After optimization,the head car’s resistance,the tail car’s resistance,and the tail car’s lift of the train with the same shape of head and tail cars are reduced by 1.7%,0.5%,and 3.5%,respectively.The train with different shapes had values decreased by 5.6%,1.4%,and 7.5%,respectively.The optimization effect of the latter is more than twice that of the former.

Key words:High-speed train;Aerodynamic force;Optimization;Surrogate model;Streamlined area

1 Introduction

The aerodynamic drag force of a high-speed train is proportional to the square of the speed(Raghunathan et al.,2003).Drag reduction is a recurring theme of vehicle shape optimization.With the increase of speed,the lift of the tail car will also increase sharply,affecting its running stability and comfort.Baker (2010) described the nature of the flow field around the train and pointed out how the existence of that flow field led to the various aerodynamic behaviours of the train.Schetz (2001) showed,through experimental research,that when the vehicle speed reaches 300 km/h,air resistance accounts for about 80% of the total resistance.Niu et al.(2016,2018,2020,2021)studied the influence of different Reynolds numbers and different wind angles on the resistance and lift of the train,as well as the influence of different streamlined shape lengths and different braking plate layouts,on its aerodynamic characteristics.Li ZW et al.(2017)studied the aerodynamic drag of the train passing through tunnels.Li et al.(2021) investigated the influence of the gap length of double-unit trains on their resistance.Zhou et al.(2020) researched the aerodynamic performance of a high-speed maglev train.

The shape of the streamlined area of the train has the greatest influence on its aerodynamic load(Munoz-Paniagua et al.,2014a;Chen et al.,2017;Li WH et al.,2017).In order to improve the running performance of the train,scholars have attempted to optimize the shape to reduce the adverse effects of aerodynamic loads.Munoz-Paniagua et al.(2014,2015) and Munoz-Paniagua and Garcia (2019,2020)have done much research on the streamlined shape of the train,based on the surrogate model method and on the adjoint method,to reduce the total resistance of the train and the aerodynamic load under other operating conditions.Based on the Kriging model,Xu et al.(2017) and Zhang et al.(2017) conducted research to optimize the total drag force of the train and the lift of the tail car.Zhang et al.(2019) optimized the shape of the train based on two support vector regression models,with the purpose of reducing the total drag force of the train and the lift of the tail car.Yao et al.(2012,2014) used the generalized regression neural network as a surrogate model to optimize the head shape of the train so as to reduce the resistance of the whole train.They also used the Kriging model to optimize the streamlined shape,to reduce the streamline volume and the lift force on the tail car.Sun et al.(2017) optimized the shape of the train based on the Kriging model,taking the reduction of the far-field noise level and the resistance of the train as the optimization objectives.In addition to aerodynamic optimization,many scholars have done research on the aerodynamic characteristics of trains from other perspectives,and the overall conclusion is that the geometric structure of the train and surrounding facilities has a significant influence on the aerodynamic load of the train (Liu et al.,2019;Sun et al.,2019;Dong et al.,2020;Liang et al.,2020;Zou et al.,2020;Chen et al.,2021;Deng et al.,2021;Sun et al.,2021;Xia et al.,2021).The above-mentioned studies are all based on the design principle that the head car and the tail car have the same shape.Although this helps the factory to carry out standardized production and benefits train operation,it greatly limits the space for aerodynamic optimization of trains.This is because the internal connection between the structure of the streamlined area and the aerodynamics of the head and tail cars is ignored.After years of development in the field of train aerodynamic optimization,the space for improving the aerodynamic performance of trains is getting smaller because of the assumption of the same shape for the head and tail cars.

New breakthroughs in optimization are required.The shape of the streamlined area has different effects on the aerodynamic forces on the head and tail cars,and in-depth study of these will help engineers improve their shape design capabilities.After research,we found that keeping the same shape of head and tail cars is disadvantageous to the aerodynamic optimization of trains.This is because the same design variables may have opposite effects on the aerodynamic forces of the head and tail cars.Based on the surrogate model optimization method,the aerodynamic performance of a train with different head and tail car shapes is much better than that of the train where the shapes are the same.With continuous changes to train aerodynamic performance requirements,future trains might adopt autonomous adjustment technology to improve their running performance by changing their shape.Some conclusions of this paper could provide reference for future designers.

2 Tolerance fluctuation analyses

2.1 Kriging regression model

This paper adopts Kriging regression as a surrogate model.Kriging regression not only has the characteristics of easy adjustment parameters,but also has the advantages of a regression model.Compared with interpolation methods,regression methods are less susceptible to interference from sample calculation errors in the final stage of optimization.The Kriging regression model has an additional regression coefficientλ(Hoerl and Kennard,2000),andλ=1×10-6.It is determined by the leave-one-out method(Vehtari et al.,2017).ForX={x(1),x(2),…,x(n)},and their corresponding responsesy={y(1),y(2),…,y(n)},the predicted value of the Kriging regression model at the unknown pointxcan be expressed as

wherenis the total number of samples;y^ is the predicted value of the model;is the mean of the estimated value;Ψis the correlation matrix;ψis the correlation vector;Iis the identity matrix (n×n);1 is the unit column vector(n×1).

2.2 Flow field around the train

For a high-speed train running at speeds less than the Mach number of 0.3,we can regard the airflow around it as an incompressible fluid.Thus,the governing equation of the fluid around the train can be expressed as

whereuis the velocity vector,Pis the pressure,υis the coefficient of kinematic viscosity,fis the external force,andtis the time.

2.3 Non-dominated solution

Tis the set of feasible solutions for the multiobjective optimization problem.Assuming that for any two solutionsS1andS2,S1is better thanS2for all targets,then we sayS1dominatesS2.If the solution ofS1is not dominated by other solutions,thenS1is called a non-dominated solution.Its strict mathematical definition is as follows:

Consider a maximization problem with two decision vectors,S1,S2∈T.ThenS1is said to dominateS2,if:

3 Calculation model and simulation settings

3.1 Calculation model

The calculation model uses the 1:8 scale CRH380A model.We study the influence of the shape of the train’s streamlined area on the aerodynamic force.Therefore,in order to reduce the computational burden,the geometric model does not include the bogie.Although the CRH380A was in service in China as early as 2010,the disclosure of related aerodynamic experimental data in the literature only occurred much later(Han and Yao,2017;Li et al.,2021).The aerodynamic performance of CRH380A itself is already very good.It is therefore a big challenge to further optimize the train for better aero-dynamic performance.This paper attempts to do so.The characteristic heightH=0.48 m.The cross-sectional areaA=0.1687 m2.The calculation model is shown in Fig.1.

3.2 Simulation settings

The computational fluid dynamics(CFD)simulation mode is steady state.The turbulence model adopts the shear stress transport (SST)k-ωmodel (Munoz-Paniagua et al.,2017;Li et al.,2019).ABCDin Fig.1 is the velocity inlet.v(x,y,z)=(83.3,0,0)m/s.EFGHis the pressure outlet.The setting of the simulation boundary conditions is the same as that of the wind tunnel.The remaining boundaries are set as the wall.The density is 1.225 kg/m3.The solution method is pressure-velocity coupling.The second-order format is adopted for the spatial discretization of pressure.The momentum,turbulent kinetic energy,and specific dissipation rate all adopt the second-order upwind format for spatial discretization.The definitions of aerodynamic coefficient and pressure coefficient used in this study are as follows:

Fig.1 Geometric model and calculation domain

whereCdandClare the drag coefficient and lift coefficient,andFdragandFliftare the drag and lift forces,respectively.CPis the pressure coefficient,vis the train speed,andρis the density.

3.3 Grid generation and aerodynamic verification

The aerodynamic data of CRH380A is provided in (Han and Yao,2017;Li et al.,2021).Three sets of grids are used to verify the simulation results of the model (including the bogie),with the wind speed set at 60 m/s.The grid information and aerodynamic verification results are shown in Table 1.The aero-dynamic coefficients of Mesh2 are not significantly different from those of Mesh3 and of the experiment.To minimize the calculation cost,Mesh2 is selected as the meshing method.

The surrogate model method requires aerodynamic evaluation of a large number of train models,and the CFD simulation is a very time-consuming task.Bogies are at the bottom of the train,and their geometric structures are very complicated.The number of grids in this area is also very large.If we can prove that the bogie does not have a significant impact on other surfaces of the train,then the bogie can be ignored in the research process.Fig.2 is a comparison of the pressure distribution of a train with and without bogies.Fig.3 shows the position of the pressure coefficient loops and lines.Figs.4 and 5 compare the pressure coefficients of the two models.

It can be seen from Fig.2 that the most significant difference in pressure between the two models is located inside the bogie area.It has very limited impact on the flow field in other areas.Figs.4 and 5 also show that the most significant difference in the surface pressure coefficient of two models is located at the bottom of the train,but the difference is not big,and the pressure coefficient of each loop has essentially the same trend in changes with changes in angle.Many scholars have also studied the influence of the bogies.They mainly affect the flow field around themselves and the flow field near the ground under the train (Gao GJ et al.,2019;Xu et al.,2019;Guo ZJ et al.,2020;Wang et al.,2020a,2020b,2020c,2021).Therefore,we ignore the influence of the bogie structure on the flow field in the optimization process.When running at a speed of 300 km/h,the drag coefficient of the head car without bogie is 0.1337.The drag coefficient of the tail car without bogie is 0.1002 and the lift coefficient is 0.0830.

The maximum size of the car body grid is 16 mm,and the number of boundary layers is 12.The growth rate of the boundary layer is 1.2.The height of the first boundary layer is 0.01 mm.They+in most areas of the whole train is near 1.The total grid size is 19 million.The calculation grid andy+are shown in Fig.6.

Table 1 Aerodynamic verification

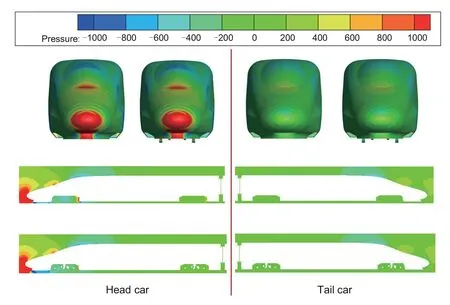
Fig.2 Pressure distribution of train with and without bogies(unit:Pa)

Fig.3 Surface pressure coefficient lines of train.X1-X6 are the locations of loops in the X direction

4 Research process and result analysis

4.1 Parametric modeling of head shape

Information on each design variable is shown in Table 2.In the parameterized model in Fig.7,the black points are the control points,the red lines are the main control lines and the blue lines are the secondary control lines.By adjusting the position of the control points on the main control line,we can change the shape of the main control line to fit the shape of the train.The coordinate of the control point on the secondary control line is adjusted linearly according to its position relative to the main control line.Ultimately,the deformation of the streamlined area of the train is achieved.

The vertical displacement of each control point onL1is controlled by

The vertical displacement of each control point onL2is controlled by

The lateral deformation of each control point onL3is controlled by

The lateral change of each control point onL4is controlled by

The vertical change of each control point onL5is controlled by

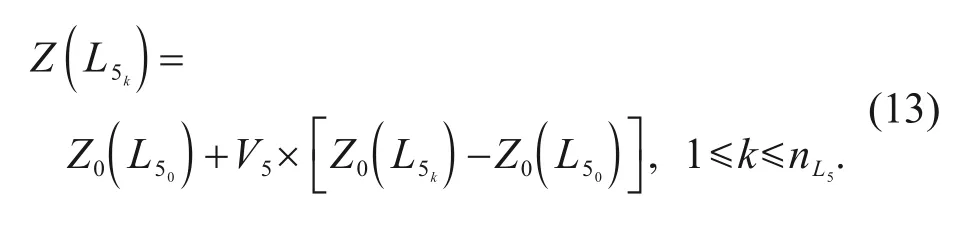
In the above equations,represents the number of control points of the control lineLj;krepresents thekth control point of the control line;Y(·)andZ(·)represent the new coordinates in the corresponding direction of the changed control point;Y0(·) andZ0(·)represent the coordinates in the corresponding direction of the control points of the original model.

Fig.4 Surface pressure coefficients of head car with and without bogies:(a)loop at X1;(b)loop at X2;(c)loop at X3;(d)loop at X4;(e)loop at X5;(f)loop at X6;(g)center line of head car;(h)bottom line of head car

The range of design variables is large,which provides a large space for train optimization.The design variables of CRH380A are:V1=0,V2=1,V3=0,V4=0,andV5=1.

4.2 Optimization process

The entire optimization process can be expressed by the following mathematical expressions:

Fig.5 Surface pressure coefficients of tail car with and without bogies:(a)loop at X1;(b)loop at X2;(c)loop at X3;(d)loop at X4;(e)loop at X5;(f)loop at X6;(g)center line of tail car;(h)bottom line of tail car

whereCdheadis the drag coefficient of the head car,Cdtailis drag coefficient of the tail car,andCltailis the lift coefficient of the tail car.

The optimization process is shown in Fig.8.Based on the Latin hypercube sampling method,we first construct 40 sample points.These sample points are the streamlined shapes of trains with different design variables.Second,we use the CFD technology to calculate the drag coefficients of the head and tail cars,and the lift coefficient of the tail car of each train.Then,we construct a surrogate model.The input of the surrogate model is the design variables of each model,and the output is the lift and drag coefficients corresponding to each model.Third,based on the existing surrogate model,we use the NSGAIII algorithm to find the Pareto solution set.Fourthly,we select some sample points from the Pareto solution set for CFD simulation,to check whether the accuracy of the surrogate model meets our requirements.If the requirements are met,the optimization is successful,and the final Pareto solution set can provide reliable data for subsequent analysis.If the requirements are not met,the simulated sample data is added to the sample set,and the surrogate model is reconstructed,until the accuracy of the model meets the requirements.

Fig.6 Grid and surface y+of the train

Table 2 Information about design variables

Fig.7 Parameterized model.References to color refer to the online version of this figure

Fig.8 Optimization process

This paper studies a three-objective optimization problem,while most train aerodynamic optimization is a two-objective optimization.So there are certain differences in the optimization process.First,there are differences in the optimization algorithm.Many scholars use the NSGAII algorithm to optimize high-speed trains,but we use the NSGAIII algorithm.The NSGAIII algorithm is an upgraded version of the former,and the difference between the two is mainly in the steps for selecting offspring.NSGAII mainly relies on the degree of crowding for sorting,which obviously does not play a significant role in a high-dimensional objective space.NSGAIII has made drastic adjustments to the crowding degree ranking,and maintains population diversity,by introducing widely distributed reference points.The number of iterations of the NSGAIII algorithm is 600,and the population size is also 600.The second difference is the strategy for adding the sample.The strategy of most scholars for adding sample points is to randomly select two from the Pareto solution set.Since the number of objectives in this paper has changed from two to three,the Pareto solution set has changed from a curve to a surface.We need to improve the point addition strategy.The extreme point of the Pareto solution set often deviates greatly from the simulation value,so seven sample points are taken from the phased Pareto solution set each time,to verify accuracy.Among them,six points are the maximum and minimum points of each objective in the Pareto solution set.The other point is randomly selected from the remaining solution set.The accuracy calculation is determined by Eq.(15),which means that the absolute value of the average relative error of the aerodynamic coefficients of the seven samples is less than 0.5%.Through iteration,the final size of the sample set is 110.

whereyiis the simulation result of the sample,which is composed of the head car drag coefficient,the tail car drag coefficient,and the tail car lift coefficient.oiis the model prediction value of the sample,which is also composed of three coefficients.yijandoijare respectively the simulated value and predicted value of thejth aerodynamic coefficient of theith sample.

4.3 Pareto solution set

After seven rounds of iteration and optimization,we obtained a Pareto solution set with higher accuracy,as shown in Fig.9.

Fig.9 Pareto solution set of three objectives.References to color refer to the online version of this figure

The green dots are the Pareto solution set,also called the non-dominated solution set.The red dot represents the aerodynamic performance of CRH380A.We noticed that the distance between the non-dominated solution set and the CRH380A aerodynamic coefficient in Euclidean space is quite close.This shows that CRH380A has excellent aerodynamic performance.By observing the shape of the Pareto solution set,we noticed an interesting phenomenon.The solutions with the smaller drag coefficients of the head car are located at the upper left of the coordinate system (inside the orange circle),but the values of both the drag and lift coefficients of the tail car are larger in this area.The area where the drag and lift coefficients of the tail car are small is located at the lower right of the coordinate system (inside the blue circle),and the drag of the head car is particularly high in this area.This indicates that in the optimization process,there is a conflict in achieving the objectives of reducing the drag of the head car,while reducing the drag force and lift force of the tail car.The related information of the head shape corresponding to the extreme values of the three objectives in the Pareto solution set is shown in Table 3 and Fig.10.

It can be seen from Table 3 that the accuracy of the surrogate model is high,which proves that the optimization results are reliable.In addition,combining Fig.10 and Table 3,it is not difficult to see that the model with the least resistance from the head car is very different from the model with the least resistance from the tail car.The model with the least drag from the tail car is also similar to the model with the least lift of the tail car.This result shows that it is difficult to ensure that all the aerodynamic forces of both the head and tail cars can be reduced to a satisfactory level if the shapes of the streamlined area of the head car and the tail car have to be kept the same.Therefore,it is necessary to further study the influence of various design variables on the resistance of the head car,the resistance of the tail car,and the lift force of the tail car.

4.4 Influence of various design variables on the aerodynamics of the head and tail cars

4.4.1 Influence of design variables on aerodynamics

We use the CRH380A as the benchmark model to further study the effects of design variables on the aerodynamics of the head and tail cars.Based on the controlled variable method,we only change the value of one of the design variables of the CRH380A each time and do six sets of simulations with different values of variables to observe the differences in the model.There are a total of 30 sets of aerodynamic results,and the influence of each design variable on the aerodynamics of the head and tail cars is shown in Fig.11.

With the increase ofV1(the driver’s cab window is more outwardly convex)the drag of the tail car and the lift of the tail car will increase,but it has little effect on the resistance of the head car.AsV2increases(the nose junction gets higher),the drag force of the tail car will first decrease and then increase slowly,while the lift of the tail car will continue to decrease.The head car’s resistance is insensitive to changes inV2.The change inV3(the horizontal control line in the upper part of the streamlined area) seems to have a very limited impact on the aerodynamics of the head car and the tail car.AsV4increases (the horizontal control line in the lower part of the streamlined area becomes more outwardly convex),the aerodynamic coefficients of the head car and the tail car increase,but the change in the resistance of the head car is very small.The change in the lift force of the tail car is the largest.With the increase ofV5(the nose becoming wider),the aerodynamic force of the head car decreases.The drag and lift of the tail car first decrease and then increase.WhenV5=1.5,the resistance and lift of the tail car reach the maximum,while the resistance of the head car is the smallest at this point.This is the main reason why the optimizations of the head and tail cars are in opposite directions.In addition,we also found that,except for slight differences inV2,the variation trends of the tail car’s resistance and the tail car’s lift related to all design variables,were basically the same,which indicated that they were largely consistent in the optimization direction.

Table 3 Information about extreme points in the Pareto solution set:design variables,aerodynamic coefficients(predicted values of surrogate models and CFD simulation values),and relative errors

Fig.10 Head shapes with the largest and smallest aerodynamic coefficients

4.4.2 Pressure and streamline distribution

We noticed thatV1andV4have a significant impact on the tail car’s lift and drag,V2has a significant impact on the tail car’s lift,andV5has a significant impact on the three aerodynamic coefficients.Therefore,we intend to analyze the cause,from the perspective of the flow field.Figs.12-16 show the influence of design variables on train aerodynamics.

AsV1increases,the curvature of the driver’s cab window of the tail car increases.When the air flow passes through the streamlined area of the tail car,the increased curvature will cause the air flow on the top of the tail car to accelerate,thereby forming a larger negative pressure.This is the main reason for the increase in the lift force.In addition,there is an angle between the window and the running direction of the train.The pulling force formed by the negative pressure on the surface of the window will produce a backward component,which will increase the resistance of the tail car.By looking at the pressure distribution in the rear view of each tail car,it can be seen that asV1increases,the negative pressure area around the window becomes larger(Fig.12).

Fig.11 Influence of design variables V1-V5(a)-(e)on the aerodynamics of the head and tail cars

Fig.12 Influence of V1 on the drag and lift forces of the tail car(unit:Pa)

Fig.13 Influence of V2 on the lift force of the tail car(unit:Pa).References to color refer to the online version of this figure

In Fig.13,we can see that change ofV2will have an impact on many positions in the streamlined area of the tail car.Although the main control line is in the nose,the secondary control line connecting the driver’s cab window and the nose must undergo corresponding linear deformation.This leads to different changes in the pressure distribution in the middle of the driver’s cab window,the end of the driver’s cab window,the end of the train’s nose,and the tip of the train’s nose.The red dotted area is the tip of the train’s nose.We noticed that with the increase ofV2,the negative pressure at the tip of the nose decreases.WhenV2=0.5,there is almost no obstruction to the process of air flow from the window of the driver’s cab to the tip of the nose,so the flow velocity is faster,resulting in negative pressure at the tip of the nose.WhenV2keeps increasing untilV2=1.5,the height of the nose end increases,which to a certain extent,blocks the airflow through the tip of the nose.Therefore,the intensity of the negative pressure also decreases.The black solid line area is the end area of the nose.The pressure change in this area is just the opposite of that at the tip of the nose.WhenV2is small,the shape of the area is concave downwards.It directly bears the impact of the airflow from the window of the driver’s cab,causing a positive pressure.WhenV2increases,the shape of the area is convex upwards,which accelerates the air flow and causes the negative pressure to increase.The black dotted area and the red solid line area are the end and middle areas of the cab window,respectively.WhenV2is small,the geometrical obstacle which airflow encounters is small,so the positive pressure at the end of the window is not large.WhenV2increases,the surface of the front part of the cab’s window is raised,hindering the air flow and resulting in an increase in positive pressure.The larger positive pressure in this area will also squeeze the area of the negative pressure zone in the middle of the window.In the red solid line box,whenV2=1.5,the negative pressure in the middle of the cab window is much smaller than whenV2=0.5.The pressure changes of the tail car caused byV2are very complicated but,in conjunction with Fig.11,we can see that the increase ofV2will cause the tail car’s lift to continue to decrease as a whole.

With the increase ofV4,the horizontal control line in the lower part of the streamlined area becomes more outwardly convex.The convexity will accelerate the airflow so,as in Fig.14,the negative pressure areas on both sides of the train gradually increase.This causes the lift of the tail car to continue to increase.The position where the dashed line intersects the sideline of the tail car is the position where the train has the greatest degree of deformation.We can use the dashed line to divide the negative pressure of the cross-section into two parts,left and right.The negative pressure zone on the left weakens the resistance of the tail car,and the negative pressure zone on the right increases the resistance.Obviously,the area of the negative pressure zone on the right is larger than that on the left,which causes the drag of the tail car to increase.This pressure distribution is mainly due to the fact that the right side of the dotted line is closer to the tip of the nose.Along the direction of the nose tip,the volume of the streamlined area decreases sharply,and a certain degree of vacuum appears when the air flows through,resulting in an increase in negative pressure.

Fig.14 Influence of V4 on tail car’s drag and lift force(unit:Pa)

Fig.15 Influence of V5 on aerodynamic forces of the head car(unit:Pa)

Among the five variables,V5is the only variable that can have a significant impact on the resistance of the head car.With the increase ofV5,the resistance of the head car is continuously reduced.From the front view of Fig.15,whenV5=0.5,the width of the nose tip of the train is narrow.Most of the area from the tip of the nose to the front of the driver’s cab window is a positive pressure zone.WhenV5=1.5,the area of the positive pressure zone at the tip of the nose is larger than that of the nose withV5=0.5.However,except for the tip of the nose,the pressure in most areas from the front of the driver’s cab window to the nose is smaller than that of the head shape withV5=0.5.Looking at the cross section (Z=106 mm),we noticed that along the direction of airflow,the positive pressure at the tip of the nose of the train withV5=1.5 decays very quickly,with the pressure at the junction of the nose becoming strongly negative.This is also because the wide nose accelerates the airflow on both sides.The intersection of the dashed line and the sideline of the train in Fig.15 is the position where the head shape changes the most.WhenV5=1.5,due to the opposite shape change trends on both sides of the dotted line,the forces generated by the negative pressure on both sides can,to a certain extent,cancel each other.WhenV5=0.5,the shape change trend on both sides of the dotted line is the same,and the force generated by the positive pressure on both sides can be regarded as running resistance.Although increasing the width of the nose increases the positive pressure area at the tip of the nose,it reduces the positive pressure in the back area of the nose.In this way,the overall aerodynamic drag of the head car can be reduced.

The increase ofV5will cause the drag force of the tail car and the tail car’s lift to first decrease and then to increase sharply.WhenV5=0.5,negative pressure appears on both sides of the tail car in the red box area in Fig.16.This is due to the vacuum effect created by the flow of air.The aerodynamic force generated by the negative pressure in this area has both a vertical component and a longitudinal component.These components become part of the drag force and lift force of the tail car.AsV5increases,the nose becomes wider and the negative pressure on both sides of the tail car in the red frame area decreases,until it disappears.This will reduce the resistance and lift of the tail car.With further increase ofV5,the negative pressure in the black frame of each tail car will increase sharply.The wider the nose,the more obvious the vacuum effect at the tip of the nose,which eventually leads to an increase in the resistance of the tail car.The protruding nose joint will accelerate the airflow,which will increase the negative pressure at the nose joint,thereby increasing the lift of the tail car.

Fig.16 Influence of V5 on aerodynamic forces of the tail car(unit:Pa).References to color refer to the online version of this figure

4.5 Comparison of aerodynamic forces of two optimization schemes

Based on the same surrogate model,two optimization schemes are designed.The shapes of the head and tail cars in Scheme 1 are different.The shapes of the head and tail cars of Scheme 2 are the same.We can compare the differences between the two optimization schemes.For Scheme 1,we refer to Table 3,to select the shapes with the least resistance of the head and tail cars respectively,because the shape with the least drag of the tail car also corresponds to a small lift.For Scheme 2,we re-do a two-objective optimization.One objective is to reduce the total resistance of the head and tail cars,and the other is to reduce the lift of the tail car.Fig.17 shows the optimized results of Scheme 2.Fig.18 shows the pressure distribution of the two schemes.

Fig.17 Pareto solution set of Scheme 2.References to color refer to the online version of this figure

The range of the abscissa in the entire Pareto chart varies from 0.230 to 0.235,indicating that the space that can be optimized in terms of drag force is very limited.Normally,the point set enclosed by the two dashed lines is an optional solution for optimization.In order to make the optimization result more obvious,we choose a solution with less resistance for simulation verification.In Fig.18,the negative pressure on the left side of the dotted line of the head car in Scheme 1 is greater than that on the right side,which reduces the resistance to a certain extent.However,there is no such phenomenon in Scheme 2.The pressure in the two positive pressure zones of the tail car in Scheme 1 is obviously greater than that in Scheme 2,which also reduces the drag and lift of the tail car of Scheme 1.Considering Table 4,no matter which metric is viewed,the optimization effect of Scheme 1 is more than twice as good as that of Scheme 2.

5 Conclusions and discussion

1.The geometric characteristics of the streamlined area shape have different effects on the aerodynamics of the head car compared with the tail car.Using the premise that the shapes of the head and tail cars remain the same,there will be many restrictions and contradictions in the aerodynamic optimization process of high-speed trains.This makes it very difficult to optimize all of the objectives(drag force of head car,tail drag,and lift force of tail car) to an optimal level.If this premise is discarded,optimization will be much better.

Fig.18 Pressure comparison of the two schemes(unit:Pa)

Table 4 Comparison of aerodynamic data and optimization results(by CFD)of the two schemes

2.The width of the nose has a great influence on the resistance of the head car,and a wider nose will reduce the resistance of the head car.However,as the nose width increases,both the drag and the lift of the tail car first decrease and then increase sharply.This leads to the optimization directions for reducing the resistance of the head and tail cars being largely opposed.

3.The two objectives of reducing the drag of the tail car and reducing the lift of the tail car have greater consistency in the optimization process.Reducing the curvature of the driver’s cab window,reducing the curvature of the lateral control line at the lower part of the streamlined area,and appropriately reducing the nose width are all helpful for reducing both the drag and lift of the tail car.Increasing the vertical height of the nose junction can also significantly reduce the lift of the tail car.

The aerodynamic shape optimization design of the train must consider not only the conventional operating conditions,but also many other factors.It is very common for trains to run in a crosswind environment,tunnel environment,or intersecting.Under these circumstances,how to adjust the shape of the head and tail of the train is still worthy of further study.

Acknowledgments

This work is supported by the National Key R&D Program of China (Nos.2020YFA0710902 and 2018YFB1201603-12),the National Natural Science Foundation of China (No.12172308),the Sichuan Provincial Science and Technology Program of China (No.2019YJ0227),and the Foundation of the State Key Laboratory of Traction Power of China (No.2019TPL_T02).

Author contributions

Le ZHANG and Zhi-yuan DAI designed the research.Le ZHANG,Zhi-yuan DAI,and Tian LI processed the corresponding data.Le ZHANG wrote the first draft of the manuscript.Ji-ye ZHANG revised and edited the final version.

Conflict of interest

Le ZHANG,Zhi-yuan DAI,Tian LI,and Ji-ye ZHANG declare that they have no conflict of interest.