A comparison study between 2D and 3D slope stability analyses considering spatial soil variability

2022-03-23LiangZHANGWenpingGONGXinxinLIXiaohuiTANChaoZHAOLeiWANG

Journal of Zhejiang University-Science A(Applied Physics & Engineering) 2022年3期

Liang ZHANG ,Wen-ping GONG✉ ,Xin-xin LI ,Xiao-hui TAN ,Chao ZHAO ,Lei WANG

1Faculty of Engineering,China University of Geosciences,Wuhan 430074,China

2School of Resources and Environmental Engineering,Hefei University of Technology,Hefei 230009,China

3Department of Civil Engineering,University of the District of Columbia,Washington DC 20008,USA

Abstract:In engineering practice,the stability of a slope is often analyzed as a 2D problem assuming a plane-strain condition,which may lead to significant errors.In this paper,a comprehensive study is carried out to compare the results of 2D and 3D slope stability analyses,using the strength reduction method for deterministic analysis and the random field approach for probabilistic analysis,respectively.The results of this comparison study confirm that in the deterministic stability evaluation,the 2D analysis tends to obtain a smaller factor of safety than does its 3D counterpart.In the probabilistic evaluation that considers the spatial variability of soil properties,the 2D analysis tends to yield a larger probability of failure than its 3D counterpart.A significant feature of the 3D probabilistic slope stability analysis is the presence of multiple local failures distributed along the slope longitudinal direction.This paper provides insights regarding the degree of errors in modeling a 3D slope as a 2D problem,which can be regarded as a complement to the previous 3D slope stability analyses.

Key words:Slope stability;Spatial variability;Probability of failure;Factor of safety;Longitudinal length

1 Introduction

Slope failure is one of the most commonly encountered geohazards around the world,which could cause significant losses of human lives and properties(Tang et al.,2019;Gong et al.,2021).The stability of a slope is often evaluated in terms of factor of safety(FS)that may be determined with either limit equilibrium methods (Spencer,1967) or numerical methods(Jin et al.,2020;Yin et al.,2021).In the routine analysis and design of a slope,the slope stability is usually analyzed as a 2D problem adopting a plane strain assumption(Abusharar and Han,2011).However,the field investigations illustrate that the failure of most realistic slopes or landslides behaves as a 3D problem,exhibiting spherical,ellipsoidal,or other complex slip surfaces(Jaboyedoff et al.,2020).There are arguments and practical reasons for adopting the 2D analysis.First,the 2D analysis is often easy to implement,as there is no need to formulate complex 3D geometries and boundary conditions.The 2D analysis is also much less computationally demanding for the same reason.Furthermore,the FS derived from the 2D analysis is generally smaller than that derived from the 3D analysis(Griffiths and Marquez,2007).As such,the 2D analysis usually leads to a more conservative slope design.

The 2D analysis may lead to significant errors in the computed FS.For example,the plane strain assumption might not be valid if the longitudinal length of a slope is not sufficiently large.The error becomes even more profound if the longitudinal variation of the slope geometry,loading conditions,or soil properties is significant.In such cases,the ‘true’ stability behavior of a slope may not be captured by the FS values of selected slope cross-sections computed with the 2D analysis.Over the past decades,the advances in computation power coupled with the recognition of the limitations and deficiencies of the 2D analysis have led to the increasing use of the 3D slope stability analysis (Griffiths et al.,2009;Hicks and Spencer,2010),and the significance of the 3D analysis has been discussed(Zhang et al.,2015).

Nevertheless,it would be of interest from the perspective of engineering practice to know the degree of errors in modeling a 3D slope as a 2D problem,which can only be assessed from a systematic comparison of the results obtained from both 2D and 3D analyses.To this end,it is noted that such a comparison of the stability analysis can be further complicated by choice of the approach,deterministic versus probabilistic.As has been well recognized,a higher FS(obtained from the deterministic approach) does not always guarantee a higher level of safety (Duncan,2000),and the slope’s probability of failure (obtained from the probabilistic approach) is also related to the uncertainty of the adopted geological model,including stratigraphic uncertainty and geo-properties uncertainty(Gong et al.,2019,2020).Thus,a comprehensive comparison of the 2D versus 3D analysis should be carried out using both deterministic and probabilistic approaches.

Although the probabilistic slope stability analysis has long been advocated (Zhou et al.,2019),most of the previous studies were based upon 2D probabilistic analyses (Griffiths et al.,2009;Hicks and Spencer,2010;Ji and Chan,2014;Hicks and Li,2018).In the earlier studies of the 3D probabilistic slope stability analysis using limit equilibrium methods,Vanmarcke(2011)compared the 2D and 3D methods for assessing the risk of long slopes(with an assumption of cylinder slip surfaces),and concluded that the 2D analysis was conservative and the occurrence of the local failures was random along the slope longitudinal direction.Ji(2014) studied the widths of the local failures for a long embankment,and concluded that the widths of the local failures were proportional to the horizontal scale of fluctuation of soil properties.In a pioneering study of the 3D probabilistic slope stability analysis using the random finite element method (RFEM),Griffiths et al.(2009) concluded that the 2D probabilistic slope stability analysis tended to overestimate the reliability index of a 3D slope.Hicks and Spencer(2010) summarized the potential failure modes of 3D slopes according to the relationship between the horizontal scale of fluctuation(of soil properties)and slope geometries.These failure modes yielded noticeable 3D features that could not be captured by the failures revealed from 2D slope stability analyses.The inconsistency in the derived reliability indexes between 2D and 3D probability slope stability analyses may be attributed to the difference in the failure modes revealed from the two approaches (Hicks et al.,2014;Hicks and Li,2018).Because of these multiple local failures,determining the reliability index of a 3D slope is more like a system reliability problem (Ji and Chan,2014).All these studies re-confirmed the significance of the 3D probabilistic slope stability analysis.With advances in computational science (Spencer,2007) and the availability of efficient sampling methods (Au and Wang,2014;Juang et al.,2017;Li et al.,2019),the practicality of 3D probabilistic slope stability analyses is gradually being enhanced.

This paper presents a comprehensive study comparing 2D and 3D slope stability analyses,in which the slope stability is evaluated with both deterministic and probabilistic approaches.It is noted that some previous studies have compared 2D and 3D slope stability analyses.For instance,Xiao et al.(2016)analyzed the relations between the FS of the 3D slope(whose soil parameters were spatially varied)and that of its cross-sections.Xiao et al.(2017)studied the 3D slope failure mechanisms and analyzed the features of local slope failures.However,the effects of the boundary conditions have not been sufficiently discussed in the previous studies,and the influence of the horizontal scale of fluctuation on the failure pattern of 3D slopes has not been sufficiently addressed.The emphasis is placed on the influences of the horizontal scale of fluctuation (of soil properties) and the longitudinal length (of the slope).Compared to the existing literature on the comparison study between 2D and 3D slope stability analyses,the new contributions of this study can be summarized as follows:(1)a more comprehensive comparison study between 2D and 3D slope stability analyses is conducted,using both deterministic and probabilistic approaches;(2) the effects of the horizontal scale of fluctuation (of soil properties) and the longitudinal length (of the slope)on the comparison are more systematically analyzed;(3)the spatial variability of both cohesion and friction angle is included in probabilistic slope stability analyses;(4) the statistics of the local slope failures (e.g.their number,width,volume,and position) in 3D probabilistic slope stability analyses are studied in a more systematic manner.

The rest of this paper is organized as follows.First,the critical components involved in this study,such as the solution model adopted for slope stability analyses and the random field modeling for soil properties,are introduced.Second,a comparison between the 2D and 3D deterministic slope stability analyses is conducted.Third,a comparison between 2D and 3D probabilistic slope stability analyses is undertaken,focusing on the influence of the horizontal scale of fluctuation and the longitudinal length.Finally,the concluding remarks are made based on the results presented.

2 Methodologies adopted for the comparative study

Neither deterministic nor probabilistic slope stability analyses are new topics.However,it should be of use to briefly review the methodologies adopted in 2D and 3D slope stability analyses herein to set the stage for the comparative study.

2.1 Deterministic solution model for slope stability analyses

The stability of a slope(either 2D or 3D)may be evaluated using either numerical or limit equilibrium approach.For explicit consideration of the spatial variability of input soil properties,the strength reductionbased numerical method (Zienkiewicz et al.,1975;Dawson et al.,1999) is adopted in this study,and the 3D explicit finite difference program FLACVersion 7.0(Itasca,2020)is selected as the solution model for evaluating the slope stability(both 2D and 3D).Within FLACVersion 7.0,the strength reduction method(Dawson et al.,1999) is employed for computing the FS,in which the shear strength of soil,in terms of its cohesion(

)and the friction angle(

),is progressively reduced (or increased) to bring the slope to a state of limiting equilibrium.With this strength reduction method,the shear strength of the soil for a trial value of FS,denoted as

(generally greater than 1.0),can be reduced as follows.

where

and

represent the reduced cohesion and friction angle,respectively.A series of FLAC simulations are made using different trial values of

until the occurrence of slope failure,and the critical trial value of

is taken as the FS of the concerned slope.Notice that in FLACVersion 7.0,the FS of a 2D slope can be easily estimated,assuming a unit longitudinal length of the slope.

2.2 Random field modeling for soil properties in slope stability analyses

In numerical modeling of a slope (either 2D or 3D),the geometrical domain of the slope is discretized into a set of small elements (or zones),thus permitting an easy assignment of different geotechnical properties to different numerical elements.It should be noted that the property within a specified element is captured by a fixed value.Thus,the property is averaged over an element domain,rather than taken at the mesh grids.They should be sampled as such,and considered in the numerical model.For illustration purposes,the stationary lognormal random field (Jiang et al.,2014;Gong et al.,2017;Qu et al.,2021) is adopted in this study to model the spatial variability of soil properties.For a lognormal random field of the soil property

with the knowledge of the mean

and the coefficient of variation (COV)

,the mean

and the standard deviation

of the equivalent normal random field ln

,are computed as follows:

The other feature of the equivalent normal field ln

is the autocorrelation structure

.In this study,the anisotropic exponential autocorrelation structure is adopted as an example and the correlation coefficient of the soil property ln

at two different positions of(

)and(

),denoted as

|,|

|),is estimated as follows:

where |

|,|

|,and |

| represent the absolute distances between the two positions of (

) and(

)along the

,and

directions,respectively;

,and

represent the scales of fluctuation of the equivalent normal field ln

along the

,and

directions,respectively.It is noted that the correlation coefficient(Eq.(3))can be decomposed into the correlation coefficients in the

,and

directions:

While the mean of the soil property ln

that is averaged over the element domain,

,is expected to be equal to that of the local soil property ln

,the standard deviation of the averaged soil property ln

,could be smaller than that of the local soil property ln

(Xiao et al.,2016).With the autocorrelation structure established in Eq.(3),the variance reduction factor of the concerned element,which ranges from 0 to 1,can be estimated according to the formulations in (Knabe et al.,1998;Huang and Griffiths,2015).Thus,the standard deviation of the averaged soil property ln

,could be readily obtained.Further,there is generally more than one random field in slope stability analyses,and these random fields are crosscorrelated.For example,both cohesion

and friction angle

of soil are characterized as random fields.In this study,the cross-correlations among the random fields are represented by a cross-correlation matrix

,which is an

matrix,and its component

is the cross-correlation coefficient between the

th random field and the

th random field(

=1,2,…,

),where

represents the number of random fields.

2.3 Sampling of the random fields of soil properties for slope stability analyses

In this study,the stepwise covariance matrix decomposition introduced by Li et al.(2019)is adopted because it is simple to implement and sufficiently accurate.In this stepwise covariance matrix decomposition,the correlation matrix of the soil property(among the numerical elements)is formulated in each and every direction separately.As a result,three correlation matrices of the soil property can be derived.They are

,and

,where the component

denotes the correlation coefficient between the soil property ln

of the

th numerical element and that of the

th numerical element in the

direction(Eq.(4b)),and the components in

and

are estimated similarly.The dimensions of

,and

are

,and

,respectively,where

,and

are the numbers of numerical elements discretized in the

,and

directions,respectively.The Cholesky decomposition of these three correlation matrices is then applied.

where

represents a lower triangular matrix andrepresents the transpose matrix of

.The crosscorrelation matrix of

can be decomposed similarly.

Based on the decomposed lower triangular matrices of

,and

,a possible sample (or realization) of the random field of the soil property

can be generated.

where

denotes the soil property that is sampled within the

th numerical element of the

thsample of the random field

(

=1,2,…,

;

=1,2,…,

),in which

denotes the number of samples of the random field and

denotes the number of discretized numerical elements (i.e.

);

and

are the mean and standard deviation of the soil property ln

that is averaged over the

th numerical element,respectively;ln

denotes the normalized soil property ln

that is sampled within the

th element of the

th sample of the random field,which is derived as follows:where ⊗denotes the Kronecker product;

is an

standard normal sample matrix (

=1,2,…,

),which may be obtained with the Latin hypercube sampling.The generated

samples of soil properties are then taken as the inputs to the built numerical model of the concerned slope.With the outcomes of the numerical analyses,the statistics of the FS and the probability of failure of the slope can be estimated through Monte Carlo simulation(MCS).

3 Comparison between 2D and 3D deterministic slope stability analyses

In this section,the boundary conditions and the mesh size settings in the numerical model for the slope stability analysis (either 2D or 3D) are discussed.Then,the results between 2D and 3D deterministic slope stability analyses are compared.The results also provide a background for comparisons between 2D and 3D probabilistic analyses.

3.1 Boundary conditions in the numerical model for slope stability analyses

In reference to a 3D slope shown in Fig.1,the slope stability is often analyzed as a 2D problem adopting a plane strain assumption;thus,the boundary condition for the stability analysis is assumed as follows:a fixed boundary is applied to the slope bottom while the roller boundary is applied to the slope back and front faces.However,the boundary condition for the 3D slope stability analysis is quite complicated.For example,three types of boundary conditions,namely,the rough-rough (RR),roughsmooth (RS),and smooth-smooth (SS) boundaries,are generally employed for the slope leftmost and rightmost faces (Griffiths and Marquez,2007).Here,the rough boundary represents the fixed boundary while the smooth boundary represents the roller boundary.Since the RS boundary is often applied to symmetric slope problems,and it is expected that the RS boundary analysis(with a slope longitudinal length of

) and the RR boundary analysis (with a slope longitudinal length of 2

)could yield the same results;this RS boundary condition is not discussed in this paper.Spencer (2007) stated that the boundary condition applied to the slope leftmost and rightmost faces exerted a vital influence on the behavior of 3D slopes,especially for short slopes(i.e.the longitudinal length is small).The difference between RR and SS boundaries in the 3D slope stability analysis may be attributed to the difference in the soil behaviors near the leftmost and rightmost faces.Thus,both RR and SS boundaries are studied in the 3D slope stability analysis.

Fig.1 Conventional 2D stability analysis of a 3D slope

To minimize the boundary effect on the FS calculation of the slope (both 2D and 3D),a sufficiently large geometric domain should be employed.However,the computational efficiency of the numerical analysis tends to decrease with the increase of the geometric domain.A parametric analysis is undertaken herein to determine the suitable geometric domain,which is captured by the dimension parameters,

,and

(Fig.1).Without loss of generality,a homogenous 3D slope with longitudinal length

of 15 m,height

of 10 m,and slope angle

of 45° is adopted in this parametric analysis.In the established numerical model,the soil behaviors are modeled with the elastic-perfectly plastic Mohr-Coulomb model,the soil properties are tabulated in Table 1,and the size of the discretized element is set at 0.5 m×0.5 m×0.5 m.Based on the results of the parametric study,the plot of which is not shown in this paper,when the values of the dimension parameters

,and

are smaller than 0.5

,the development of the potential slip surface within the slope may be interrupted by the applied boundaries;as such,the FS calculation would be affected.On the other hand,when the values of the dimension parameters

,and

are greater than 0.5

,the increase of the dimension parameters does not improve the FS calculation.Thus,the geometric domain for the slope stability analysis in this study is set as

,and

=0.5

With the aforementioned geometric domain as input,the stability of this 3D slope can readily beevaluated,adopting RR and SS boundaries,and the resulting FS values are 1.40 and 1.16,respectively.The failure modes,represented by the contour of soil displacement,of this slope derived with these two boundary conditions are shown in Figs.2a and 2b.As seen in Fig.2a,the 3D slope stability analysis with RR boundary yields a 3D failure mode,which is consistent with the 3D failure mode of the realistic landslide,the Qianjiangping landslide,described by Zhang et al.(2018).Both of the 3D slip surfaces obtained from the numerical simulation results with RR boundary and field surveys of the Qianjiangping landslide are ellipsoid-shaped.Whereas,the failure mode of the slope derived with SS boundary is consistent with that obtained from conventional 2D slope stability analyses,as illustrated in Fig.2b.Note that the 3D deterministic slope stability analysis with SS boundary and the conventional 2D slope stability analysis are theoretically identical.The SS boundary is not considered in the comparison between 2D and 3D deterministic slope stability analyses.

Table 1 Soil properties adopted in the deterministic slope stability analysis

3.2 Mesh sizes in the numerical model for slope stability analyses

It is well known that a finer mesh in the numerical model can lead to a more accurate evaluation of a geotechnical system while a coarser mesh does the opposite.Here,a parametric study is undertaken to investigate the influence of the mesh size in the FLAC model on the results of slope stability analyses.For ease of illustration,the mesh size in this study is denoted by the numbers of numerical elements discretized in the slope domain along the

,and

directions,namely,

,and

.The results of this parametric study are plotted in Fig.3.Fig.3a depicts that the resulting FS of the 3D slope,with RR boundary,decreases with the decrease of the mesh size(indicated by the increase of the number of numerical elements).Relative to the effect of the mesh size in the 2D slope cross-section (represented by

and

),the FS of the 3D slope is less sensitive to the mesh size along the longitudinal direction (represented by

).The obtained FS of the 3D slope tends to converge with the decrease of the mesh size.

Fig.2 Comparisons between two boundary conditions in 3D slope stability analyses(L=15 m,H=10 m,and θ=45°):(a)contour of nodal displacement obtained with RR boundary;(b)contour of nodal displacement obtained with SS boundary

Fig.3 Effect of the mesh size on the FS calculation of 3D slopes with RR boundary(L=15 m,H=10 m,and θ=45°):(a)calculated FS;(b)computational time

Though the decrease of the mesh size can lead to more accurate FS calculation of the slope,a finer mesh would reduce the computational efficiency.To this end,the relationship between the computational time and the mesh size adopted in the numerical model is studied,and the results are plotted in Fig.3b.Note that the calculation is conducted on a desktop computer equipped with 64 GB RAM and an AMD Ryzen Threadripper 2990WX 32-Core CPU clocked at 3.00 GHz.As can be expected,the computational time increases with the number of elements discretized in the geometric domain.As the accuracy of FS calculation also increases with the number of elements,a tradeoff relationship exists between the accuracy of FS calculation and the computational time.

As shown in Fig.3,when the mesh size adopted in the built FLAC model is set at 0.5 m×0.5 m×0.5 m(i.e.

=20,

=30,and

=20),a converged FS of this 3D slope can be obtained with RR boundary.When the mesh size is set at 1.0 m×1.0 m×1.0 m(i.e.

=10,

=15,and

=10),a compromised solution(i.e.the knee point on the tradeoff relationship) between the accuracy of the FS calculation and the computational time can be achieved.Therefore,the finer mesh (i.e.0.5 m×0.5 m×0.5 m) is adopted in the subsequent comparison using the deterministic approach.In contrast,the compromised solution of the mesh size (i.e.1.0 m×1.0 m×1.0 m) is initially selected in the comparison using the probabilistic approach.

3.3 Comparison between 2D and 3D deterministic slope stability analyses

With the adopted boundary conditions and mesh sizes,comparisons between 2D and 3D deterministic slope stability analyses can readily be conducted.In the deterministic slope stability analysis (either 2D or 3D),the soil properties are fixed values while the spatial variability of soil properties is not considered.Here,the soil properties listed in Table 1 are employed in the deterministic analysis,and the results from the 2D and 3D analyses are compared in Fig.4.

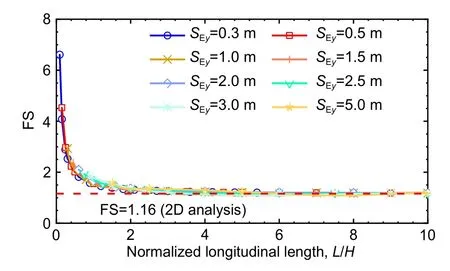
Fig.4 Comparison between the 2D and 3D deterministic slope stability analyses with RR boundary (H=10 m and θ=45°)

Fig.4 compares the FS obtained from the 3D slope stability analysis with RR boundary and those obtained from the 2D analysis.For ease of comparison,the longitudinal length

of the 3D slope is normalized by the slope height

;the term

represents the mesh size along the longitudinal direction while the mesh size in the 2D slope cross-section is set at 0.5 m×0.5 m.The plots in Fig.4 depict that the FS obtained from this 3D analysis (with RR boundary)decreases with the longitudinal length of the slope,and it tends to converge to the FS obtained from the conventional 2D analysis (i.e.FS=1.16).When the normalized longitudinal length

is greater than 5.0,the difference between the FS obtained from the 3D analysis and that obtained from the 2D analysis becomes negligible.In other words,the stability of a homogeneous slope that is sufficiently long can be accurately analyzed with the conventional 2D approach.However,the 2D analysis is likely to underestimate the FS of the short slope.Griffiths and Marquez(2007)derived a similar observation but with a stricter criterion that the normalized longitudinal length

should be larger than 10.

4 Comparison between 2D and 3D probabilistic slope stability analyses

In this section,the 2D and 3D probabilistic slope stability analyses are compared.In these comparisons,the influence of the slope longitudinal length and the horizontal scale of fluctuation of soil properties are also studied.In the 3D probabilistic slope stability analysis,both RR and SS boundaries are examined,and the mesh size is set at 1.0 m×1.0 m×1.0 m (with due consideration of the tradeoff relationship between the accuracy of FS calculation and the computational time shown in Fig.3).Table 2 summarizes the statistical properties of the soil parameters for the probabilistic analysis.

Table 2 Statistical information of soil properties adopted for the probabilistic slope stability analysis

Data from(Jiang et al.,2014)

4.1 Method adopted for estimating probabilities of failure of slopes

Although the MCS is widely utilized for sampling the random properties,it lacks efficiency,especially for problems of low probabilities of failure.As such,a hybrid approach that takes advantage of the effectiveness of the MCS in sampling the random fields of soil properties and the efficiency of moment methods in estimating the probability of failure is adopted.Here,the MCS is adopted for deriving the dimensionless moments of the performance function,and the derived moments are then utilized for estimating the probability of failure using the moment methods(Zhao and Ono,2001).First,a performance function,denoted as

,is formulated for the probabilistic slope stability analysis.

where a slope is deemed feasible (or safe) if the obtained performance function

is greater than 0 (i.e.FS＞1.0).Based on the outcome from the MCS analysis,the general statistics and dimensionless central moments of the performance function

are computed as follows:

where

and

represent the mean and the standard deviation of the performance function

,respectively;

represents the performance function value that is obtained with the

th sample of soil properties (

=1,2,…,

),in which

is the number of samples taken in the MCS;

represents the

th dimensionless central moment of the performance function

.Fig.5 illustrates the derived relationships between the central moments of the performance function

and the sample number adopted in the MCS.Fig.5 shows that the moments of the performance function

tend to converge with the increase of the number of MCS samples,and in this case,the convergence of the derived moments can be secured when the number of MCS samples exceeds 900.Hence,the number of MCS samples is set at 1000 in this study.With the aid of the derived central moments,the reliability index(

) of the concerned slope can readily be estimated with the moment method.The fourth-moment method FM-1 in (Zhao and Ono,2001) is adopted in this study.The probability of failure

is related to the estimated reliability index

as follows:

where

(·) is the cumulative distribution function(CDF)of the standard normal variable.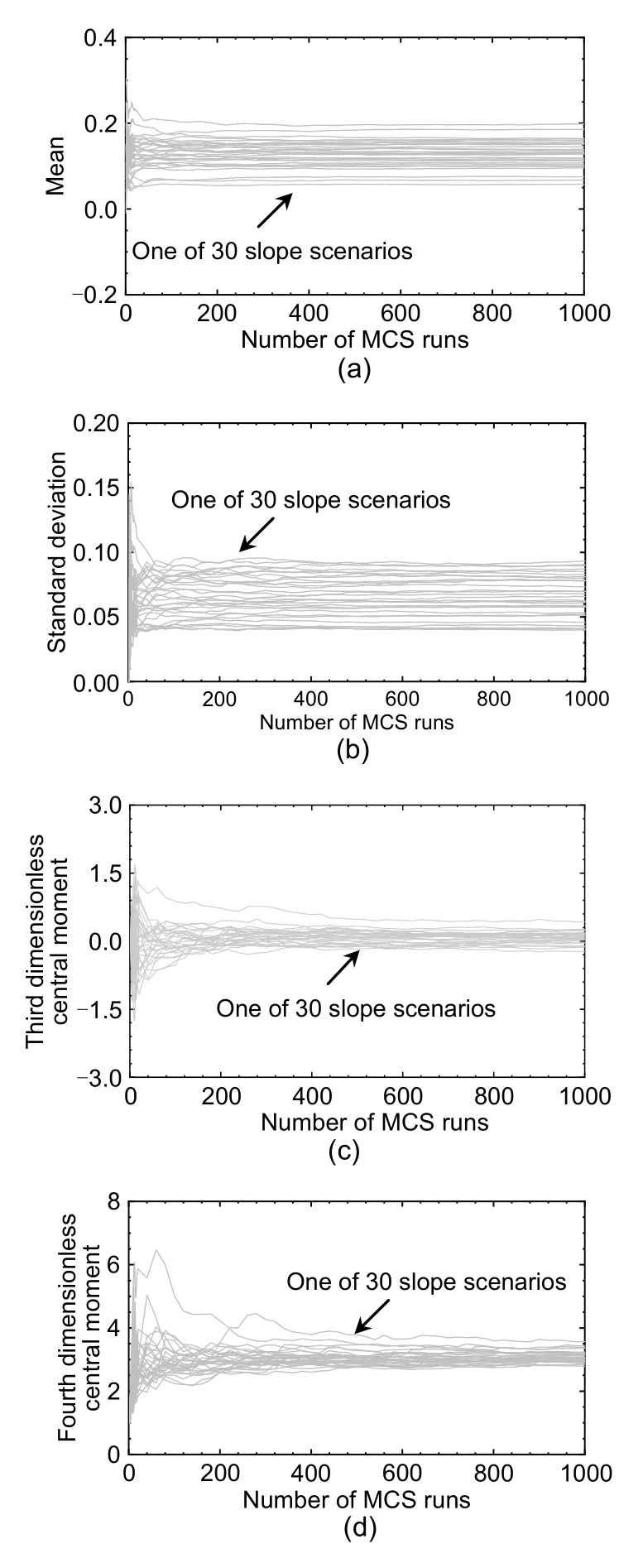

Fig.5 Convergence of the central moments of the performance function with the number of MCS runs:(a)mean;(b) standard deviation;(c) third dimensionless central moment;(d)fourth dimensionless central moment

Fig.6 validates the accuracy of the adopted fourthmoment method FM-1 in estimating the probability of failure

of the slope.In the context of the brute MCS,the COV of

,denoted as

,is approximated as follows(Ang and Tang,2007):

Fig.6 Validation of the fourth-moment method FM-1(Zhao and Ono,2001) in estimating the probability of failure of 3D slopes

With the estimated

(through counting the number of failure samples) and its COV,the 90%confidence interval of

from the MCS can be obtained with an assumption that the estimated

follows a lognormal distribution.From there,the accuracy of the adopted fourth-moment method FM-1 can be validated.For the validations shown in Figs.5 and 6,the analyses are carried out for 30 slope scenarios covering various combinations of the longitudinal lengths of the 3D slope and the horizontal scales of fluctuation of soil properties.Note that only the estimated large probabilities of failure are validated here due to the issue of computational efficiency of the brute MCS.As shown in Fig.6,the probabilities of failure from the fourth-moment method FM-1 are well bracketed by the 90%confidence intervals of the probabilities of failure from the MCS.The Pearson correlation coefficient between the

obtained from the brute MCS and that from the fourth-moment method FM-1 can also be calculated as 0.990,which implies a strong linear relation between them.Further,the emphasis of this study is on the influences of the horizontal scale of fluctuation and the longitudinal length on the estimated slope probability of failure,which might not be affected much by the improvement of the accuracy of the estimated failure probability.Thus,the validations are considered adequately performed.

4.2 Comparison between 2D and 3D probabilistic slope stability analyses

As demonstrated previously,the stability of a homogeneous slope that is sufficiently long can be studied with the 2D analysis.Two long slopes,the normalized longitudinal length

of which are set at 5 and 10,respectively,are first analyzed for the comparison between the 2D and 3D probabilistic analyses.The results that compare 2D versus 3D analyses for these two slope scenarios are presented in Fig.7,in which the vertical scale of fluctuation

is set as a constant value of 4.0 m,as commonly adopted in previous studies (Jiang et al.,2014;Li DQ et al.,2015;Xiao et al.,2016).The obtained probability of failure

generally increases with the horizontal scale of fluctuation (i.e.

) in both 2D and 3D probabilistic analyses.The trend of increase in the probability of failure may be explained by the stronger correlation and higher homogeneity of soil properties within the horizontal plane,caused by the rise of the horizontal scale of fluctuation.The influence of the horizontal scale of fluctuation is more evident in the slope longitudinal direction.Thus,the increase of the probability of failure with the horizontal scale of fluctuation is more profound in the 3D probabilistic analysis.Note that when the horizontal scale of fluctuation is sufficiently large,the probability of failure derived with the SS boundary can converge to that derived from the 2D analysis.For the two slope scenarios analyzed,the longer slope yields a higher probability of failure,as there is a greater chance of encountering a weak zone that triggers the slope failure and a longer slope tends to have more local failures along the longitudinal direction (as will be demonstrated below).This 3D nature of individual failures can be explicitly accounted for in 3D slope stability analyses.Thus,the 2D probabilistic analysis tends to overestimate the probability of failure of 3D slopes,and the degree of this error depends on the horizontal scale of fluctuation of soil properties and the slope longitudinal length.

Hicks et al.(2014)showed that it was more challenging to calibrate the horizontal scale of fluctuation of soil properties than that of the vertical scale of fluctuation.Hicks and Spencer (2010) indicated that the failure mode of a 3D slope might be influenced much more by the horizontal scale of fluctuation and the slope longitudinal length.To this end,a parametric analysis is further undertaken to address the influences of the horizontal scale of fluctuation(of soil properties)and the slope longitudinal length in the comparison of the 2D and 3D analyses.

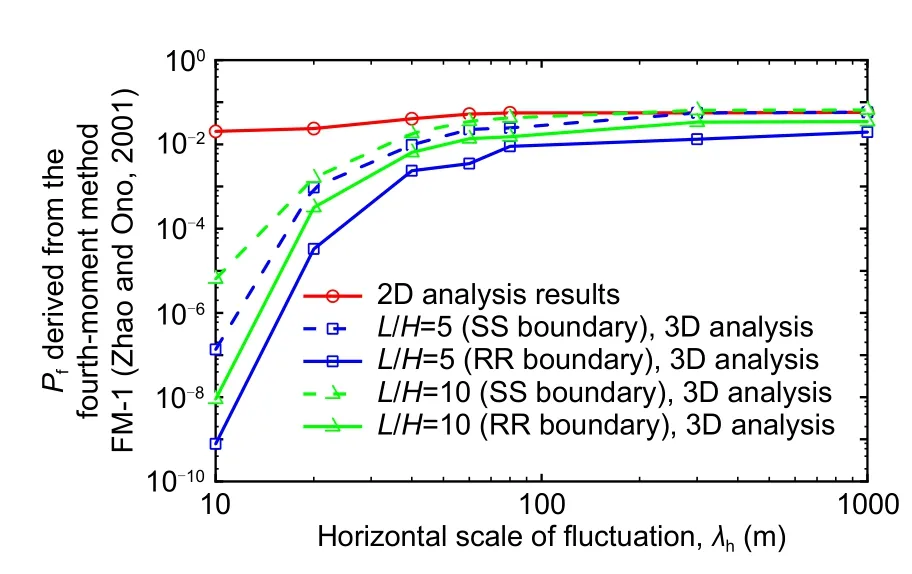
Fig.7 Effect of the horizontal scale of fluctuation of soil properties λh on the estimated probability of failure of the slope(H=10 m,θ=45°,and λv=4.0 m)

In this parametric analysis,the slope height and angle are fixed values (i.e.

=10 m and

=45°),and the vertical scale of fluctuation (of soil properties) is set as a constant value of

=4.0 m.In contrast,the horizontal scale of fluctuation and the slope longitudinal length can vary.The vertical scale of fluctuation of soil properties typically ranges from 0.1 m to 8.0 m while the horizontal scale of fluctuation ranges from 10 m to 92 m (Phoon and Kulhawy,1999;Li DQ et al.,2015).The scales of fluctuation in this parametric analysis fall well within these typical ranges.In reference to Figs.3 and 4,the results of the 3D slope stability analysis are hardly affected by the mesh size

in the slope longitudinal direction.Thus,a larger mesh size

in the slope longitudinal direction may be adopted.However,the previous study Huang and Griffiths (2015) depicted that the mesh sizes in the probabilistic slope stability analysis should be no larger than 0.25 times the scales of fluctuation.To improve the computational efficiency of this parametric analysis,the mesh size in the slope cross-section,which dominates the result of the 3D slope stability analysis,is set at 1.0 m×1.0 m.In contrast,in the longitudinal direction,it is set at 0.1

.The parametric analysis results are illustrated in Fig.8.

Fig.8 Effect of the longitudinal length on the estimated probability of failure of the 3D slope(H=10 m,θ=45°,and λv=4.0 m):(a) normalized longitudinal length L/H;(b)normalized longitudinal length L/λh

Hicks and Spencer(2010)showed that the failure mode of a 3D slope could be more influenced by the ratio of the slope longitudinal length over the horizontal scale of fluctuation,thus the slope longitudinal length in this parametric analysis is also normalized by the horizontal scale of fluctuation (

).As can be seen from Fig.8,the parametric analysis results generally agree with the observations shown in Fig.7.For example,the difference between the 2D and 3D probabilistic analysis tends to decrease with the horizontal scale of fluctuation and the slope longitudinal length.In the 3D analysis,the probability of failure obtained with the RR boundary is always smaller than that obtained with the SS boundary.The difference between the probabilities of failure obtained with these two boundaries also decreases with the horizontal scale of fluctuation and the slope longitudinal length(Fig.8b),owing to the fact that a large value of the horizontal scale of fluctuation tends to result in a large width of the local failure and a sufficient longitudinal length of the slope considerably tends to weaken the effect of the boundaries applied to the leftmost and rightmost faces.Furthermore,the probability of failure obtained from the 3D analysis is affected more by the horizontal scale of fluctuation (of soil properties),compared to its 2D counterpart.Although the 3D deterministic analysis could yield a converged stability evaluation when the slope longitudinal length is sufficiently large (e.g.

＞5.0),such a convergence cannot be reached in the 3D probabilistic analysis.For example,the probability of failure obtained from the 3D probabilistic analysis is always smaller than that obtained from its 2D counterpart,and this difference could not vanish even if a large horizontal scale of fluctuation(i.e.

=80 m) or a long slope (i.e.

=12 and

=80 m) is taken.Hence,the probability of failure for a 3D slope(either short or long)with spatially varying soil properties cannot be approximated well with the 2D probabilistic analysis;the 2D analysis tends to overestimate the probability of failure in this scenario.

4.3 Statistics of the local failures in 3D probabilistic slope stability analyses

The previous results show that in the deterministic evaluation,the stability of a homogeneous slope that is sufficiently long can be modeled as a 2D problem.In contrast,the 3D probabilistic slope stability analysis may not be approximated well with the 2D analysis.The reason behind this difference could be attributed to the multiple local slope failures distributed along the longitudinal direction of the 3D slope,which is due to the spatial variability of the soil properties.As illustrated in Fig.9,there exist multi-local failures along the longitudinal direction of a 3D slope (

=480 m and

=40 m),and the number and locations of these local failures are greatly affected by the sampled soil properties.On the other hand,only a global slope failure can be detected in the 3D deterministic slope stability analysis.As presented previously,the global failure characteristics of a 3D slope that is homogeneous and sufficiently long can be adequately captured by the 2D analysis.Thus,it is possible to estimate the FS of a 3D slope using the conventional 2D deterministic approach.

Fig.9 Multiple local failures in 3D probabilistic slope stability analyses(H=10 m,L=480 m,θ=45°,λh=40 m,and λv=4.0 m):(a)mode of one local failure;(b)mode of two local failures;(c)mode of three local failures;(d)mode of four local failures

In a numerical analysis of the slope stability using the strength reduction method,two methods are mainly adopted to automatically locate the critical slip surface(Wang et al.,2020).One is the shear strain-based approach and the other is the nodal displacement-based approach,and the latter is more extensively applied due to its simplicity.Huang et al.(2013) separated the sliding mass and the stable soil element according to the

-means clustering of the nodal displacement.Ji and Chan (2014) adopted 10% of the maximum nodal displacement as a criterion for locating the slip surface.In this study,the slip surface is derived based on the computed nodal displacement and the method presented in(Ji and Chan,2014)is adopted.The built numerical model is first discretized into a set of small numerical elements;and,if the displacement of all the nodes in a numerical element exceeds 10% of the maximum nodal displacement,this numerical element will be regarded as a sliding soil element.Then,the boundary between the sliding soil elements and the stable soil elements is taken as the slip surface.It is noted that the threshold value of 10%of the maximum nodal displacement is validated through a parametric study,in which the influences of the threshold value of the maximum nodal displacement and the FS on the located slip surfaces are investigated.In this study,the sliding direction is assumed to be perpendicular to the slope longitudinal direction,which is confirmed by the numerical simulation results.Based on the geometries of the local failures determined with this criterion,the number and the total width and volume of these local failures can be estimated.For instance,three local failures(local failure I,local failure II,and local failure III) might occur in one 3D probabilistic slope stability analysis as illustrated in Fig.10.The total width

in this simulation can be calculated as the sum of the width

,and

for local failure I,local failure II,and local failure III,respectively.The total volume

in this simulation can be similarly computed as the sum of the volume

,and

for local failure I,local failure II,and local failure III,respectively.The position

of each local failure can be defined as the ratio of the length

,which is the distance along the slope longitudinal direction from central point of the local failure to the rightmost face of the slope,to the slope longitudinal length

.Li et al.(2015) and Hicks and Li (2018) concluded that the characteristics of these local failures were mainly affected by the longitudinal length (of the slope) and the horizontal scale of fluctuation (of soil properties).A parametric analysis is conducted herein to address the influences of these factors on the characteristics of local slope failures.The results of this parametric study,which cover the number of local failures,the total width,and the total volume,are discussed below.

Fig.10 Estimate of the characteristics of local slope failures in 3D slope stability analyses

As shown in Fig.11,multiple local failures can be observed in many 3D slope scenarios;however,the single failure mode has the highest frequency,which is in good agreement with the findings of Li YJ et al.(2015).Fig.11a shows that the number of local failures is strongly affected by the slope longitudinal length (with either RR or SS boundary).For example,when the horizontal scale of fluctuation(of soil properties)is a fixed value(e.g.

=40 m),the increase in the slope longitudinal length leads to a decrease in the frequency of the single failure mode and an increase in the incidence of multiple failures.In other words,a larger slope longitudinal length tends to yield more local failures in the 3D probabilistic slope stability analysis (because of a greater chance of encountering a weak zone that triggers the slope failure),providing a convincing reason for the increase of the probability of failure as the slope longitudinal length increases.Compared with the longitudinal length,the number of local failures within the 3D slope is less influenced by the horizontal scale of fluctuation,as shown in Fig.11b.Note that a higher value of the horizontal scale of fluctuation decreases the incidence of multiple failures (Hicks and Li,2018).When the slope longitudinal length and the horizontal scale of fluctuation are proportionally increased (e.g.

=12),the similar trend of the number of local failures (with either RR or SS boundary) can be obtained,which implies the influence of the slope longitudinal length on the incidence of local failures covers that of the horizontal scale of fluctuation.

Fig.11 Effect of input parameters on the number of local failures(H=10 m,θ=45°,and λv=4.0 m):(a)λh=40 m;(b)L/λh=12

To remove the influence of the longitudinal length,we normalize the total width and total volume of the local slope failures with the slope longitudinal length.Fig.12 shows the influence of the slope longitudinal length and the horizontal scale of fluctuation on the normalized total width of local failures.The mean of the normalized total width of the local failures decreases with the slope longitudinal length(at a specified horizontal scale of fluctuation of soil properties)and the horizontal scale of fluctuation.On the other hand,the COV of the normalized total width of the local failures increases with the slope longitudinal length and the horizontal scale of fluctuation.Furthermore,as the geometry of the 2D slope cross-section is fixed in this parametric study,the effects of the slope longitudinal length and the horizontal scale of fluctuation on the normalized total volume of the local failures are similar to those on the normalized total width.

The mean of the normalized total width and that of the normalized total volume obtained with the RR boundary are both larger than those obtained with the SS boundary.In contrast,the COVs of the normalized total width and the normalized total volume obtained with the RR boundary are smaller than those obtained with the SS boundary.The different behaviors of the statistics of the normalized total width and the normalized total volume may be attributed to the fact that the local slope failures close to the leftmost and rightmost boundaries are constrained by the stricter RR boundary,as illustrated in Fig.13.The frequency for the local failures close to the leftmost and rightmost boundaries is less than that obtained with the SS boundary,which provides another reason for the larger probabilities of failure obtained with the SS boundary(in comparison to those obtained with the RR boundary).Similar results with different scales of fluctuation of Fig.13 can be also obtained,which indicate that the influence of the boundaries on the distribution of the local failures is not affected much by the scales of fluctuation.The relatively uniform distribution of the local failures along the longitudinal direction shown in Fig.13 indicates that the occurrence of the local failures is random along the slope longitudinal direction(Vanmarcke,2011),revealing the complexity of the 3D probabilistic slope stability analysis.

Fig.12 Effect of input parameters on the statistics of the normalized total width (b/L) of local failures (H=10 m, θ=45°,and λv=4.0 m):(a)mean of the total width;(b)COV of the total width

Fig.13 Histograms for the positions of local failures along the longitudinal direction(H=10 m,L=480 m,θ=45°,and λv=4.0 m,λh=40 m):(a)RR boundary;(b)SS boundary

5 Conclusions

This paper presented a comprehensive study to compare 2D and 3D slope stability analyses,using both deterministic and probabilistic approaches.In the deterministic evaluation,the soil properties were simulated as fixed values,and the primary purpose was to examine the suitability of the conventional 2D slope stability analysis in a 3D slope problem.In the probabilistic evaluation,the spatial variability of soil properties was explicitly considered,while the emphasis was on the impact of the longitudinal length (of the 3D slope) and the horizontal scale of fluctuation(of soil properties) when comparing the 2D analysis with the 3D analysis.The occurrence and effect of multiple local failures in the 3D probabilistic slope stability analysis were also examined.Based on the results presented,the following conclusions were reached.

1.In light of the 3D failure mode of real slopes or landslides observed in the field,the RR boundary was judged most suitable for a strict 3D slope stability analysis.In contrast,the 3D analysis with the SS boundary should be viewed only as an extension of the conventional 2D analysis.In the deterministic evaluation,the results showed that the FS of a long homogeneous slope(i.e.

＞5.0)could be accurately analyzed with the conventional 2D analysis.For shorter slopes,the 2D analysis generally underestimated the FS.

2.In the probabilistic evaluation,the 3D analysis generally yielded a probability of failure smaller than that obtained from its 2D counterpart.The difference in the computed probabilities of failure,between 2D and 3D analyses,decreased with the slope longitudinal length and the horizontal scale of fluctuation (of soil properties).The probability of failure obtained from the 3D analysis was more sensitive to the horizontal scale of fluctuation than did its 2D counterpart.In the face of the spatial variability of soil properties,the probability of failure for a 3D slope (either short or long) cannot be approximated with the conventional 2D analysis.Indeed,the 2D analysis generally overestimated the probability of failure in such scenarios.Furthermore,in the context of the 3D probabilistic slope stability analysis,the probability of failure obtained with the RR boundary was found to be smaller than that obtained with the SS boundary.

3.The multiple local failures distributed along the slope longitudinal direction (caused by the existence of the weak zones) were found to be a factor that could explain the difference in the computed failure probabilities between 2D and 3D analyses.Although multiple local slope failures were found in many 3D slope scenarios,the single failure mode was still the most likely scenario.The number of local failures was found to be less influenced by the horizontal scale of fluctuation than by the longitudinal length of the slope.The mean values of the normalized total width and the normalized total volume (of local slope failures) decreased with the slope longitudinal length and the horizontal scale of fluctuation.At the same time,their COVs generally increased with the slope longitudinal length and the horizontal scale of fluctuation.The mean values of the normalized total width and the normalized total volume(of local slope failures) obtained with the RR boundary were greater than those obtained with the SS boundary,while their COVs obtained with the RR boundary were smaller than those obtained with the SS boundary.

Acknowledgments

This work is supported by the Major Program of National Natural Science Foundation of China (No.42090055),the National Natural Science Foundation of China (No.41977242),and the Fundamental Research Funds for the Central Universities,China(No.CUGGC09).

Author contributions

Liang ZHANG:methodology,data curation,investigation,formal analysis,writing-original draft,visualization.Wen-ping GONG:conceptualization,writing-original draft,formal analysis,writing-review &editing.Xin-xin LI:investigation,writing-review &editing.Xiao-hui TAN:investigation,writingreview &editing.Chao ZHAO:investigation,visualization.Lei WANG:investigation,writing-review&editing.

Conflict of interest

Liang ZHANG,Wen-ping GONG,Xin-xin LI,Xiao-hui TAN,Chao ZHAO,and Lei WANG declare that they have no conflict of interest.

Journal of Zhejiang University-Science A(Applied Physics & Engineering)

2022年3期