中职学生数学核心素养现状实证研究——以福建省晋江市晋兴职业中专学校为例

吴顺英

中职学生数学核心素养现状实证研究——以福建省晋江市晋兴职业中专学校为例

吴顺英

（晋江市晋兴职业中专学校，福建 晋江 362214）

本文通过对福建省晋江市晋兴职业中专学校学生进行调查分析，发现中职学生存在初有兴趣，学有余力，重视理论，轻视实践和核心素养发展不均的问题。针对以上问题，提出了立足学生现状，设定教学课程、基于专业特色，创新教学内容、建立合理机制，完善教学考核、利用信息技术，革新教学手段的建议。

中职学生；数学核心素养；现状；对策

一、引言

“核心素养”这一名词，最早由OECD（经济合作与发展组织）提出，后经一些组织或国家纷纷提出并完善，数学核心素养则是学生在学习中逐步形成的，是数学在学生身上的一种文化体现。核心素养是其他素养中最根本的素养，同时，也成为日后生活与工作中数学素养水平的一种内在表现形式。目前，国内外对于核心素养的研究主要分为概念界定和教学策略两类，史宁中[1]，张奠宙[2]，章建跃[3]，任子朝[4]，朱立明[5]等学者从普通高中的核心素养进行研究。

2020年1月，教育部职成司发布《中等职业学校数学课程标准》（简称“中职数学课程标准”），这是我国历史上第一部中职数学课程标准[6]。而关于核心素养这一部分则是参考《高中数学课程标准》所确定的，分为六大核心素养，并从三个方面对其进行界定。

因此，考查中职学生核心素养的现状，并且通过何种方式提高学生核心素养，就成为当下绕不开的热点话题。本文基于此背景，通过对福建省晋江市晋兴职业中专学校学生进行调查研究，运用多元回归分析对该校学生的数学学科核心素养进行综合考查，进一步确定中职学生在核心素养这一背景评价下的现状。进而有助于教师更为精确地对学生进行教学与指导，做到因材施教，为改善核心素养发展不平衡这一现状提出相关建议。

二、数据分析

（一）研究对象

本文采用分层抽样的方法，选取晋江市晋兴职业中专学校中职学生320名。采取集中发放，共收回问卷320份，经剔除无效问卷后，剩余有效问卷300份。在此样本中，男生共158名，占总人数的52.7%，女生共142名，占总人数的47.3%。结合中职学校的男女比例，初步可推断该调查所抽取样本具有代表性。

（二）统计分析

1.描述性统计

如样本描述性统计表（表1）所示，总的来看，中职学生对于数学呈现出“初有兴趣，学有余力”的现状。具体而言，从排名来看，班级总体排名在前的同学，数学也与其总排名吻合；从教学模式上看，学生更偏向于利用信息技术进行教学，不喜欢自主探讨新知，这与学生的年龄特征和其自身的基础也有着一定的关系，即中职学生存在学习能力弱，学习效率低等现象；从学生对数学的自信程度来看，大部分学生对数学并不自信，这需要教师对学生进行培养与鼓励，以促进学生可以得到更好的发展。

表1 样本描述性统计表

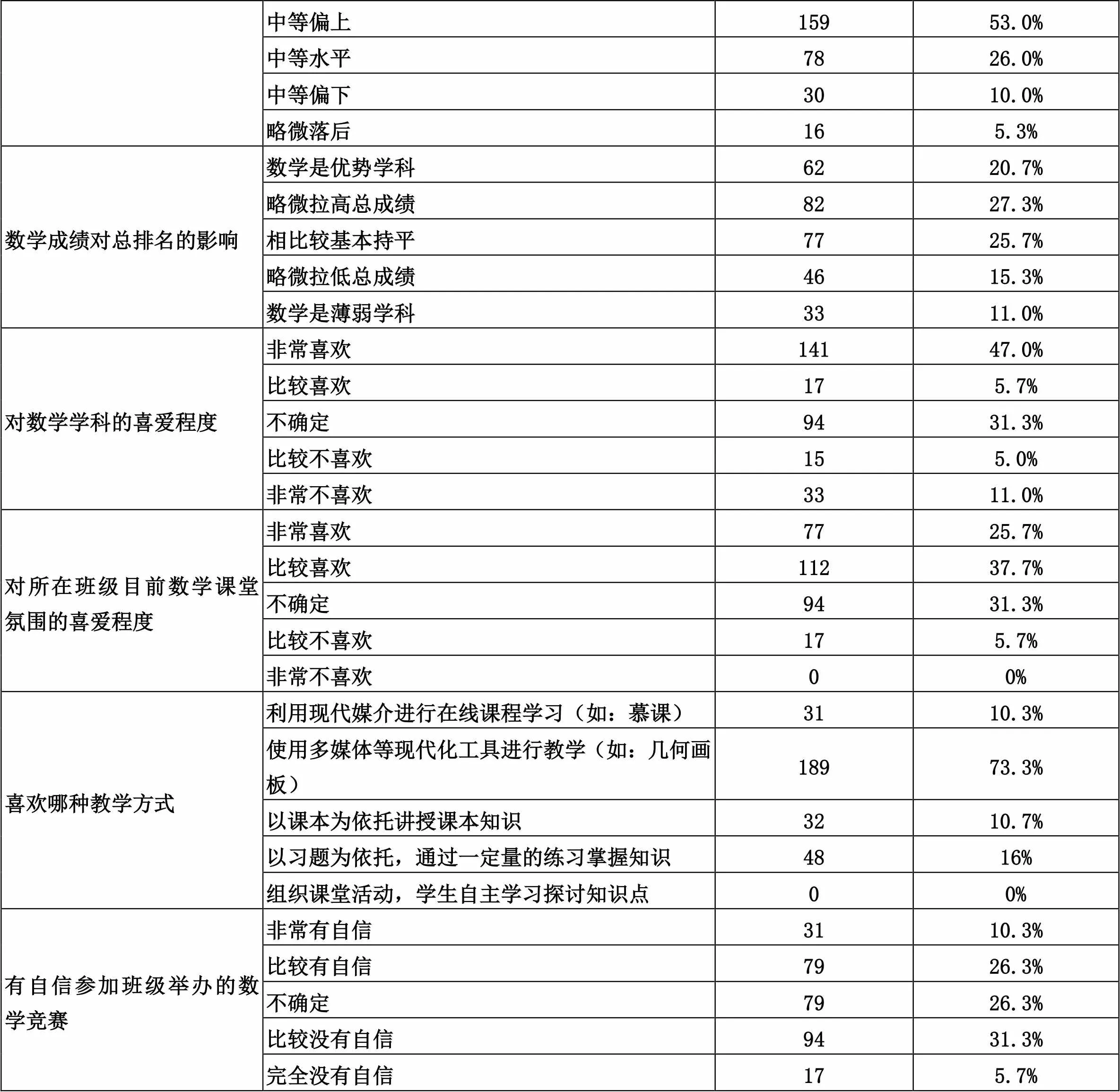
中等偏上15953.0% 中等水平7826.0% 中等偏下3010.0% 略微落后165.3% 数学成绩对总排名的影响数学是优势学科6220.7% 略微拉高总成绩8227.3% 相比较基本持平7725.7% 略微拉低总成绩4615.3% 数学是薄弱学科3311.0% 对数学学科的喜爱程度非常喜欢14147.0% 比较喜欢175.7% 不确定9431.3% 比较不喜欢155.0% 非常不喜欢3311.0% 对所在班级目前数学课堂氛围的喜爱程度非常喜欢7725.7% 比较喜欢11237.7% 不确定9431.3% 比较不喜欢175.7% 非常不喜欢00% 喜欢哪种教学方式利用现代媒介进行在线课程学习（如：慕课）3110.3% 使用多媒体等现代化工具进行教学（如：几何画板）18973.3% 以课本为依托讲授课本知识3210.7% 以习题为依托，通过一定量的练习掌握知识4816% 组织课堂活动，学生自主学习探讨知识点00% 有自信参加班级举办的数学竞赛非常有自信3110.3% 比较有自信7926.3% 不确定7926.3% 比较没有自信9431.3% 完全没有自信175.7%

2.数学基本素养分析

现如今，对数学基本素养的考查，可谓是五花八门，这里通过几道基础题对学生进行考查，问题各有侧重，可从一定程度上反馈学生的基本素养。

问题1：为什么认为0是自然数？

认为“0具有自然数的性质”共有174人，占比58%；认为“0是测量的起点”共有15人，占比5%；认为“为了使自然数能表示空集的基数”共有46人，占比15.3%；认为“0是数轴的原点”共有65人，占比21.7%。这里采取自然数的序数性这一基本功能，并结合集合相关知识，确定标准答案为“为了使自然数能表示空集的基数”即正确率为15.3%。仿照上述过程，给出其余试题和答案及学生正确选项比重。

问题2：对数的发明者是？纳皮尔，正确率32%；问题3：最早把“圆周率”计算精确到3.1415926到3.1415927之间的人是？祖冲之，正确率78.7%；问题4：勾股定理在中国最早记载在？《周髀算经》，正确率41.7%；问题5：数学领域最高奖项？菲尔兹奖，正确率37%。

综上分析得出结论，学生对于基本数学知识略有掌握，但对于专业性强，知识相似度高，涉及领域宽的知识便显得手足无措。这就要求教师在授课时，要以问题导学为先，以讲授为主，以讨论为辅的教学手段，促进学生更好地融入课堂，掌握新知；其次，在课堂上，要以实际情景等趣味知识为主，从而推进学生高质量的学习与深层次的感悟，做到一体两翼，创新发展；最后，教师要积极组织学生进行数学史，数学思想，数学方法的讨论，分享学习中的心得体会，做到多层次，跨学科，全方位发展。

3.数学核心素养影响要素

数学核心素养共六个方面，而对于学生的考查则较难从单一的方向进行评估，笔者综合前人的研究，从其普及情况，模块掌握情况，数学文化，素养能力共四方面进行比较，进一步可以深入探究对于核心素养的影响要素，为下文分析打下基础。

第一，核心素养概念普及较全面。经问卷统计可知，有36.7%的学生对于核心素养有过深入学习，41.7%的学生了解但不深入，有11%的学生稍有了解，10.7%的学生并不了解。这说明，学生对于核心素养有了初步认识，这便需要教师在教学中，潜移默化地辅助学生提升核心素养，提高能力。

第二，各模块学生掌握情况呈现“学易弃难”的局面。通过调查研究，得到学生掌握模块的情况，有43%的学生掌握“基础知识”模块的知识，而“函数”模块的掌握情况是27%，对于其他知识点则呈现顺次递减的趋势，这表明，学生对基础知识可接受，而对于较难的知识点仍然存在畏难情绪。此时便需要教师及时掌握学生动向，对于学生较难掌握，较难理解的知识点，要及时予以指导，深入浅出地教学，才能对学生的学习起到事半功倍的效果。

第三，学生数学文化认同度强，人生观与价值观正确。由于数学文化涵盖方方面面的内容，这里仅选取学生对于数学美学价值方面的认识和含有课程思政方向的价值观进行探讨。在研究中，学生对于数学的美学价值（简洁美、结构美、语言美、质朴美、统一美）并不统一，但大体上认为其“简洁美”和“结构美”为主，对关于数学所能培养的价值观而言，学生则普遍认为可以培养“爱国主义”“开拓创新”和“坚韧不拔”的精神。这也与新时代下的中职数学课程标准的课程任务是相通的，即通过学习必备的数学知识与技能，掌握一定的方法和能力，提高发现并解决问题的意识，形成科学与工匠精神，增强有助于社会发展的创新能力，最终成为全面发展的高素质劳动者和技术技能人才。

第四，学生现阶段的短板与不足。

通过对“教师上课讲授时所注重的内容”以及“学生希望学到的知识与能力”进行统计分析，发现教师注重数学基础知识，解题技巧和逻辑推理能力三方面，这正是数学教师所共同的特征，即“重基础，重解题，重方法”，反观学生，则更希望提升逻辑思维能力，将实际问题转化为数学模型的能力以及空间想象能力，这正是学生所缺失的能力，即“强理论，弱应用”“强直观，弱逻辑”和“强计算，弱空间”的现状。因此，这是建立学生核心素养的新方向与新抓手，从理论与实际相结合出发，以实际生活情景入手，充分调动学生的课堂积极性和课后钻研精神，增加自主学习时间，提高自主学习兴趣，进而有效提升学科核心素养的发展。

（三）回归分析

上文从基本情况、数学基本素养和影响核心素养要素三方面进行探究，初步形成结论，下文通过对核心素养的具体分解，以学生学习成绩为因变量，探究核心素养对学生成绩的影响。

1.指标选择

《中职数学课程标准》[7]中确定中等职业学校数学学科核心素养为数学运算、直观想象、逻辑推理、数学抽象、数据分析和数学建模，共六部分。但由于上述六部分过于抽象，笔者结合前人分析，将六部分进行如下分解：数学运算分解成数学计算能力、数学变换能力和数学解题能力；直观想象分解成空间想象能力和感知形态与变化的能力；逻辑推理分解成演绎推理能力和合情推理能力；数学抽象分解成数学抽象能力和数学概括能力；数据分析分解成数据处理能力和数学阅读能力；数学建模分解成数学建模能力、数学交流能力和数学应用能力。

虽然对核心素养进行分解诠释，但其中每一部分仍能体现其核心素养能力。如：数学计算能力仍能体现数学运算这一核心素养。

2.数据分析

本研究采用SPSS 26.0软件对现有数据进行多元回归分析，将上述六大核心素养所分解的14种能力作为自变量输入，以学生数学成绩排名作为因变量，得到能力影响系数表（见表3），其中，剔除无关要素，剩余五项构成影响成绩的核心素养分支。

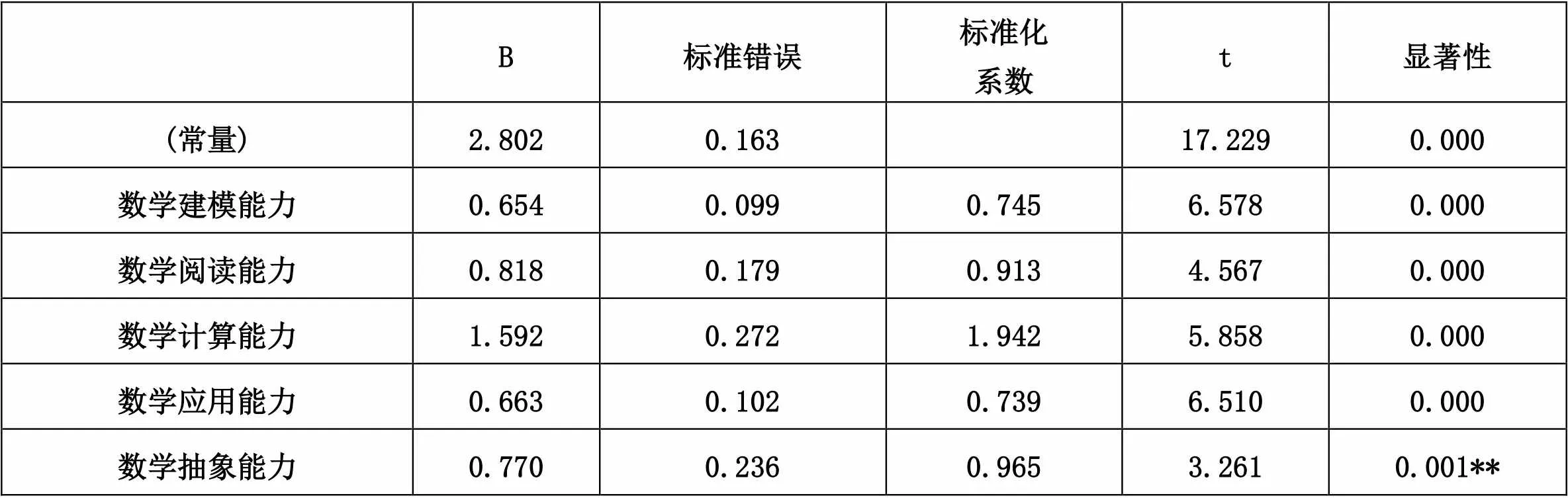
表2 能力影响系数表

注：因变量为学生数学成绩排名

3.模型构建

根据多元回归分析可得如下标准化回归模型：

Y=0.745*数学建模+0.913*数据分析+1.942*数学运算+0.739*数学应用+0.965*数学抽象

4.模型解释

学生数学成绩排名与数学建模、数据分析、数学运算、数学应用和数学抽象的五个解释变量的标准相关系数依次为0.745、0.913、1.942、0.739和0.965，这就意味着，数学运算对于学生数学成绩起着至关重要的作用，其次，通过数学抽象，将实际性问题转变为数学问题也是不可小觑的重要因素，第三，随着大数据时代的到来，数据分析成为一项重要技能，核心素养中提出数据分析，也是将数学从理论层面应用于实践层面的重要表现。

三、结论与建议

（一）结论

通过对该校300名中职学生的调查与分析，并从多个角度进行探究与挖掘，得到如下结论：

总体来说，当前学生对于核心素养处于初步了解阶段，并未从根本上达到核心素养所要求的层次，仍需更深化教育与培养，在潜移默化中培养中职学生数学核心素养能力。具体而言，呈现以下三方面的情况：

第一，初有兴趣，学有余力。中职学生在义务教育阶段，由于某些原因导致这一群体普遍存在基础弱，学习能力偏低，自主学习时间短，缺乏自信心等不良现状，但随着年龄的增长，青春期的转变，越来越多的学生开始意识到学习的重要并逐步产生较为浓厚的学习兴趣。大部分学生都希望可以在中职学校学到知识与技术，为未来的进一步深造和就业奠定基础。因此，这也就是为什么即使学生对于数学有兴趣，但是仍然成绩较低的原因。

第二，重视理论，轻视实践。目前，职业教育在我国依旧是不可忽视的话题，通过本次调查研究发现，中职学校对于学生的培养与要求，仍偏向于理论知识，教师教授课程以基础知识、解题技能等方法为主，但是反观学生更希望提升逻辑思维能力，将实际问题转化为数学模型的能力以及空间想象能力，这也正是现如今学生所缺失的能力。换言之，如何将学生所学的数学知识更好地用于今后的实习与工作之中，如何将数学与专业紧密结合，如何通过核心素养的培养使得学生具备从业，就业，创业等与时俱进的能力，仍是目前需要多方努力才能解决的一个重要问题。

第三，核心素养发展不均。通过建立标准化模型，即得到学生成绩=0.745*数学建模+0.913*数据分析+1.942*数学运算+0.739*数学应用+0.965*数学抽象，也就代表数学运算这一核心素养对学生成绩起着关键性的作用，但是核心素养的本质应该是协同发展、共同提升的，不难认为现如今其他核心素养在影响学生成绩层面上较为薄弱，例如，数学建模方面，本质上数学建模应该是考查学生对于实际问题中的因素进行简化、抽象、求解和验证并解决实际问题的能力。但在实际考察中，仅仅是应用题进行考察，学生核心素养无法得到全面发展，才会造成数学运算素养强的学生成绩也高的局面。

（二）建议

1.立足学生现状，设定教学课程

从教学课程上看，学生自身的学习热情是存在的，这就需要教师抓住学生的学习热情，立足学生现状，通过设定符合学生自身发展的教学课程，循序渐进的教学指导，进而使得学生能够发展其自身核心素养，建立起完备的素养观念。

2.基于专业特色，创新教学内容

从教学内容上来说，学生存在着觉得所学知识无用，学不到真本领的想法，这就需要教师进行引导，通过对学生今后想发展的专业领域进行讲授，如机电机械相关专业，教师应更深入地培养学生直观想象的素养，识图看图作图的能力，而对于会计相关专业，教师则更应培养数学运算、数据分析的素养，培养学生建立起对数字的敏感性，有的放矢因材施教地去培养学生。

3.利用信息技术，革新教学手段

随着时代的发展，社会的进步，信息化已成为当今的主流趋势，课堂中很难通过“粉笔—黑板”的这一传统教学模式吸引学生，又因为数学这一特殊学科，有效利用信息技术软件在教学中会起到事半功倍的效果。

4.建立合理机制，完善教学考核

中职教育，从其本质上说应是一种职业教育。因此，在对于学生的考核时，就不能全盘使用理论考核，更多的应该是理论与实际相结合的考核方式，教师需通过素质教育提升学生的实际技能，让学生有目标，有方向，有信心，进而成为社会岗位需要的实用型人才。

[1]刘祖希.访史宁中教授:谈数学基本思想、数学核心素养等问题[J].数学通报,2017,56(5):1-5.

[2]洪燕君,周九诗,王尚志等.《普通高中数学课程标准(修订稿)》的意见征询——访谈张奠宙先生[J].数学教育学报,2015,24(3):35-39.

[3]章建跃.高中数学教材落实核心素养的几点思考[J].课程·教材·教法,2016,36(7):44-49.

[4]任子朝,陈昂,赵轩.数学核心素养评价研究[J].课程·教材·教法,2018,38(5):116-121.

[5]朱立明.高中生数学学科核心素养:内涵、价值与特质[J].教育科学研究,2020(7):79-83.

[6]秦静,毕渔民.引领中职数学学科发展的课程标准研究——《中等职业学校数学课程标准》解读[J].中国职业技术教育,2020(20):5-8.

[7]教育部.中等职业学校数学课程标准[M].北京:高等教育出版社,2020.

吴顺英（1982—），女，汉族，福建晋江人，晋江市晋兴职业中专学校讲师，大学本科学历，研究方向：中职数学教学。

G718.3

A

1673-4564（2022）06-0169-04

2022—07—15