基于混合反向学习策略的鲸鱼优化算法*
2022-03-22耿召里曹淑睿刘昶忻
耿召里,李 目,曹淑睿,刘昶忻
(湖南科技大学信息与电气工程学院,湖南 湘潭 411201)
1 引言
优化问题一直是管理决策、计算机科学等领域研究的热点之一[1]。随着人工智能的兴起,对优化算法的研究与应用更显得尤为重要。智能优化算法是一类受自然界生物的社会行为启发而产生的算法,因其易于实现、结构简单、效果明显而受到广泛关注。最具代表性的有蚁群优化ACO(Ant Colony Optimization)算法[2]、粒子群优化PSO(Particle Swarm Optimization )算法[3]、人工蜂群ABC(Artificial Bee Colony)算法[4]、果蝇优化算法FOA(Fruit fly Optimization Algorithm)[5]等。2016年Mirjalili等[6]提出一种新型群体优化算法-鲸鱼优化算法WOA(Whale Optimization Algorithm)。WOA模拟了自然界座头鲸群体捕食猎物的行为,并将其抽象为搜索、攻击和包围3种行为对目标问题进行寻优。WOA相较于粒子群优化(PSO)算法[3]、萤火虫算法FA(Firefly Algorithm)[7]等具有原理简单、易于实现、参数少和寻优能力强等优点,目前已成功应用于滚动轴承故障诊断[8]、神经网络训练[9]和大规模优化问题[10]等领域。然而,由于标准的WOA近年来刚被提出,在很多方面还存在不足,如调整算法参数后仍不能完全模拟鲸鱼搜索过程[1],迭代后期群体多样性较差而导致算法陷入局部最优[11],解决高维复杂问题效果较差[10]等问题。针对这些问题,近年来国内外学者提出了多种WOA改进算法,有效地提高了算法效率。
为了解决鲸鱼算法易陷入局部最优和收敛精度低等问题,郭振洲等[12]提出了一种基于权重和柯西变异策略的鲸鱼算法,通过柯西变异,更新鲸鱼位置,有效地避免了算法陷入局部最优。褚鼎立等[13]通过研究个体与平均适应度之间的关系,提出了一种自适应权重策略的WOA算法,有效地提高了算法的收敛速度。王坚浩等[1]针对WOA开发和探索能力难以协调问题,设计了收敛因子和惯性权重的非线性混沌扰动协同更新策略,以平衡全局探索和局部开发能力。文献[14]针对鲸鱼优化算法全局收敛速度慢、优化性能有待提高等问题,将混沌理论引入WOA优化过程,用于调整迭代过程中鲸鱼优化算法的主要参数。然而,目前研究的鲸鱼优化算法求解高维复杂问题文献并不多,文献[15]提出一种基于Levey飞行轨迹的工程化WOA,提高了种群的多样性,增强了算法跳出局部最优的能力。文献[16]提出基于2个二进制变体的WOA,并应用于特征分类,取得了理想的效果。龙文等[10]采用对立学习策略初始化种群,并采用一种随机迭代参数非线性变化的收敛因子公式,展现了较强的计算能力。文献[17]提出了一种混合策略的鲸鱼优化算法MS-WOA(Mixed Strategy based improved Whale Optimization Algorithm),该算法引入非线性调整因子和自适应权重系数对鲸鱼位置进行更新,从而提高算法精度。
本文针对算法在求解高维复杂问题时存在收敛速度慢、全局开发能力不足等问题,首先引入一种自适应惯性权重,用于调节寻优前期的步长和寻优后期的种群多样性。其次,提出一种混合反向学习策略并嵌入到WOA中,用以提高算法收敛速度。最后引入一种参数非线性衰减策略,对WOA的收敛因子进行非线性调优,以便平衡算法全局和局部搜索能力。通过对10个函数的优化仿真,结果表明本文提出的基于混合反向学习策略的鲸鱼优化算法MWOA(Mixed inverse learning based Whale Optimization Algorithm)在解决高维复杂优化问题时的收敛速度和全局探索能力提升效果显著。在4个优化问题上与CPSO、CODE、EGWO和DIHS算法进行比较,结果表明MWOA具有较优的收敛精度。
2 鲸鱼算法
座头鲸是一种体型巨大的须鲸类鲸鱼,不同于其他齿类鲸鱼,座头鲸由于没有牙齿,只能靠捕捉体型较小的鱼虾为食,因而形成了一种特殊的捕食行为,即泡泡网觅食。Mirjalili等[6]将这种行为抽象为包围猎物、Bubble-net攻击和猎物搜索3个阶段,通过计算机仿真从而提出了鲸鱼算法(WOA)。
2.1 包围猎物
在座头鲸捕猎之初,目标个体在搜索空间中的位置不是先验已知的,但当前种群中最佳候选解与猎物之间的距离必定是最近的。因此,WOA假设当前搜索空间中最佳候选解为猎物的位置,或接近于猎物位置,则可根据当前最优解的位置更新其他个体的搜索位置,如式(1)和式(2)所示:
D=|C·Xbest(t)-X(t)|
(1)
X(t+1)=Xbest(t)-A·D
(2)
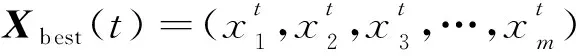
A=2αrand1-α
(3)
C=2rand2
(4)
其中,rand1和rand2元素值均为[0,1]的随机向量,α∈[α,α…,α],α是一个从2随t线性下降到0的收敛因子,如式(5)所示:
α=2-2t/T
(5)
其中,t为当前迭代次数,T为最大迭代次数。
2.2 Bubble-net攻击
鲸鱼是以螺旋式上升并不断收缩包围范围的方式捕获猎物的,WOA将这种行为描述为收缩包围策略和螺旋式上升策略。
(1)收缩包围策略:通过减小式(3)中的a值来实现,如式(3)所示,A的值域为[-a,a],当a随着迭代次数的增加从2降为0时,则搜索个体的新位置可以被定义在个体原始位置与当前最优位置的之间的任意值,达到包围猎物的目的。
(2)螺旋式上升策略:该方式首先计算搜索个体位置与最优解之间距离,而后在各个个体与最优个体之间建立一个螺旋公式,如式(6)所示,模拟鲸鱼螺旋上升的运动状态。
X(t+1)=
|Xbest(t)-X(t)|eblcos(2πl)+Xbest(t)
(6)
其中,b为常数,决定了对数螺旋的形状,l是[-1,1]的一个随机数。
鲸鱼的收缩包围行为和螺旋式上升行为是同步进行的,为了模拟这种同步行为,设鲸鱼进行收缩包围和螺旋上升的可能性均为0.5,则可用式(7)模拟这一行为。
(7)
其中,p为[0,1]的随机数,p≥0.5时执行螺旋上升策略,p<0.5时,执行收缩包围策略。
2.3 猎物搜索
鲸鱼执行搜索策略是基于可变向量A进行的,鲸鱼会根据彼此的位置进行随机搜索,当|A|>1时,表明鲸鱼在收缩攻击圈之外,WOA算法不再选择最优个体作为参考对自身进行更新,而是执行随机搜索,随机搜索以一个个体作为目标再进行位置更新。可用式(8)和式(9)表示这一行为。
D=|C·Xrand(t)-X(t)|
(8)
X(t+1)=Xrand(t)-AD
(9)
其中,Xrand(t)为随机选取的目标个体位置。
从上述可知,A对鲸鱼算法起着极其重要的作用,当|A|>1时,算法进行随机搜索,寻找更好的最优解,当|A|≤1时,种群不再进行随机搜索,而转向攻击策略,集中收缩攻击目标猎物,因此A影响着算法的全局搜索和局部开发能力,原始鲸鱼优化算法具体执行过程见文献[6]。
3 基于混合反向学习策略的鲸鱼优化算法(MWOA)
3.1 WOA存在问题与改进策略
在实验中,发现原始WOA算法在求解高维复杂问题时存在收敛速度慢、全局搜索能力不足等问题,主要表现为算法无法收敛到收敛域内、收敛精度不高,其原因在于在搜索后期,随着迭代次数的增加,|A|<1的机率变大,导致整个种群都向最优解靠近而陷入局部最优,导致多样性降低,全局搜索能力下降。
为了解决上述问题,MWOA在WOA的基础上作了如下改进:(1)引入一种新型自适应权重策略,以平衡寻优前期的个体步长和后期的种群多样性,提升寻优精度;(2)提出一种混合反向学习策略,以防止算法陷入局部最优,提高算法全局搜索能力;(3)针对算法后期收敛速度慢等问题,引入非线性收敛因子改进策略,加快算法的收敛速度。
3.2 惯性权重自适应
惯性权重对鲸鱼优化算法的收敛速度和寻优精度起着至关重要的作用,合适的惯性权重对算法寻优探索能力具有极大帮助,本文受文献[18]的启发,引入一种自适应策略的惯性权重,如式(10)所示。
w=d1*(Xbest(t)-X(-1)(t))+
d2*(ub-lb)/t
(10)
其中,Xbest(t),X(-1)(t)为当前种群的最优最差个体位置向量,ub与lb分别为种群的位置的上界和下界。t为种群当前迭代次数。d1和d2为2个常数,均取0.000 1。该策略惯性权重被分为前后2个部分,后半部分在算法前期遇到陷入局部最优的时候可以起到主导作用,从而使其跳出局部最优。随着当前迭代次数t的增大,后半部分对权重ω的影响逐步减弱。因此,在迭代后期若最优个体与最差个体之间差异较大,则前半部分对权重ω起着主导性作用,从而加大步长,提升种群多样性。
3.3 混合反向学习策略
反向学习是2005年由Rahnamayan等[19]提出的,作者认为,从当前种群中随机生成解决方案往往会导致方案中没有较理想的区域,而反向学习策略既考虑了候选解决方案又考虑到了与之相反的解决方案。因此,已有许多研究人员将这种学习机制引入到算法应用中,如王振东等[20]应用反向学习策略初始化天牛算法初始种群,肖子雅等[21]将精英反向学习策略融入到黄金正弦鲸鱼优化算法中,加快了算法的收敛速度。本文提出一种混合反向学习策略,并将其与WOA相结合。
混合反向学习策略同时考虑了优化后期最优解与最差解的状态,针对最优解而言,为了防止算法陷入局部最优,而减弱全局探索能力,对其进行一般反向学习操作,以提高其局部探索能力,如式(11)所示:
Xbest(t+1)=lb+(ub-Xbest(t))
(11)
其中,ub与lb分别为鲸鱼位置向量的上界和下界,Xbest(t)为最优个体位置向量。
针对最差位置的个体,为了保证算法的全局搜索能力,这里对其进行随机反向学习操作,如式(12)所示:
X(-1)(t+1)=lb+rand·(ub-X(-1)(t))
(12)
其中X(-1)(t)为最差的个体向量,rand为与ub同维度的随机向量。
混合反向学习与精英反向学习的区别有如下几点:(1)混合反向学习与精英反向学习的对象不完全等同,精英反向学习的对象是群体中最优的前m个个体,而本文中混合反向学习的对象为最优个体和最差个体。(2)本文中的参数是选取种群位置的上界和下界,而精英反向学习的ub与lb值为前m个个体的上界和下界。
3.4 非线性收敛因子改进策略
由文献[6]可知,鲸鱼优化算法的探索开发能力主要取决于收敛因子α,当α较大时,算法具有较强的全局搜索能力,当α较小时,算法局部搜索能力增强,因此,为了平衡算法的全局搜索与局部搜索之间的关系,本文引入文献[10]中提出的收敛因子非线性改进方法,如式(13)所示:
(13)
其中,αinitial和αfinal为α的起始值和终止值,t为当前迭代次数,T为最大迭代次数,μ为线性权重因子,此处μ取25[10]。
3.5 MWOA算法步骤
算法1给出了MWOA的执行伪代码,图1为MWOA的执行框图。
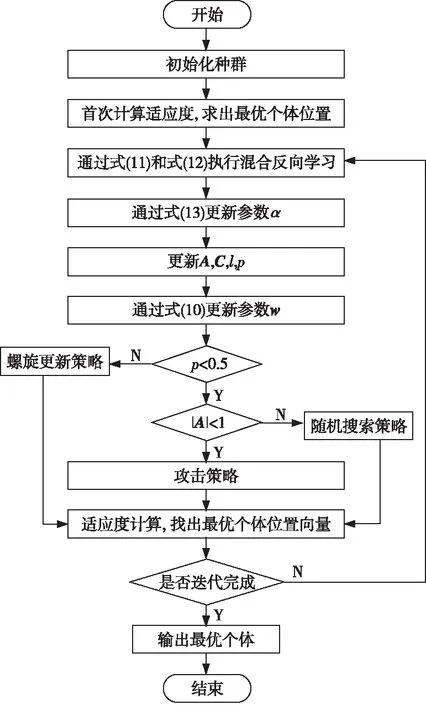
Figure 1 Flowchart of the MWOA algorithm图1 MWOA 算法流程图
算法1MWOA算法
Input:population sizeN,maximum iterationT,dimensionD,data upper limitub,data lower limitlb.
Output:best solution vectorX*.
1.Initialize the whales populationsXi(i=1,2,…,N);
2.Calculate the fitness of each whale,X*←the best search whale;
3.While(t 4. UpdateX*by Eq(11) and Eq(12); 5. Execute mixed reserve learning strategy by Eq(11) and Eq(12); 6.Foreach search whale 7. UpdateA,C,landp; 8. Updateαby Eq(13); 9. Updatewby Eq(10); 10.If(p<0.5) 11.If(|A|≤1) 12. Update the position of the search whale by Eq (2); 13.Elseif(|A|>1) 14. Update the position of the search whale by Eq (9); 15.Endif 16.Elseif(p≥0.5) 17. Update the position of the search whale by Eq (6); 18.Endif 19.Endfor 20. Calculate the fitness of each while; 21. Update the betterX*; 22.Endwhile 23.ReturnX*. 为了验证MWOA算法的性能,本文选取文献[10]中的f1、f2、f3、f5和文献[1]中的f5~f10作为本次数值测试的F1~F10。针对本文的研究目标,选取了3个评价指标对算法进行评价: 第1个为精度AC(Accuracy),如式(14)所示,用以评价所求解与全局最优解之间的差距。 AC=|F(Pbest)-F(Xopt)| (14) 其中,Pbest为寻优迭代后的所求解,Xopt为全局最优解,F()为优化问题的抽象函数模型。 第2个评价指标为标准差(STD),如式(15)所示,标准差主要是用于评价算法的鲁棒性能,衡量算法的稳定性。 (15) 其中,Z为总的实验次数,xi为第i次的实验结果,υ为Z次实验结果的平均值,STD为Z次实验结果的标准差。 第3个评价指标为搜索成功率SR(Success Rate),如式(16)所示: (16) 其中,Z为实验的总次数,Z′为搜索成功收敛到指定收敛精度内的次数。 采用MWOA算法对上述10个函数进行求解,函数的维度分别设置为200维,500维和1 000维,并与WOA、MS-WOA[17]和IWOA[10]进行比较。针对上述算法,均采用最大迭代次数T=500,种群规模N=30。为了排除算法偶然性,对上述算法均独立运行30次后选取平均精度、成功率和平均精度标准差对算法性能进行分析,迭代结果如表1所示,表中加粗部分表示该算法在对应函数和维度上得到的性能指标的最优值。 Table 1 Comparison of optimization performance of four algorithms on different functions and dimensions 从表1中可以看出,除了维度为500时,在函数F6和F8上MS-WOA的平均寻优精度略高于MWOA和其他算法的,在其他维度上,MWOA不论是寻优精度还是寻优成功率均优于其他算法。在函数F4和F10上,MWOA的寻优精度远高于其他算法的,寻优成功率则略优于对比算法。在函数F2和F8上,尽管各算法的寻优成功率均为100%,但是,MWOA的寻优精度明显高于其他算法的。而在F1、F5、F7和F9上,各个算法的寻优精度和成功率均相同。为了观察算法在各个函数上的寻优迭代情况,图2给出了维度为500时各算法在10个函数上的迭代情况。从图2中可以看出,在函数F1、F5、F7和F9上,尽管各函数均能够收敛到全局最优,MWOA的收敛速度却明显快于其他算法的。 Figure 2 Iterative of four algorithms on each function when dimension is 500图2 维度为500时4种算法在各函数上的迭代情况 本文针对WOA引入了3种策略,即(1) 自适应惯性权重;(2)混合反向学习策略;(3)非线性收敛因子改进策略。为了研究3种策略对WOA迭代效果的影响,对选取的10个优化函数进行优化求解。将MWOA与只采用自适应惯性权重的WOA(记作WOA-1)、只采用混合反向学习策略的WOA(记作WOA-2)和只采用非线性收敛因子的WOA(WOA-3)进行比较,4种算法的参数设置同4.2节,表2所示为4种算法在函数维度为500时的寻优性能比较。 从表2可知,3种改进策略对算法的精度均有提高作用,但WOA-2对精度的提升作用略差,WOA-1和WOA-3二者对精度提升的作用不相上下。 Table 2 Comparison of performance of four algorithms when dimension is 500 为了进一步论证算法的有效性和可行性,用本文算法对文献[10]中的f2、f5、f9、f124个复合函数进行求解,并与混沌粒子群优化CPSO(Chaos Particle Swarm Optimization)算法[22]、组合差分进化CODE(COmbined Differential Evolution)算法[23]、改进灰狼优化EGWO(Extended Grey Wolf Optimizer)算法[24]、动态调整维数的和声搜索DIHS(Dynamic-dimensionality-reduction-adjustment and dynamic fret width strategy based Improved Harmony Search)算法[25]4种算法进行比较,为了保证公平性,3种算法种群大小均设置为30,迭代次数为500次。CPSO算法其他参数相关参数参照文献[22]设置,CODE其他参数设置同文献[23],EGWO算法其他参数参照文献[24]设置,DIHS算法的其他参数参照文献[25]进行设置,实验结果如表3所示。从表3中可以看出,针对函数f9,CODE、CPSO、EGWO、DIHS和MWOA均有比较好的效果,但MWOA效果明显优于其他对比算法的;在f2和f52个函数上,相较于CODE、CPSO、EGWO和DIHS,MWOA的求解精度略高。在函数f12上,DIHS获得了最优的求解精度,MWOA的精度则略低于DIHS的,高于CPSO、CODE和EGWO的。因此,从总体上看,相较于其他几类优化算法,MWOA仍然具有明显的优势,具有较好的收敛精度和精度均方误差。 Table 3 Comparison of optimization effects of five algorithms 鲸鱼优化算法WOA是近年提出的一种启发式算法。针对鲸鱼优化算法在求解高维复杂问题时存在的不足,本文提出一种基于混合反向学习策略的鲸鱼优化算法MWOA,得出以下结论: (1)针对收敛精度问题,选取10个基准函数进行实验,分别在维度为200,500,1 000时进行实验,结果表明,相较于MS-WOA与IWOA,MWOA具有较高的收敛精度和寻优成功率。 (2)针对收敛速度问题,在选取的10个优化函数上进行仿真,结果表明,MWOA的收敛速度要优于WOA、IWOA和MS-WOA的。 (3)为了验证MWOA有效性,在4个基准函数上,分别与CODE、CPSO、EGWO和DIHS算法进行比较,得出本文提出的MWOA具有较好的收敛精度。 (4)MWOA算法在求解较复杂高维函数时具有较好的效果,但是,对于求解特别复杂的复合函数,结果仍然不理想。下一步的工作重点是研究如何提高MWOA求解特别复杂的复合函数的精度。4 数值实验及比较
4.1 基准测试函数和评价指标
4.2 在基准函数上的算法性能分析
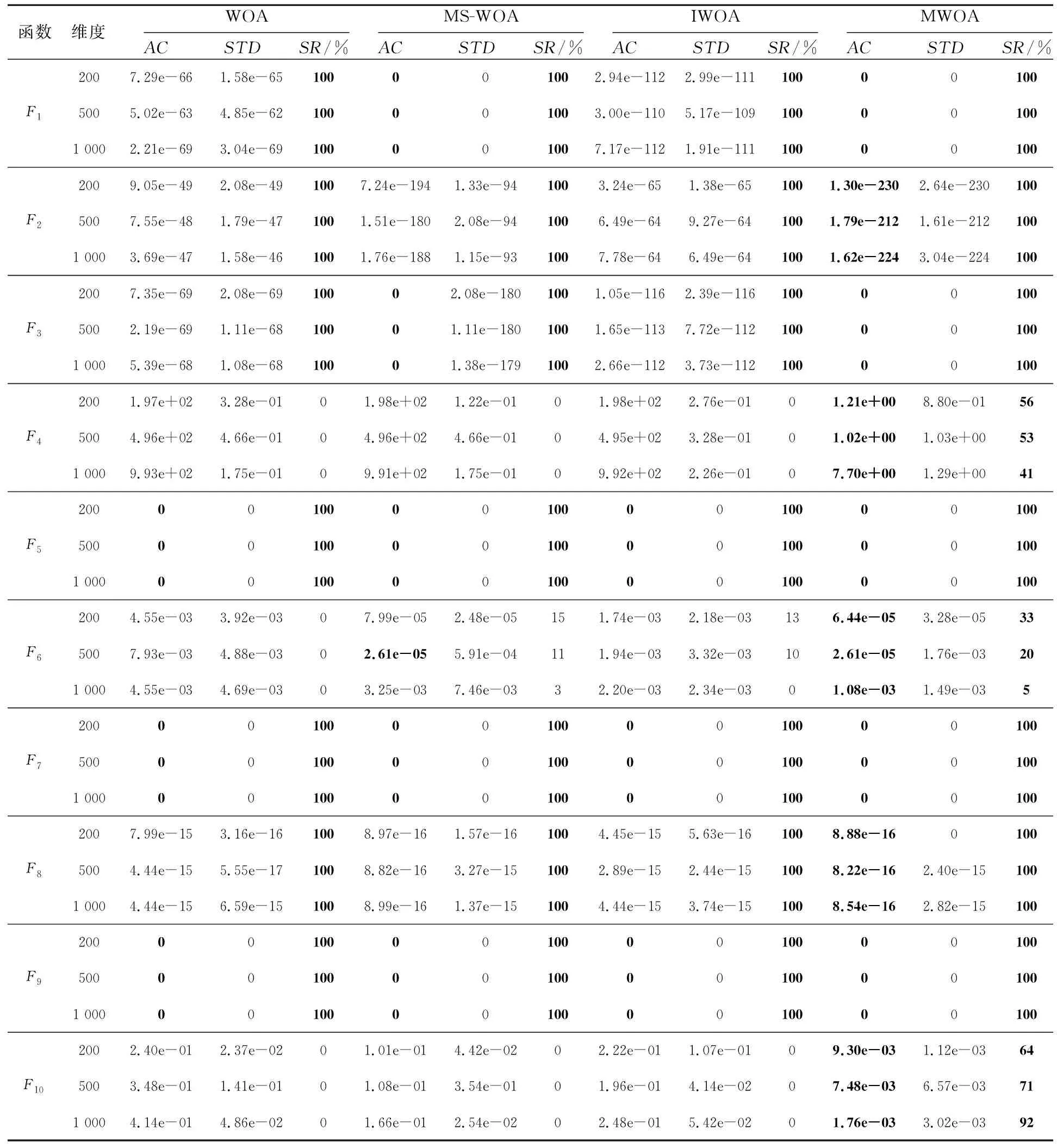
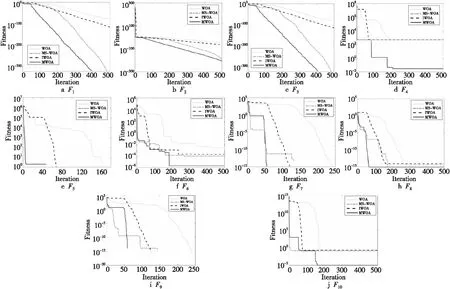
4.3 3种改进策略的改善性能分析
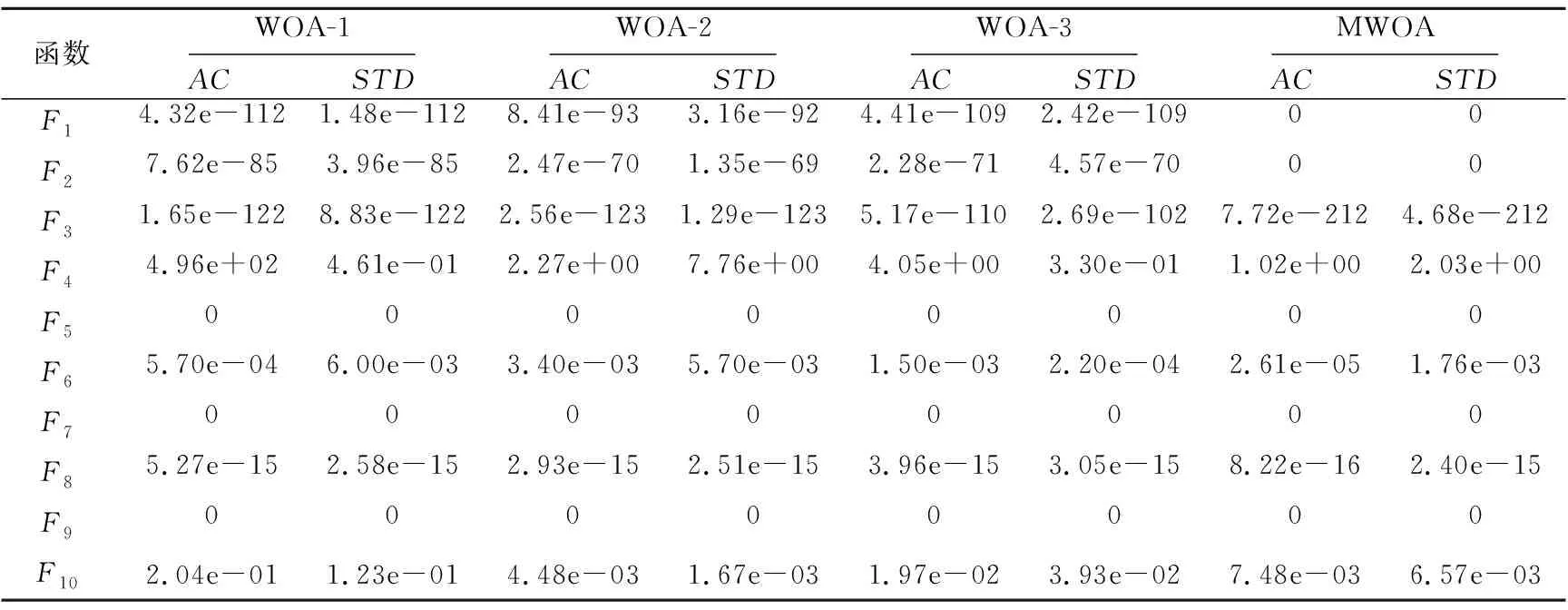
4.4 与其他优化算法的比较分析
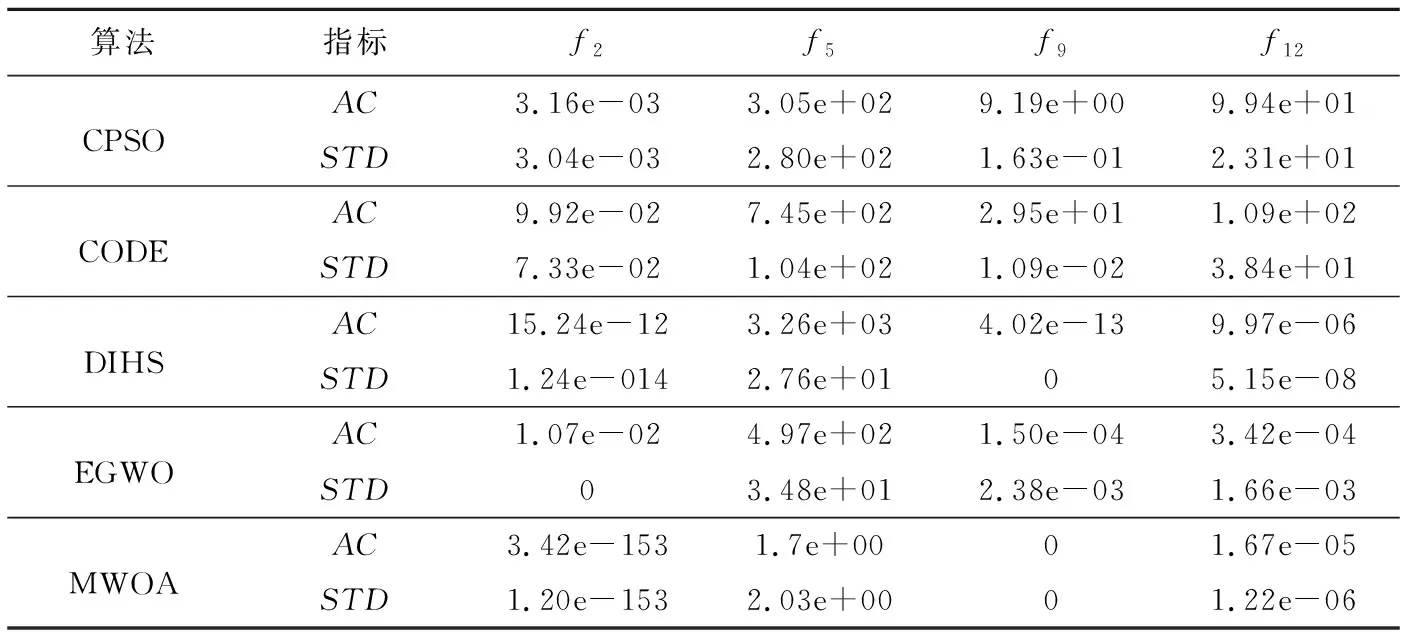
5 结束语
