建系有法可依 立几有章可循——向量建系法在立体几何问题中的应用

顾予恒, 卢成娴

(杭州第二中学钱江学校，浙江 杭州 311215)

立体几何是高中数学的重要组成部分，主要考查学生的直观想象和逻辑推理的素养．空间向量法的引入，将几何问题转化为代数问题，可以借助向量的运算，程序化地“算出”几何的结果，减少了复杂的思维和推理过程，为空间感较弱的学生提供了“救命稻草”，因此备受师生们的青睐，建系已经成为解决立体几何问题的一种常用方法[1]．

但在日常教学中，很多教师往往更多关注于各种求证与求值公式的运用，而忽略了问题的第一步：建系、设点．事实上，在很多试卷中出现了不易建系的题目，让学生措手不及．学生把各解题公式背得滚瓜烂熟，哪知第一步建系都建不对．答案中的第一步“如图，建系设点……”真的是显然吗？可以说，建系设点是向量法解决立体几何问题中蕴涵几何味的关键所在，也是学生运用向量法的难点．

与平面坐标系相比，空间坐标系将二维平面推广到三维空间，二者最大的差别是z轴，因此，z轴是关键．纵观2021年各省市地区高考试题中的立体几何问题，图形虽然纷繁多样，但从空间向量法的角度来看，最主要的差别是如何建系．本文以2021年的数学高考真题为例，从“建z轴”的角度整理了几种不同类型的建系方法，供大家参考．

1 常见立体几何建系类型

类型1线面垂直“定”z轴.

这一类型最简单，其特点是题干给出“线面垂直”这一条件．在建系时，一般选择垂直于底面的这条线(或这条线的平行线)作为z轴，然后建立合适的x,y轴．

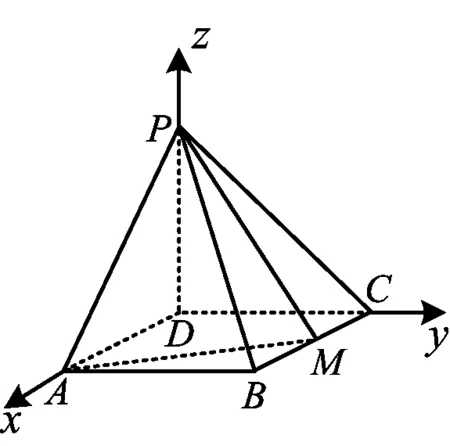
图1

例1如图1，四棱锥P-ABCD的底面是矩形，PD⊥底面ABCD，PD=DC=1，M是BC的中点，且PB⊥AM．

1)求BC；

2)求二面角A-PM-B的正弦值．

(2021年全国数学高考乙卷理科试题第18题)

分析由于本题题干中出现了“PD⊥面ABCD”这一条件，因此可以直接选择PD作为z轴．又因为底面是矩形，所以可以选择以点D为原点、以DA,DC,DP为x,y,z轴建系．

类型2面面垂直“作”z轴.

这一类型的特点是题干给出“面面垂直”这一条件．在建系时，一般根据面面垂直的性质，在垂直于底面的侧面上作一条直线垂直两面的交线，则所作的直线与底面垂直，即这条直线可以作为z轴．

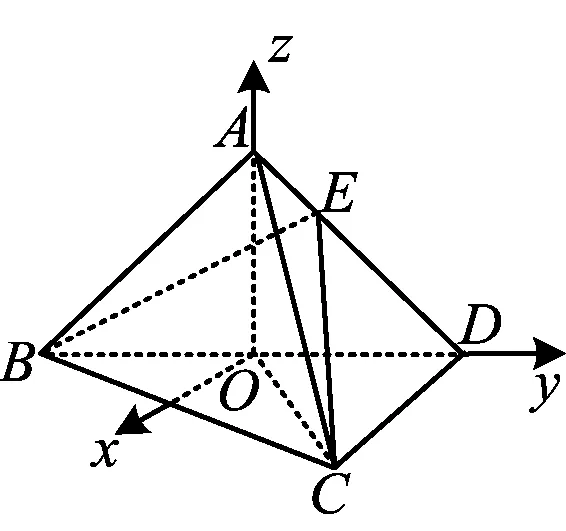
图2

例2如图2，在三棱锥A-BCD中，平面ABD⊥平面BCD，AB=AD，O为BD的中点．

1)证明：OA⊥CD；

2)若△OCD是边长为1的等边三角形，点E在棱AD上，DE=2EA，且二面角E-BC-D的大小为45°，求三棱锥A-BCD的体积．

(2021年全国数学高考卷Ⅰ试题第20题)

分析由题干可知AB=AD，又O为BD的中点，从而AO⊥BD．因为面ABD⊥面BCD，面ABD∩面BCD=BD，所以AO⊥面BCD．因此，AO即为要作的z轴．另外根据第2)小题知，需在底面BCD内另作一条与OD垂直的直线作为x轴．因此，以O为原点建系(如图2)．

类型3底面垂直“造”z轴.

这一类型的特点是根据题干所给条件，找不到面或线垂直底面．在建系时，一般选择底面上互相垂直的两条直线作为x，y轴，另外“造”一条底面的垂线作为z轴．

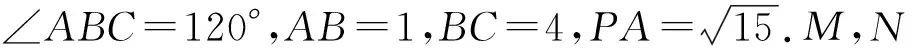
1)证明：AB⊥PM；

2)求直线AN与平面PDM所成角的正弦值．

(2021年浙江省数学高考试题第19题)

方法1由题干条件可知底面ABCD是平行四边形，∠BCD=60°，CD=AB=1，CM=2，从而CD⊥DM．

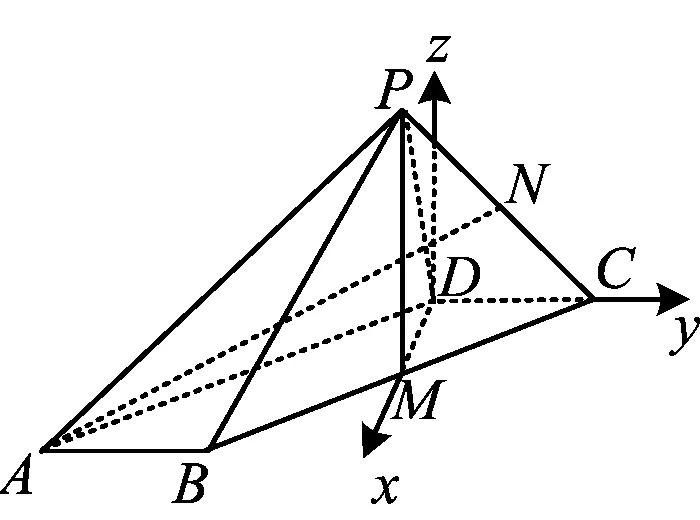
图3

因为没有现成的直线与底面ABCD垂直,所以以点D为原点、以DM,DC为x,y轴，过点D作z轴垂直底面ABCD建系(如图3)．

由于z轴是单独“造”出来的，因此几何体中部分点的坐标不能直接“读”出．如点P，我们可以先设坐标，再通过运算“求”出．

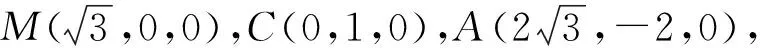
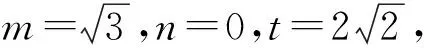
由此可见，对于坐标不易直接“读”出的点，我们可以先设其坐标．坐标中的这n个未知数，可以通过寻找与该点相关的n个条件，对应建立n个方程，从而算出点的坐标．

事实上，除了直接“造”z轴外，若对几何体进一步分析可知PM⊥面ABCD．第1)小题在善意地提醒考生有线面垂直，可将此题转化为类型1：线面垂直定PM为z轴．因此，有时题干中不直接出现垂直，但要证明的结论里隐藏着垂直，对解题有很好的启示作用．

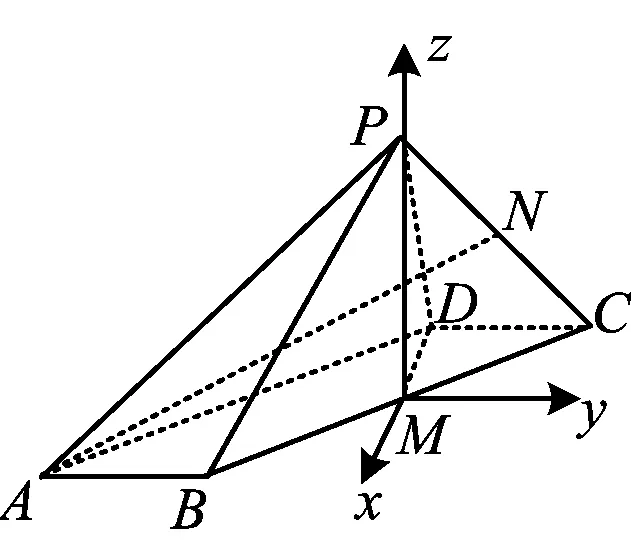
图4

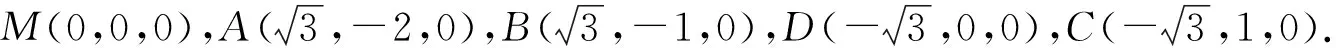
对比上述两种方法可知：方法1重在程序化的运算；若能数形结合，通过几何分析找到垂直和数量关系，则采用方法2可以大幅降低运算量．这恰恰是本题的魅力所在，不偏不倚，无论建系法还是几何法都没有太占便宜．想得多一点就可以算得少一点，想得少一点就要算得多一点．

线面垂直定z轴、面面垂直作z轴、底面垂直造z轴，这3种建系类型为解决立体几何问题提供了有效法则．下面以近5年浙江省高考立体几何大题为例，梳理以上3种建系法的应用，如表1所示．

表1 2016—2020年高考浙江卷中3种建系方法的应用情况

由表1可知，3种建系方法在前5年浙江省高考立体几何解答题中均有所应用，其中应用较多的还是“面面垂直作z轴”．由此可见，利用面面垂直的性质定理作垂线是浙江省数学高考的一个热点问题．

2 向量建系法在翻折问题中的应用

立体几何问题首先要依托于几何体，几何体的构建方式主要有两种：切割与翻折．上述的讨论均是在切割体(主要是从长方体中切割而来的多面体)中的应用．那么，对于翻折问题，这3种建系方法是否依然适用呢？答案是肯定的！

下面通过一道例题简单介绍空间向量法在翻折问题中的应用．

例4已知等边△ABC的边长为4，M,N为AB,AC的中点，如图5，沿MN将△AMN折起.当直线AB与平面BCNM所成的角最大时，线段AB的长度为

( )

分析翻折是一个动态变化的过程，本题中点A是图形真正变化的元素．由于没有现成的垂直，因此在建系时，采用类型3，需要另外单独“造”z轴．在设点时，可以选取翻折角度(设为θ)为变量．

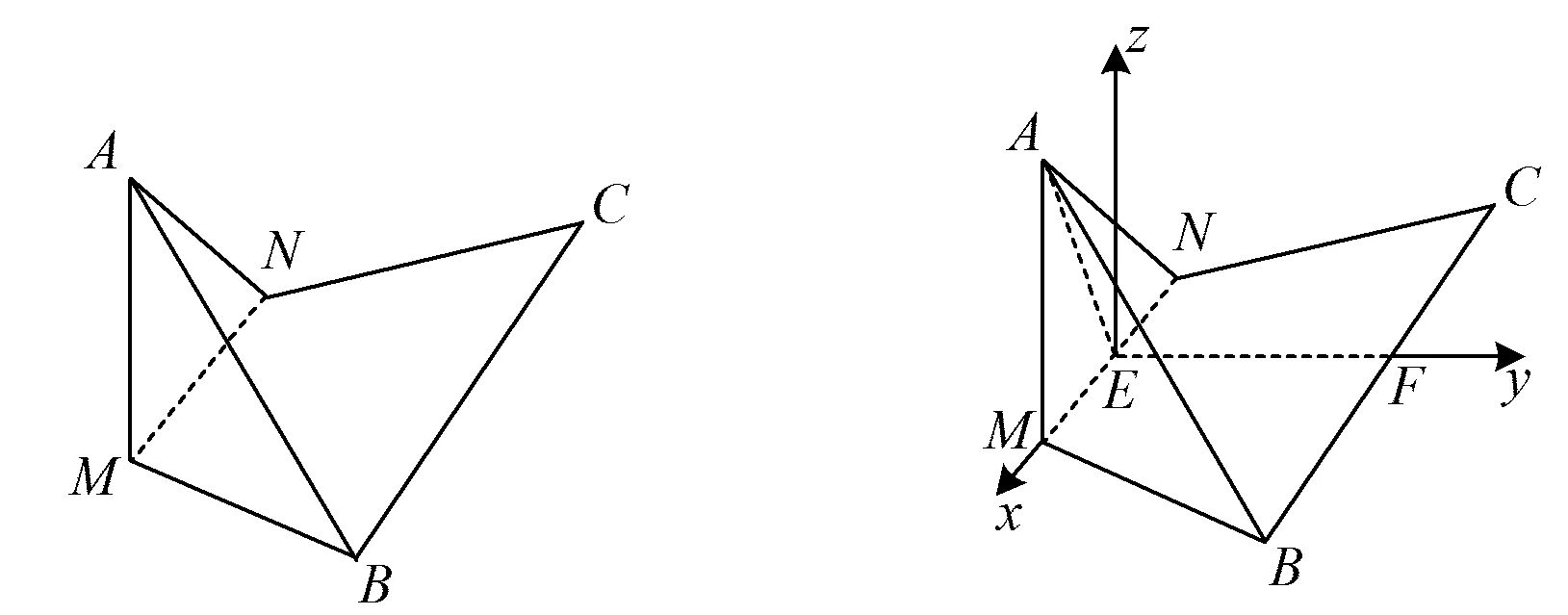
图5 图6

解因为等边△ABC是对称图形，所以取MN和BC的中点E,F，联结EF，则MN⊥EF．以E为坐标原点、分别以EM,EF所在直线为x,y轴，过点E作z轴⊥底面MBCN建系(如图6)．

设直线AB与平面BCNM所成的角为α，则

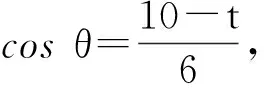
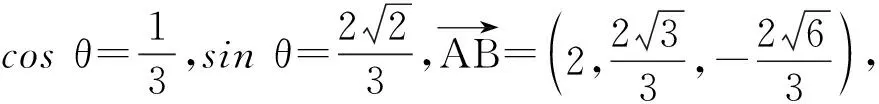
例4是将等边三角形沿着中位线进行翻折，如果改为正方形沿着对角线翻折，就变成了2021年1月的浙江学考题．

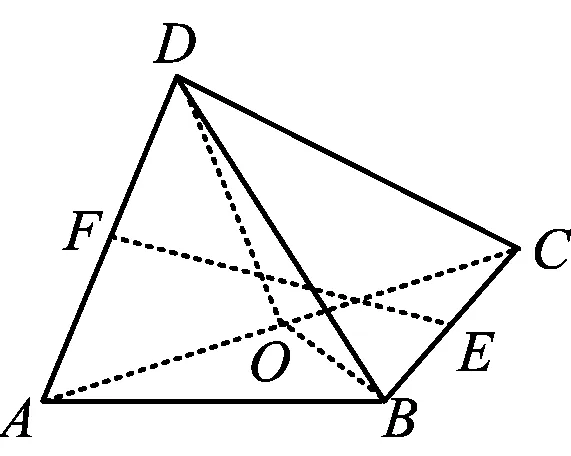
图7

变式1如图7，在三棱锥D-ABC中，AB=BC=CD=DA，∠ABC=90°,E,F,O分别是棱BC，DA，AC的中点.记直线EF与平面BOD所成角为θ，则θ的取值范围是

( )

(2021年1月浙江省数学学考试题第18题)

分析虽然题干条件中并未出现“翻折”二字，但事实上，此题中点D的位置是不确定的．若以动态视角来看，这个几何体可以看做是一个正方形沿着对角线AC翻折得到．随着翻折角度的变化，θ也跟着变化．由此可见，这是一道经过“包装”的翻折问题．

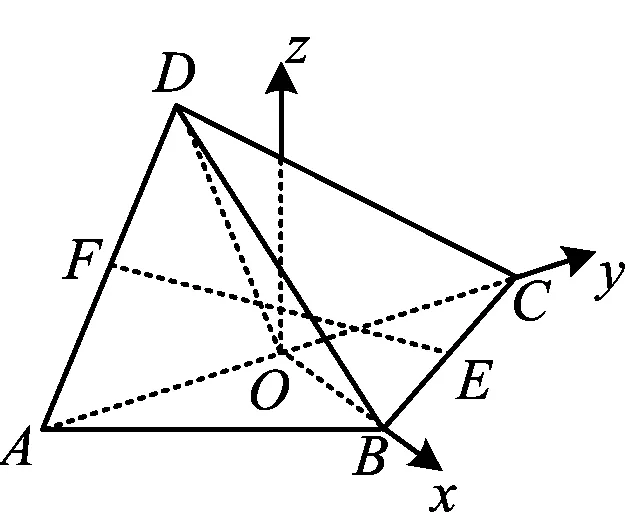
图8

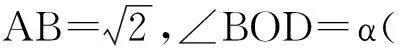
A(0,-1,0),D(cosα,0,sinα),

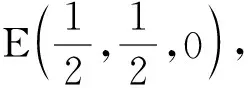
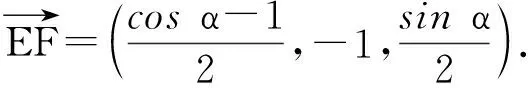
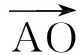
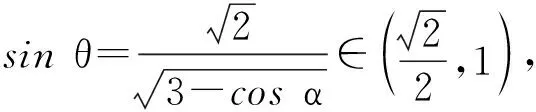
3 向量建系法在几何命题中的应用

由此，我们发现用建系法解决翻折问题，一般都可以通过“造”z轴建立坐标系，以翻折因素(如角度、长度)为变量设点，实质就是通过运算求出动点的坐标．抓住了这个核心方法，我们还可以利用建系法来构造几何体[2]．

例如，我们对变式1进一步改编，可构造新的几何体．为了让几何体更加新颖，可以将变式1中的底面Rt△ABC改为直角梯形ABCD．设△PAD为等腰直角三角形，AP⊥PD，CD⊥AD，AD=2DC=2BC=2(如图9)．为了加大难度，可以选择△PAD沿着AD翻折60°时的情况，一旦翻折到位，这个几何体就是一个确定的几何体，此时可以通过建系法确定点P的位置．我们还可以通过“包装”，隐去“翻折60°”的条件．通过计算可知当翻折60°时，棱长PC恰好为2，故可以用PC=2作为条件来代替．这样，一道立体几何题的几何体就构造完成了．

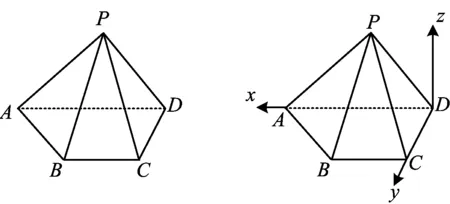
图9 图10

变式2如图9，在四棱锥P-ABCD中，△PAD是以AD为斜边的等腰直角三角形，BC∥AD，CD⊥AD，PC=AD=2DC=2BC=2．

命题角度1建系设点定图形.

命题1请建立合适的空间直角坐标系，并写出各点坐标.

分析由题干可知，此题需要单独“造”z轴．注意到底面ABCD中有CD⊥AD，因此可取点D为原点、以DA，DC为x，y轴，再确定z轴建系．

解得

故

为了使几何体元素更加丰富，我们可以增加点和直线，如取PD的中点E，联结CE．基于这一图形，我们可以从证明平行垂直、求空间角、计算距离等角度编制问题．

命题角度2平行垂直“算”证明.

命题2证明：CE∥平面PAB．

命题角度3公式得出线线角.

命题3求异面直线AB与PD所成角的余弦值.

命题角度4公式求解线面角.

命题4求直线CE与平面PBC所成角的正弦值.

命题角度5公式计算二面角.

命题5求二面角P-AD-B.

命题6求二面角A-PB-C的余弦值.

命题角度6各有妙招求距离.

命题7求点E到直线AB的距离.

命题8求点E到平面PBC的距离.

命题9求直线CE与平面PAB间的距离.

命题10定义：两条异面直线之间的距离是指其中一条直线上任意一点到另一条直线距离的最小值．请用这一定义，求直线AB与PD之间的距离．

命题角度7空间向量的问题.

事实上，这些命题与条件“PC=2”是等价的，只要将其中任何一个命题作为条件，这个四棱锥就唯一确定，也就可以推导出其他10个命题．2017年浙江省数学高考立体几何解答题就是以本题题干为背景，上述命题2与命题4即为高考原题．

4 结束语

由上述分析可知，无论是切割模型还是翻折模型，空间向量法可以说是一种“万能”的解法．它的本质是方程思想，通过坐标的代数运算解决几何问题．日常教学中要引导学生关注本质，不仅要会算，更要知其然而知其所以然[3]．本文总结的3种类型就是让建系设点“有法可依”，让立体几何难题“有章可循”，能有效弥补部分学生空间想象能力的不足，对广大学生来说是个“福音”．