地铁盾构区间近距离下穿顶管隧道力学响应及沉降控制标准研究

杨艳玲，韩现民，李文江

(1.中铁隧道集团二处有限公司，河北三河 065201；2.石家庄铁道大学，石家庄 050043；3.河北省金属矿山安全高效开采技术创新中心，石家庄 050043)

引言

随着城市轨道交通的不断发展，新建隧道近接下穿既有地下结构施工控制已逐渐成为地铁建设过程中日益突出的热点工程问题之一。研究揭示地铁隧道下穿施工引起的既有结构变形规律，科学制定下穿施工过程位移控制标准，对合理制定施工方案、实现下穿施工安全管理具有重要意义。目前，在既有结构变形规律预测和沉降控制标准方面，部分成果是建立在经验公式(如Peck沉降曲线公式或区域性相关工程测试数据回归公式)基础之上的，比如郭亮[1]通过Peck公式得到了地表最大沉降量和地铁轨道倾斜率的关系，从而得到了满足行车安全下的地表最大允许沉降；朱衍峰[2]通过Peck公式建立了地表最大沉降量和建筑物倾斜率的关系，从而得到了满足建筑物结构安全条件下的地表允许沉降。其他学者研究成果亦和前者类似[3-5]，其相应成果的针对性、可靠性、精准性均有待发展和提高。虽然也有建立在数值仿真技术基础之上的研究成果，如毛新颖等[6]通过数值模拟研究了盾构施工对地表沉降槽变化的影响；赵强政[7]通过数值模拟研究了盾构隧道施工对地层隆沉、道路倾斜率等的影响；黄世政[8]通过数值模拟研究了盾构下穿既有隧道过程中，既有隧道的变形规律及受力规律。但其研究过程中工作量大且其成果方法的系统性、完整性仍有待完善。目前，在盾构穿越建(构)筑物施工扰动影响研究方面，常见的研究对象有地铁隧道[9-15]、地铁车站[16]、地下管线[17]、桩基[18]和地表建筑物[19-20]，而大断面顶管隧道受管节接头特性影响，对下穿施工扰动具有高敏感性和低适应性，相对于其他既有地下结构，其沉降控制要求更为严格，但相关研究成果较少。

以郑州地铁4号线会展中心站—商鼎路站区间盾构隧道近距离斜穿既有交通顶管隧道群区段为工程背景，开展下穿既有顶管隧道施工力学响应及沉降控制标准研究，提出下穿施工过程既有顶管隧道沉降控制标准的制定方法，制定相应的控制标准和管理基准，为依托工程提供技术支持，为类似工程提供借鉴经验。

1 依托工程概况

郑州市轨道交通4号线会展中心站—商鼎路站区间为盾构区间，右线DK20+750.655～DK20+799.989、左线DK20+741.626～DK20+825.483区段以平面交角37°近距离下穿福元路—商鼎路交通顶管隧道群，新建隧道埋深17.5 m，隧道结构拱顶距顶管隧道底部边缘最小间距为2.94 m，下穿段平面位置关系如图1所示。

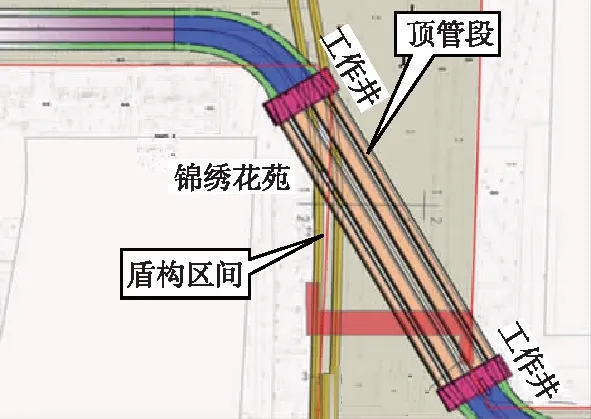
图1 既有顶管隧道与盾构区间位置关系

盾构区间管片内径为550 cm，外径为620 cm，厚度为35 cm，两隧道中心线间距为16 m。福元路—商鼎路隧道为市政道路矩形顶管隧道，由4条顶管隧道构成，包括2条非机动车顶管隧道和2条机动车行车顶管隧道。机动车道隧道管节尺寸为：1.5 m(长)×10.4 m(宽)×7.5 m(高)，壁厚700 mm。非机动车道隧道管节尺寸为：1.5 m(长)×6.9 m(宽)×4.2 m(高)，壁厚450 mm。顶管隧道管节均采用承插式接头，接头形式如图2所示。

图2 既有顶管接头形式

盾构区间下穿福元路—商鼎路隧道处地层种类较多，有杂填土、黏质粉土、粉质黏土、粉砂和细砂，区间所穿越地层为粉质黏土、粉砂层。经勘察，在46 m深度范围内共观测到2层地下水，分别为：潜水，其稳定水位埋深9.2～11.7 m；微承压水，稳定水位埋深14.1～16.7 m，承压水头为4.0～6.5 m。

2 下穿施工数值模拟

2.1 计算模型

为预测下穿施工过程中既有结构的变形规律和量值，寻找和发现施工变形的关键控制工况，并为下穿施工过程既有顶管隧道变形控制标准的制定提供理论基础，研究中采用有限差分程序建立三维地质力学模型，对下穿施工过程进行了数值模拟。根据工程实际情况，模型尺寸：长度取140 m，宽度取99 m，高度为55.5 m。计算模型中隧道结构、注浆体、土体均采用实体单元模拟，盾构机头采用壳单元模拟。单元数量为194 120个。具体模型如图3所示。除地表设置为自由面外，其他各面均采用法向位移约束边界。地层采用摩尔库伦本构模型，隧道管片采用弹性本构模型。盾构掘进过程参阅文献[21]进行模拟计算，关键点为单元“生死”、土舱压力与注浆压力模拟。

图3 数值计算模型

模拟中，在既有顶管底板不同位置共设置7个监测点(如图4(a)中M1～M7)及8条测线(如图4(b)中Ⅰ～Ⅷ)，以便于监测分析不同工况下既有隧道变形与受力特点，以及其演化规律，具体测点及测线的布设情况如图4所示。根据施工组织安排，本工程执行新建隧道右线先行的原则，即当右线隧道完成下穿段施工后再进行左线隧道掘进。

图4 计算模型中测点及测线布设示意

2.2 计算参数选取

数值分析中的地层和结构物理力学参数取值如表1、表2所示。

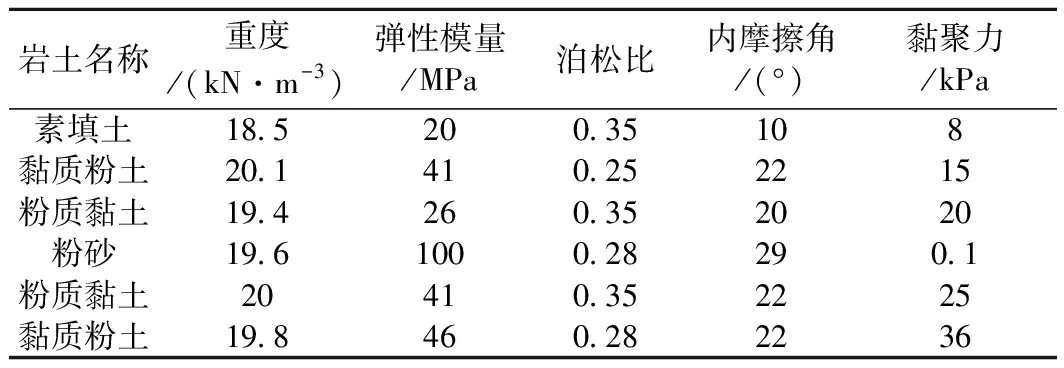
表1 地层物理力学参数

表2 结构参数

3 数值模拟结果

3.1 既有隧道底板测点沉降计算结果

掘进过程中既有顶管隧道底板测点沉降变形监测结果如图5所示。

图5 掘进过程中监测点竖向位移变化曲线

图5中施工步序的含义为：步序1是指新建右线隧道掌子面掘进至监测点M1下方，步序2为右线隧道掘进至监测点M2下方，步序3为右线隧道掘进至监测点M3下方，步序4为左线隧道掘进至监测点M4下方，步序5为左线隧道掘进到监测点M5下方，步序6为左线隧道掘进到监测点M6下方，步序7为左线隧道掘进到监测点M7下方。

由计算结果可以看出，各测点沉降变形基本上均随新建隧道的掘进而不断增加；当新建隧道掌子面通过测点时的沉降会有明显加大；下穿施工结束时，既有隧道C和D受开挖扰动较为明显，监测点M4沉降最大，沉降达到6.6 mm。

3.2 既有隧道底板测线沉降计算结果

不同施工阶段既有隧道竖向位移云图如图6、图7所示，底板沉降如图8、图9所示，横轴坐标原点即为图1中沈庄工作井位置处。根据计算结果可以看出：①当右线掘进完成后，既有结构最大沉降位置位于右线盾构隧道上部的顶管隧道D处，最大沉降值为4.3 mm；②当下穿施工完成后，其最大沉降位置向左线盾构隧道方向有所偏移，最大值为7.6 mm；③由于测线与掘进方向斜交、受双洞依次掘进以及下穿空间位置的差异等影响，各侧线沉降槽曲线均呈明显的非对称性，且有不同程度的偏转和平移；④相对于顶管隧道A、B，顶管隧道C、D受盾构区间掘进扰动较明显，累计沉降相对较大；⑤对比既有隧道底部两条测线沉降曲线可以看出，下穿施工过程中，既有隧道底板有横向不均沉降现象发生，但横向沉降差较小，均在2 mm以内，不会对通行造成影响。

图6 右线掘进完成既有隧道竖向位移云图(单位：m)

图7 施工完成既有隧道竖向位移云图(单位：m)

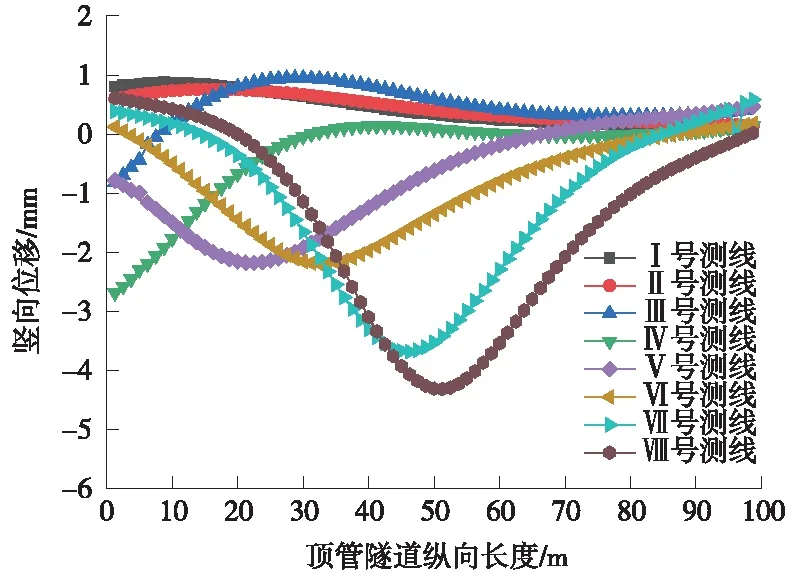
图8 右线掘进完成时各监测线沉降曲线形态

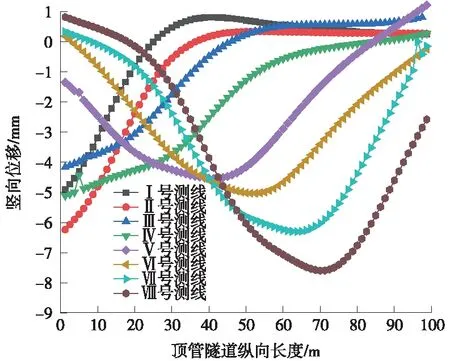
图9 施工完成时各监测线沉降曲线形态

4 既有隧道结构沉降控制基准

4.1 基本原理

(1)顶管隧道在使用过程中，接缝的张开量和管线曲率是影响隧道正常使用的重要指标，而在新建隧道下穿既有顶管隧道的施工过程中，必然会对既有顶管隧道接缝的张开量和曲率产生影响。既有顶管隧道接缝张开程度主要取决于地层沉降规律，并与顶管结构管节长度密切相关。在实际工程中，外部工程施工(4号线盾构隧道下穿施工)扰动下既有结构的变形情况可通过现场监测获取，但外部工程扰动前既有结构的变形情况比较复杂，一般难以通过实测手段获得。因此，研究中既有隧道的变形规律和数值主要取自前述三维数值模拟的结果。

(2)研究中，依据实际工程建立既有顶管隧道的有限元实体模型，模型长99 m，顶管结构采用实体单元模拟，管节长度按实际工程情况考虑，相邻管节接头节点采用非耦合方式建立，仅对沿顶管顶板中线单元节点中坐标重合的两节点进行位移(x、y、z方向)自由度耦合，模型两端施加水平位移约束，如图10所示。

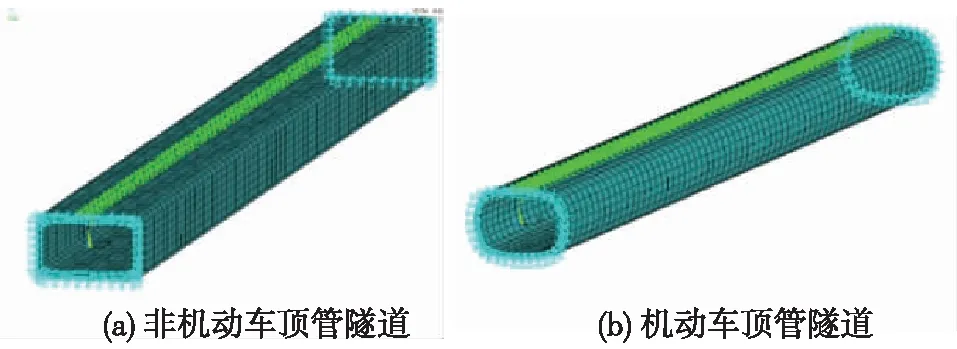
图10 既有顶管隧道结构模型

(3)下穿施工过程中，既有隧道底板响应最为敏感，并将这种扰动效应上传至顶板和侧墙。分析中，将前述三维数值模型计算得到的既有隧道地基土顶面位移结果，以位移荷载的形式施加到新建模型相应位置节点上。同时，假定既有结构底板变形规律不变，并按比例调整既有结构底板的附加竖向位移量，以此搜索既有隧道结构接头达到最大允许张开量或极限曲率时所对应的竖向允许位移值。

(4)关于既有顶管隧道结构接头允许张开量问题，目前尚无城市道路顶管隧道领域的相关技术规程和统一标准。CJJT202—2013《城市轨道交通设施结构安全技术保护规程》中规定：在外部施工作业情况下，既有顶管隧道在外部施工影响下管片张开量控制值可按表3取值。另外，也有相关研究建议柔性管道接头允许张开量应控制在3.75 mm以内[5]。

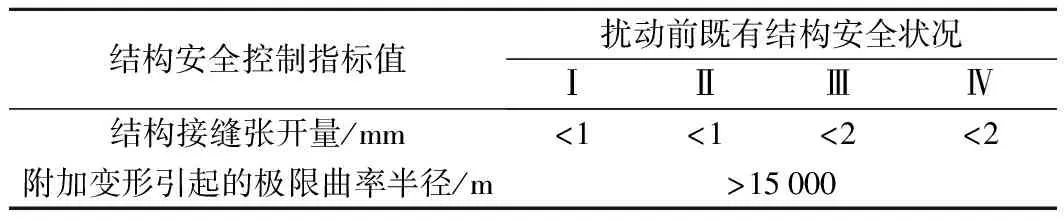
表3 盾构法或顶管法地下结构安全控制标准值

根据本工程特点，外部施工影响下的既有顶管隧道接缝允许张开量可取2 mm；既有顶管隧道附加变形引起的曲率半径允许值应大于15 000 m。

4.2 计算结果

(1)基于既有顶管接头允许张开量的沉降控制标准。

根据数值模拟计算结果，下穿施工过程中，既有顶管隧道C、D变形响应相对明显，因此，研究中分别取既有顶管隧道C、D变形结果以位移荷载的形式施加到结构模型相应的节点上。顶管隧道变形形态如图11所示。

图11 既有隧道结构变形示意

采用上述位移荷载-结构模型计算分析得出，当管节接缝张开量达到2 mm时，机动车顶管隧道底板结构所对应的沉降值为57.5 mm，非机动车顶管隧道底板沉降值为81.6 mm。

(2)基于既有隧道结构允许附加曲率的沉降控制标准。

以既有顶管隧道C、D为分析对象，比较施工完成后C、D顶管隧道4条监测线与底板中线位置处竖向位移，如图12所示。

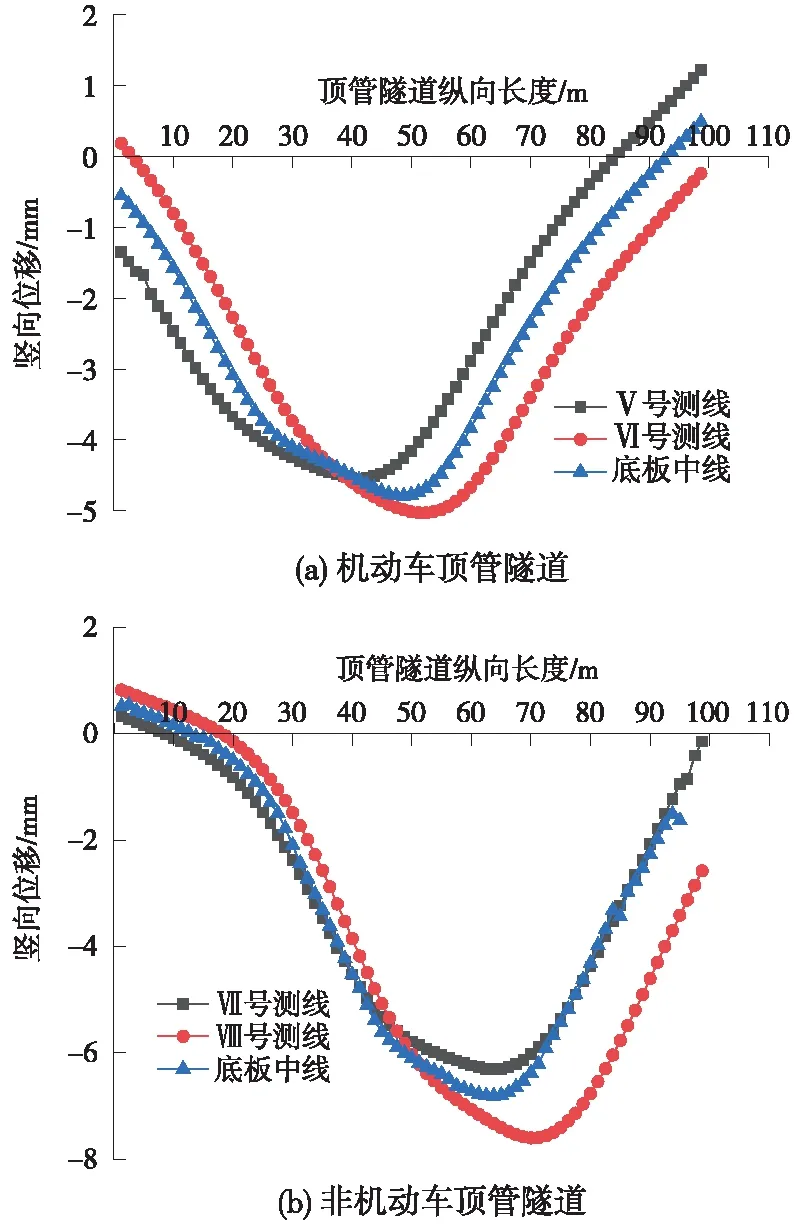
图12 既有隧道底板不同测线沉降曲线

由图12可以得出，各测线沉降曲线均呈明显的非对称性，且其最大曲率均位于最大沉降值位置。其中，Ⅵ、Ⅷ号监测线的最大沉降值、局部斜率和曲率与其他测线相比均相对较大，为精准确定曲线最小曲率半径，简化回归方程表达形式，研究中仅取Ⅵ、Ⅷ号监测线竖向位移的部分曲线作回归分析(所取曲线为最大沉降点附近一定范围的数据及图中线型相对简单的一侧数据)，并将坐标原点平移至最大沉降点位置，如图13所示。

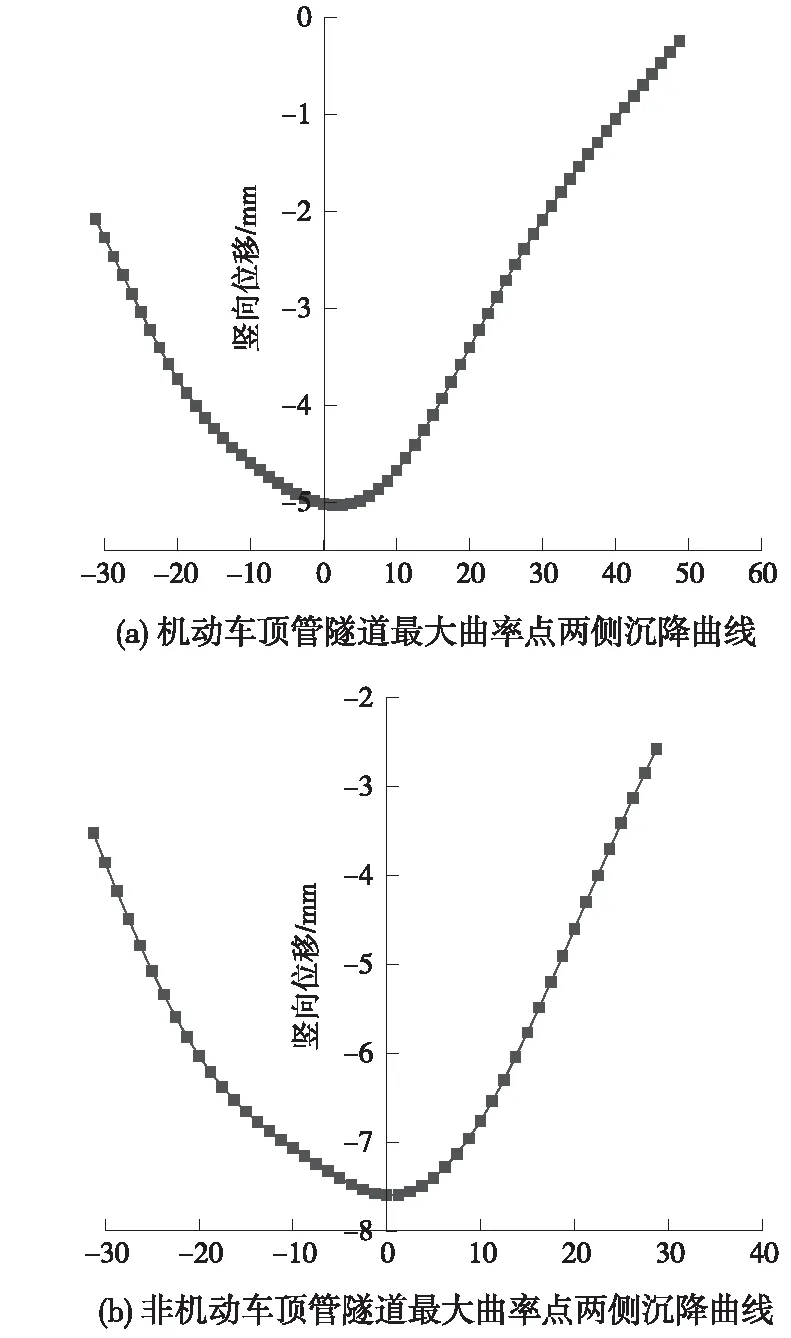
图13 既有隧道最大曲率点两侧沉降曲线

设定所得沉降回归方程符合Peck公式，机动车顶管隧道底板沉降曲线拟合如下

(1)

非机动车顶管隧道底板降曲线拟合如下

(2)

曲率半径可表示为

(3)

式中，x为距既有隧道中心水平距离，m；y为既有隧道沉降量，mm；R为曲率半径，m。

假定沉降曲线规律不变，调整最大沉降量，当最小曲率半径达到15 000 m，对应的允许最大沉降限值为：机动车顶管隧道30.9 mm，非机动车顶管隧道27.8 mm。

(3)下穿施工过程既有隧道沉降管理基准

综合上述分析结果，既有非机动车顶管隧道对沉降变形的适应性相对较差，下穿施工过程中应予以重视；相对于接缝张开量控制标准，基于既有隧道结构允许附加曲率的沉降控制要求相对较为严格。从确保施工安全角度出发，同时也为简化施工管理指标，施工中既有行车隧道和非机动车隧道均采用统一的最大沉降控制限值，即允许最大沉降不应大于25 mm，预警值均按允许最大沉降的50%设置，即12.5 mm。

5 监测结果

为保证施工安全，在下穿段影响范围内既有顶管隧道底板布设了监测点，测点具体布置如图14所示。

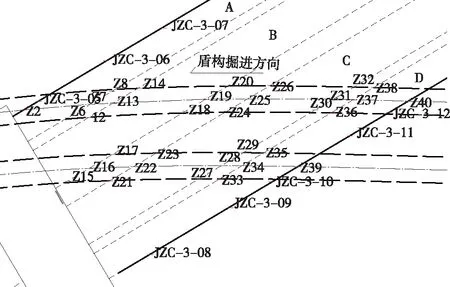
图14 现场监测点布置

施工结束后既有顶管隧道C、D结构底板测线沉降的实测与数值计算结果分别如图15、图16所示，从图中可得：①数值模拟结果略小于现场监测结果，但两者规律性吻合较好，证明基于数值计算结果建立的沉降控制标准是切实可行的；②施工过程沉降控制效果较好，累计沉降远小于所制定的预警值。

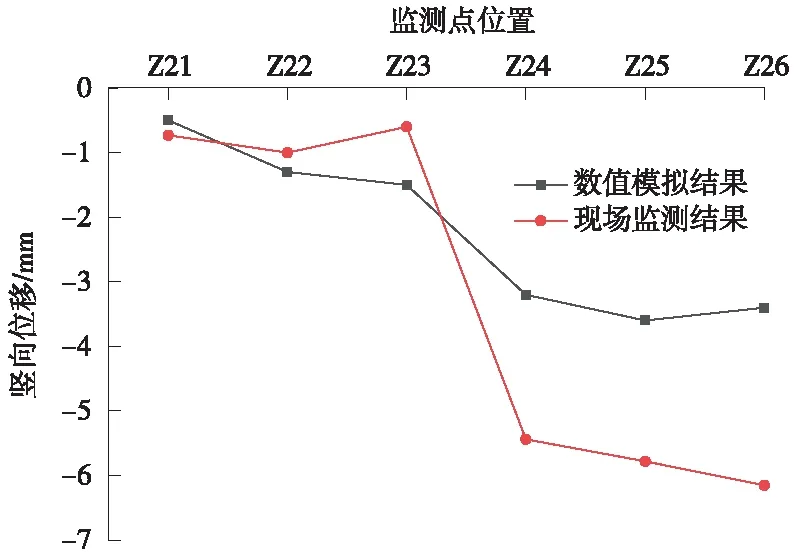
图15 C顶管隧道沉降曲线

图16 D顶管隧道沉降曲线

6 结论

以郑州地铁4号线会展中心站—商鼎路站区间盾构下穿既有顶管隧道群为工程背景，开展了地铁盾构隧道近距离下穿既有顶管隧道施工力学效应及变形控制基准研究，主要结论如下。

(1)三维数值动态模拟计算揭示了下穿施工过程中既有顶管隧道结构变形规律和形态特征：受隧道空间位置关系及盾构双洞依次掘进影响，顶管隧道轴向沉降曲线均呈明显的非对称性，且在施工过程中发生不同程度的偏转和平移；相对于顶管隧道A、B，顶管隧道C、D受盾构区间掘进扰动较明显，累计沉降相对也较大；对比同一顶管隧道底部两侧测线沉降曲线可以看出，下穿施工过程中，隧道底板有横向(垂直于通行方向)不均沉降现象发生，但沉降差较小，均在2 mm以内，不会对通行造成影响。

(2)提出了以数值模拟为基础、以隧道管节接缝允许张开量和结构线形允许最小附加曲率半径为控制目标的顶管隧道沉降控制标准确定方法；从确保施工安全角度出发，施工中既有行车隧道和非机动车隧道均采用统一的沉降控制限值，即允许最大沉降不应大于27 mm，预警值均按允许最大沉降的50%设置，即13.5 mm。

(3)现场监控量测证实了基于数值结果建立的沉降控制标准的可靠性，且施工沉降控制效果较好，累计沉降远小于所制定的预警值。

提出的沉降控制标准及其确定方法主要是基于实际工况制定的，后续可对正交下穿、上跨等不同穿越情况下顶管隧道的变形特点进行研究，拓宽沉降控制标准制定方法的应用范围。