小直径冷衬复合管过盈配合力学研究
2022-03-22黄邵军邓记松董元平
黄邵军,邓记松,董元平
(海洋石油工程股份有限公司,天津 300452)
由于海洋气候的特殊防腐要求,海洋平台上的复合板制压力容器应用广泛。复合板制压力容器小管径接管(DN≤50 mm)的堆焊施工难度较大、效率低。海洋平台高压设备多采用不锈钢冷衬管代替小管径堆焊,以降低设备制造费用及周期【1】。然而,目前针对不锈钢复合管冷衬工艺过盈量的研究较少,工程上多根据经验进行制造。有学者【2-3】基于弹性理论分析推导了反应堆压力容器封头与管座过盈装配时的过盈量计算公式。其他类似的研究多集中在轮轴模型的过盈配合【4-7】,或典型的圆柱面过盈配合【8-9】,但其与压力容器的受力特点显著不同。作为受压元件,在内压作用下,其过盈配合在结合面引起的应力集中较大,容易萌生裂纹【10】。
针对典型的小直径冷装复合管,本文通过弹性理论分析分别推导出装配状态和内压作用时最小过盈量的解析解,并以某海洋平台实际工程项目为例,通过有限元软件ANSYS分析不同过盈量对冷衬复合管的应力影响,得出其接触压力及应力强度的分布规律,以供工程应用参考。
1 不锈钢冷衬复合管结构特点
某海洋平台复合板制低温设备,设计压力11 MPa,直径1 400 mm,设计温度-28 ℃,壳体基材为16MnDR,壁厚50 mm,内部堆焊3 mm厚的S31603覆层。设备上DN50的接管受制于较小的内径和较长的接管外伸长度,若采用堆焊施工难度较大且工期长,同时也不利于焊后检测,因此采用不锈钢管冷衬工艺。图1中所示接管采用安放式结构,接管与筒体焊接完成后,首先进行精加工以保证孔的精度;精加工完成后,用液氮对不锈钢管进行冷却,并计算冷却时间,以获得合适的过盈量【11】;然后将不锈钢管插入接管后,再与法兰端面以及筒体堆焊层进行密封焊。本案例由于是低温设备,按照GB/T 150—2011相关规定,其筒体开孔内壁需倒圆角,在实际项目施工时,内衬不锈钢管需内伸至圆角过渡处以上5 mm左右(见图1),然后堆焊至筒体复合板层。
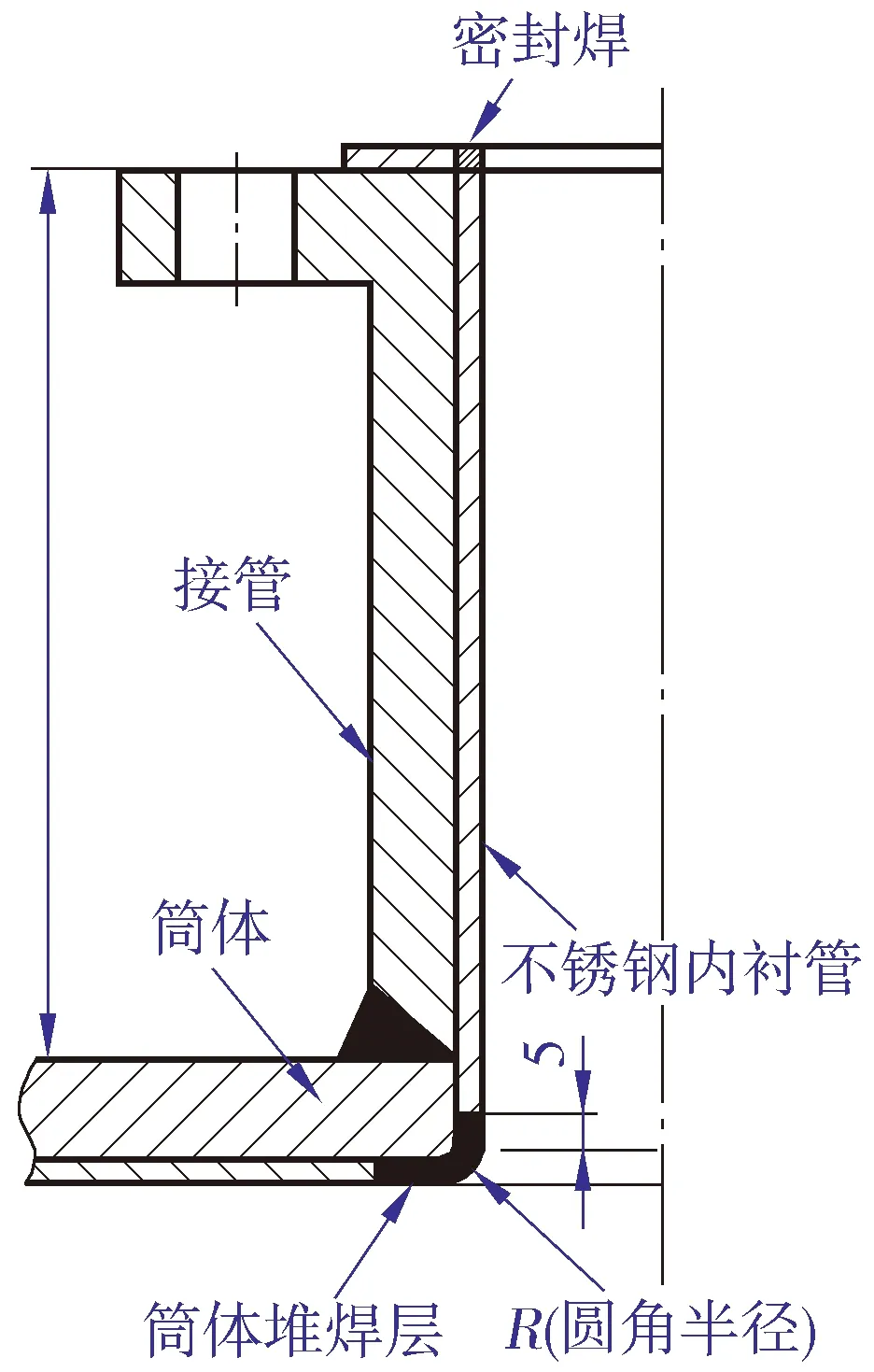
图1 冷衬复合管结构示意
2 过盈配合的弹性力学解
内衬不锈钢管与基层接管的过盈配合在结合面产生接触应力,不考虑轴向边界条件的情况下,其受力处于二向应力状态。如图2所示,将接管简化为承受内壁压力的圆筒、内衬不锈钢管简化为仅承受外壁压力的圆筒。根据弹性力学,采用厚壁圆筒理论可以求出接管和内衬不锈钢管的径向和周向应力【6,12】。由于不锈钢和碳钢两种材料的弹性模量与泊松比几乎相同,为简化工程计算,在公式中不作区分。
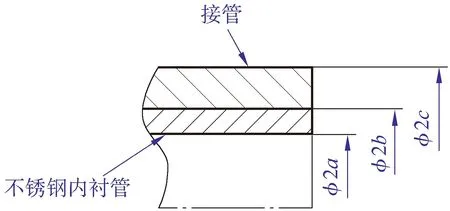
图2 冷衬复合管力学模型简化
首先,根据过盈量和装配后的变形协调确定结合面接触压力p0:
(1)
式中:p0——接触压力,MPa;
E——材料的弹性模量,MPa;
δ——基材接管与内衬不锈钢管装配的过盈量,mm;
a——内衬不锈钢管的内半径,mm;
b——内衬不锈钢管的外半径,mm;
c——基材接管的外半径,mm。
内衬不锈钢管的径向应力σr1和周向应力σθ1分别如下:
(2)
式中:σr1——内衬不锈钢管的径向应力,MPa;
r——基材接管或内衬不锈钢管任意位置的半径,mm。
(3)
式中:σθ1——内衬不锈钢管的周向应力,MPa。
基材接管的径向应力σr2和周向应力σθ2分别如下:
(4)
式中:σr2——基材接管的径向应力,MPa。
(5)
式中:σθ2——基材接管的周向应力,MPa。
2.1 最小过盈量的计算
接管在承受内压和外载荷时会产生轴向的拉脱力。为使内衬不锈钢管不出现滑脱现象,由过盈配合提供的摩擦力应大于内压及外载荷产生的拉脱力。
1)水压试验工况下,内衬不锈钢管承受的拉脱力FTT为:
FTT=ptπa2
(6)
式中:FTT——水压试验工况下内衬不锈钢管承受的拉脱力,N;
pt——水压试验压力,MPa。
2)设计工况下,接管承受的外载荷弯矩按照文献【13】等效为当量内压pe:
(7)
式中:pe——当量内压,MPa;
M——接管承受的总弯矩,N·mm。
由式(7)可得,设计工况下冷衬不锈钢管承受的总轴向力F轴为:

(8)
式中:F轴——设计工况下冷衬不锈钢管承受的总轴向力,N;
pD——设计压力,MPa;
FX——接管承受的轴向力,N。
扭矩在过盈结合面产生的周向力F周为:

(9)
式中:F周——过盈结合面产生的周向力,N;
MT——接管承受的扭矩,N·mm。
设计工况下承受的最大拉脱力FTD为:
(10)
式中:FTD——设计工况下承受的最大拉脱力,N。
最大拉脱力FT为:
FT=max(FTT,FTD)
(11)
式中:FT——最大拉脱力,N。
由过盈配合提供的摩擦力Ff为:
Ff=2p1πalfu
(12)
式中:Ff——过盈配合提供的摩擦力,N;
p1——最大拉脱力对应的设计压力或试验压力,MPa;
lf——过盈配合的轴向结合面长度,mm;
u——过盈结合面的摩擦系数。
摩擦力应不小于由内压轴向力产生的拉脱力,即
Ff≥FT
(13)
由此可得结合面最小压力pmin:
(14)
式中:pmin——结合面最小压力,MPa。
代入式(1)可得最小过盈量δmin为:
(15)
式中:δmin——最小过盈量,mm。
2.2 操作工况下最小过盈量的修正
内衬不锈钢管在装配工况不受内压的情况下可按式(1)计算结合面的压力。操作工况下,内衬不锈钢管由于承受操作压力,故过盈量不再是装配状态下的值。其外径压缩量变小,径向伸长量δ1按式(16)计算:
(16)
式中:δ1——内衬不锈钢管的径向伸长量,mm;
E1——内衬不锈钢管的弹性模量,mm;
μ1——内衬不锈钢管的泊松比。
基层接管在承受内压时,内压引起的径向伸长量δ2按式(17)计算:
(17)
式中:δ2——基层接管的径向伸长量,mm;
E2——接管的弹性模量,mm;
μ2——接管的泊松比。
因此,由内压引起的过盈增加量Δδ按式(18)计算:
Δδ=2(δ1-δ2)
(18)
式中:Δδ——内压引起的过盈增加量,mm。
考虑内压后的最小初始过盈量δmin1为:
(19)
式中:δmin1——考虑内压后的最小初始过盈量,mm。
3 过盈配合的弹性数值分析
由于接管、衬管与筒体焊接的结构不连续性,仅采用理论计算无法准确分析其接触特性,因此,本文采用有限元分析软件ANSYS对小直径冷装复合管进行数值分析。建立5组不同过盈量的有限元模型,具体参数见表1。其中,基层接管与内衬不锈钢复合管的接触采用摩擦接触算法,接触区域网格大小进行适当加密,摩擦系数参考文献【14】取0.2。
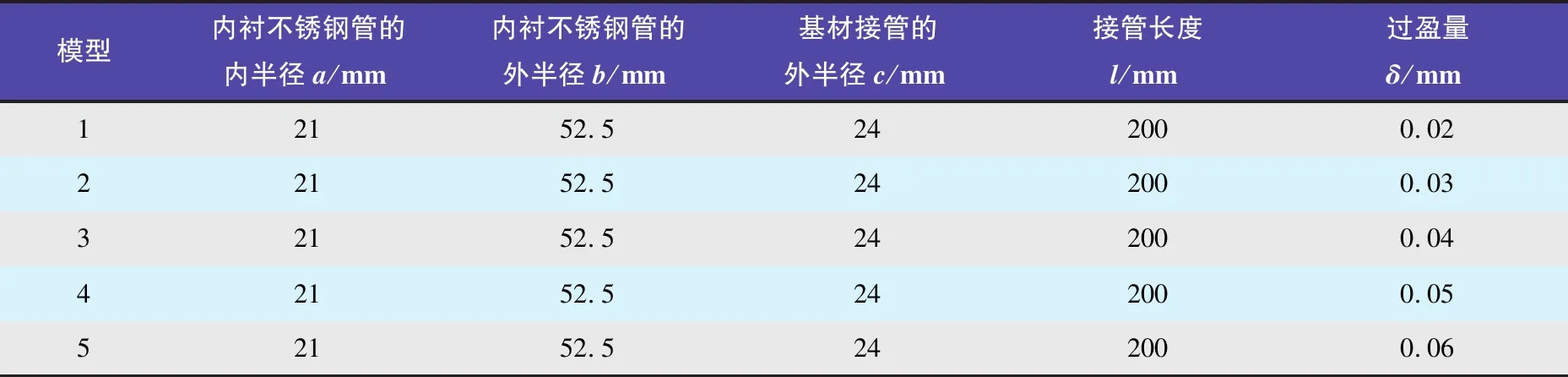
表1 5组不同过盈量的模型主要参数
为同时考虑冷装配和操作工况,本文采用生死单元法,分2个载荷步加载,第一个载荷步将与冷衬管焊接的密封面及堆焊层的单元状态设置为DEAD,仅计算冷装配工况;第二个载荷步时激活杀死的单元,同时加载内压模拟操作工况。
筒体采用局部模型,对称面进行对称约束;接管及筒体内部加载内压;接管端部加载等效应力;筒体轴向一端加载等效应力,另一端在柱坐标系下约束轴向位移和环向位移。其有限元模型如图3 所示。
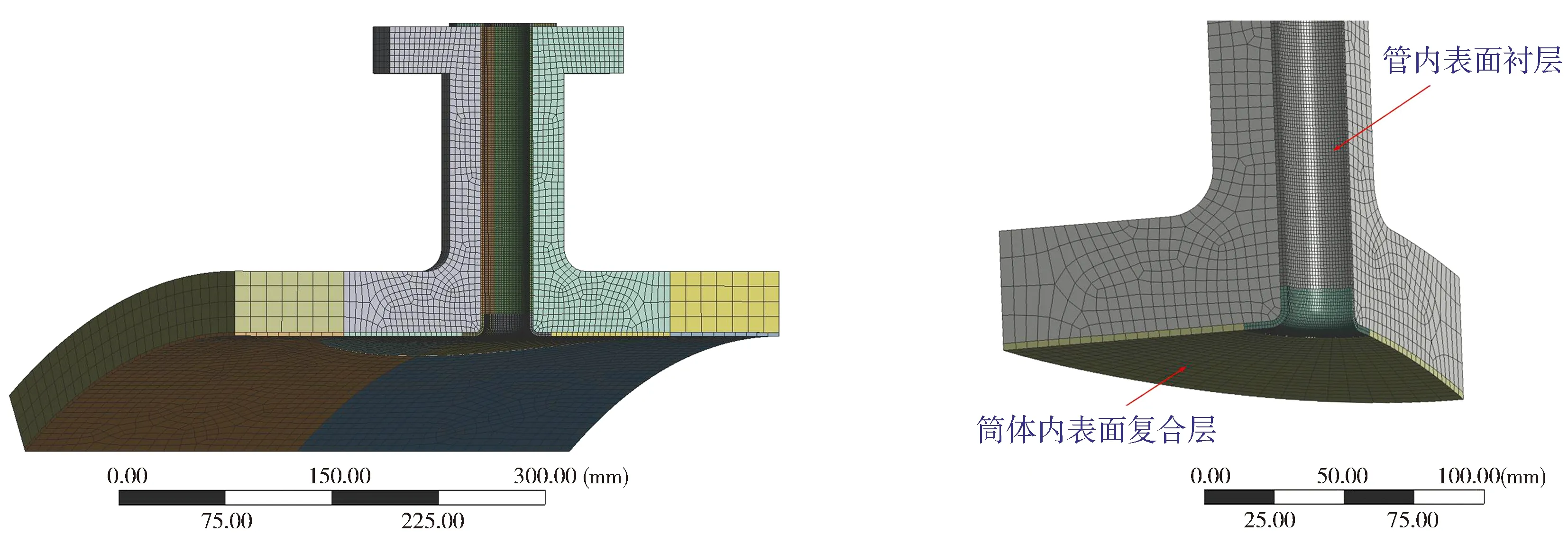
图3 有限元模型
3.1 冷装配状态下和内压状态下的接触压力分布
对5组不同过盈量的模型进行有限元仿真分析。通过改变冷衬不锈钢管与接管之间的过盈量,得出在不同过盈量情况下的接触压力分布,并将有限元计算的平均接触压力与式(1)计算的理论结果进行了对比,见表2。由表2可见,5组不同过盈量情况下有限元仿真计算结果与理论值的误差均在5%之内。这是由于实际的接管模型并不是理想的长圆筒与轴的过盈配合模型,其平均接触压力受到筒体和法兰的影响。但是理论计算误差仍在工程允许范围内。
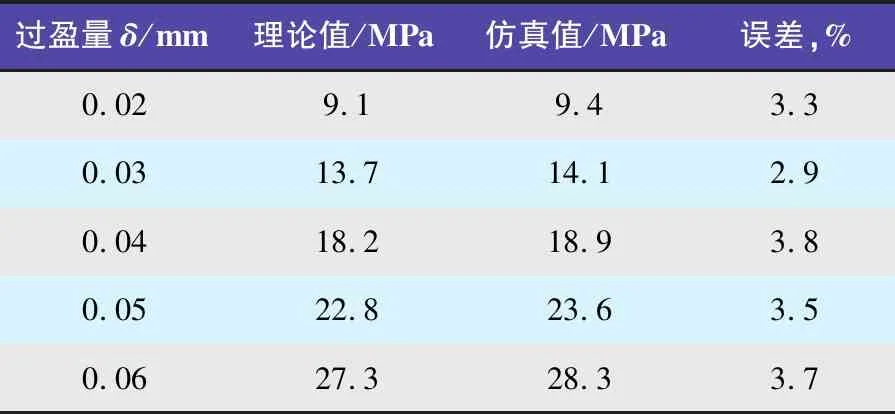
表2 不同过盈量的接触压力对比
以表1中的模型3为例进行计算。在冷装配状态下,接管与冷衬不锈钢管的接触压力分布在沿衬管长度上较为均匀,如图4所示;在承受11 MPa 内压状态下,冷衬管最底端接触压力接近为0,在筒体开孔范围内沿冷衬管的轴向逐渐增加,在远离接管开孔处均匀分布,并达到最大的接触压力,如图5所示。这是由于筒体受压后,开孔处在筒体环向应力作用下,径向位移量较大,原来的圆形开孔趋于椭圆形,使得冷衬管的过盈量减小。筒体接管开孔处的应力分布见图6,其最大值位于筒体环向截面。
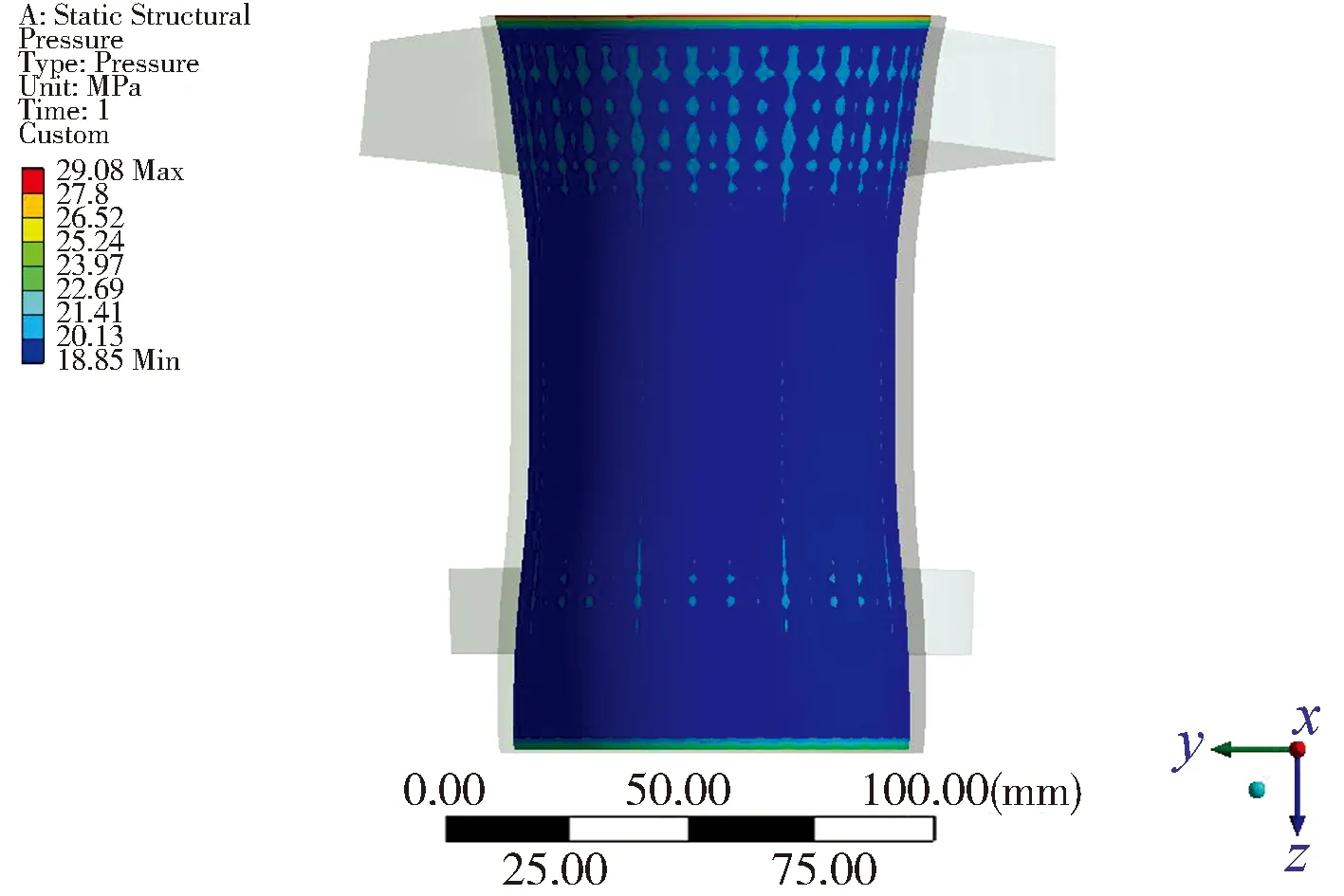
图4 冷装配状态下接管与冷衬管的接触应力分布
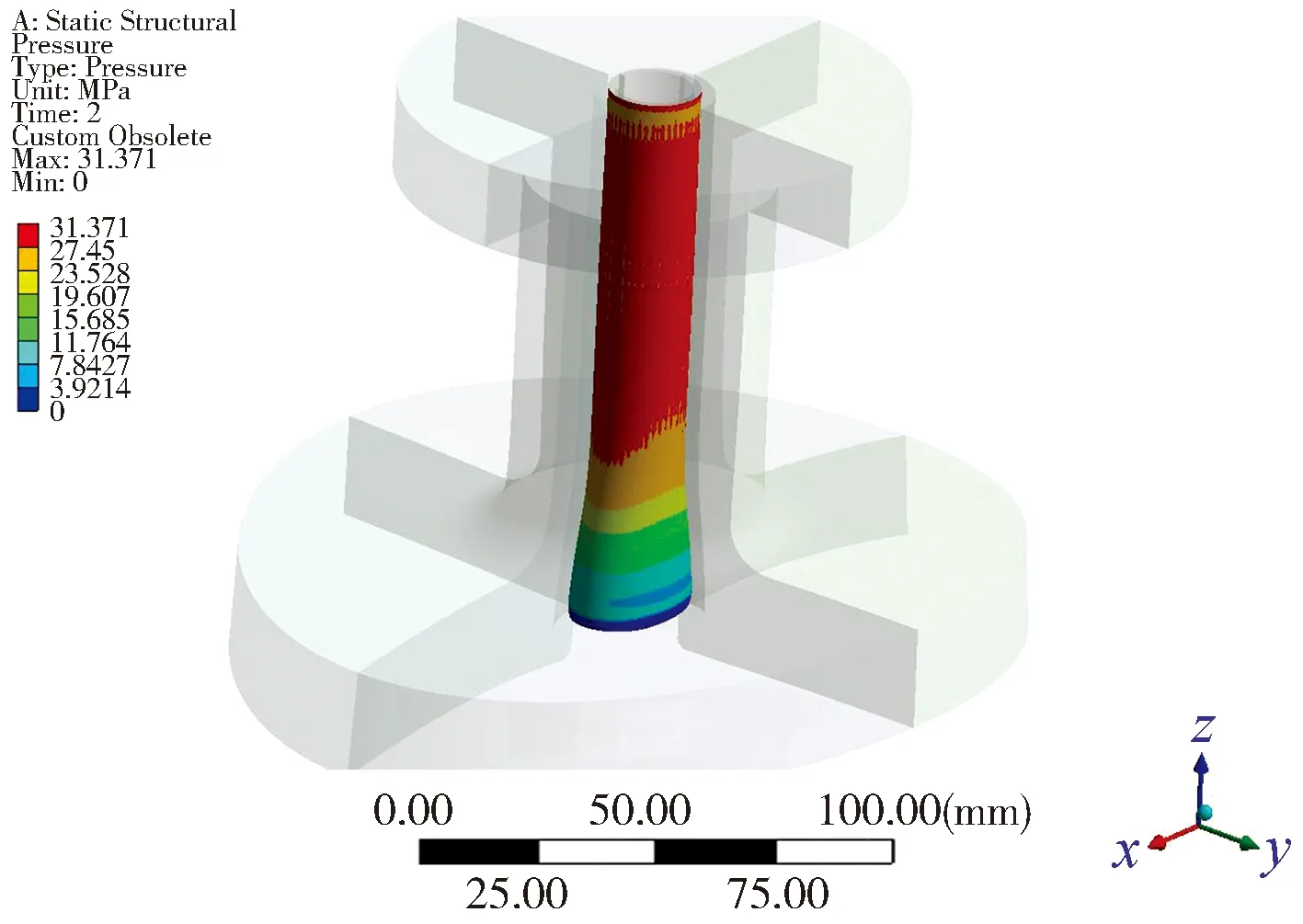
图5 内压状态下接管与冷衬管的接触应力分布
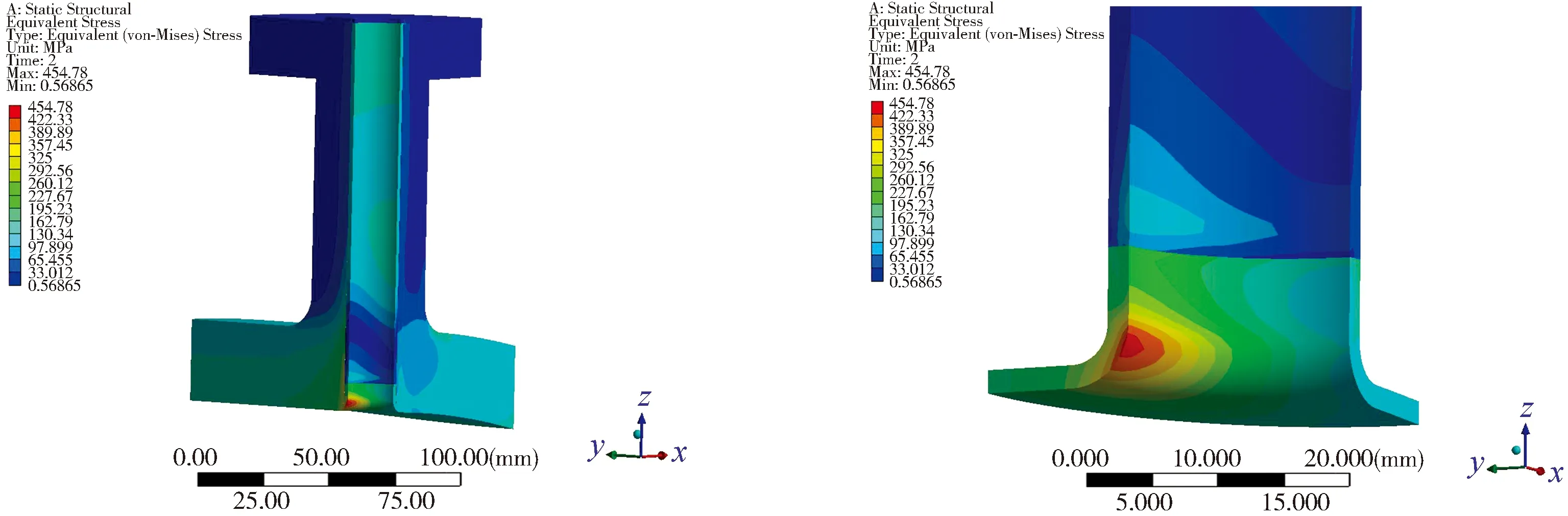
图6 内压状态下接管及衬管应力分布云图
3.2 冷装配状态下的应力强度分布
在保持尺寸等其他条件不变的情况下,选取表1中的5组不同过盈量建立有限元模型进行对比计算。图7是5组过盈量下接管在过盈配合面的应力强度沿接管长度的分布规律,其横坐标原点为与筒体堆焊面焊接的冷衬不锈钢管端部。由图7可见:接管应力强度随着过盈量的增加而增加,且不同过盈量接管应力强度的分布规律几乎一致;在接管根部由于受到筒体的加强,其应力强度最小;在靠近法兰的接管端部,接管得到法兰的加强,应力强度呈下降趋势;接管中间位置应力强度最大,且接近均匀分布。
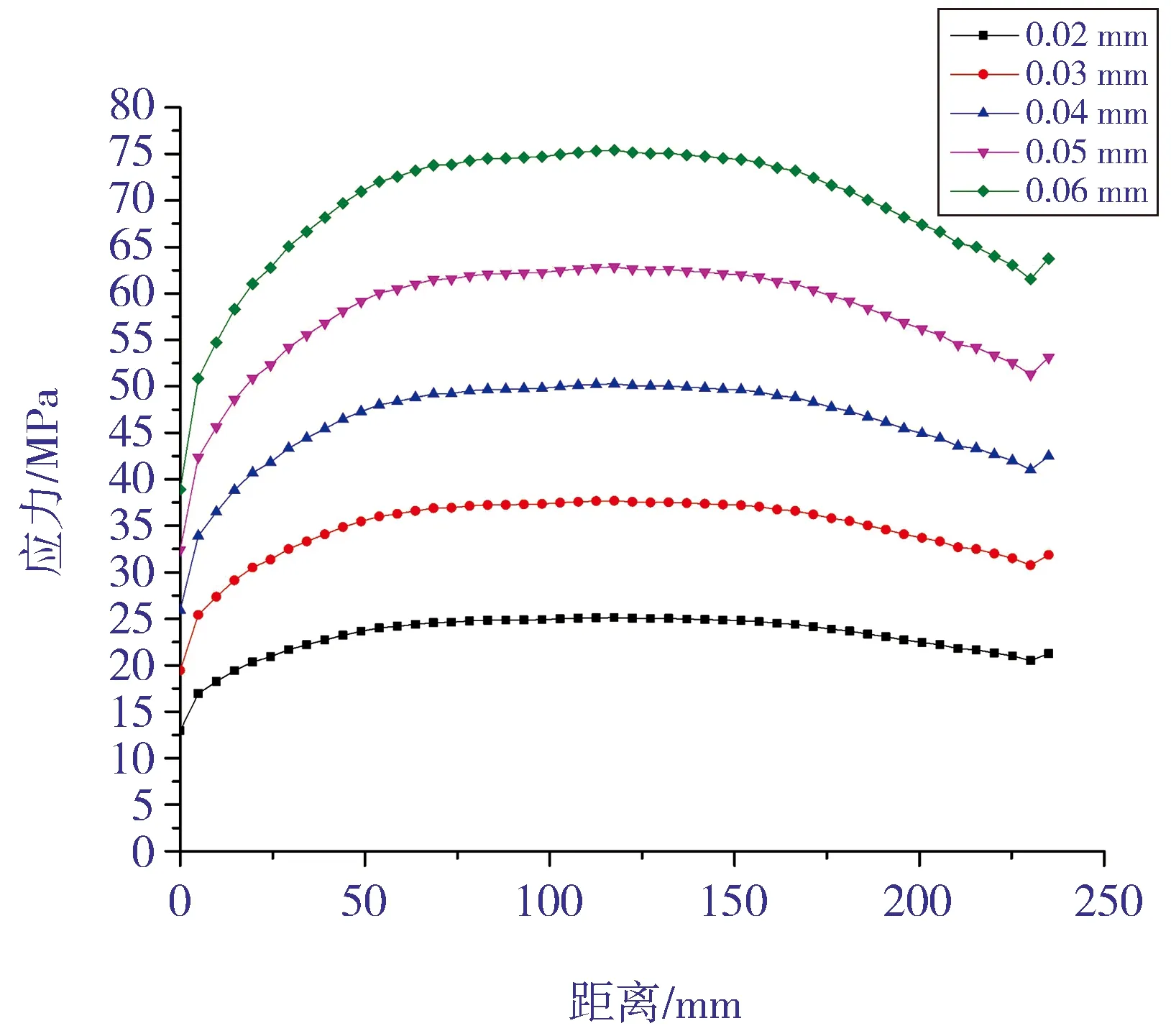
图7 冷装配状态下接管过盈配合面的应力强度分布
图8是5组过盈量下冷衬不锈钢管在过盈配合面的应力强度沿接管长度的分布规律。由图8可见:不同过盈量冷衬不锈钢管应力强度的分布规律也几乎一致,在根部应力强度最大;中间位置应力强度减小且接近均匀分布;在靠近法兰的接管端部,其应力强度增加,应力值大小接近根部。在同一过盈量下,由于冷衬不锈钢管的壁厚只有3 mm,故由过盈产生的应力强度远大于接管。因此,对于冷衬不锈钢复合管,在冷装配状态下,因过盈量过大而引起的强度失效一般发生在冷衬不锈钢管上。
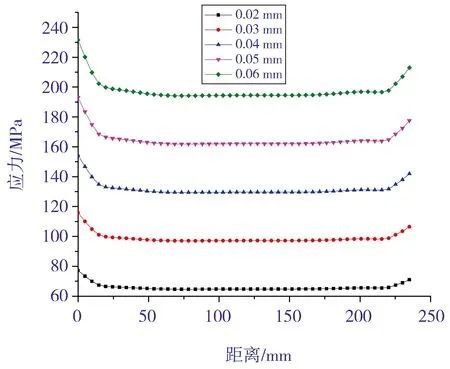
图8 冷装配状态下内衬不锈钢管过盈配合面的
3.3 内压作用下的应力强度分布
压力容器在试压或操作状态下,不仅承受冷衬复合管在过盈配合作用下产生的装配应力,还会叠加由于内压产生的应力。为研究内压作用下冷衬复合管过盈结合面的应力分布情况,本文首先计算了设计压力下不同过盈量的应力强度,其分布情况如图9及图10所示。由图9和图10可见:接管的应力强度均随过盈量的增加而增加;不锈钢冷衬管在筒体开孔附近受开孔变形的影响,应力强度均较小,并呈现出先下降再上升的复杂状态,后面随过盈量的增加而显著增加。
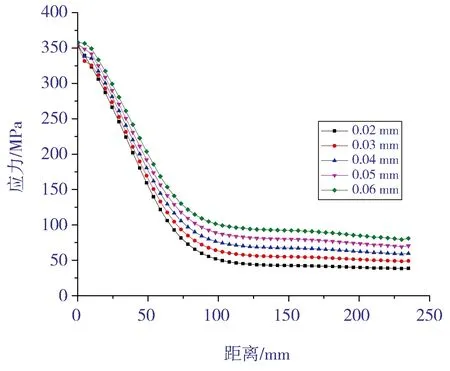
图9 设计压力下接管过盈配合面的应力强度分布
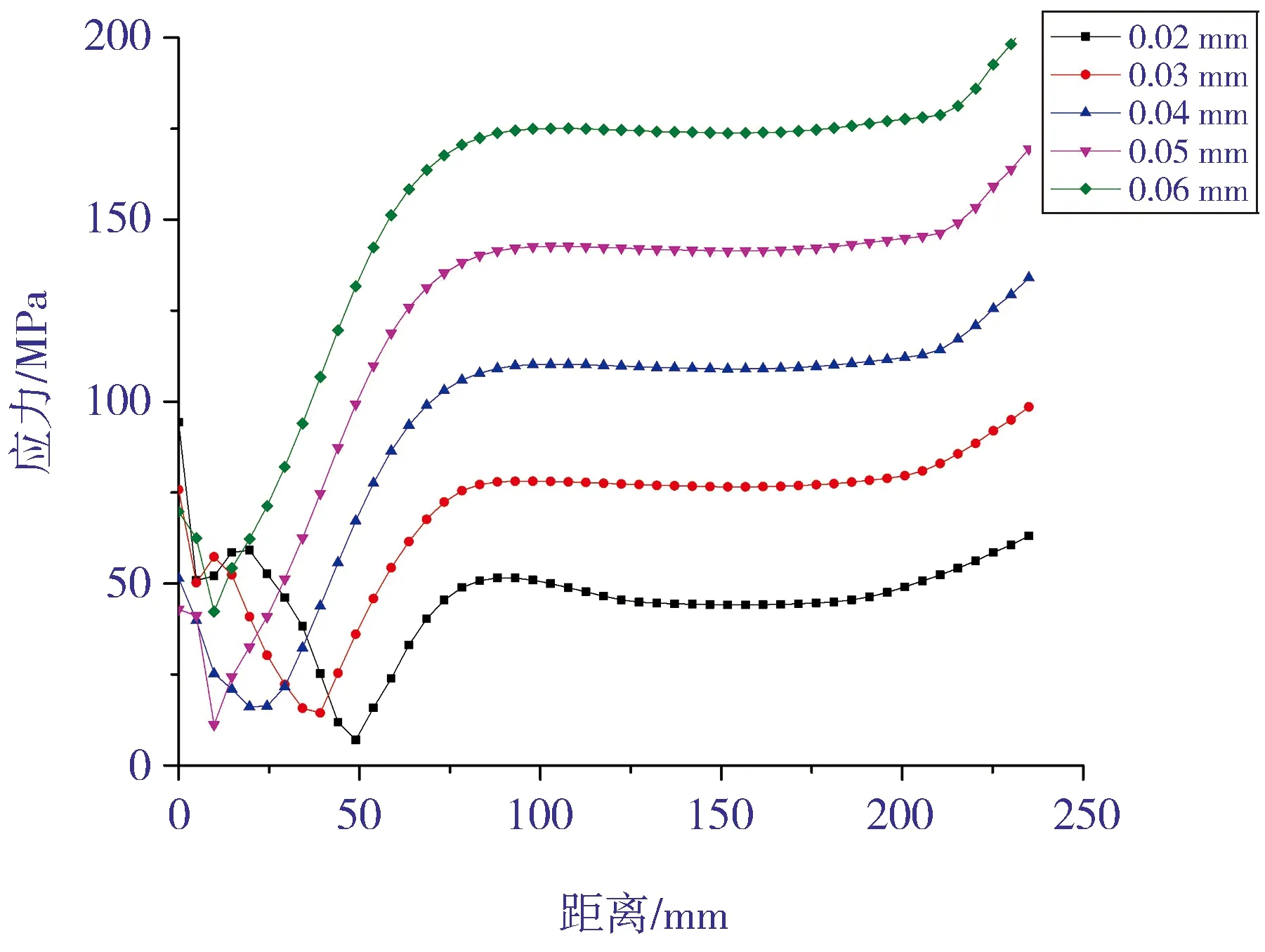
图10 设计压力下内衬不锈钢管过盈配合面的
其次,本文取表1中过盈量为0.04 mm的案例,在其他参数保持不变的情况下,分别加载2、5、8和11 MPa的内压进行对比计算,结果见图11 和图12。由图11可知,随着加载内压的增大,接管的应力强度也逐渐增大。对比图7和图9可知,内压状态下接管开孔处应力强度最大,而冷装配状态下接管开孔处的应力强度最小。由图12可知,随着加载内压的增大,内衬不锈钢管的应力强度逐渐减小。这是由于在冷装配状态下,内衬不锈钢管承受的应力为压缩应力,之后施加的内压抵消了一部分压缩应力。
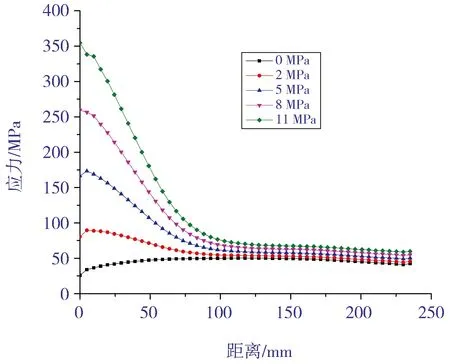
图11 内压作用下接管过盈配合面的应力强度分布
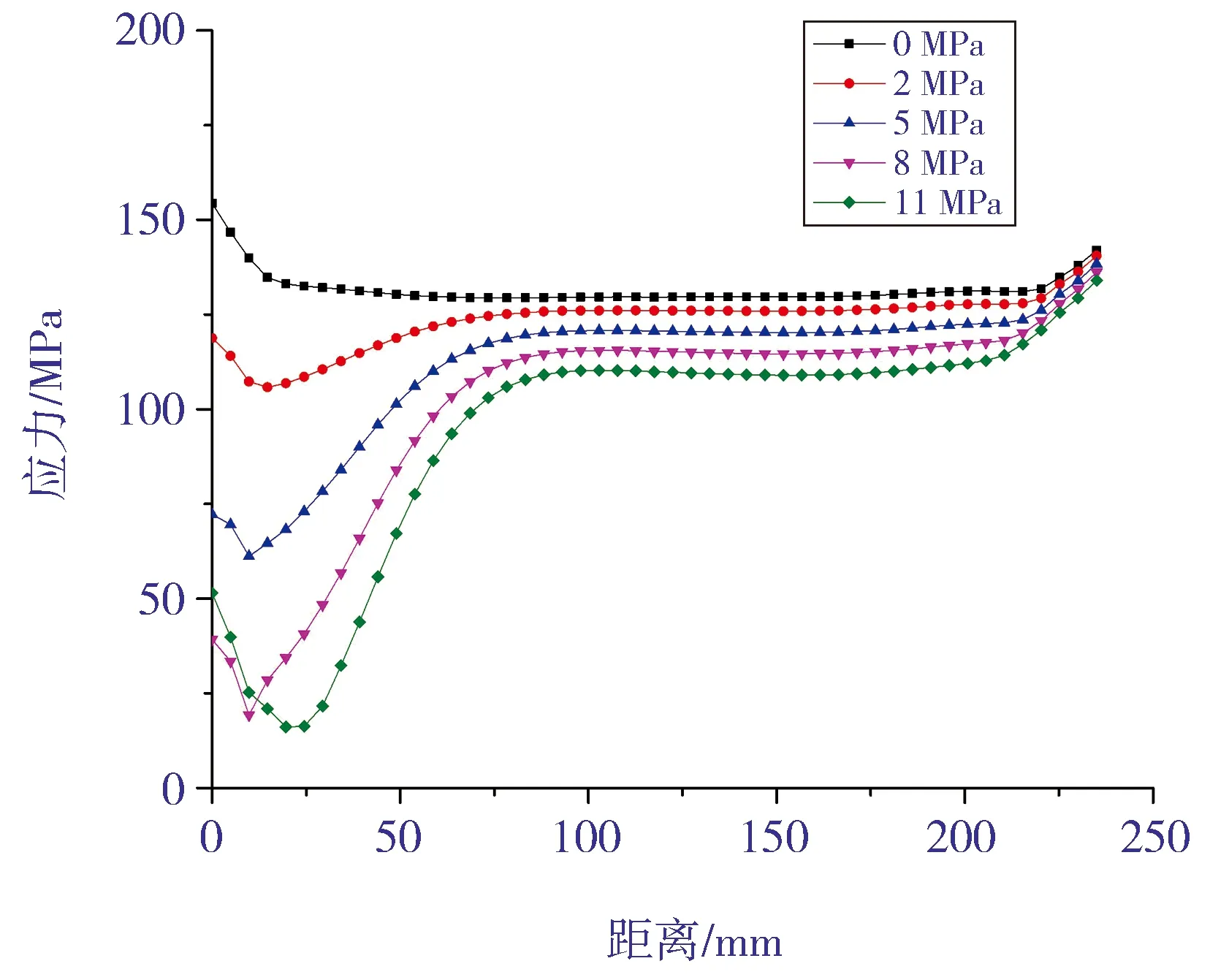
图12 内压作用下内衬不锈钢管过盈配合面的
4 结语
1)根据弹性力学厚壁圆筒理论得出了内压作用下最小过盈量的解析计算公式,并通过5组不同过盈量的有限元模型进行计算对比,结果显示,接触压力的仿真值与理论计算的误差在5%以内,证明理论计算公式可以用于工程实践。
2)冷装配状态下,接触压力在冷衬管上接近均匀分布;内压状态下,由于受到筒体开孔变形的影响,接触压力在筒体开孔附近较小,在远离开孔部位呈均匀分布。
3)在冷装配状态下,衬管由于壁厚较薄,其应力强度一般大于接管的应力强度,故失效首先发生在冷衬不锈钢管上。
4)在操作或试压状态下,随着内压的增加,接管的应力强度不断增加,而不锈钢衬管的应力强度不断减小。因此,对于冷衬管而言,相比操作工况,冷装配工况引起的应力强度更大。
