二维不均匀风速分布对大型空气源热泵蒸发器性能影响的研究

张 鑫 姚海清 侯 幸 张文科 崔玉萍

（1.山东建筑大学热能工程学院 济南 250101；2.山东中瑞新能源科技有限公司 济南 250101）

0 引言

翅片管换热器是空气源热泵的重要部件，是紧凑型换热器中应用最广泛的一种，其传热过程不仅要考虑管内侧制冷剂的沸腾或冷凝，还要考虑翅片侧的空气结露结霜，整个过程较为复杂。冬季制热运行时，翅片管换热器作为蒸发器，其性能直接影响到空气源热泵的整体性能，因此对翅片管换热器性能优化分析意义明显。

以往对翅片管换热器的研究主要集中在管内和管外结构以及可替代的高效、环保制冷剂的寻找[1]，而忽略了翅片管换热器整体换热温差的影响，且对流路布置的研究较少。空气侧送风速度的均匀性、制冷剂侧质量流量的均匀性以及管与管通过翅片的导热都会因为流路布置的不同而影响翅片管换热器的性能。

目前，大型空气源热泵的翅片管换热器尺寸较大，长度能达到一米甚至更长，其布置方式多采用V、W 等字型。风机被设置于顶部，尽管为了保证风速的均匀性采用了吸入式风机，但风机的数量和安装位置以及其他因素必然会导致风速的不均匀，因此在努力降低风速的不均匀性的同时，研究对风速均匀性不敏感的流路布置，降低风速分布对换热器性能的影响。黄东、李权旭等人利用EVAPCOND 软件，分析了风速均匀分布以及风速呈上三角、下三角、中三角分布对翅片管换热器的性能的影响[2,3]。张春路等人研究了4 种典型的不均匀风速分布形式和风速不均匀度对空气源热泵冷凝和蒸发两用翅片管换热器性能的影响[4]。

但是，目前已有的模拟研究大多只考虑了风速分布沿翅片管竖直方向的一维不均匀性，忽略了沿管长方向的不均匀性，而综合考虑风速分布的二维不均匀性更符合实际情况，所以对二维不均匀性的分析尤为重要。本文通过建立翅片管换热器的分布参数模型，以分别采用制冷剂R410A 及R22 的蒸发器为被研究对象，分析了在不同二维不均匀风速分布情况下蒸发器的性能变化。

1 传热模型的分析

1.1 模型的建立

以蒸发器翅片管换热器为研究対像，建立蒸发器的传热模型。为了计算每根管的换热性能、不同结构对换热器性能的影响等，采用分布参数模型，把换热器划分为多根管及其范围内的翅片，每根管及其范围内的翅片又可再划分为多个微元控制体，如图1所示，其中X 方向为翅片管换热器深度方向，Y 方向为管长方向，Z 方向为竖直方向。然后，对每个微元控制体按照集总参数法建模，引入能准确描述流路布置的图论方法[5]，并添加一个二维矩阵用来描述迎风面第一排管的风速分布。

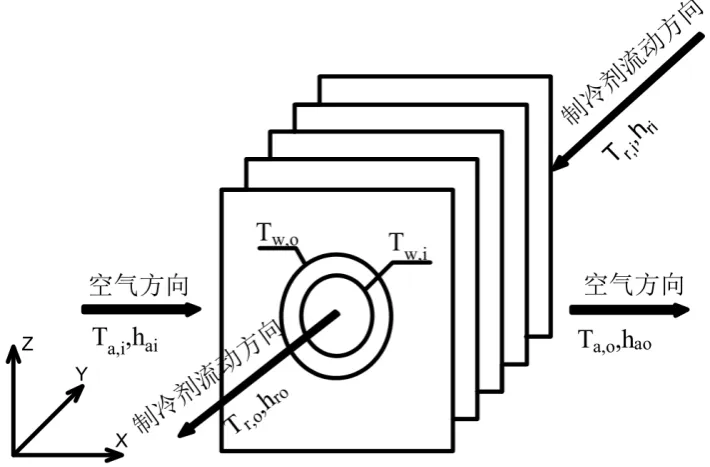
图1 微元控制体示意图Fig.1 Schematic diagram of micro element control volume

为了使数学模型方便推导和分析，设定相应的前提条件如下所示：

（1）传热仅沿管径向进行，忽略轴向传热。

（2）制冷剂在管内，只考虑轴向运动，忽略径向运动。

（3）不考虑蒸发器的结霜工况。

（4）空气被认为是不可压缩流体，且垂直于制冷剂流动方向作一维流动。

（5）暂不考虑管与管之间的传热。

每个微元体包括三部分传热过程：

（1）制冷剂与管壁之间的对流换热，其基本控制方程：

式中，Qr为制冷剂侧换热量，W；mr为制冷剂质量流量，kg/s；hri、hro分别为制冷剂进出口焓值，J/kg；Ai为微元体内换热管内表面积，m2；αr为制冷剂侧传热系数，W·m-2·K-1；制冷剂侧分为两相区与单相区，两相区传热系数的计算可以采用Jung-Radermacher 关联式[6]，单相区中传热系数采用Dittus-Boelter 关联式[7]。

ΔT1(2),r=Tr,i(o)-Tw,i(o)，Tr,i、Tr,o分别为制冷剂进出口温度，K；Tw,i、Tw,o分别为管道内外壁温度，K。

（2）管与翅片之间的导热，对应的传热方程如公式（2）所示：

式中，k为管道导热系数，W·m-1·K-1；L为管段长度，m；di、do分别为管道内外径，m。

（3）空气与管和翅片之间的对流换热方程如公式（3）和（4）所示：

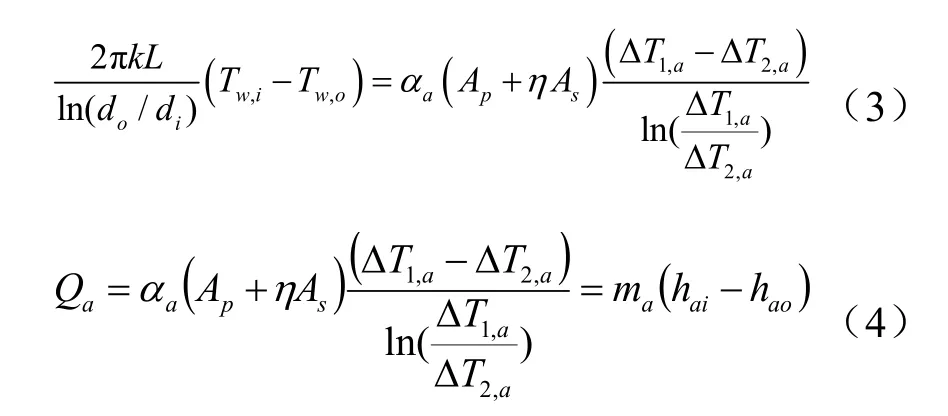
式中，αa为空气侧对流传热系数，W·m-2·K-1；对于百叶窗翅片，可以采用C C Wang 的关联式计算[8]。Ap、As分别为管道外表面积和翅片表面积，m2；hai、hao分别为空气进出口焓值，J/kg；ΔT1(2),a=Ta,i(o)-Tw,i(o)，Tr,i、Tr,o分别为空气进出口温度，K。

η为翅片效率，计算公式如公式（5）所示[9]：

式中，mhf为无因次肋高，m=√(2αa/λfδf)，λf为翅片材料导热率，W·m-1·℃-1；hf和δf分别为翅片高度和厚度，m。

除了微元控制体的能量平衡，还需要考虑制冷剂侧的压降：

式中，Δpf是摩擦压降，单相区采用Churchill的关联式[10]，两相区采用Friedel 的关联式[11]。Δpa为加速压降[5]，只考虑两相区，单相区忽略加速压降：

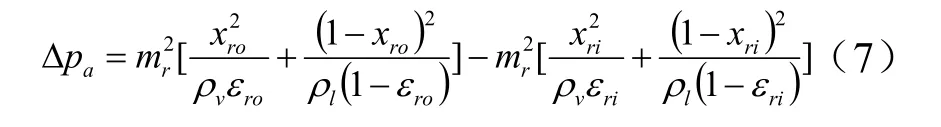
式中：mr为制冷剂质量流量，kg/h；xri、xro分别为制冷剂进出口干度；ρl、ρv分别为制冷剂液态和气态的密度，kg/m3；εri、εro分别为制冷剂进出口的空泡率。

1.2 模型的验证

采用本文建立的传热模型，依照Domanski 等人实验的结构及运行参数进行计算，并将结果与Domanski 等人的实验数据进行对比[12]。以R22 和R410A 制冷剂为例，基于夏季空调工况对室内蒸发器进行模拟，对比结果表明，模拟结果与实验数据的误差基本能控制在±5%以内，本文提出的蒸发器翅片管换热器的传热模型准确合理。

表1 实验数据与模拟结果比对Table 1 Comparison of experimental data and simulation results

2 结构及运行参数

为了研究二维风速分布不均匀性对蒸发器翅片管换热器的影响，采用本文模型，制冷剂选用R410A 和R22 两种，换热器的结构参数见表2，只研究热泵模式下室外蒸发器侧，运行工况参数见表3。换热管材料默认为铜，翅片为铝。如图2所示，为沿垂直于管长方向的剖面图，沿空气来流方向依次为第一、二、三排，从上到下依次编号；在不均匀风速条件下，为了研究制冷剂流路布置对换热量的影响，设计了三种较为典型的制冷剂流路布置，且都设计为三支路，第一种方式三条支路平行设置，互不影响；第二种方式两条支路交错布置，与另一条支路相互独立，两条支路相互影响；第三种方式三条支路交错布置，相互影响。

表2 换热器几何结构Table 2 Geometry of heat exchanger

表3 蒸发器运行工况Table 3 Operating conditions of evaporator

图2 制冷剂三种不同的流路布置Fig.2 Three different flow path arrangement of refrigerant

对于风速分布的设定，在竖直方向上，参照李权旭[3]等人的风速分布，采用均匀、下三角、上三角和中三角四种，如图3所示；在管长方向上也采用这四种分布方式，下三角、上三角对应于管长方向上的右三角、左三角。两个方向上的四种分布形式相互结合，共16 种二维分布方式，分布方式的表示方法为竖直方向分布形式-管长方向布置方式，如上三角-左三角表示竖直方向采用上三角风速分布方式，同时管长方向采用左三角风速分布方式。不均匀度[4]，即最小风速与最大风速的比值，采用1:5。

图3 换热器的风速分布Fig.3 Wind speed distribution of heat exchanger

3 蒸发器模拟结果和分析

蒸发器模拟结果如图4 和图5所示，为了更方便直观的了解风速分布不均匀对换热量的影响，在绘图时，纵坐标为不同风速分布下的换热量和均匀-均匀下的换热量的差值与均匀-均匀下的换热量的比值，即（Q不同风速分布-Q均匀-均匀）/Q均匀-均匀，为不均匀风速相对于均匀风速所产生的换热量变化率，该值的大小代表换热量衰减或增加程度的大小，比值的正负代表换热量的增加或减少。横坐标采用相同的设置。

通过对图4 和图5 整体趋势的分析，风速的不均匀必然会导致换热器的换热量的变化；在风速分布的两个方向上，竖直方向上的不均匀性对换热量的影响程度要远远大于管长方向上的影响程度；对于第一种和第二种流路布置方式中，竖直方向上，各风速分布下换热量大小基本呈现均匀＞中三角＞上三角或下三角，上三角和下三角分布换热量基本一致；管长方向上，各风速分布换热量大小基本呈现均匀＞左三角或右三角＞中三角，左三角与右三角分布换热量基本一致。三种流路布置方式中，第三个布置方式较其他两个布置方式的曲线更加平缓，换热器在不同风速分布下换热量较稳定；第三种布置方式受上三角风速分布影响最大，而下三角风速分布较中三角风速分布对换热量的影响更小，甚至能够增加换热量。考虑到模拟误差，就R410A 中个别风速分布形式下换热量的变化率相差较大，不具体讨论其规律。

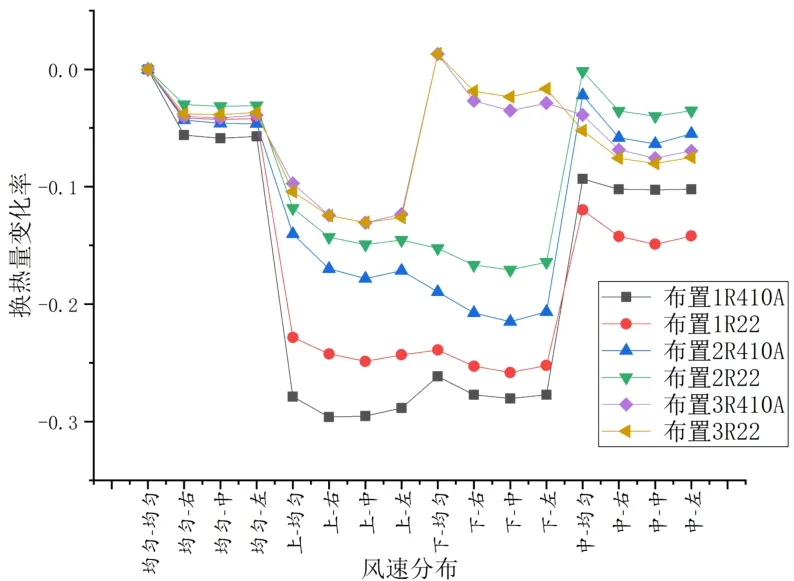
图4 风速分布对蒸发器换热量的影响Fig.4 Influence of wind speed distribution on heat transfer of evaporator

图5、6 和7 显示了R410A 蒸发器三种流路布置时第一排的每根管的每个管段的对流换热系数，每根管划分成了44 个小管段，并沿制冷剂流动方向从1 到44 进行编号。通过对图5、6 和7 的分析，可以发现对流换热系数随制冷剂流动方向增大，在每条支路的最后几根管段，会发现对流换热系数随制冷剂流动方向减小；对流换热系数沿管长方向的变化率基本在10%左右，甚至更低，与竖直方向上的对流换热系数的变化率相比很小，对换热器对流换热系数分布的不均匀性影响较小。再通过对图8的分析，当管内制冷剂干度超过某个值时，这个规律就不再适用，对流路布置2 三条支路进行分析可得每条支路会有3-5 根管不适用于这个规律，其余各管在管长方向上的对流换热系数变化趋势基本可以根据制冷剂流动方向判断。

图5 流路布置1 每根管各管段的对流换热系数Fig.5 Convective heat transfer coefficient of each pipe section in flow path arrangement 1

图6 流路布置2 每根管各管段的对流换热系数Fig.6 Convection heat transfer coefficient of each pipe section in flow path arrangement 2

图7 流路布置3 每根管各管段对流换热系数Fig.7 Flow path arrangement 3 convection heat transfer coefficient of each pipe section

图8 流路布置2 中3 根管对流换热系数与干度之间的关系Fig.8 Relationship between convective heat transfer coefficient and dryness of three root canals in flow path arrangement 2

图9、10 和11 显示了R410A 蒸发器在均匀-均匀风速分布下，各流路布置方式下第一排、第二排和第三排各管的平均对流换热系数，横坐标为1-24，表示该管排从上到下对管依次排序的序号。可以看出，翅片管换热器内共设3 排换热管，在三种不同的制冷剂流路布置中，从每1 排换热管的角度来看，制冷剂与管的对流换热系数随着制冷剂流经各根管子而逐渐变大。在第一种流路布置方式中，三个支路互不影响，第一排和第二排对流换热系数呈三个连续快速减小的规律，第三排对流换热系数基本一致，但较第一排和第二排衰减严重，在竖直方向和深度方向，对流换热系数分布都不均匀；在第二种流路布置方式中，两条支路交错布置且制冷剂流向相反，对流换热系数在前1/3 呈现快速增大的规律，在深度方向分布均匀，后2/3 段在竖直方向上分布较均匀，在深度方向上不均匀；在第三种流路布置方式中，三条支路交错布置且制冷剂流向相同，对流换热系数呈现缓慢增大的规律，在竖直方向和深度方向分布都较均匀。换热器对风速分布不均匀性的敏感程度影响最大的是对流换热系数的不均匀性，而换热器的流路布置直接影响着对流换热系数的不均匀性。

图9 流路布置1 各管排换热系数Fig.9 Heat transfer coefficient of each tube row in flow path arrangement 1

对于第三种流路布置方式，下三角风速分布会增加换热器的换热量，将风速分布与对流换热系数分布一对比，发现两种分布形式基本一致。如果能对对流换热系数分布进行针对性的设计风速分布，能够大大提高换热器的换热量。

图10 流路布置2 各管排换热系数Fig.10 Heat transfer coefficient of each tube row in flow path arrangement 2

图11 流路布置3 各管排换热系数Fig.11 Heat transfer coefficient of each tube row in flow path arrangement 3

4 结论

通过对蒸发器翅片管换热器的模拟和研究，得出以下主要结论：

（1）风速分布不均匀会影响换热器的性能，与均匀风速分布相比，最多能衰减30%的换热量。换热器竖直和管长两个方向的风速分布影响程度不同，竖直方向的影响程度远远大于管长方向的影响程度。

（2）四种风速布置方式对蒸发器换热量的影响程度不同，换热量按照竖直方向比较：均匀＞中三角＞上三角或下三角；换热量按照管长方向比较：均匀＞左三角或右三角＞中三角。

（3）换热器每个微元对流换热系数不同，会根据流路布置方式的不同而变化，其分布的不均匀是风速分布不均匀对换热器性能影响的主要原因。

（4）相对于三种流路布置方式，第三种布置方式，既全交错布置，是对流换热系数分布最均匀，受风速分布不均匀影响最小的布置方式。当风速分布形式与对流换热系数分布形式基本一致时，可以显著增大换热器的换热量。