基于极限平衡法的锚索框格梁支护设计
2022-03-21龙小锋
龙小锋
(甘肃公航旅路业有限公司 兰州 730070)
0 前言
随着我国国民经济与科技水平的发展,高速公路工程的建设飞速发展。有研究资料表明,截至2019年初,我国高速公路总里程突破了14万km,高速公路网日趋完善[1]。高速公路网逐步向多山、深谷地区发展的过程中,面临着地形复杂、不良地质发育、自然灾害频发等问题,公路工程施工不可避免地遇到路堑开挖、高边坡支护等问题,这对项目实施和施工进度带来了极大的挑战[2-3]。山区公路修建过程中,当边坡的高度与坡度较大时,其稳定性是整个边坡工程的控制性因素,高边坡的失稳会导致该区域发生泥石流、崩塌、错落、滑坡等病害,进而导致灾难性的后果[4-6]。
1 公路工程高边坡稳定性分析
1.1 高边坡稳定性影响因素及破坏
由于施工现场环境多变,地质条件复杂,公路工程高边坡施工过程中的稳定性受多种因素影响,结合以往专家学者的研究,可以将边坡稳定性影响因素分为内因和外因两类:内在因素大致包含边坡的内应力、岩体及土体物理力学性能、边坡高度、地质构造、岩体及土体风化程度等;外在因素包括地下水、降雨量、地震活动、风化作用、地表植被等自然因素,也包括爆破、行车振动、路线形式、边坡改造活动、施工方法等人为因素。高边坡稳定性分析中,内在因素对高边坡的设计、施工、防护、失稳等起控制性作用,外部因素则诱导边坡失稳而发生对应的破坏[8-12]。
研究表明,公路工程高边坡的失稳破坏按照其内部的变形与位移发展过程,可分为变形和破坏两个阶段[11]。边坡内部的滑坡体稳定性被破坏发生变形,但尚未形成贯通性破坏面的阶段为变形阶段。变形阶段的破坏模式主要有松动和蠕动两种,松动主要发生在边坡形成之初,滑坡体出现与边坡表面平行的陡倾角张开裂隙,对边坡的坡体产生较强的切割作用,使之不断向边坡的临空面滑移;蠕动是滑坡体受到重力作用后,使之朝着边坡临空面产生缓慢的长期变形。
当松动和蠕变的变形量发展到一定阶段时,坡体中形成贯通性的破坏面,之后以一定的加速度发生位移,则边坡进入破坏阶段。边坡进入破坏阶段后,随着位移量的增加,会导致坡体出现崩塌、滑坡、坍塌、倾倒、错落等破坏形式,引发灾难性的后果。
1.2 极限平衡法的分析过程
基于定量分析的极限平衡法是边坡稳定性分析的传统方法,计算过程相对简便,在实际工程中被广泛应用且获得国内外学者的高度认可。利用极限平衡法求解问题时,将边坡工作过程中受到的所有力简化到同一个平面上,将边坡位置复杂的岩土体简化为不发生变形的刚体[13-14]。
极限平衡法的目标在于求解边坡稳定安全系数[13]。先依据实际工程地质资料确定边坡的结构面,进而综合考虑其受力性能后确定可能发生失稳的潜在滑裂面作为计算岩体下滑的软弱面,其破坏规则遵循摩尔—库伦准则。对潜在滑裂面进行受力分析,对应位置的抗滑力和下滑力的比值即为安全系数。
如图1所示的岩质边坡ABEG,由于滑动面AD的滑动力F和抗滑力Fr的变化,会导致滑动体ABCD沿滑动面产生下滑。
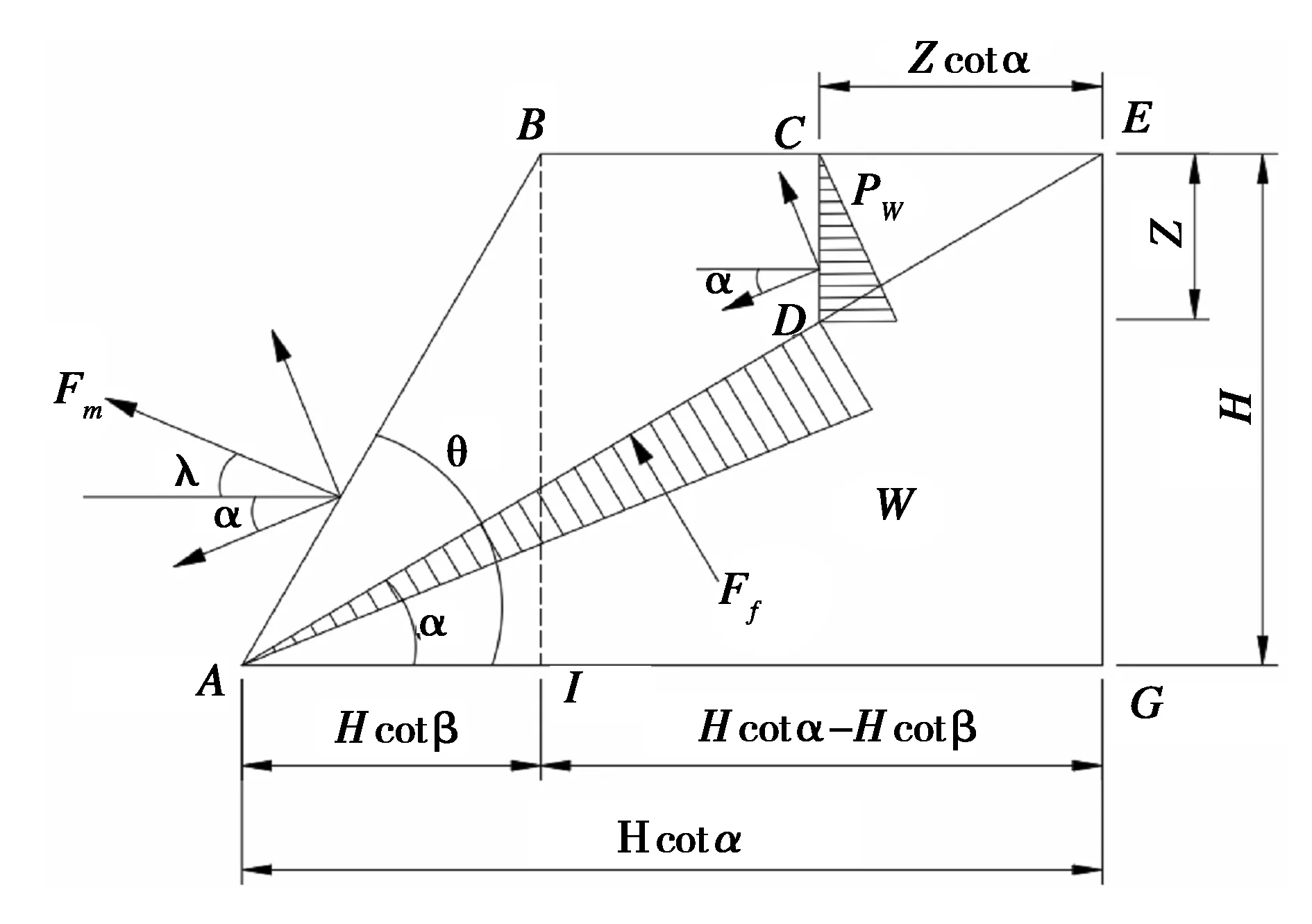
图1 岩质边坡受力分析图
采用极限平衡法分析边坡稳定性时,认为滑裂面与岩体中张拉裂缝的走向与坡面的走向互相平行,在深度为Z的裂缝中对应的充水深度为ZW。由于滑动体对应的岩体本身不会发生渗水,因此水分是沿着垂直方向的张拉裂缝渗透进入滑动体内部,假定水压力沿着裂缝深度呈线性分布。此外,滑裂隙中水的推力PW、滑裂面位置的上浮托力Ff、滑动体的重力W均作用在滑动体的中心,故滑动体只是沿着滑裂面滑动,而不产生转动,且滑裂面的抗剪强度遵循库伦准则τ=c+σtanφ。
1.3 边坡稳定性分析
根据岩质边坡破坏形态的差异,岩质边坡稳定性分析的极限平衡分析方法可分为单平面滑动、多平面滑动、楔形滑动、倾倒和圆弧滑动等破坏。为简化分析过程,以单平面滑动破坏为例,介绍极限平衡法在岩质边坡稳定性分析中的应用。
目前我国地铁建筑工程的施工人员几乎每天都会有变动,流动性比较大,在建筑单位进行进场前的安全教育培训的过程中,加大了工作量,导致安全培训过与形式化,不能将培训效果最大程度的发挥出。当相关工作人员没有安全意识时,就会非常容易出现安全事故。
如图1所示,岩质边坡单平面滑动过程中所受的力包括裂隙中水的推力PW、滑裂面位置的上浮托力Ff、滑动体的重力W、锚固力Fm、黏聚力Fc。依据简单的力学分析可知,滑动体受力为[13]:
(1)
(2)
Fc=cL
(3)
依据库伦定律,岩体ABCD的下滑力F为:
F=[Wsinα+PWcosα-Fmcos(α+λ)]
(4)
阻止滑动体向下滑动的抗滑力Fr为:
Fr=[Wcosα-pWsinα-Ff
+Fmcos(α+λ)]·tanφ+cL
(5)
由(4)式和(5)式可得岩质边坡的安全系数ζ为:
ζ={[Wcosα-pWsinα-Ff
+Fmcos(α+λ)]·tanφ+cL}
÷Wsinα+pWcosα-Fmcos(α+λ)
(6)
式中:γW为水的容重;c为内聚力;L为滑动体的长度;φ为内摩擦角。
基于式(4)~式(6)所述的极限平衡法分析过程,结合实际工程的地质资料,可以初步得到对应边坡的安全系数,判断其发生滑动的可能性,并为后续支护方式及参数设计、施工方法选择等提供依据。
2 基于极限平衡法的锚索框格梁设计
2.1 工程概况
该项目是我国西南某地干线公路网的组成路段,主线为双线4车道高速公路,设计速度80km/h,线路全长235.966km。现场勘探资料表明,上述三段均处于构造剥蚀中、低山地貌区,地表水为当地河流,与线路中心距离约150m,无其他明显地表水体,路线区地震基本烈度为Ⅶ度。
根据现场资料,项目全线共有3处风险等级为Ⅲ级的高度风险边坡工程。其中里程K143+490.00~810.00段为岩质边坡,全长320m,坡高68.6m,坡高1~5级分别为10 m、10 m、10 m、10 m、28.65m。设计为五级边坡,每级边坡设置2m平台,设计坡率为1∶1,采用锚索框格梁防护。K143+720典型断面如图2所示。
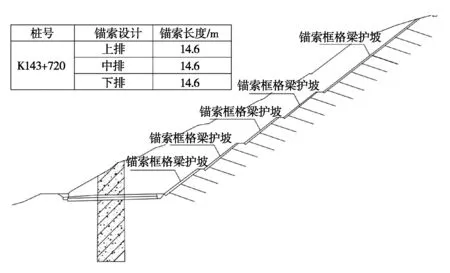
图2 里程K143+720典型断面图
该段地质岩土自上而下分别为粉质黏土、强风化砂岩、中风化砂岩。地质勘探资料显示,该里程范围内坡体平均内聚力为10.5kPa,平均内摩擦角φ为30°,自然坡度为40°,孔隙水及裂隙水的平均埋深为10.5m,岩土体天然重度取13.75kN/m3。
2.2 锚索的索力设计
依据(6)式所述的边坡稳定性分析,当边坡的抗滑力Fr大于滑坡体的极限滑动力F时,滑动体处于稳定状态。锚索框格梁通过将预应力锚索稳固地锚固于边坡坡体内部的稳定持力层,依靠坡体自身强度和可靠的自稳能力使体系产生足够的抗滑力[13]。以滑动体产生滑动的临界状态为限值,设计锚索索力的临界值。由(6)式可知,当安全系数ζ=1时,滑动体处于临界状态。因此,可得锚索的临界索力为:
Fm=[W(sinα-tanφ·cosα)
+pW(cosα+pWtanφ·sinα)
+Fftanφ-cL]/cos(α+λ)·(tanφ+1)
(7)
将本项目对应的地质数据代入(7)式,得到临界索力为805.6kN,低于实际工程中采取的索力1040kN,锚索最大极限张拉力为索力的一半。
2.3 锚索锚固角设计
依据(6)式所述的边坡稳定性分析,边坡的抗滑力Fr大于滑坡体的极限滑动力F时,滑动体处于稳定状态。锚索框格梁通过将预应力锚索稳固地锚固于边坡坡体内部的稳定持力层,依靠坡体自身强度和可靠的自稳能力使体系产生足够的抗滑力[15]。锚索的受力分析如图3所示。
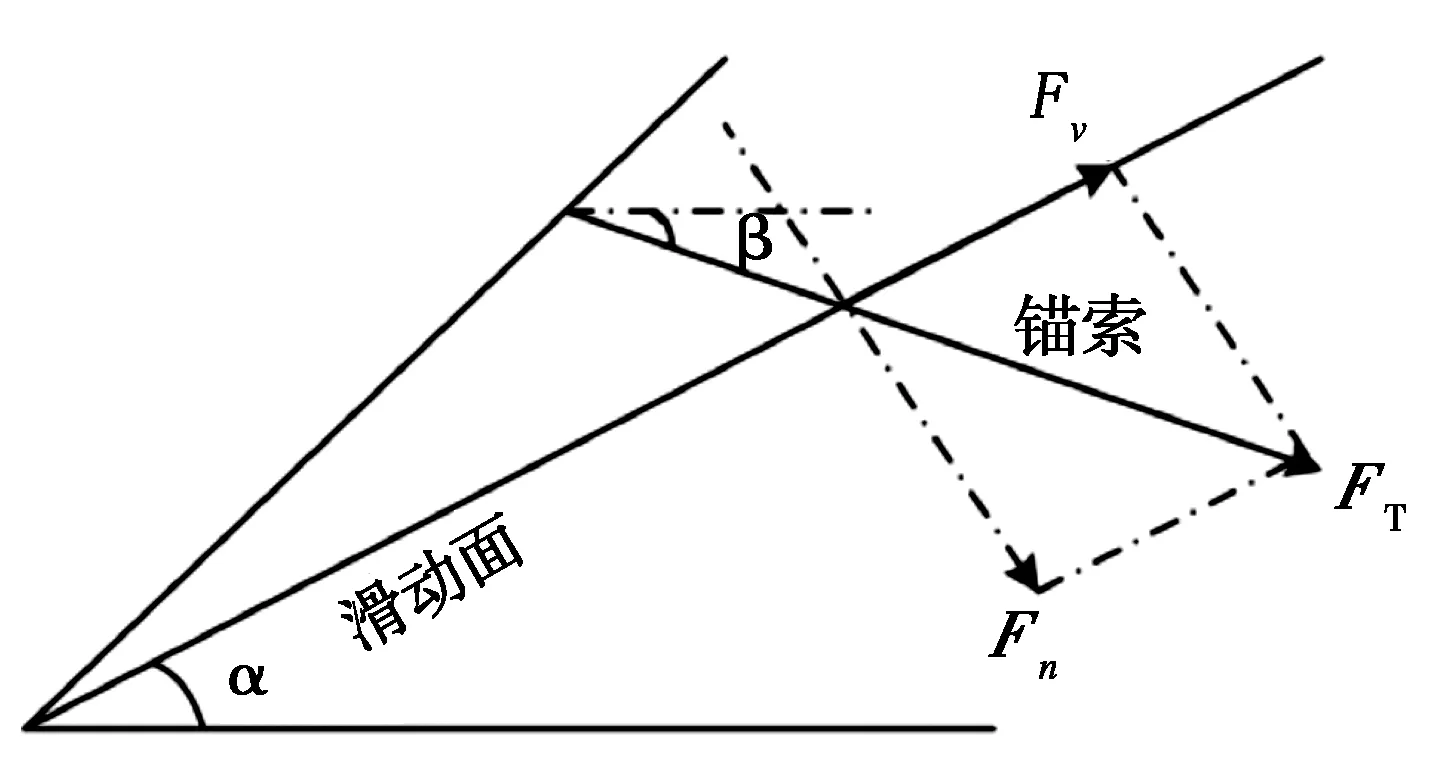
图3 锚索受力分析图
由图3可知,锚索通过在平行垂直于滑动面两个方向上产生锚固力,使框格梁体系产生足够的抗滑力。锚固角不同,所产生的抗滑力大小会产生较大的差异。考虑施工成本的基础上,为使锚索达到最佳的受力状态,选用最大抗滑力对应的锚固角为最优锚固角[15]。如图3所示,根据力学平衡原理,可得锚索持力后提供的最大总抗滑力为:
Fr=Fv+Fn
=FT[sin(α+β)tanφ+cos(α+β)]
(8)
式中:FT为锚索极限承载力;Fn、Fv分别为Fr的水平分量和垂直分量;β为锚固角。
结合(4)~(6)式,依据设计所提供的锚索极限承载力及实地勘探所得的地质资料,计算得锚固角为25°。实际工程中取锚固角为30°,以保证锚固性能,偏安全地设计锚索工作性能。
2.4 锚固段长度、锚索长度及间距
实际工程中锚索框格梁的锚索锚固段长度、锚索材料、锚索长度及锚索间距等参数,在满足锚固力设计要求的基础上符合构造要求。锚索的构造需综合考虑经济成本和加固效果。锚索长度包括锚固段、自由段和锁定头。锚索的总埋深应大于潜在滑裂面的深度,岩层锚索的锚固长度应大于3m。
此外,预应力锚索的耐久性是制约其使用寿命的重要因素之一,对支护效果起控制性作用,需对锚索采取防腐措施,如涂覆防腐涂层、外套防腐塑料管等。设置锚索的间距过小时会引发群锚效应,降低单根锚索的工作效率,显著增加施工成本。因此,依据规范规定,本项目锚索框格梁锚索的各个参数取值如表1所示。
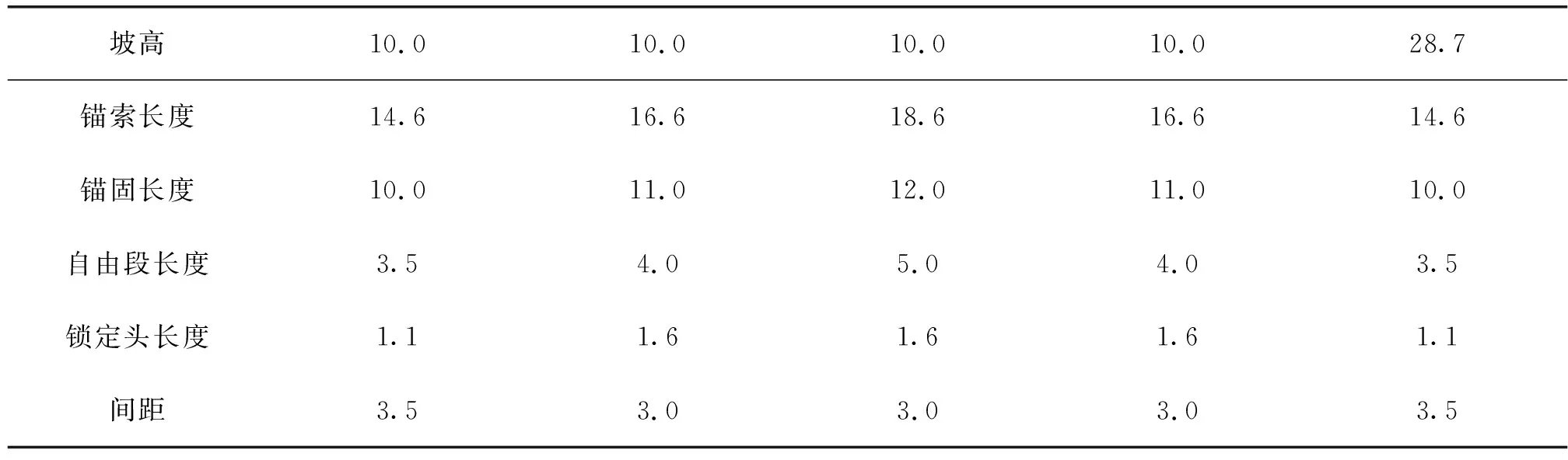
表1 锚索框格梁锚索的参数取值(单位:m)
为保证锚固效果,本项目锚索由四根φ15.2mm、强度为1860MPa的高强度低松弛无黏结的钢绞线组成。为保证防腐效果,对钢绞线进行除锈处理,涂刷强力防腐涂料。在自由段涂防护油并套上厚度为1mm的原生塑料管。自由段与锚固段相接处采用止水效果较好的黏胶带缠封。与实际工程的保守型设计对比后发现,采用极限平衡法设计的锚索参数符合施工要求。
3 结语
锚索框格梁通过将预应力锚索稳固地锚固于边坡坡体内部的稳定持力层,依靠坡体自身强度与自稳能力使体系产生足够的抗滑力,锚索工作性能是影响其支护和加固效果的主要因素之一。采用极限平衡法求解边坡稳定系数的思路,基于岩质边坡单平面滑动破坏的受力分析,反算得到了锚索的临界索力;依据对锚索的受力分析,结合实际工程的地质参数设计了锚索索力、锚固角、锚固段长度、锚索长度及间距等参数。将计算得到的锚索设计值与实际工程采取的锚索工作参数对比表明,采用极限平衡法设计的锚索工作参数能满足施工要求。
