离散型整数规划的城市公共自行车系统选址模型
2022-03-21邵卿
邵 卿
(湖南铁路科技职业技术学院,湖南 株洲 412000)
目前,对公共自行车共享系统布局的研究为系统运营和租赁点的位置确定,主要集中在布局原则、特征分析和规模预测上。方云飞等[1]以公交站点为中心,建立以最大化满足用户需求量为优化目标的公共自行车选址的非线性优化模型。姚学儒等[2]将运营时间划分为多个时间段,以最小化未满足需求为目标函数,构建规划模型,确定公共自行车系统租赁点位置、桩位配备数量。有关定量模型的研究较少,未体现公共自行系统微观动态具体过程。文章分析用户出行需求和公共自行车系统供给,构建基于离散型整数规划的公共自行车选址模型,为公共自行车系统发展提供思路。
1 问题描述
城市公共自行车系统一般性网络结构能够为周围居民提供自行车共享设施,解决“最后一公里”问题。
公共自行车系统网络结构如图1所示。
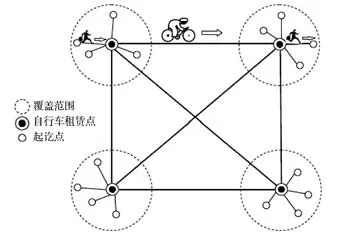
图1 公共自行车系统网络结构
某规划区域内具有R个自行车需求点、M个候选自行车租赁点,选择部分候选租赁点进行建设,在这些建设的租赁点分配一定数量的自行车和停车桩以满足一天内各个时段居民的出行需求。保证任一时段居民在其步行范围内的租赁点均能够借车和还车,使规划区域内居民总出行时间最短。
居民出行时间包括起始需求点到租赁点的时间、租赁点到租赁点的时间和租赁点到目的需求点的时间。将7~19点划分为6个时段进行研究。
2 模型构建
2.1 模型假设
出行者了解步行范围内哪些租赁点可以提供自行车和空的停车桩;各个需求点的出行是规划区域内的出行,不考虑区域外的出行对各个需求点产生的影响;各个需求点之间的自行车出行量已知;每个租赁点的固定建设成本相同;全天自行车出行量集中在7~19点,其余时间自行车的借还需求很小,忽略不计。
2.2 参数和变量
(1)决策变量。yj——候选点j建设租赁点,yj=1,否则yj=0;ParkPile(j)——候选租赁点j分配的停车桩数;Bike(j)——候选租赁点j分配的自行车数。
(2)其他变量指可以由决策变量计算得到的非常量。Biji′(t)——第t个时段需求点i到需求点i'的出行者在候选租赁点j的借车数;Rij′i′(t)——第t个时段需求点i到需求点i'的出行者在候选租赁点j'的还车数;Eijj′i′(t)——第t个时段需求点i到需求点i'的出行者在候选租赁点j所借的自行车中还到候选租赁点j'的自行车数;Xj(t)——第t个时段初第j个候选租赁点空闲的停车桩数;Pj(t)——第t个时段第j个候选租赁点可以提供的自行车数;Qj(t)——第t个时段第j个候选租赁点可以提供的空闲的停车桩数。
(3)常量。dij——第i个需求点到第j个租赁点的距离;djj'——第j个租赁点到第j'个租赁点的距离;-y——最少需要建设的自行车租赁点数目;-y——最多能够建设的自行车租赁点数目;d0——出行者步行距离上限;aij——第i个需求点可以由第j个候选租赁点服务时,aij=1,否则aij=0;M——足够大的正整数;g——每个自行车租赁点的固定建设成本;f1——每辆自行车的购买成本;f2——每个停车桩的安装成本;IG——规划区域总投资额;Oi(t)——第t个时段第i个需求点的自行车出行发生量;Di(t)——第t个时段第i个需求点的自行车出行吸引量;Wii′(t)——第t个时段需求点i到需求点i'的自行车出行量;α——每个自行车租赁点最少需要分配的自行车数;u1——出行者的步行速度;u2——出行者的骑车速度;dmin——自行车租赁点间的最小距离;ω——自行车服务站点服务能力下限;η1——停车桩数多于自行车数的下限,取0.1;η2——停车桩数多于自行车数的上限,取0.3。
2.3 模型构建
每个时段初租赁点拥有的自行车数为上一时段末剩余的自行车数,且与本时段该租赁点服务范围内需求点的自行车出行发生量和出行吸引量有关。为使规划区域内所有出行者总出行时间最小的目标,选择待建租赁点及分配各点自行车数和停车桩数。在规划区域内,设I(i∈I)为需求点的集合,J(j∈J)为候选租赁点的集合,J1为建设的租赁点的集合,T(t∈T)为各个时段的集合。建立自行车租赁点选址模型:
目标函数包括起始需求点到租赁点的时间、租赁点到租赁点的时间和租赁点到目的需求点的时间。
约束规划区域内自行车租赁点的建设数目。
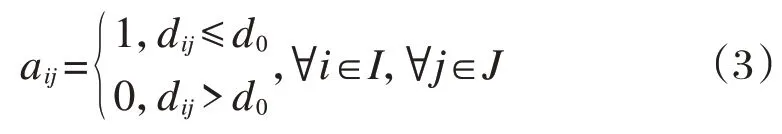
定义0-1矩阵,保证服务站点只为最大服务范围内的需求点提供服务。
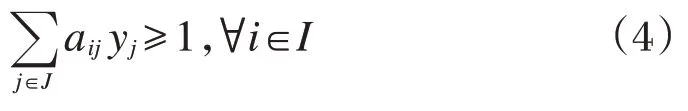
每一个需求点至少有一个服务站点。
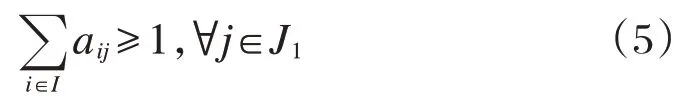
每个已决定建设的租赁点,保证至少有一个需求点作为其服务对象。
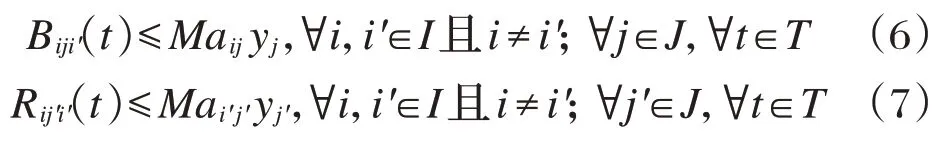
自行车出行者的借、还车需求只能够在候选租赁点进行,且租赁点需在步行距离范围内。
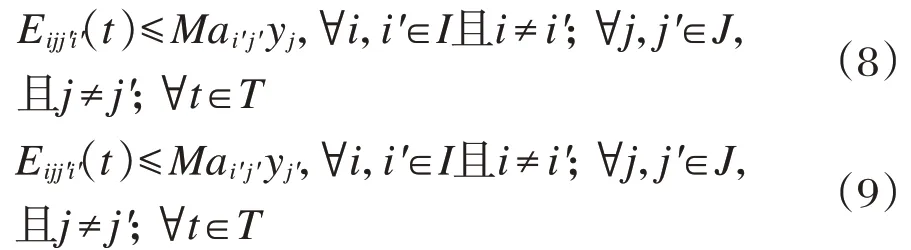
位于起始需求点和目的需求点步行距离范围内且建设在租赁点间才有自行车出行。
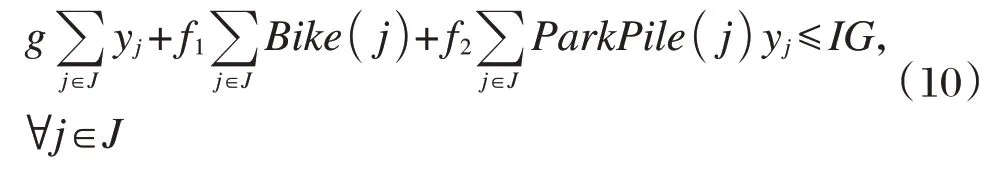
整个规划区域内,自行车的购买成本、停车桩的安装成本和租赁点的固定建设成本应不超过总投资额。
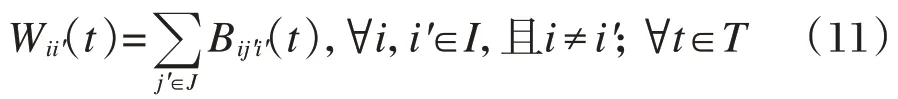
起始需求点到目的需求点的自行车出行量等于起始需求点的出行者在各个租赁点的借车数之和。且j≠j′;∀t∈T
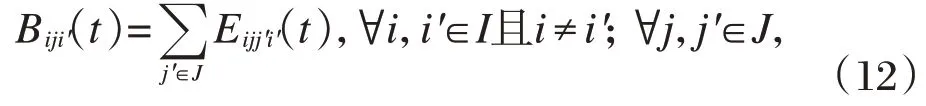
起始需求点到目的需求点的自行车出行量等于到目的需求点的出行者在各个租赁点的还车数之和。
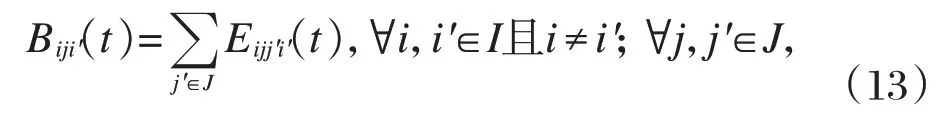
且j≠j′;∀t∈T
起始需求点到目的需求点在一个租赁点的借车数等于该租赁点到其他租赁点的自行车数之和。
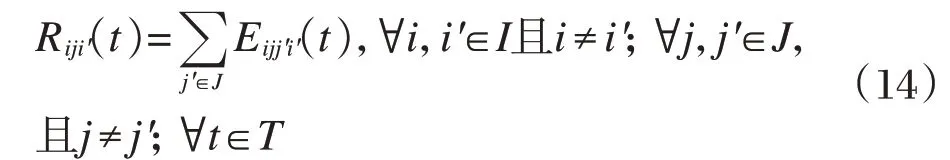
起始需求点到目的需求点在一个租赁点的还车数等于其他租赁点到该租赁点的自行车数之和。
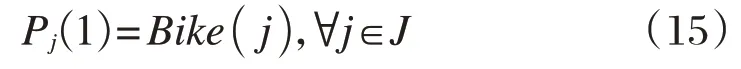
定义每一天开始时刻每个租赁点均有车可用。
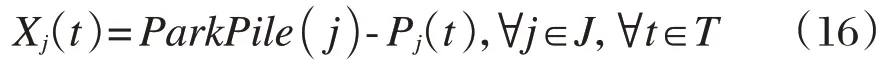
定义每个时段初每个租赁点空闲的停车桩数。
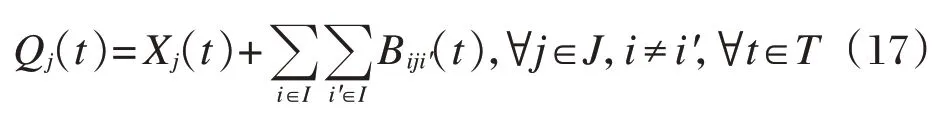
定义每个时段末每个租赁点剩余的空闲停车桩数。
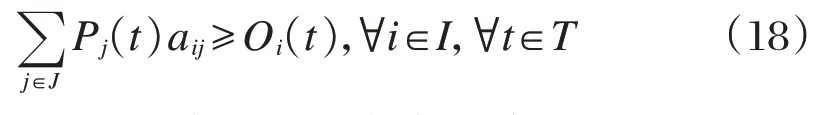
任一时段可以为某需求点提供服务的租赁点,可以提供的自行车数不小于该需求点总的借车需求。
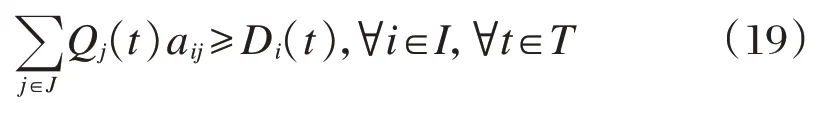
任一时段需求点范围内的租赁点得满足到该需求点总的还车需求。
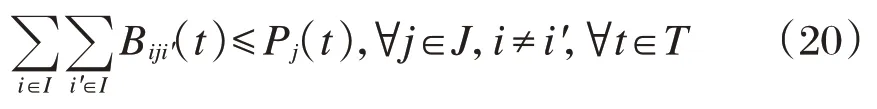
任一时段各个需求点在某个租赁点的借车数之和应不大于该租赁点可以提供租赁的自行车数。
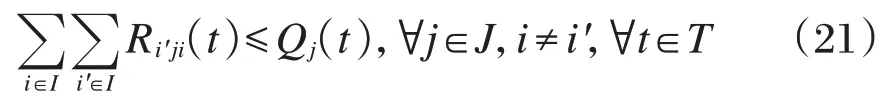
任一时段到各个需求点在某个租赁点的还车数之和应不大于该租赁点可以提供还车的空闲停车桩数。

每个建设的租赁点最少需要分配的自行车数。
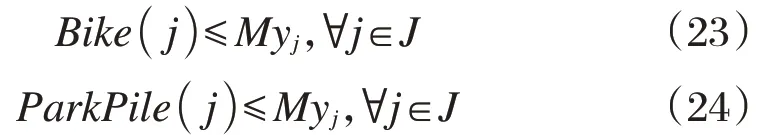
建设的租赁点才分配自行车和停车桩。

候选租赁点是否建设变量的0-1约束。
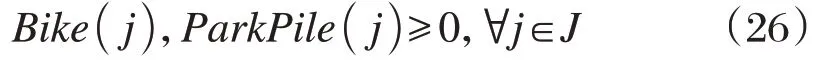
部分决策变量的非负约束。
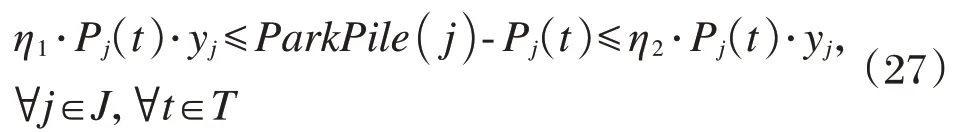
限制各租赁点的停车桩数大于其所能拥有的自行车数,且其差值处于一个合适的范围。
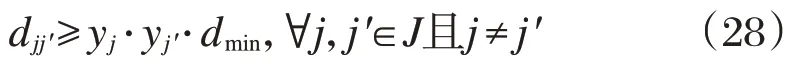
约束两个租赁点间距不能过小。
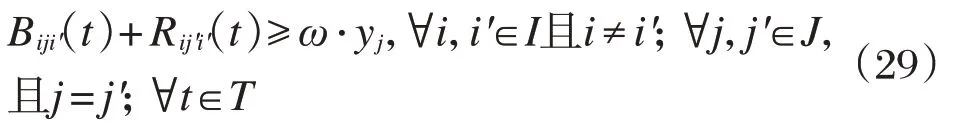
保证待建站点的服务水平,服务发生总量未超过某一定值时,不允许被设置。
3 算例分析
3.1 算例简介
拟在某规划区域建设公共自行车租赁系统,投资总额为360万元。确定10个自行车出行需求点,依据需求点确定20个候选租赁点。从20个租赁点中选择部分租赁点建设,分配相应数量的自行车和停车桩,满足一天内各个时段居民的出行需求。
需求点和租赁点分布如图2所示。

图2 需求点和租赁点分布
3.2 算例求解
(1)相关常量取值。C为400 m、g为50 000元、f1为300元、u1为1.4 m/s、M为100 000、α为15辆、f2为2 000元、u2为5 m/s。
(2)根据租赁点与需求点之间的距离以及租赁点的服务半径C,得每个需求点对应的候选租赁点。
(3)通过软件编程求解,规划区域内居民最短的总出行时间为3 968 294 s,应建设的租赁点为编号2、3、4、7、8、9、11、12、14、15、16、20,共12个。
租赁点分配的自行车数和停车桩数如表1所示。
依据选址方案及租赁点和需求点之间的距离表可得到每个建设的租赁点应服务的需求点。
租赁点服务需求点如图3所示。
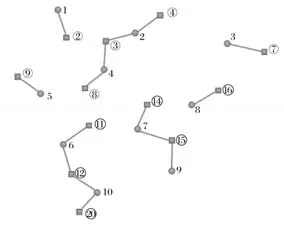
图3 租赁点服务需求点
4 结语
文章从用户出行需求和公共自行车系统供给出发,建立基于离散型整数规划的公共自行车选址模型。后续研究中,应对出行需求进行更准确的统计及预测。
