光伏电站复合储能电压波动抑制双层优化控制方法
2022-03-21孙阔张雪菲迟福建李桂鑫罗涛张梁
孙阔,张雪菲,迟福建,李桂鑫,罗涛,张梁,3
(1.国网天津市电力公司,天津 300010;2.国网天津市电力公司经济技术研究院,天津 300017;3.天津大学,天津 300072)
0 引言
近年来,随着储能设备的发展,大规模储能系统得到了广泛的应用。在电力系统中,储能设施可灵活地接入系统,且储能设备的投入几乎不受地理位置的限制。储能装置可安装在光伏电站,实现储能装置和光伏发电设备的协调优化控制,达到稳定控制并网电压的效果[1],[2]。当系统中光伏出力较大,且负荷无法全部消纳光伏电站输出的电能时,可通过储能系统吸收部分电能,合理控制储能系统中蓄电池及超级电容的充放电时间,实现系统的电压波动抑制。
国内外专家学者针对可再生能源出力波动性的抑制问题进行了大量研究。文献[3]分析了分布式电源出力情况,根据变流器的控制特性,采用一种基于阻尼分配的无源控制策略,提高超级电容电池储能系统的动态响应。文献[4]针对超级电容储能系统提出了一种滑模控制方法,可在一定程度上提高超级电容的充电效率,提高了设备的使用寿命,使得电池储能系统在应对暂态情况下具有更快的响应速度,增强了控制系统的鲁棒性。文献[5],[6]采用模糊控制算法对超级电容电池储能系统进行控制,利用该控制策略在保证直流母线电压稳定的前提下,提高电池储能系统的功率输出能力。文献[7]通过重新设计电池储能部分,协调控制电池储能与超级电容,在一定程度上缓解了独立光伏电站出力波动对电池组的储能压力。文献[8]分析了独立微电网系统和并网微电网系统在储能方面所面临的挑战,并在储能技术的研究和实践上提供必要的理论指导。为了保证电力系统在供能安全可靠的前提下,使得整个系统的碳排放量最低,文献[9]~[12]研究了基于碳交易的含大规模光伏发电系统复合储能优化调度方法。以上研究大多是研究储能系统的优化控制算法,但是对于有关复合储能中超级电容与蓄电池之间的协调优化控制,抑制光伏电站的出力波动,提高系统电压稳定性的研究较少。
本文为解决光伏电站出力不确定性对并网点造成的电压波动问题,通过分析光伏电站并网点电压波动安全范围,结合复合储能系统中蓄电池及超级电容充放能特性,建立了复合储能间协调优化的控制模型;采用双层优化控制策略,实现光伏电站输出的稳定性;在不同频率信号下,调度不同的储能设备进行充放电;采用改进粒子群优化控制算法,实现光伏电站与复合储能一体化的电压优化控制。
1 光伏混合储能系统模型
1.1 混合储能系统拓扑模型
随着光伏发电并网容量的不断增加,电网受到的不确定性冲击也随之增加。为应对和解决光伏电站的出力波动性及不确定性对电网电压造成的冲击问题,根据图1所示的光伏电站复合储能系统结构,进行光伏电站电压控制。
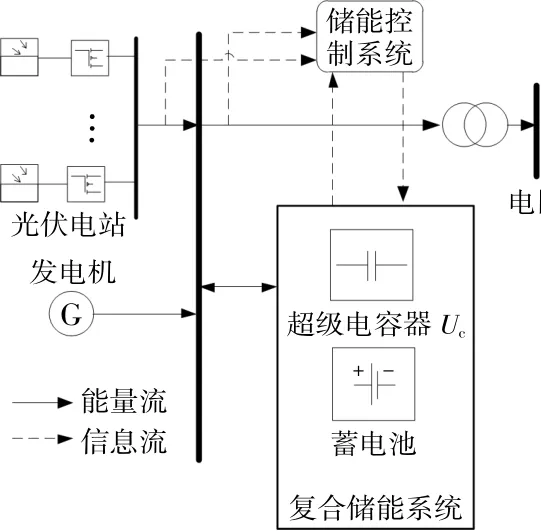
图1 光伏电站复合储能结构示意图Fig.1 Schematic diagram of composite energy storage structure of photovoltaic power station
当蓄电池储能装置电源突然变化时,超级电容进行吸收缓冲或提供瞬态电流,为系统电压稳定提供必要调节作用。超级电容与蓄电池协调控制过程中,控制系统将动态能量交换定向到超级电容储能系统,在外部环境发生变化时保证蓄电池存储的电能充放平衡。
1.2 双层优化控制策略
针对复合储能系统中蓄电池及超级电容的储能差异、储能单元SOC过高或过低导致储能系统充放能特性不稳定等问题,本文提出计及储能调节电压和SOC恢复的多储能系统调压双层优化策略。优化控制框架包括储能系统电压调节优化层和储能单元SOC优化层(图2)。
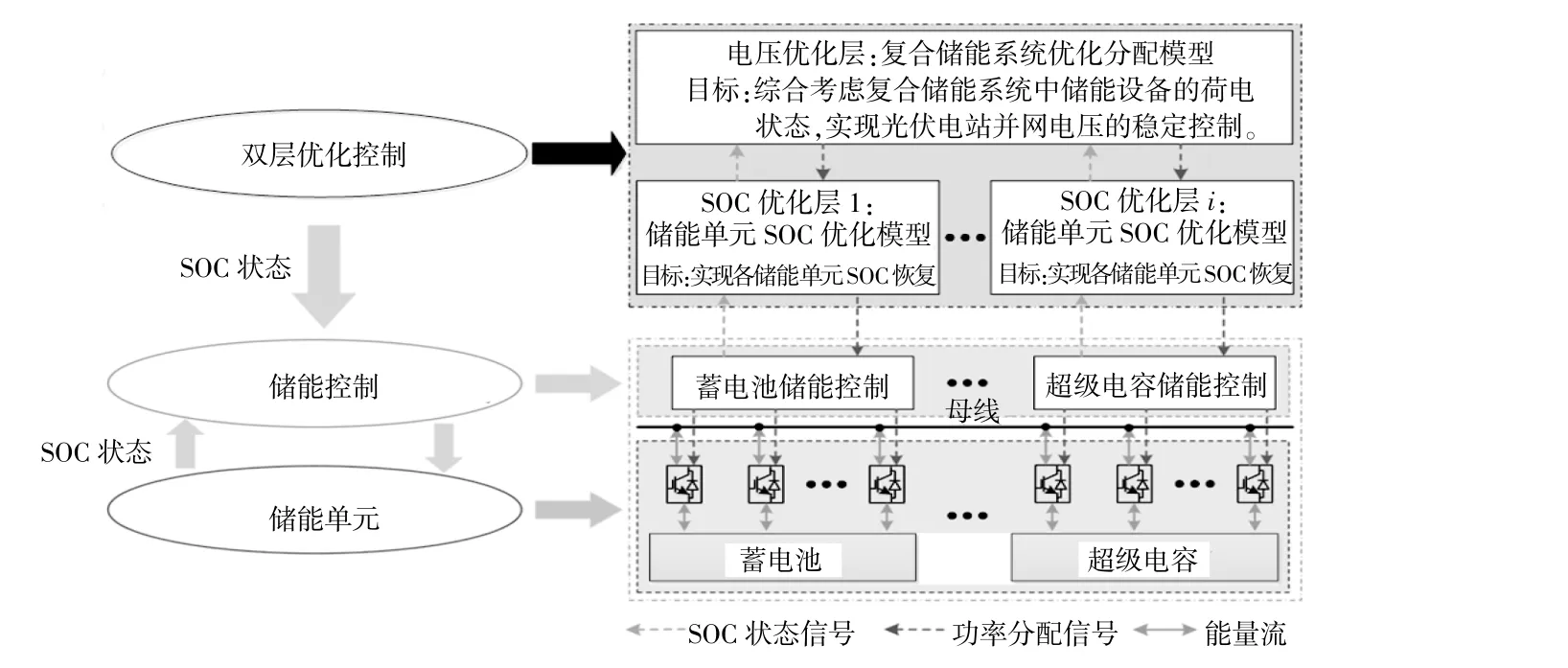
图2 双层优化控制策略Fig.2 Two-layer optimization control chart
系统电压控制优化层采用储能电站功率优化分配模型。综合考虑各储能单元的电压调节和剩余的充放能容量,在复合储能间分配蓄电池及超级电容的储能容量。SOC优化层采用储能单元SOC优化模型。将电压调节优化层优化结果在每个储能电站内部的各储能单元之间进行再分配,以储能单元SOC状态最佳为目标,实现储能单元SOC的恢复。
本文所提的双层优化控制策略可实现电压的分级控制,既能抑制光伏电站并网功率波动,又能对储能单元SOC进行合理优化,保证复合储能系统在任何情况下电压控制的可靠性。
针对光伏电站出力波动性,通过超级电容的快充快放特性,最大限度地减少动态功率交换,缓解电池存储压力。使用低通滤波器将净功率需求分解为高频和低频分量,在控制系统中,超级电容主动为高频电源进行能量交换,而低频电源将由蓄电池供电。为了实现混合储能协调控制,采用一种超级电容优先蓄电池后补的混合储能系统协调控制策略。当系统电压突然升高时,蓄电池组和超级电容共同维持新能源直流侧电压稳定。该控制策略可分为共同充电状态、超级电容充电状态、超级电容放电状态、共同放电状态。复合储能协调控制如图3所示。
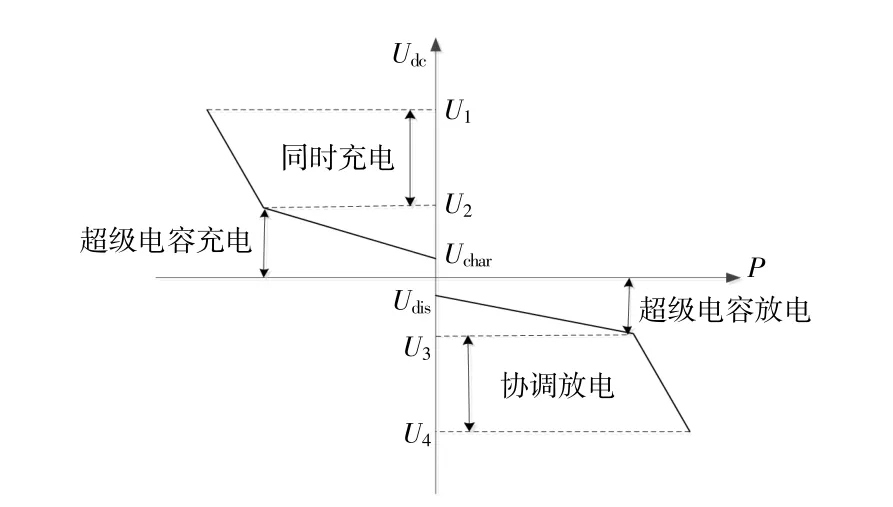
图3 复合储能协调控制示意图Fig.3 Schematic diagram of the coordinated control of composite energy storage
1.3 复合储能能量协调模型
为确定在不同功率波动下复合储能系统中蓄电池和超级电容的储能容量分配,应充分考虑储能设备能量值与初始能量。蓄电池和超级电容的能量计算式为[13],[14]
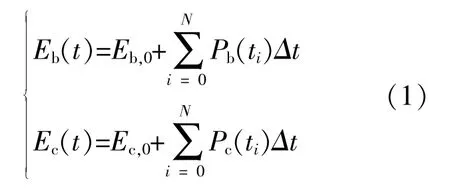
式中:Eb,0,Ec,0分别为蓄电池和超级电容器在初始时刻的电能存储量;Eb(t),Ec(t)分别为蓄电池和超级电容器在t时刻的能量值;i为时间节点;Pb(ti)为系统中蓄电池的充放电额定功率;Pc(ti)为系统中超级电容充放电额定功率;N为从初始时刻到t时刻的采样点数。
当复合储能系统长时间处于充电或放电状态时,在一定程度上影响其使用寿命。通过设定储能系统运行时荷电状态的上下限,使储能系统荷电状态始终处于一定范围,减少其寿命损耗,使系统经济性更佳。蓄电池和超级电容器的额定容量由下式表示:

最大充放电功率为储能实时功率序列的无穷范数。
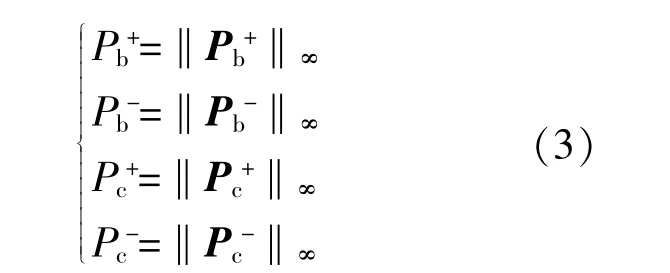
式中:Pb+,Pb-分别为蓄电池的最大充、放电功率;Pc+,Pc-分别为超级电容的最大充、放电功率;Pb+,Pb-分别为蓄电池的充电功率集合、放电功率集合;Pc+,Pc-分别为超级电容的充电功率集合、放电功率集合。
考虑到储能元件充放电特性的不确定性及充放电效率的影响,复合储能系统投入蓄电池和超级电容的功率及容量为

2 光伏并网点电压波动优化控制模型
2.1 目标函数
复合储能系统的主要优化目标是尽量减少由于光伏电站接入对电网带来的电压波动,同时能够在一定程度上降低系统网损,提升电网电压稳定性水平。复合储能系统的目标函数为
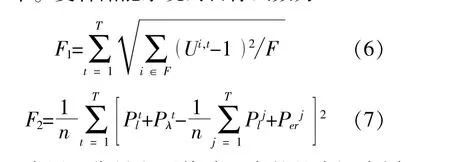
式中:F1为用于衡量电压偏移程度的整个调度周期内配电网各节点电压的标准差;F2为用于衡量负荷波动大小的整个调度周期内配电网负荷曲线方差;T为系统调度周期;F为配电网节点总数;Ui,t为t时刻i节点处电压标幺值;Plt为t时段系统负荷功率;Pλt为t时段储能装置的输出功率。
对多目标进行归一化处理:
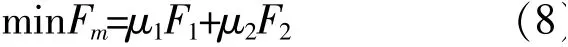
式中:μ1,μ2为对应目标的权重系数。
2.2 约束条件
为保证复合储能系统的安全可靠运行,保证母线潮流的稳定性,其复合储能系统潮流约束为
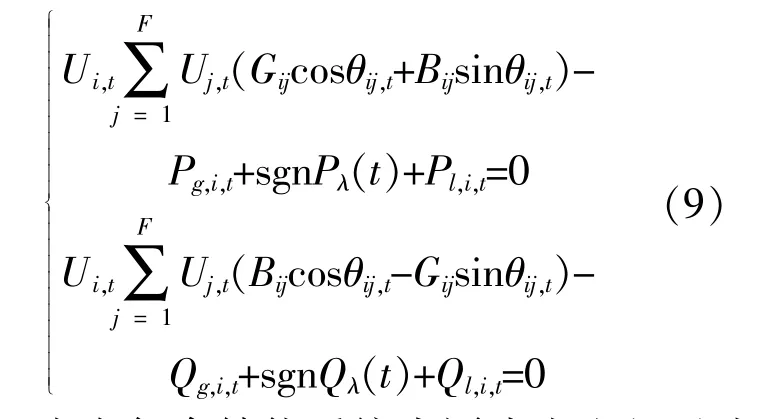
式中:Pg,i,t为在复合储能系统中同步发电机及光伏电站的总输出有功功率;Pλ(t)为储能的有功交换功率;Pl,i,t为系统中负荷有功功率;Qg,i,t为在复合储能系统中同步发电机和光伏电站的总输出无功功率;Qλ(t)为储能的无功交换功率;Ql,i,t为系统中负荷无功功率;sgn为符号函数,当储能装置充能时取1,当储能装置放电时取-1;Ui,t,Uj,t分别为在t时段i节点及j节点处的节点电压;Gij为i节点与j节点线路之间的电导;Bij为i节点与j节点线路之间的电纳;θi,j,t为t时段i节点与j节点处的电压相角差。
储能设备约束:

式中:Pλ,in(t),Pλ,out(t)分别为储能装置λ在t时段的充、放能功率;Pλ,in,max,Pλ,out,max分别为储能装置λ充、放能功率的上限;Xλ(t),Yλ(t)分别为储能装置λ在t时段的状态,取值为1时表示储能装置处于充能状态,取值为0时表示储能装置处于放能状态;Eλ(t)为装置λ在t时段的储能容量;Eλ,max,Eλ,min分别为装置λ的储能容量上限和下限值。
考虑储能运行周期性,各周期初始条件相同。
安全运行约束:
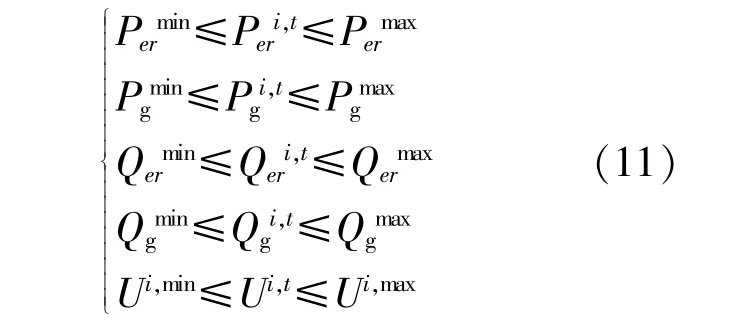
式中:Permax,Permin分别为储能装置与母线的有功交换功率上、下限;Qermax,Qermin分别为储能装置与母线无功交换功率上、下限;Pgmax,Pgmin分别为储能系统中发电机出力的有功功率上、下限;Qgmax,Qgmin分别为储能系统中发电机出力的无功功率上、下限;Ui,max,Ui,min分别为在节点i处的电压上、下限。
3 改进量子粒子群算法
为得到并网点电压波动最小的最优结果,采用量子粒子群算法(Quantum Particle Swarm Optimization,QPSO)对目标函数进行求解计算。利用QPSO求解高难度的复杂问题时,可能会遇到寻优能力差、早熟收敛的问题。本文采用一种改进QPSO求解模型,应对含有多个决策变量、多个约束的高维非线性所造成的动态波动问题。改进QPSO算法采用量子位的概率幅作为粒子的当前位置编码,将归一化后的目标函数表示为
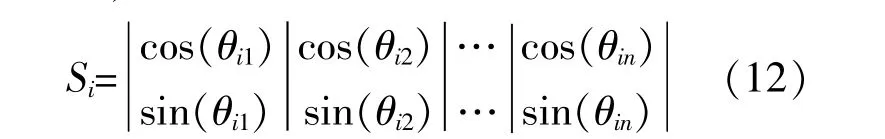
式中:Si为第i个粒子位置,即在不同时刻下电压波动最小的最优解;n为目标函数中的子目标个数,即各节点电压的标准差以及配电网负荷曲线方差,其中余弦位置Sic和正弦位置Sis分别对应着量子态0和1的概率幅;cos(θin),sin(θin)分别为第i个粒子中的第n个目标对应的余弦和正弦位置。
同一个粒子可表示两种状态,对应多个解空间中的位置。加快算法的收敛速度,提高算法的搜索精度,快速得到所有粒子个体最优位置,从而得到目标函数的最优解。
式(13)将粒子两个单位空间位置转变为电压波动最小目标函数的解空间正弦位置Xisj和余弦位置Xicj。
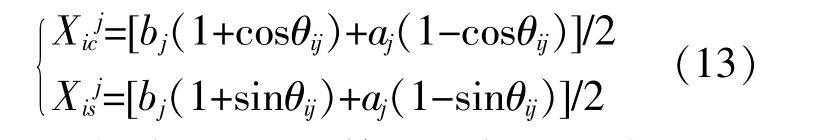
式中:aj,bj分别为量子的第j个位置,即优化问题的第j个变量的最大值与最小值。
(1)混沌搜索提高初始种群质量
混沌搜索具有良好的随机性、遍历性和对于初始条件的敏感性。将其应用于种群初始化之中,能够提高初始种群多样性,有效提高算法的收敛能力。
利用如式(14)所示的Logisitic映射产生混沌序列,进行混沌搜索。

式中:i为粒子编号;u为混沌状态的程度,u∊[0,4],为使系统序列完全混沌无重复,取u=4。
在随机生成一组共n个初始单位空间序列后,迭代m次后转换至弧度空间,即可生成种群总数为m,维度为n的初始种群。
(2)位置更新方式改进
利用量子行为位置更新方程式对更优位置进行更新,然后返回θi值,从而构成更新的粒子i的正弦位置和余弦位置,进而构成如式(15)所示的粒子i的当前位置编码。
位置更新方程如式(15)~(18)所示。
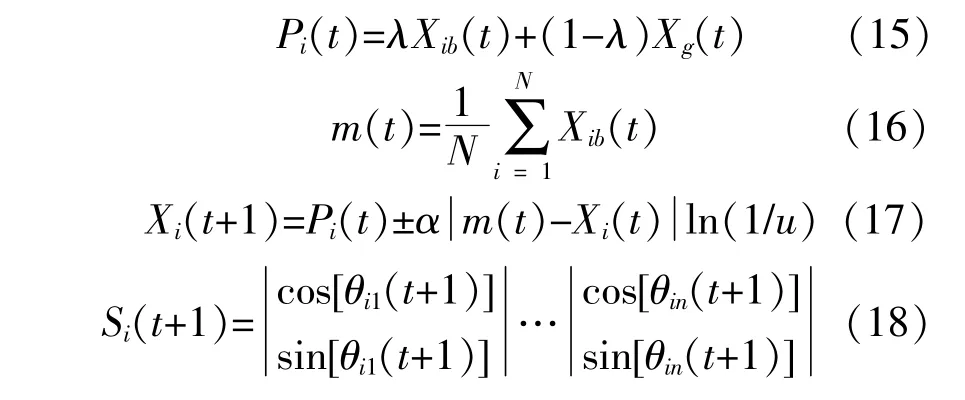
式中:Xib,Xg分别为粒子个体最优位置、种群全局最优位置;λ和u均为[0,1]的随机数;N为种群的大小;m为种群中所有粒子个体最优位置的平均值;α为收缩-扩张因子,通常线性减小。
优化计算流程如图4所示。
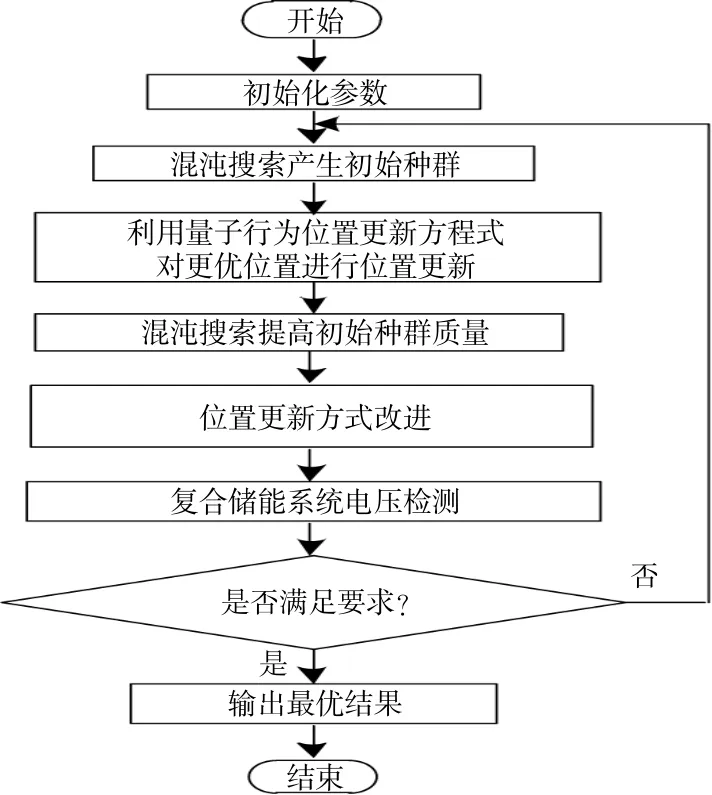
图4 优化计算流程图Fig.4 Optimization calculation flow chart
4 仿真验证
为了验证本文所提出的光伏电站复合储能电压波动抑制双层优化控制方法的有效性,以实际光伏电站与复合储能装置为例进行仿真验证。图5为复合储能系统仿真图。复合储能系统中光伏电站容量以及储能装置容量相关参数如表1所示。
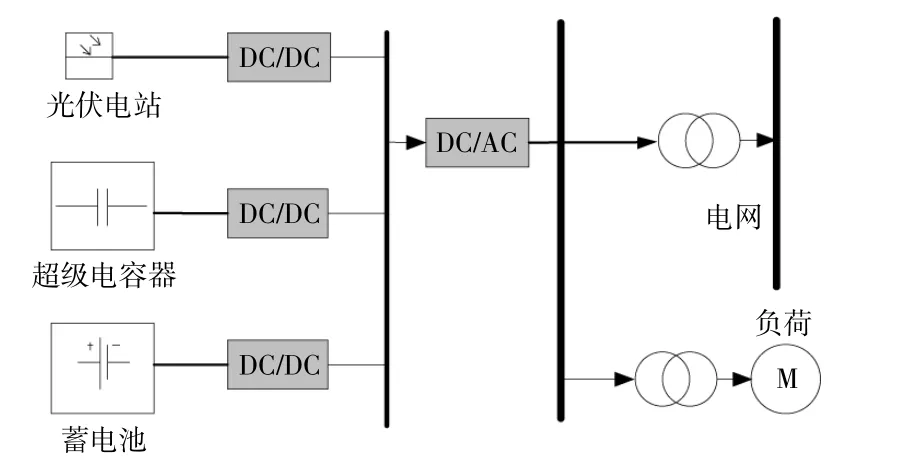
图5 光伏电站与复合储能系统Fig.5 Photovoltaic power station and composite energy storage system
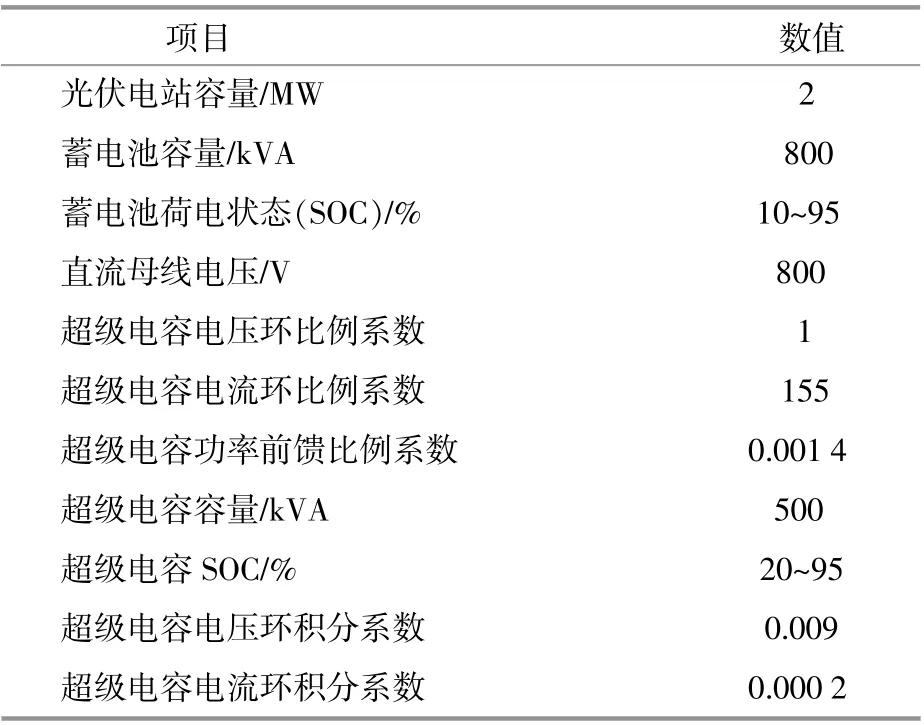
表1 系统参数Table 1 System parameters
设定工况:复合储能系统中的储能电量为额定电量的1/3,在第5秒时,光伏出力突然增加,此时蓄电池及超级电容充电。超级电容及蓄电池在充电过程中的荷电状态变化情况如图6所示。
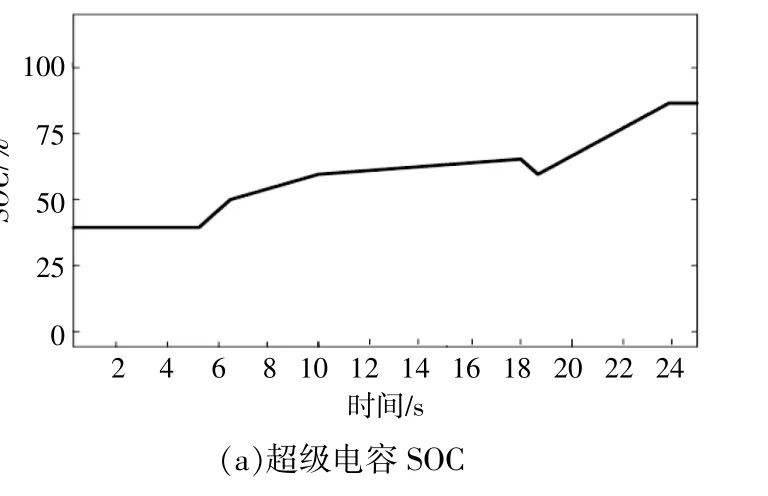

图6 超级电容与蓄电池荷电状态Fig.6 Battery and super capacitor state of charge
图7为控制前后的光伏出力波动曲线。由图7可以看出,利用改进量子粒子群算法,通过负荷储能的充放能协调,得到平抑后的光伏并网功率波动曲线的波动幅值变小,且在尖峰位置尤其显著。

图7 控制前后的光伏出力波动Fig.7 Control the fluctuation of photovoltaic output before and after
图8为母线电压波动情况。由图8可知,在第5分钟时,光伏出力突然增加,超级电容及蓄电池通过储能消纳多余电量,超级电容比蓄电池响应更快;超级电容可无延时响应电源出力变化,储能电池通过发出感性无功来抑制系统的电压升高,使得系统电压保持相对稳定。仿真结果显示,通过复合储能优化控制后,系统电压能够保持相对稳定,系统具有较好的高电压穿越能力。
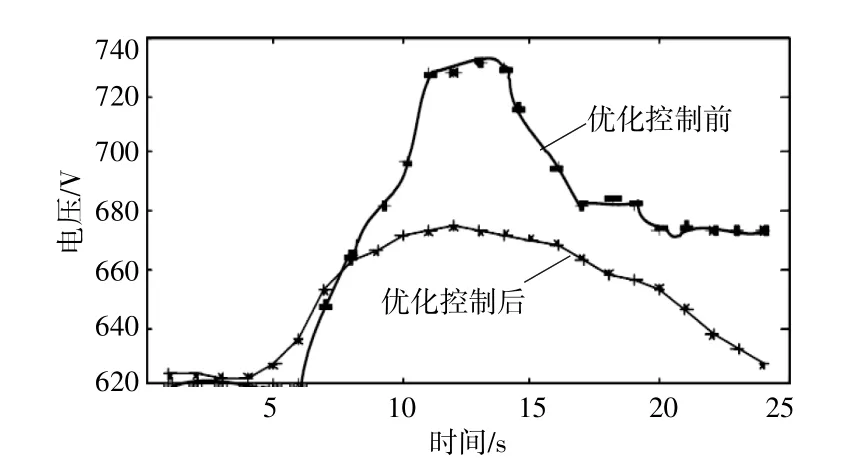
图8 母线电压波动情况Fig.8 Bus voltage fluctuation
当系统某日的光伏出力和负荷功率如图9所示,通过优化算法得到蓄电池储能与超级电容储能的功率分配如表2所示。
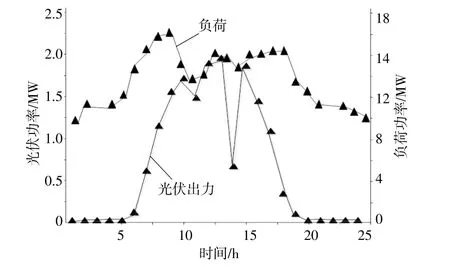
图9 光伏电站及负荷功率Fig.9 Photovoltaic power station and composite power

表2 储能配置结果Table 2 typical daily energy storage configuration results
通过双层优化控制,蓄电池以及超级电容的优化分配如图10所示。
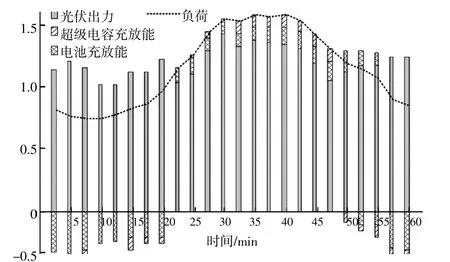
图10 蓄电池及超级电容的优化控制结果Fig.10 Optimal control results of batteries and super capacitors
系统频率变化标幺值如图11所示。由图11可知,当光伏电站出力突然增加时,蓄电池与超级电容吸收光伏电站发出的多余有功出力,共同维持系统稳定。仿真结果表明,采用基于量子粒子群优化的控制方法实现电池储能与超级电容储能的优化控制,可在一定程度上提高光伏电站并网节点电压的稳定性。

图11 并网点频率变化标幺值Fig.11 Grid-connected frequency variation per unit value
5 结束语
本文研究了复合储能系统中蓄电池和超级电容充放能特性,通过建立的复合储能协调的双层优化控制策略,实现了储能电池与超级电容协同配合。通过改进粒子群优化控制算法,可快速得到储能装置的充放电功率及容量,实现了光伏电站与复合储能一体化电网电压的稳定性控制。
