基于可再生能源汇集母线电压角速度轨迹的级联断面解列策略

张文朝，刘新元，张立伟，3，樊茂森，3，施浩波

（1.北京科东电力控制系统有限责任公司，北京 100192；2.国网山西省电力公司电力科学研究院，山西 太原030012；3.华北电力大学，北京 102206；4.中国电力科学研究院有限公司，北京 100192）

0 引言

近年来，随着可再生能源大规模接入以及特高压、直流通道的建设，我国电网结构的区域性和互联性加强，使大型互联电网潮流分布更加合理，电力交换更加便捷[1]～[3]。大功率可再生能源输送线路应用的同时，也伴随着严重的故障不平衡功率问题，甚至会引发大停电，威胁系统安全[4]。失步解列作为防止系统崩溃的最后一道防线，其解列策略的合理性和高效性尤为重要[5]～[8]。特别是当故障发生在可再生能源发电输送功率相互影响的级联断面上时，不完善的可再生能源解列策略可能会引发连锁故障，扩大事故范围。因此，为满足级联断面的安全稳定要求，须提出更加简单、快捷、准确的可再生能源汇集点解列策略。

目前，级联断面失步解列策略的主要研究热点为振荡中心定位及解列断面选择。关于振荡中心的定位问题，文献[8]应用无功功率积分的方法来推导振荡中心位置，能较好地确定振荡中心所在线路，但判据的有效性基于较好的积分起点，局限性较大。文献[9]应用可再生能源汇集母线电压频率的方法定位失步中心，且判据实现简单，不受电网结构限制，其PMU数据丰富，数据源较易获取。然而，该文献未明确振荡中心变化规律，没有进一步分析角速度轨迹与振荡中心分布的关系[10]。关于解列断面的选择，文献[11]在振荡中心的基础上将解列后孤岛不平衡功率引入目标函数进行解列断面选择，以此降低切机、切负荷量。文献[12]增加潮流冲击函数来降低解列操作对系统稳定的影响。上述文献均为单一或附加的解列策略，未能针对可再生能源易受扰动影响的特点给出合理的解列断面选择综合决策。

本文基于异步振荡过程可再生能源汇集母线角速度变化规律，确定了电势幅值比、角速度差等因素对振荡中心与失步中心的敏感性，推导出振荡中心电压角速度变化轨迹；应用短路阻抗法确定各可再生能源汇集线路角速度轨迹参数；针对可再生能源抗干扰能力差的特点，综合失步中心位置、振荡中心分布、孤岛不平衡度以及潮流冲击，应用主成分分析法决策级联断面解列方案。本方法在同步运行与系统不平衡功率尽可能小的解列原则上，加入潮流冲击指标以降低解列操作对可再生能源的影响；引入数学决策方法来提高解列方案的合理性。

1 级联断面耦合关系

当系统发生异步振荡时，根据可再生能源汇集点的同调分群情况，可以等效为双机系统或单机无穷大系统。以双机系统为例，等值后的系统图1所示。图1中：EM，EN分别为可再生能源汇集点和系统等值电势幅值；ZM，ZN分别为等值内阻抗；ZL为线路阻抗；δM为送端可再生能源汇集点等值机组相对于受端参考机组的功角；MM，MN为送受端系统等值惯性时间常数；IM，IN为母线三相短路电流；I1，I2为相应分支短路电流；Is1，Is2为系统侧提供的短路电流；J为线路MN上的任意一点。

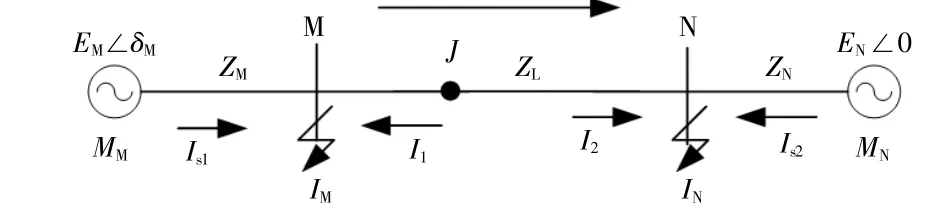
图1 等值双机系统图Fig.1 Equivalent two-machine system diagram

假设线路阻抗均匀，全系统阻抗角相等，且阻抗不随频率变化。当系统发生异步振荡时，母线M，N的电压功角可表示为

式中：MM，MN为两侧同调机群惯性时间常数；δM，δN为发电机功角；Mi，Mj和δi，δj分别为等值发电机惯性时间常数及功角。

若两同调系统断面某通道存在多条链式线路，且各线路间输电能力相互影响，则认为此断面为级联断面。以单通道为例，若级联断面共存在v级，则系统如图2所示。图2中：Uk，δk（k=1，2，…，v）分别为级联断面各可再生能源汇集母线电压幅值及相角；Xk为线路电抗；Xs1，Xs2为两端线路电抗。

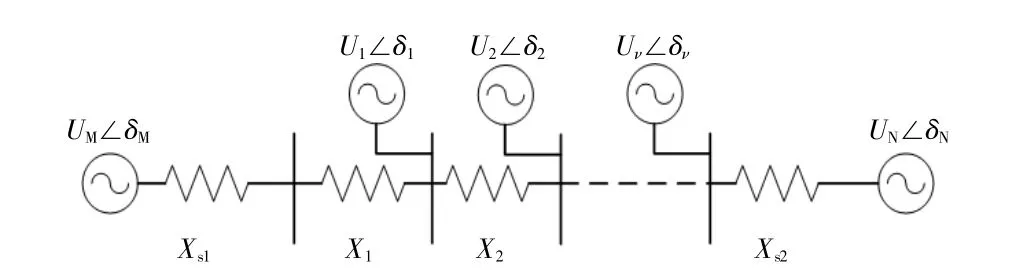
图2 单通道级联断面示意图Fig.2 Schematic diagram of single channel cascade

根据送受特性及发电机惯性时间常数，各母线功角为

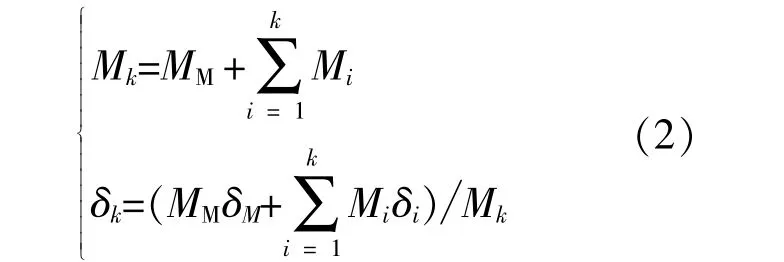
式中：Mk为前k级断面等值惯性时间常数；δk为第k级母线功角；Mi，δi为第i级断面等值惯性时间常数。

由断面潮流变化ΔP=（Δsinδ）/X可知，某一断面的解列将会引起相邻线路较大的潮流变化。此外，潮流变化与功角变化同步，可通过功角变化速率来表征系统功率振荡情况。功角变化速率可用角速度来表示，母线k处的角速度为式中：ωM为送端机组等效角速度；ωi为第i级母线角速度。

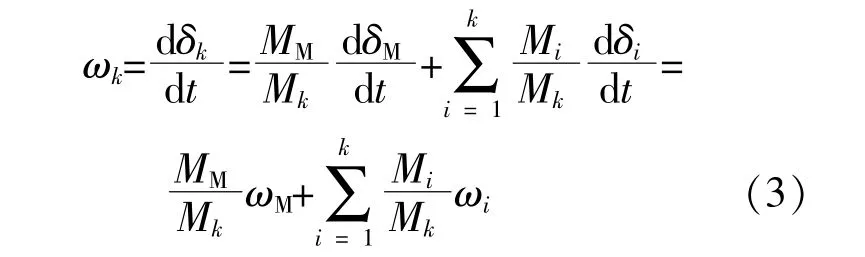
级联断面可再生能源汇集母线电压角速度可由送端机组惯性时间常数及角速度表示。当系统发生异步振荡时，发电机的角速度变化规律与机组惯量及加速功率有关。

式中：ω0为额定角速度；Pn为额定功率；TJ为发电机等值惯性时间常数；Pe为电磁功率；Pm为机械功率。

额定角速度ω0、额定功率Pn和发电机等值惯性时间常数TJ均为固定值。当电磁功率Pe偏离机械功率Pm时，发电机功角会随加速功率周期性摆动，造成角速度增率也随之周期性波动。

2 振荡中心及其迁移特性

系统发生异步振荡后，两同调机群功角在0～2π呈锯齿波变化，两侧系统角速度差不为零，系统各处电压、电流按一定频率振荡。以图1所示的等值双机系统为例，分析异步振荡过程可再生能源汇集母线电压角速度变化规律。

各变量关系如图3所示。为便于分析，在异步振荡短时间内认为两侧系统角速度差不变。

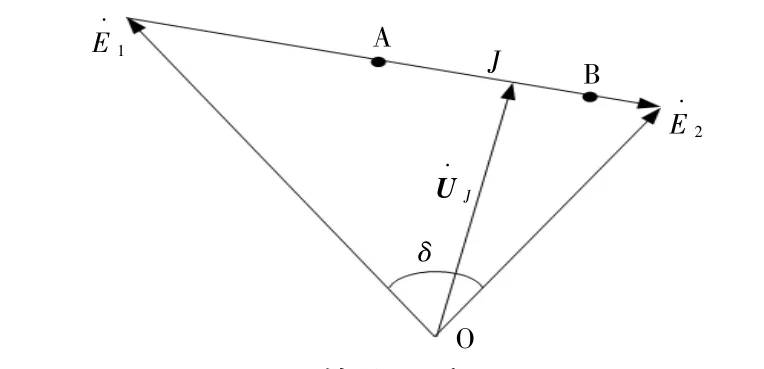
图3 等值系统矢量图Fig.3 Equivalent system vector

根据振荡过程各电气量变化规律及正、余弦定理可得J点的可再生能源汇集母线电压向量：

影响可再生能源汇集母线电压角速度的因素：测量点位置kJ、两端电势幅值比kE、两端角速度差Δω和时间t。为确定各因素对电压角速度的影响规律，绘制了如图4所示的角速度偏移量敏感性分析图。

图4 角速度偏移量敏感性Fig.4 Angular velocity offset sensitivity

图4（a）为kE=1.0，Δω=1 rad/s时，不同位置kJ的角速度与时间的变化规律。角速度随电气距离的变化关于失步中心对称分布；送端侧角速度升高，受端侧角速度下降；距离振荡中心越近，母线角速度偏差幅值越大。

图4（b）表征了Δω=1 rad/s，t=πs时，两端电势幅值比kE对振荡中心的影响。角速度随测量点突变的位置即为失步中心位置。随着kE的变化，失步中心总是向等值电势幅值较低的系统侧移动。

图4（c）为设置kE=1.2，kJ=0.5时，不同角速度差Δω下母线角速度变化情况。由图4（c）可知，Δω的变化仅影响可再生能源汇集母线电压角速度振荡周期，对振幅及振荡趋势无影响，不会造成振荡中心或失步中心偏移。

图4（d）为kE=1.0，Δω=1 rad/s时，可再生能源汇集母线电压角速度随时间的变化速率。一个振荡周期内，角速度在（0，π）区间不断增加，在（π，2π）区间不断减小，极大值点位于δ=π处，极小值点位于δ=0或δ=2π处；距离振荡中心越近，角速度变化速率越快；失步中心两侧角速度的变化速率相反。

3 基于主成分分析法的解列策略

为保证解列方案的合理性，除振荡中心、失步中心外，本文引入潮流冲击和孤岛不平衡度来综合决策解列方案[12]，[13]。

孤岛不平衡度表征解列操作产生孤岛中发电和负荷功率的不平衡程度，若解列后产生的孤岛个数为k，孤岛不平衡度IVi可表示为

孤岛不平衡度反映了解列后孤岛子系统的功率缺额或富余，不平衡度IVi越低，系统解列后各子系统越易控制。

潮流冲击为解列操作本身功率交换引发的功率冲击，潮流冲击较大时会威胁解列后系统的安全稳定。潮流冲击的计算式如下：

式中：Pij为不属于同一孤岛的母线i到母线j之间的功率值，即解列操作相关线路功率之和。

采用主成分分析法的主要计算过程：首先通过计算各解列方案中可再生能源汇集母线失步中心、振荡中心、孤岛不平衡度、潮流冲击等4个数据指标的相关性；按照信息贡献率提取出新的可再生能源电网主成分指标；将信息贡献率作为新指标权重，计算各可再生能源电网级联断面解列方案的综合评价值[14]。主要计算步骤如下。

①数据标准化处理

式中：λl为第l个特征值；yl为第l个主成分；v为主

4 仿真算例

西北青新联网750 kV网架如图5所示。该电网由XJ（新疆）子网、GS（甘肃）子网、QH（青海）子网、NX（宁夏）子网及SX（陕西）子网5部分构成。网内风电装机容量52 770 MW，光伏装机容量45 690 MW。XJ子网、GS子网、QH子网间存在两通道级联断面，分别为QW～JQ～HX（ZY）北通道和SZ～YK～CD南通道。按风电同时率为0.5，光伏同时率为0.8考虑，某方式下XJ子网外送功率3 000 MW，SX+NX子网受电10 900 MW。北通道主要为风电汇集母线，新能源汇集上网容量为6 700 MW；南通道主要为光伏汇集母线，新能源汇集上网容量为8 700 MW。

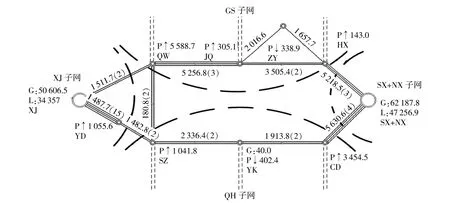
图5 某电网地理接线图Fig.5 A geographical grid connection diagram

当XJ子网内0 s发生直流线路3次换向失败闭锁故障，并于0.68 s切除故障时，以SX子网BE发电机为参考机的各子网功角曲线如图6所示。由图6可知，XJ子网全部机组相对系统发生异步振荡，部分GS子网内小机组功角失稳，但与XJ机组不同调。

图6 异步振荡过程功角曲线Fig.6 Power angle curve of asynchronous oscillation process

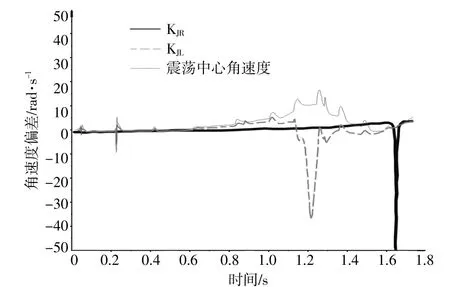
图8 下通道角速度偏差Fig.8 Lower channel angular velocity deviation

级联断面各可再生能源汇集母线电压角速度如图7，8所示。因部分GS子网机组的不同调振荡，导致曲线存在小幅波动。母线SZ与YK及JQ与HX（ZY）电压角速度变化速率相反，异步振荡失步中心位于SZ～YK线路和JQ～HX（ZY）线路上。振荡中心轨迹相关信息列于表1。

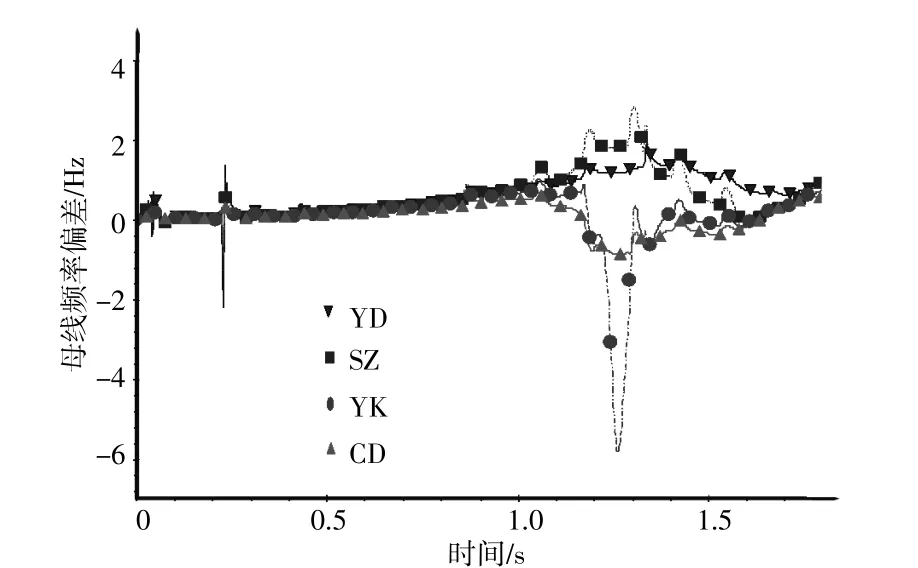
图7 母线频率偏差Fig.7 Bus frequcncy deviation

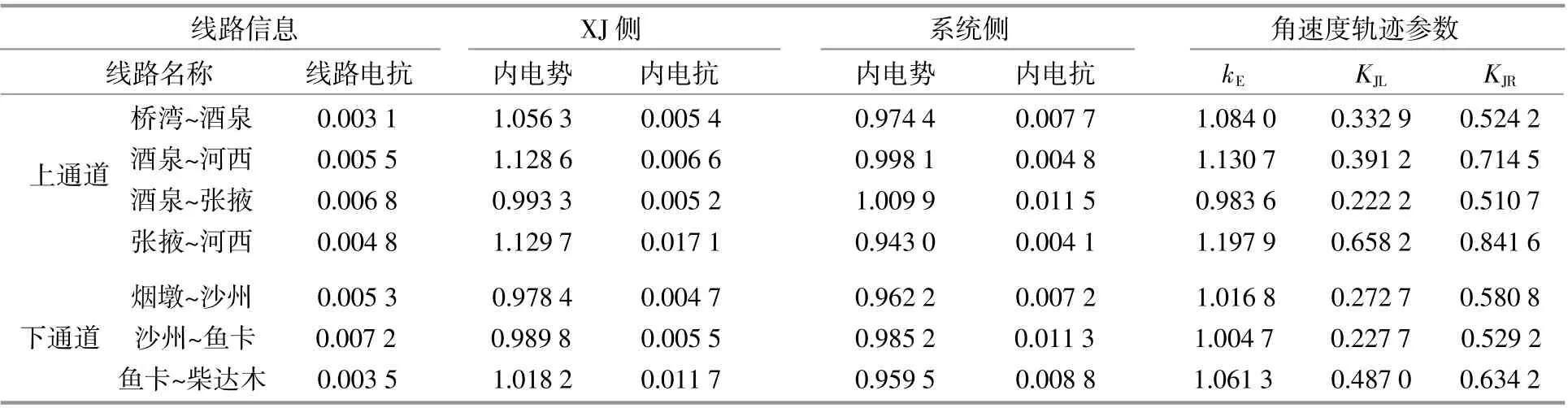
表1 振荡中心轨迹相关信息Table 1 Information about the oscillation center trajectoryp.u.

根据下通道级联线路是否能构成解列断面，计算级联断面各解列方案。

故障解列时间为0.68 s时，XJ子网直流线路3次换向失败闭锁故障消除。1.17 s各可再生能源汇集母线电压角速度摆开，解列装置启动。1.71 s时第一个振荡周期完成。解列方案判定为SZ～YK及JQ～（HX）ZY线路，实施解列后两侧系统功率如图9所示，系统稳定，无连锁故障发生。

图9 实施解列操作后系统两侧线路功率Fig.9 Line power on both sides of the system after the implementation of the unpacking operation

将本文提出的解列方案求解算法的计算时间与文献[13]和文献[15]中的解列计算方法进行对比，结果如表2所示。由表2可以看出，本文采用主成分分析法对可再生能源电网级联断面解列策略进行求解，解列方案计算时间最短，提高了可再生能源电网级联断面解列策略的计算效率。

表2 采用不同解列方案计算方法对比Table 2 Principal component analysis results table

5 结语

本文直观、高效地以失步过程中可再生能源汇集母线电压角速度变化速率相反来确定失步中心位置，以振荡中心电压角速度轨迹扫过的范围来确定振荡中心分布。应用失步中心、振荡中心、孤岛不平衡度和潮流冲击4个指标，更好地反映了解列方案的有效性及对解列后孤岛系统的影响，有利于评估可再生能源的受扰动程度。应用本文提出的主成分分析法决策解列方案，可以提高计算合理性与计算效率。通过西北电网的仿真实例显示，所提策略实现过程简单、现象结果直观，仅根据母线参数即可确定振荡中心位置，且解列断面选择原则全面、合理，解决了同步运行与解列后的稳定性问题。