空腔流动的动量分解及能量输运特性1)

2022-03-20韩帅斌武从海张树海

力学学报 2022年2期

韩帅斌罗勇李虎武从海张树海

(中国空气动力研究与发展中心,空气动力学国家重点实验室,四川绵阳 621000)

(中国空气动力研究与发展中心,计算空气动力研究所,四川绵阳 621000)

引言

空腔是一种非常具有代表性的结构,广泛应用于航空航天飞行器部件及地面交通工具中,如飞机的起落架舱、航空发动机内部凹槽以及高速列车受电弓腔、汽车天窗等[1].空腔流动结构复杂,存在剪切层和旋涡,对超声速流动还会产生激波,是一种重要的噪声源,也是相关工程设计中必须考虑的关键问题.

空腔流场中各种结构之间的相互作用会产生丰富的非线性物理过程,包括多模态共振、涡声的产生和传播、多波相互作用等.在亚声速空腔流动中,剪切层、旋涡和声波等流动结构之间的相互作用占据主导地位;超声速空腔流动中则存在复杂的激波波系,激波之间、激波与其他流动结构之间相互作用会产生激波噪声[2-3].空腔噪声的产生涉及以下动力学过程:起始于空腔前缘的涡扰动在剪切层内不断增长并向下游对流,对流至空腔后缘点处的涡与后缘点相互作用从而产生向外辐射和向上游传播的声波,声波扰动到达前缘点并进一步诱发新的涡扰动.在以上动力学过程中,腔体内形成扰动反馈增长回路,主流中的动力学能量不断转化为声能,产生的强噪声持续向外辐射.

在空腔流动中,流体动力学模态(涡模态和熵模态)与声模态之间的相互作用是空腔自持振荡的重要过程,二者在近场的耦合作用机制对流动的发展和演化起着关键作用[4].在低速流动中,熵模态通常较弱,涡声模态之间的相互作用构成了流动的主要机制.Kerschen 和Tumin[5]与Alvarez 等[6]基于空腔边缘散射机制,建立了超声速和亚声速空腔声模态与剪切层内涡层在空腔前后缘相互作用并转化的理论模型,预测了涡波和声波的幅值和相位变化;Tang和Rockwell[7]研究了涡与空腔后缘相互作用形式对瞬态压力场的影响,发现压力幅值及相位与涡-缘相互作用形式密切相关;万振华[8]基于涡量和拟涡能分析了空腔内涡结构撞击空腔后缘点产生脉动压力的动力学过程;韩帅斌等[9]采用拉格朗日拟序结构分析了空腔流动中涡的生成、对流、撞击和破裂等动力学过程.随流动马赫数增加,流动可压缩性增强,熵模态扰动也随之增强.Arya 和De[10]基于声学扰动方程(acoustic perturbation equation,APE)分析了可压缩空腔流动中的Lamb 矢量所代表的涡声源和熵的时空扰动所代表的熵声源对噪声产生的贡献,发现熵声源对于远场和近场声压均具有一定影响;Liu 和Gaitonde[11]基于预解分析(resolvent analysis)对亚声速和超声速空腔流动中涡熵动力学模态和声模态的激励响应特性进行了研究.

已有的研究基本上都采用不同的变量分别表征流声模态,并未对同一流动变量进行流声模态分解,无法深入理解流声模态之间的相互作用及不同模态之间的能量转化机制.准确识别并解耦空腔内的流体动力学模态和声模态,是深入理解空腔流声相互作用和能量转化机制的关键.对于任意一个矢量场,亥姆霍兹分解可将其分解为无旋有散的标量梯度场和一个有旋无散的向量旋度场[12-13].针对速度场,前者表征涡模态速度,对应于旋涡结构;后者则是流体可压缩性的体现,在等熵流中可表征声模态速度,对应于声波、激波、膨胀波等可压缩流动结构.针对速度场的传统亥姆霍兹分解在矢量气动声学[14]、可压缩湍流[15]中得到了广泛应用.然而传统亥姆霍兹分解无法解耦速度场中的熵模态,仅能应用于等熵流动.Doak[16]提出了针对动量的亥姆霍兹分解,并建立了动量势理论(momentum potential theory,MPT).MPT 将动量分解为涡(有旋无散量)、声(无旋等熵量)和熵(无旋等压量)3 类组分,系统分析了各类组分相互作用的能流特性.目前MPT 已被广泛应用于波包动力学[17]、射流[18-19]、钝体绕流[20-21]以及边界层转捩[22-23]等,揭示了相应流动中不同模态的流动特性.

本文针对来流马赫数Ma=0.8 的二维亚声速空腔流动进行数值模拟,获得高精度流场数据.基于MPT 对空腔流动的动量进行分解,得到动量的涡熵动力学组分和声组分,研究各组分动量的时空特性,试图分析并揭示不同组分相关的能量输运特性.

1 数值及理论方法

1.1 空腔流动高精度数值模拟

在文献[9,24]中,已经对空腔的流场结构进行了高精度数值模拟,并进行了网格收敛性验证和计算结果与文献对比验证.在数值模拟中,控制方程为二维Navier-Stokes 方程,其具体形式为

式中 ρ,u,p,E,σ,T,μ,Re,Pr,M 分别为密度、速度、压力、能量、黏性应力张量、温度、动力学黏性系数、雷诺数、普朗特数和马赫数.

无量纲过程中的参考长度为空腔深度,速度的参考值为无穷远处声速,密度、压力、温度等流场变量的参考值采用无穷远值.计算中,Navier-Stokes方程的对流项采用五阶WENO 格式[25-27]离散,黏性项采用6 阶中心差分格式离散,时间推进采用3 阶TVD Runge-Kutta 方法.

空腔流动数值模拟的计算区域如图1 所示,其中空腔长深比为2:1,各长度参数为:L=2D,Ll=7D,Lr=20D,Ly=20D,Li=3D,Lo=10D,Lt=10D.空腔来流马赫数为Ma=0.8,普朗特数为Pr=0.7,雷诺数为Re=2500.在数值模拟气动声学问题时,由于声学扰动是小量,远场边界处微弱的声波反射即可引起较大的数值计算误差,因此本文采用Bodony[28]的方法,在计算域外缘设置海绵层从而降低边界上声波的反射,避免声场污染.数值计算网格量为:腔外网格810×300,腔内网格240×120,其中固壁边界处的网格进行了加密处理以捕捉边界层,远场网格进行拉伸以降低反射[29].数值模拟所得的流场纹影如图2 所示,清晰显示了空腔流动的远场声场和近场剪切层及涡结构.对空腔(1.0D,1.0D)处的速度和压力脉动采样分析,可得流动的无量纲时间周期为T=3.75[9],相应的无量纲频率St=fL/U=0.67,与Rossiter 半经验公式给出的第二模态频率St2=0.686 和Krishnamurty[30]的实验结果St=0.656 吻合.网格收敛性验证和计算结果的准确性验证可参考文献[9,24].

图1 空腔流动数值模拟计算区域Fig.1 The computational domain of open cavity flow for numerical simulation

图2 空腔流动的数值纹影Fig.2 Numerical schlieren of open cavity flow

1.2 动量势理论

MPT 由Doak[16]提出,通过对动量应用亥姆霍兹分解,将动量分解为有旋无散的涡动力学量、有散无旋的声学量和熵动力学量,具体为

其中B0为时间平均的动力学量,B′为脉动涡动力学量,ψ 为脉动标量势,表征流动的可压缩特性,包含了声组分和熵组分.结合连续性方程

可得标量势满足泊松方程

基于以上分解,动量可视为时间平均动力学量、涡组分、声组分和熵组分4 个部分的线性叠加.通过求解式(5)和式(6)中任意两个泊松方程即可获得流场中动量的不同组分.由于压力和密度为流场的原始变量,较易通过求解获得其时间导数,因此本文通过求解总标量势泊松方程(5)和声标量势泊松方程(6b)进行动量分解,其具体实现步骤如下:

(1)对周期性或准周期性流动,依据流场变量的时间演化获得其流动周期T,并对一个流动周期[t0,t0+T]内的动量 ρu 进行时间平均,由此获得B0;

(2)对流场进行时间微分获得 ∂ρ′/∂t,求解泊松方程(5)获得标量势 ψ ;

(3)对流场进行时间微分获得 ∂p′/∂t,并计算当地流体声速 c2=γp/ρ,求解泊松方程(6b)获得声标量势 ψA;ψT=ψ-ψA

(4)计算熵标量势 ;B′=ρu-B0+∇ψ

(5)计算无散的涡组分 .

在空腔流动的动量分解过程中,泊松方程的求解采用Gauss-Seidel 迭代方法,每次迭代包括交替方向的两次扫描.初始条件和边界条件设置可参考文献[18,20-21],具体为:标量势 ψ 的初始条件设为ψ0=0;边界条件设置为:左边界、上边界和右边界采用远场边界(由图3 中不同高度处动量脉动的旋度 ∇×(ρu)′的分布可知,∇×(ρu)′的幅值从近场到边界处由 O(1) 衰减至 O(10-4),说明在边界处动量脉动几乎不存在有旋组分),可令有旋无散脉动量B′=0[18,21],于是由式(3a)有(ρu)′=-∇ψ,因此沿边界积分即可实现对远场边界的赋值,即远场边界施加狄利克雷边界条件;对于物面边界,设置法向零梯度边界条件,即诺依曼边界条件.求解 ψA时,远场边界赋值为 ψA=ψ,物面边界则赋法向零梯度边界条件.

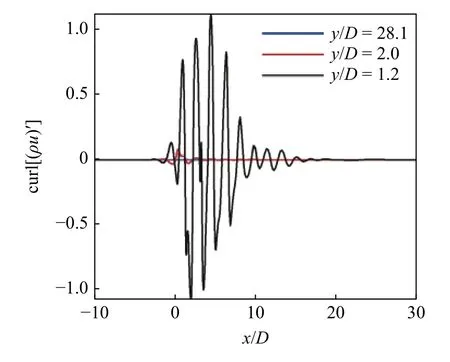
图3 不同高度处动量脉动的旋度分布Fig.3 The distribution of the curl of momentum perturbation

在以上动量分解的基础上,能量守恒方程的时间平均可写为如下形式

其中 H=cpT+u·u/2 为总焓;α′为加速度脉动,由流动中的涡量扰动、熵空间不均匀性以及黏性应力所贡献.上式左端项表示动量的涡声熵各组分所携带的脉动总焓的时均流量,右端则是输运过程中各组分动量与加速度脉动相互作用所形成的源,表示对流体微团做功的功率,影响左端平均能流的产生(正源)或耗散(负源).当流场中不存在某一类动量组分时,其对应的流量及源相应为零,因此基于式(7)可分析各动量组分相关的能量的产生与耗散机制以及能量的输运与转化特性.

2 方法验证

首先验证泊松方程求解方法.图4 给出了空腔内不同站位处泊松方程(5)左右端数值结果,两者吻合很好,且方程两端残差的数量级为 O(10-7),数值求解取得了较好的收敛效果.

图4 不同位置处泊松方程(5)左右端项分布Fig.4 The distribution of LHS and RHS of Eq.(5) at different locations

其次验证动量分解所得各组分的物理属性.图5 给出了空腔上方y=1.2 处的时间平均动量、涡组分动量以及可压缩组分动量的散度分布.由散度分布可见,时均动量和涡组分动量的散度均几乎为零,其中在空腔附近[0,5]的流动旺盛区域,由于流动的空间不均匀性,时均动量和涡组分动量的散度均存在非零扰动,但二者最大幅值均为 O(10-3),远远小于 ∇2ψ 的量级O (10-1),因此可认为采用MPT成功实现了动量的无散动力学量和有散可压缩量的分离.

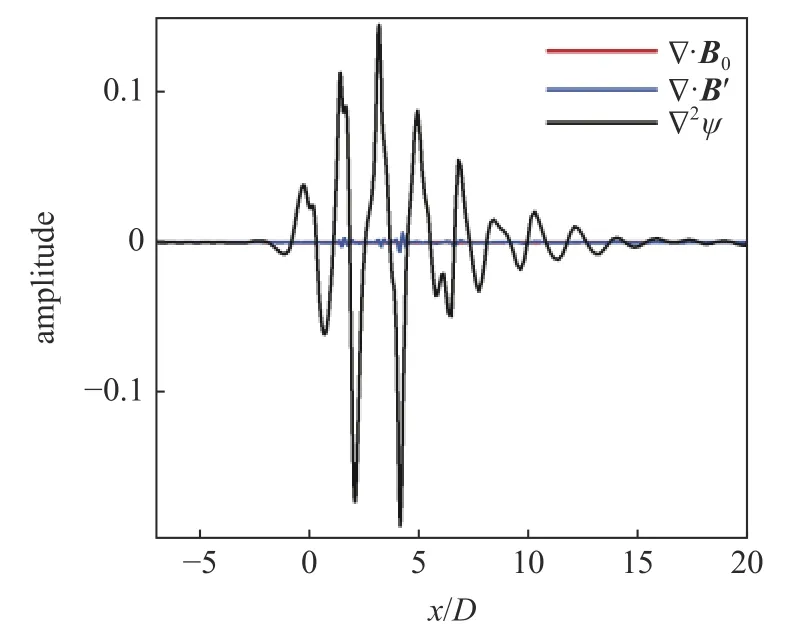
图5 y=1.2 处不同组分的散度分布Fig.5 The divergence of different components of momentum at y=1.2

采用快速傅里叶变换(FFT)对密度、速度、原始动量以及MPT 分解所得各组分动量的频谱特性进行对比验证.对位于空腔(1.0D,1.0D)处的各变量进行FFT 分析,结果如图6 所示,各流场变量以及原始动量的频谱为离散频谱,主频均为St=0.67,其余峰值为主频的谐频,说明流动具有强周期性.MPT分解所得涡声熵组分动量的主频与原始变量一致,也为St=0.67,进一步证明了采用MPT 分解所得各组分的准确性.

图6 频谱分布Fig.6 Frequency spectrum

3 结果与分析

3.1 动量的流声组分特性

对空腔流动的流场应用MPT 进行动量分解,分析动量的声熵涡各组分空间分布特性、时间演化特性.图7 给出了标量势以及声熵涡各组分动量在一个流动周期内任一时刻的空间分布.其中声熵组分为动量的可压缩部分,其空间分布特性可由标量势表征.由图7(a)～图7(c)可知,总标量势 ψ 所表征的脉动主要分为3 部分:空腔剪切层附近同时包含声组分和熵组分的周期性胀缩脉动,空腔左上方强烈的声脉动和空腔右侧相对较弱的声脉动.声标量势ψA与总标量势 ψ 在远场几乎一致,说明动量的可压缩部分在远场仅包含声组分,而在近场由于熵组分的存在,声标量势与总标量势在空腔剪切层附近有所差异.熵标量势 ψT集中分布在空腔剪切层附近及空腔后方尾迹内,并呈现出周期性的压缩膨胀特征.

图7 动量不同组分的空间分布Fig.7 Spatial distribution of different components of momentum

动量的声熵涡组分在x 和y 方向的分量如图7(d)～图7(i)所示.声组分动量分布于空腔内以及远场.空腔内的声组分动量揭示了空腔自持振荡的声学脉动,其波阵面以近似垂直于空腔下壁面的平面波形式在腔体内传播,强度与腔外声波为同一量级,但高于腔外声波,与文献[8]中空腔内声压级高于腔外相一致;空腔外的远场波阵面分布则揭示了声波由空腔后缘点和前缘点向外辐射并传播的过程,其中空腔左侧声波波系由于入口均匀来流产生了明显的多普勒效应;空腔上方的波系较强,是空腔非定常流动产生的主要噪声,空腔右侧存在较弱波系,呈现为球面波形状.熵组分动量的空间分布模式与涡组分相似,两者均主要分布于空腔剪切层及空腔后缘点后的尾迹中,与剪切层内卷起的涡层及空腔右侧的主涡密切相关,但是熵组分动量强度比涡组分低1～ 2 个数量级,与声组分数量级接近.因此从强度看,在空腔流动的近场,涡组分动量为主要部分,主导着剪切层内涡层的发展演化;在远场则只存在声组分,揭示远场噪声的传播过程.

由动量的声熵涡组分在近场的空间分布可知尽管三者均呈现沿流向的周期性正负交替分布,但分布特性仍有差异.其中声组分以近似垂直于空腔下壁面的平面波形式分布,并在空腔内振荡传播,而熵涡组分则集中于剪切层,以波包形式存在,随主流向下游对流.为了揭示三者的传播速度,对空腔唇口线上(x ∈(0,2D),y=1D) 的各组分动量在一个流动周期内的时空演化特性进行分析.图8(a)～图8(c)分别为声熵涡流向动量的的x-t 分布图,其中只有声组分动量呈现向上游传播的扰动,这是由空腔后缘点产生并向上游传播的声波,由于来流速度影响,其传播速度为为唇口线上流向速度的空间平均值,c∞=1 为单位无量纲声速;熵组分和涡组分动量则沿来流方向随着剪切层向下游传播,其传播速度均为 |dx/dt|=0.5 ≈Uc,这里 Uc≈L/T=0.53 为剪切层的平均对流速度.

图8 各组分流向动量的时空分布Fig.8 The spatial-temporal distribution of different components of momentum

3.2 动量流声组分相关的能量输运特性

涡声熵组分动量相关的能量输运特性可由式(7a)描述,其中左端项依次代表涡声熵组分动量所携带的总焓流量,右端项则是相应的源.对能量方程(7a)的左端项和右端项分别计算并对比,结果如图9所示,两者完全吻合,且计算的残差最大为 O(10-5),远小于各组分动量所携带的总焓流量的大小,证明了计算的准确性.同时由图9 可知,时均总焓流量分布可划分为5 个区域:I 区为涡卷起并充分发展的剪切层核心区,总焓流量为正;位于剪切层外侧的II 区和位于空腔后缘点左上附近的III 区总焓流量均为负,表明在剪切层内,动量所携带的总焓不断流出,随着剪切层对空腔后缘点的撞击,总焓不断向空腔后缘点附近汇聚,并向剪切层外侧传递能量.IV 区为空腔内右半侧的主涡区,在主涡内,总焓流量呈正负交替分布,主涡内整体呈现能量平衡状态,因而可保持稳定.V 区为空腔后缘点后的尾迹区,总焓流量沿垂直于流向方向正负交替分布,边界层内的能量不断向边界层外传递.

图9 能量方程左右端项Fig.9 Left hand side (LHS) and right hand side (RHS) of the averaged energy equation

图10 给出了能量方程左端涡声熵各组分动量所携带的总焓流量与相应源的分布.涡组分源分布主要集中于剪切层,呈现垂直于流向的正负交替的双层分布,并在后缘点附近形成负源,因此涡组分动量所携带的总焓由空腔前缘点起始,跟随剪切层的运动,从剪切层内不断输运至剪切层外侧以及空腔后缘点处.空腔内的主涡处交替分布了相对较弱的正负涡组分源,其能量的平衡使得空腔右侧主涡保持相对稳定状态.声组分动量所携带的总焓流量在剪切层内呈现出强度近似的周期性正负分布,空腔后缘点左侧区域总焓流量为负值,表明声组分动量携带的总焓流量由后缘点右侧不断流向该区域,并向上游和远场传播.声组分源仅存在于近场,在剪切层内沿流向呈周期性正负分布,且正源显著强于负源,因此声组分动量携带的总焓从剪切层内不断流出,以声能形式向外辐射;同时空腔右侧主涡附近也存在着强度相近的正负声组分源,表明空腔内的声自持振荡可以保持能量的稳定状态.熵组分动量与涡组分动量空间分布相似,均与剪切层密切相关;另一方面熵组分动量与声组分动量均具备可压缩特性,因此熵组分动量携带的总焓流量分布同时呈现出了类似于涡组分的垂直于流向的层状分布特性和类似于声组分的沿流向的周期性正负交替分布特性.熵组分动量携带的总焓流量由剪切层下方输运至剪切层核心区域,剪切层上方则沿流向周期性流入流出,保持平衡状态.熵组分源主要分布于剪切层附近,且主要为负源,因此熵组分动量携带的总焓不断向剪切层内输运,并在剪切层内耗散.

图10 能量方程各项空间分布Fig.10 The spatial distribution of various terms in energy equation

对比3 类动量组分所携带的总焓流量的强度可知,涡组分高于声组分和熵组分至少一个数量级,因而涡组分相关的能量输运过程在空腔流动中占据主导地位;声组分和熵组分数量级接近,尽管两者强度较小,但在空腔内的声能输运以及能量耗散过程中均起着重要作用.值得注意的是,涡声熵组分相关的能量方程左右端分布均有显著差异,其差值resi=RHSi-LHSi 如图11 所示,resi＞0 表示相应组分的源大于该组分的总焓流量,反之则相反,因此动量的涡声熵组分所携带的总焓流量与相应的源并非一一对应关系,在不同组分之间存在着能量的转化.为了量化分析各组分之间的能量输运特性,在图10(a)中的流动旺盛区域A 内对能量方程(7a)中的各项进行空间积分,获得该区域内各组分动量相关的能量的净流出/流入和净产生/耗散,结果如表1 所示.由左端项的净流量可知,涡组分动量携带动力学能净流出区域A,输运至空腔尾迹的边界层和空腔内的主涡内;声组分动量携带声能净流出,向远场持续辐射声波;熵组分动量则携带能量净流入至区域A 内.由右端项的净源可知,涡组分和声组分源均为正源,不断产生相应的能量,熵组分源则为负源,耗散流动中的能量.对比涡声熵各组分的净源和净流量可知,涡组分和声组分能量的净产生均高于其净流出,而熵组分的净耗散高于其净流入,因此由能量平衡可知,在剪切层内存在着涡声组分能量向熵组分能量的转化.