非线性多状态时滞系统容错保性能控制
2022-03-19温秀平耿冉冉
温秀平,耿冉冉
(南京工程学院工业中心、创新创业学院, 江苏 南京 211167)
现实世界中很多实际的系统往往都存在非线性和时滞,再加上元器件老化、关键部件失效等因素影响,在高负荷的运行过程中执行器或者传感器难免发生故障,这些因素的存在给控制器的设计带来了极大的挑战.对于实际系统,如果不能设计有效的容错控制器及时对故障系统进行控制,系统性能可能会下降,甚至出现系统不稳定的现象,严重时会造成较大的经济损失[1].因此,非线性时滞系统的容错控制问题已成为国内外学者研究与关注的热点.
目前,容错控制方法已广泛应用于无人机、电动汽车、卫星姿态系统、船舶等实际系统.文献[2]针对四旋翼无人机执行器发生偏差故障情况提出一种改进的分数阶幂次滑模容错控制算法,在有限时间内可以使系统达到稳定,有效克服了传统容错控制方法只能使系统渐进稳定的缺点;文献[3]研究了四轮独立驱动电动汽车系统在执行器故障和不匹配干扰条件下的跟踪控制问题,提出一种自适应快速终端滑模容错控制方案;文献[4]研究了卫星姿态系统执行器含有混合故障时的容错控制问题,提出一种基于迭代学习观测器的姿态跟踪容错控制方法;文献[5]针对船舶航速/航向协调控制系统,提出一种非线性广义扰动观测器,并基于自适应估计与广义扰动补偿提出一种自适应滑模容错控制方法,在冗余舵桨系统发生故障情况下,实现了广义扰动补偿、航速/航向跟踪和执行器能耗最优化.
近年来,关于非线性时滞系统容错控制问题的研究已经取得了一些成果,但也存在一些问题有待解决.文献[6]针对可反馈线性化非线性系统,研究了系统存在未知不匹配干扰和不确定执行器故障时的容错控制问题,提出一种鲁棒自适应容错控制策略,同时针对系统各种故障分别设计容错控制器,融合得到一个综合故障补偿控制器,有效解决多重不确定执行器故障情况,保证闭环系统的稳定性及获得期望的性能;文献[7]针对满足Lipschitz条件的非线性系统,研究了系统执行器发生故障时的容错控制问题,提出一种鲁棒滑模容错控制方法;文献[8]研究了具有未知控制系数和执行器故障的非线性严格反馈领导-跟随系统在固定有向图下的自适应协同容错监控问题;文献[9]研究了一类同时具有参数不确定性和时滞的非线性系统的鲁棒容错控制问题,基于线性阵不等式方法给出了闭环系统渐进稳定的充分条件及控制器的设计方法;文献[10]针对具有执行器故障的不确定奇异时滞系统,研究其容错控制问题,给出了故障闭环系统渐进稳定的充分条件,所设计的容错控制器可以满足无源性能指标.文献[6-8]均研究了非线性系统的容错控制问题,但未考虑时滞对系统的影响;文献[9-10]针对不同系统的容错控制问题设计了有效的控制器,但主要研究了单一时滞情况,未考虑系统具有多个状态时滞时的容错控制问题.
综上,同时考虑非线性、多时滞、执行器故障及性能指标的约束等问题综合设计容错控制器极为少见.因此,本文主要研究一类具有多个状态时滞且满足Lipschitz条件的非线性连续系统的执行器发生故障时的容错控制器及容错保性能控制器的设计.当系统发生执行器故障时,分别设计容错控制器和容错保性能控制器,基于线性矩阵不等式方法(linear matrix inequality,LMI)给出故障闭环系统渐进稳定的充分条件,并利用Lyapunov稳定性理论分析证明系统的稳定性.本文设计的优点在于:1) 同时考虑非线性、多时滞、执行器故障及性能指标约束等问题设计容错控制器;2) 文中设计的容错控制器和容错保性能控制器可以同时保证执行器正常工作和发生故障情况下系统的渐进稳定性;3) 容错保性能控制器可以满足给定二次型性能指标的要求;4) 系统收敛速度快.
1 问题描述
考虑具有多个状态时滞的非线性连续系统:

(1)
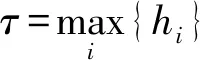
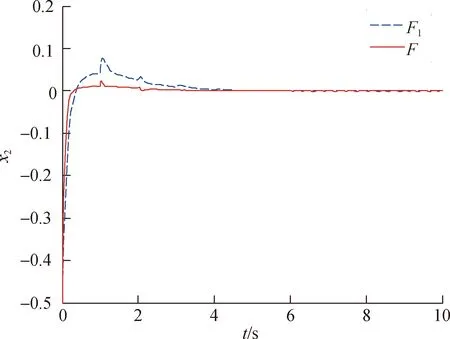
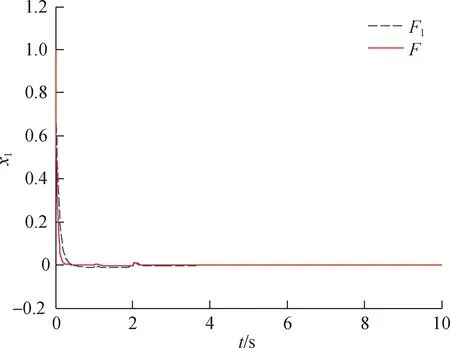
定义执行器故障矩阵F=diag(f1,f2,…,fm),0≤fi≤1(i=1,2,…,m).当fi=0时,表示第i个执行器完全失效;当0 针对式(1)系统,在执行器发生故障的情况下,设计状态反馈容错控制器的形式为: u(t)=FKx(t) (2) 式中:F为执行器故障矩阵;K为待设计的控制器增益矩阵. 将式(2)代入式(1),则可得故障闭环系统状态方程为: (3) 对于系统(1),在执行器发生故障的情况下,选取二次型性能指标: (4) 式中,Q、R为给定的对称正定加权矩阵. 本文目的是针对非线性多状态时滞系统(式(1)),设计状态反馈容错控制器(式(2)),使得对于所有可能发生的执行器失效故障,故障闭环系统(式(3))渐进稳定,且满足性能指标(式(4)). 引理1[11]对于适当维数的矩阵X和Y,以及标量ε>0,有: XTY+YTX≤εXTX+ε-1YTY (5) 假设1[12]非线性函数f(x(t))满足Lipschitz条件,即存在常数l>0,使得: (6) 并且满足f(0)=0. 定理1对于故障闭环系统(式(3)),如果存在正定对称矩阵X和矩阵Y,对于给定的常数l>0,εi>0(i=1,2,…,n+2),满足矩阵不等式: (7) 证明:选取Lyapunov函数为: (8) 式中:P>0;Qi(i=1,2,…,n)待求. 沿故障闭环系统(式(3))对V(x(t),t)求导可得: wT(t)DTPx(t)+xT(t)PDw(t)+fT(x(t))Px(t)+ (9) 根据引理1可得: (10) 同理可得: wT(t)DTPx(t)+xT(t)PDw(t)≤ (11) 再由引理1和假设1可得: fT(x(t))Px(t)+xT(t)Pf(x(t))≤ (12) (13) 根据Lyapunov稳定性理论知,只要式(14)成立: (14) 则故障闭环系统(式(3))渐进稳定.将(14)式分别左乘、右乘diag(P-1,P-1),并令X=P-1,Y=KX,再根据舒尔补性质可知其与式(7)等价,从而定理1得证. 定理2对于故障闭环系统(式(3))和性能指标(式(4)),如果存在正定对称矩阵X和矩阵Y,对于给定的常数l>0,εi>0(i=1,2,…,n+2),以及正定对称加权矩阵Q和R满足矩阵不等式: (15) 证明:与定理1证明过程类似,选取Lyapunov函数为: V(x(t),t)=xT(t)Px(t)+ (16) 式中P>0.由定理1证明过程可知,沿故障闭环系统(式(3))对V(x(t),t)求导,并根据引理1和假设1可得: (17) 如果式(18)成立: xT(t)[(A+BFK)TP+P(A+BFK)+ (18) 则有: (19) 成立.根据定理1的证明过程易证式(15)成立等价于式(18)成立.根据Lyapunov稳定性理论可知,故障闭环系统(式(3))渐进稳定. 进一步,对式(19)两边对时间t从0到∞积分,并利用系统的渐进稳定性,可得: (20) 即满足J≤J*,定理2得证. 考虑形如式(1)的非线性多状态时滞系统,取: 定理1中取: n=2,ε1=ε2=ε3=ε4=l=1, 利用Matlab软件LMI工具箱求解式(7)可得: 同样地,定理2中取: n=2,ε1=ε2=ε3=ε4=l=1, 利用Matlab软件LMI工具箱求解式(15)可得: J*=2.122 6 根据上述结果在Simulink中建模仿真,设t<0时,x(t)=φ(t)=0,选取x0=[1,-0.5]T,分别得到定理1和定理2对应的状态响应曲线. 图1为无性能指标约束时系统发生F1故障及正常工作时状态x1、x2的响应曲线.由图1(a)和图1(b)的仿真曲线可见,系统发生执行器故障F1时,状态x1、x2分别在t=2 s、t=5 s时达到渐进稳定,并且与执行器正常工作时的状态响应曲线几乎趋于一致,误差值较小. (a) 无性能指标约束时状态x1的响应曲线 (b) 无性能指标约束时状态x2的响应曲线 图2为有性能指标约束时系统发生F1故障及正常工作时状态x1、x2的响应曲线.在考虑二次型性能指标(式(4))约束的情况下,由图2的仿真曲线可见,状态x1、x2分别在t=2 s、t=3 s时达到渐进稳定,并且与执行器正常工作时的状态响应曲线 (a) 有性能指标约束时状态x1的响应曲线 (b) 有性能指标约束时状态x2的响应曲线 也几乎趋于一致,误差值较小. 综上,定理1和定理2给出的容错控制器和容错保性能控制器设计方法可以同时保证执行器有故障和无故障情况下系统的渐进稳定性,而且收敛速度较快,误差值较小,说明本文所设计的容错控制器及容错保性能控制器具有较好的容错效果. 本文同时考虑了非线性、多时滞、执行器故障及性能指标的约束等问题,针对一类具有多个状态时滞的Lipschitz非线性连续系统,设计了系统执行器发生故障时的容错控制器和容错保性能控制器.基于线性矩阵不等式方法给出了故障闭环系统渐进稳定的充分条件,并利用Lyapunov稳定性理论证明了故障闭环系统的稳定性,所设计的容错控制器和容错保性能控制器不仅可以同时保证执行器正常工作和发生故障情况下系统的渐进稳定,且收敛速度快.通过具体数值算例验证了所设计的容错控制器和容错保性能控制器具有较好的容错效果.

2 主要结果

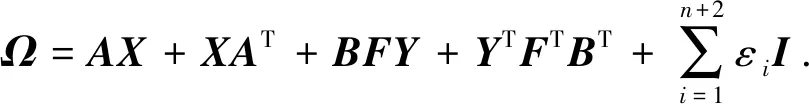
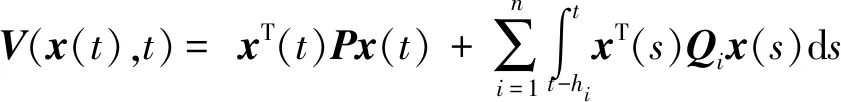

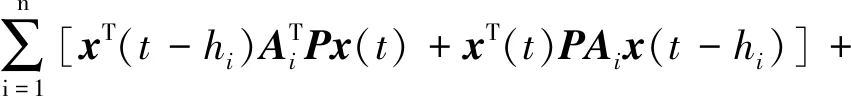
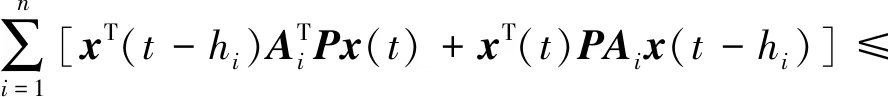


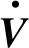
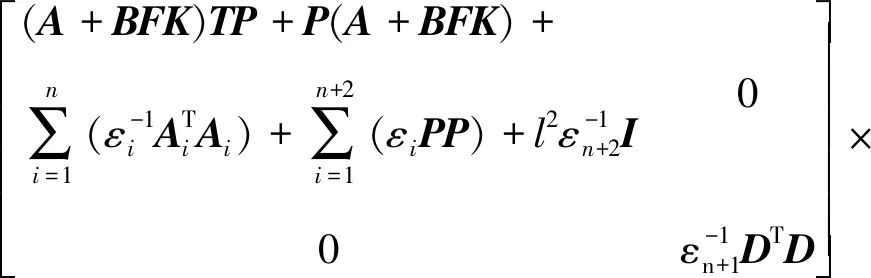

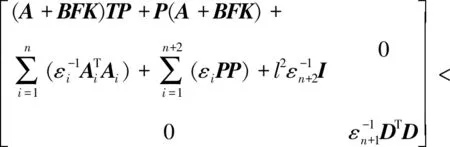


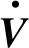

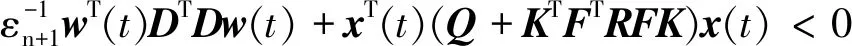
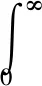

3 仿真研究
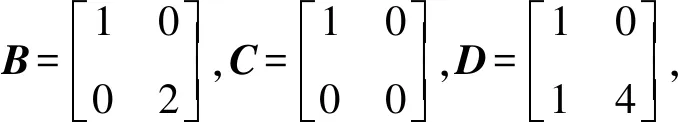

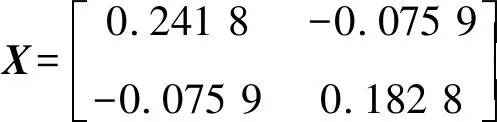
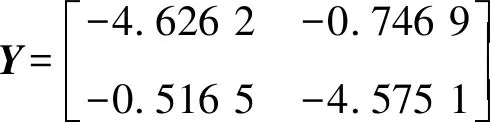

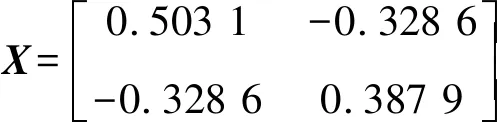



4 结语
