新型3UPS_UP并联机构工作空间及参数分析
2022-03-19李开明周文全
陈 语,李开明,周文全,张 贺
(南京理工大学机械工程学院,江苏 南京 210094)
Tricept机器人自出现以来,在飞机装配、工件加工等领域[1]很受欢迎。工作空间是并联机构的一个重要属性,一直以来也是世人钻研的热点,目前对于机械臂工作空间的求解方法主要有3种:栅格法、几何法、数值法[2]。金振林等[3]为了设计机器人步行器的腿部结构,分析了3-UPS机构的工作空间以及构件尺寸对工作空间大小的影响。曹永刚等[4]系统研究了6-RSS型并联机构并重点分析了复合球副的结构特点,通过优化机构参数使得工作空间体积得到扩大。刘震[5]采用新型数值分析法,求解出3UPU并联机构的工作空间,并应用相关算法对参数进行了优化。根据不同的结构参数,采用不同的优化策略,使结构能够达到最优化,是广大学者们研究的重点[6-8]。
本文参照Tricept机器人的结构,将动平台替换为一种复合球铰,构成新型3UPS_UP并联机构。UP杆的一侧固联在复合球铰底部,另外3个UPS杆全部由球副同复合球铰相接。由于复合球铰的特殊结构,使3个UPS杆的延长线能够汇聚于一点,而动平台3个铰点的相对位置一直变化,不便考虑动平台的姿态问题,因此以延长线汇聚点(复合球铰的球心)为动平台参考点,这样可以简化机构的运动学正反解计算。根据有关的约束条件和反解公式,运用边界搜索法可以得到该机构的边界曲面。
1 机构描述
由图1可见,3UPS_UP并联机构主要是由定平台A1A2A3、1个UP杆(L0)、复合球铰S、3个UPS杆(L1,L2,L3)构成。3个UPS杆的一端通过虎克铰布置在定平台上,另一端分别同复合球铰S的一个球副相接,铰点分别为B1,B2,B3,复合球铰半径为r。由于复合球铰S的结构特点,3个UPS杆的延长线相交于P点。UP杆的一侧固联在复合球铰S的底部,另一侧安装于定平台的重心处。该机构的自由度为3。

图1 3UPS-UP并联机构结构简图
2 复合球铰结构设计
从图2(a)可以看出,复合球铰的复合球副包括3组球副,并且3组球副的构成一致。每组球副由3个转动副组成,其中转动副1的转轴与UP支链同轴,转动副2的转轴位于同一平面,该平面通过复合球铰的球心P点且垂直于UP支链;3个UPS支链分别与球副的转动副3连接,3个转轴的延长线交汇于复合球铰的球心P。由图2(b)可知,所述复合球铰的半径为r,3个UPS杆与UP杆的夹角为θi(i=1,2,3),同复合球铰相连的UP杆直径为d。

图2 复合球铰的三维模型图及结构简图
3 位置分析
由图1可知,定平台和复合球铰上的铰点分别表示为Ai,Bi(i=1,2,3)。定参考系O-XYZ设置于该机构的定平台上,其中,原点O设置于定平台中央。定平台上3个铰点A1,A2和A3呈正三角形,它的外接圆的半径为R[9]。X轴过点A2且垂直于直线A1A3,Y轴过原点O且平行于直线A1A3,Z轴依照右手法则确定[10]。UP杆和3个UPS杆都含有移动副,其杆长分别为Li(i=0,1,2,3),移动副di(i=0,1,2,3)分别位于伸缩杆Li上。
复合球铰(动平台)上的各铰点为Bi(i=1,2,3),由于各铰点的相对位置会不断变化,因此不能像Tricept机构一样将动坐标系建立在Bi(i=1,2,3)点的几何中心。因为3个UPS的延长线总是交于一点,且该点为复合球铰的球心,所以设复合球铰中心点为P,复合球铰的球心在定坐标系中的坐标为P(x,y,z)。根据前面介绍的位置关系可得:
Li+r=OP-OAi(i=1,2,3)
(1)
式中:r为r在BiP方向的矢量。
位置反解为:
(2)
位置正解为:
(3)
4 工作空间分析
4.1 约束条件
并联机构的工作空间是指动平台参考点在空间内所有位置坐标的集合,反映了机构运动空间的大小,影响工作空间大小的主要结构因素有:
1)杆长的限制。该并联机构包含4个伸缩杆,每个伸缩杆的长度都有结构限制,必须保证参考点在伸缩杆的长度范围之内。
lmin≤li≤lmax(i=0,1,2,3)
(4)
式中:li为伸缩杆Li的长度;lmax和lmin分别为最大和最小杆长。
2)虎克铰转角的限制。
(5)
式中:φi为定平台中第i个虎克铰的当前转角;φmax为许用转角;z为基座在定坐标系中位置,z=[0,0,1]T。
3)杆件的尺寸干涉及复合球铰的限制。
由于复合球铰底部与UP支链连接,为避免极限情况下与UP支链产生干涉,因此3个UPS支链与UP支链间的夹角θi应满足:
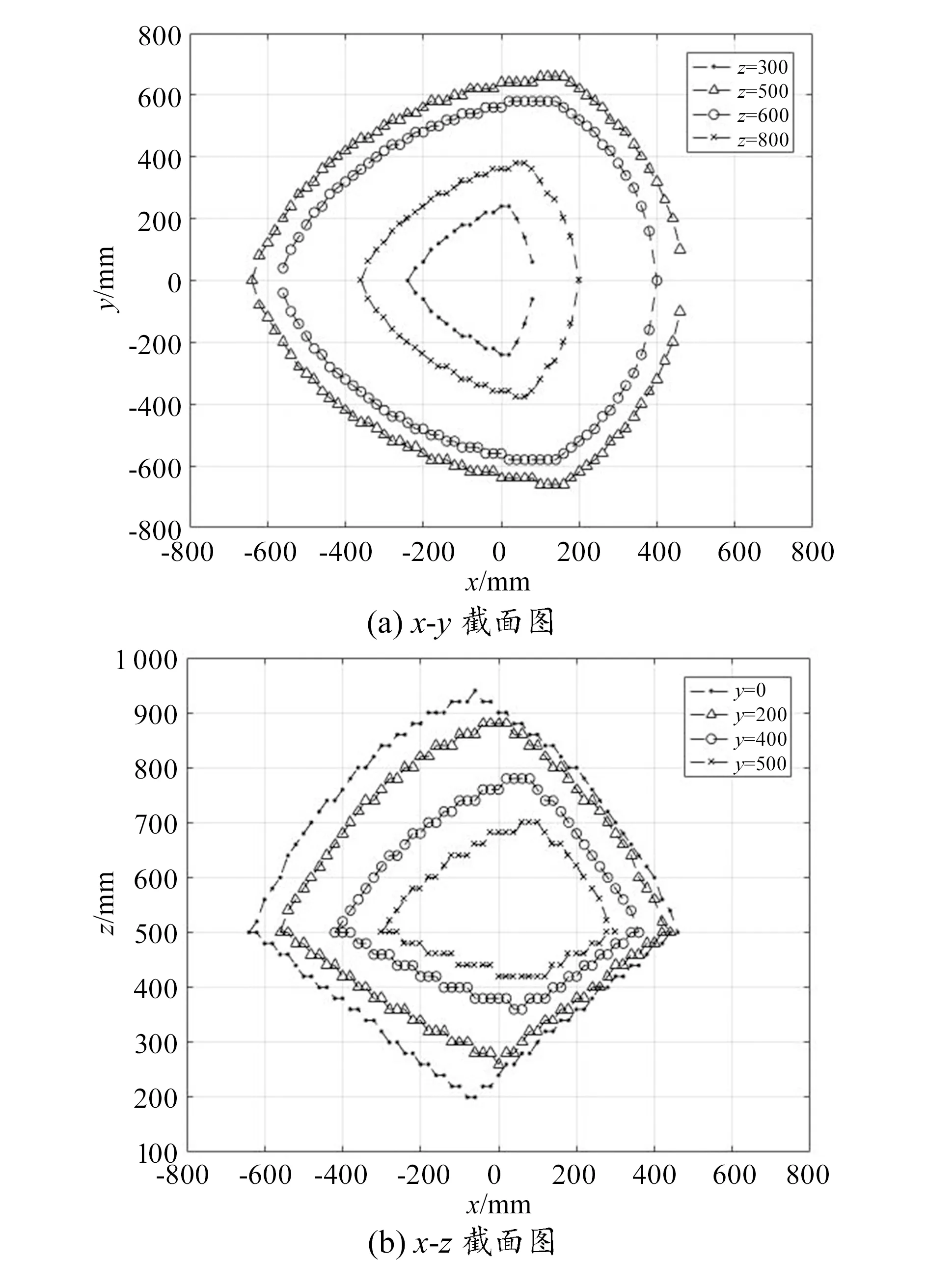
rsinθi (6) 同时,UP杆和UPS杆间的夹角也应小于θmin; (7) 本文采取边界搜索法。将动平台上参照点设为P(x,y,z)。如图3(a)所示,沿着Z轴将整个空间分为n个平行于OXY平面的微小平面,其中微小平面个数n=(zmax-zmin)/Δz,Δz为搜索步长,zmax和zmin为Z向的极限位置。如图3(b)所示,在每个平面中,极角γi从O开始搜索,在高度zi和极角γi不变的情况下,极径ρi从O开始不断增大,其增量为Δρ。当前点坐标(ρicosγi,ρicosγi,zi)是否符合要求,需要结合运动学逆解及全部约束条件来判定。在两个相邻点中,如果其中前一个点符合全部约束条件而下一个点不符合,那么前一个搜索点就为边界点。再将极角γi增大Δγ,一样可以获得γi+1的边界点,如此将平面全部搜索完成,就能够获得该平面全部的边界曲线点。在整个空间内把所有平面都搜索出边界曲线点,就可以获得该机构的边界三维图。本文采用的各方向的查找区间和增量分别为-800 mm≤x≤800 mm,-800 mm≤y≤800 mm,200 mm≤z≤1 000 mm,Δz= 20 mm,Δγ=2°, Δρ=200 mm。 图3 极坐标边界搜索法 根据上述分析方法,得到的工作空间图形如图4所示。从图可以看出,该机构的三维边界图中间部分较大,上下逐渐收缩,呈现出两头小中间大的形状。结合图4和图5(a),可见x-y截面在z=500 mm附近面积达到最大,往上下两侧面积逐渐减小,在z=300 mm和z=900 mm处,截面面积接近为0。因为3个连杆的长度和行程相同以及虎克铰安装位置关系,使得工作空间界面关于Y轴对称,此外截面形状全部相似,且具有对称性,工作空间往定平台虎克铰安装位置方向突出,所以整体形状呈120°分布。从图4和图5(b)可以看出,工作空间上下部分形状虽然有些相似,但上半部空间较大,且工作空间向连杆方向倾斜。 图4 三维边界图 图5 x-y截面图和x-z截面图 该机构中与工作空间有关的机构参数主要有支链夹角θ、定平台虎克铰外接圆半径R、UP杆直径d、虎克铰的最大转角φmax。在整体尺寸不变的情况下,只考虑lmax不变时lmin对空间体积的影响,即伸缩杆行程的影响。因为是以UPS支链交点P的运动范围作为工作空间,且复合球铰半径相对于定平台体积很小,所以忽略复合球铰半径r的影响。根据前面边界搜索法可知,在Z向上以增量Δz将整体划分为多个微小空间;对于每个微小空间,又以极角增量Δρ将其分为多个微小扇形空间,工作空间体积Vk的计算公式为: (8) 式中:ρ1i和ρ2i分别为极角γj不变时工作空间的内外边界值;Δz为微小空间的高度。整个工作空间的体积V为所有子空间的体积之和[10]: (9) 将待评价的结构参数尺寸设为变量,在MATLAB中搜寻工作空间时,在其中添加工作空间体积的计算公式。 从图6(a)中可以看出,在最大杆长lmax不变的情况下,随着伸缩杆最短杆长lmin逐渐变大,即伸缩杆行程越来越短时,工作空间的体积不断减小,开始变化缓慢,后来下降明显。由图6(b)可以看出,在其他条件不变的情况下,R对空间体积影响接近线性变化,影响比较明显;由图6(c)可以看出,虎克铰许用最大转角φmax影响也同样明显,近似呈线性变化,所以虎克铰许用转角φmax要尽可能大。支链的最小夹角θmin对空间体积同样有影响,如图6(d)所示,当θ较大时,空间体积不断减少直至为0。但由于复合球铰具有特殊结构,为了避免杆件干涉,杆件间必须要留有夹角,为了获得更大的工作空间,支链的最小夹角θmin要设计得尽可能小。 图6 结构参数对工作空间的影响 本文设计了一种以复合球铰作为动平台的新型3UPS_UP并联机构,介绍了该机构的结构及位置关系。由于复合球铰的特殊结构,简化了该机构的运动学求解。通过MATLAB分析出该机构工作空间的分布特点,并定量分析出机构的结构尺寸与工作空间之间的关系。本文的研究可为该机构结构尺寸的优化设计提供依据,有利于该机构的推广及应用。4.2 工作空间分析方法

4.3 工作空间仿真

4.4 机构参数对工作空间大小的影响

5 结束语
