一种极端自然事件下的基于深度强化学习的配电网脆弱性研究方法

周震尘， 金 涛

(福州大学电气工程与自动化学院，福建 福州 350016)

0 引 言

近年来，诸如台风、洪水及海啸等自然灾害发生的频率越来越高。电力系统在遭遇这类事件的冲击下，往往受到严重的破坏，从而造成大面积的断电[1]。近年来，中国深受自然灾害的侵扰，如2016年江苏省龙卷风灾后约13 500户家庭出现断电[2]。极端天气造成的破坏常为N-k故障，基于可靠性运行的电网在这种严重的事故下无能为力，因此，发展电力系统弹性技术，增强电网在极端事件中的运行能力十分必要[3]。

弹性电力系统能够在破坏性的外部扰动下持续向负荷供电，在扰动后能迅速恢复到正常状态[4]。根据极端自然事件发生的时间轴，可以将弹性提升的措施分为3个阶段[5]：灾前、灾中及灾后。在灾前，一般采用改变网络拓扑结构或增加元件在极端事件下的存活率来避免电网大面积停电，称之为强化措施。在此之前，必须辨认电网在灾害中最脆弱的部位，有效提升强化效果并节约强化成本。

当前，电网防御外部威胁所采用的一般方法为双层或三层（defender-attacker-defender，DAD）鲁棒优化模型[6-7]。双层优化模型的上层优化目标是通过选择破坏网络元件来最大化电网损伤，其下层目标是系统矫正上层造成的故障来最小化电网损伤[8]。三层优化模型是基于双层模型的升级版，第一阶段，防御者执行电网强化计划；第二阶段，进攻者破坏电网元件来最大化对电网的伤害；第三阶段，防御者对遭受的攻击进行紧急反应，调整潮流来最小化损失[9]。多层优化模型能够找到基于最坏情况的一个最优解，但它们仍然存在一定的缺陷[10]。一是基于模型方法的计算复杂度会随着电网规模扩大和极端事件时空特性的复杂化而急剧上升，求解时间也将成倍增加；二是当模型参数发生变化时，这类方法必须离线调整，并重新计算解决方案，这个过程过于低效。Q学习作为经典强化学习（reinforcement learning，RL）算法已经在弹性电力系统得到应用，如脆弱性分析[11]、发电调度[12]和灾后恢复[13]。深度学习（deep learning，DL）具备很强的特征提取和拟合能力[14]。2015年，结合DL的Q学习成功应用到Atari游戏中，并达到了人类专家的程度[15]，此后，DRL在许多领域得到应用[16]。弹性电网中的许多问题都能建模为MDP，从而利用DRL寻找最优策略，如发电机紧急控制[17]。

为了解决DAD模型存在的不足，本文提出了一种基于DRL的极端事件下配电网脆弱性分析方法，找到每个时刻下其故障导致的负荷削减最严重且最脆弱的线路。DRL方法相对基于模型方法的优势在于：该无模型方法有效降低了计算成本，较好地处理了随机性问题；DRL能自动学习模型变化，并制定调整策略。对电力系统的仿真验证了本文所提方法的准确性及有效性。

1 极端事件序列攻击模型

脆弱曲线能够把元件的故障率和极端事件的强度相关联，因此，通常被用于评估天气事件对电网元件的影响。脆弱曲线中，元件故障率是事件强度的函数，通过把事件强度（如台风风速）输入到模型中，能得到相应的故障率，从而将其应用到电网的脆弱性分析和极端事件的随机性模拟中。对于结构工程中的风险评估，材料脆弱性通常被模拟为对数正态累积分布函数（CDF）[18]：

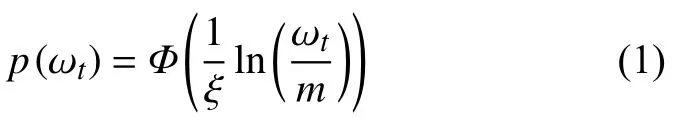
式中：ωt——t时刻下的风速，m/s；

m、ξ——工程参数中的均值、对数标准差；

Φ(·)——标准正态累积分布。

根据式（1），通用脆弱曲线描述如图1所示。

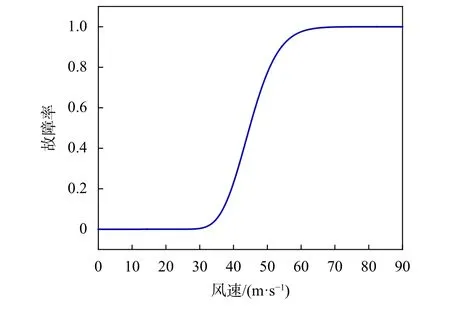
图1 与风速相关的脆弱曲线

架空线路的基本构成包括导线和杆塔，任一导线的断路和杆塔的故障都会导致整个架空线路无法工作。假设线路的每个元件故障与否相互独立，那么极端事件下架空线路的故障率为：

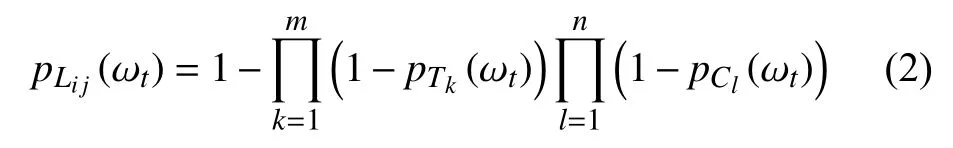
式中：pLij(ωt)——架空线ij的故障率；

m、n——架空线ij的杆塔数量、导线数量（假设相邻杆塔间有且仅有一条导线），与杆塔间距和架空线长度的比值相关；

pTk(ωt)、pCl(ωt)——架空线ij上杆塔k的故障率、导线l的故障率，用不同的均值和标准差

由式(1)计算得到。

当电网中的线路遭到破坏后，很可能在整个网络中造成连锁故障。连锁故障是电力系统弹性面临的最大威胁之一，本文主要考虑由过流引起的连锁故障，具体的连锁故障分析流程如图2所示。

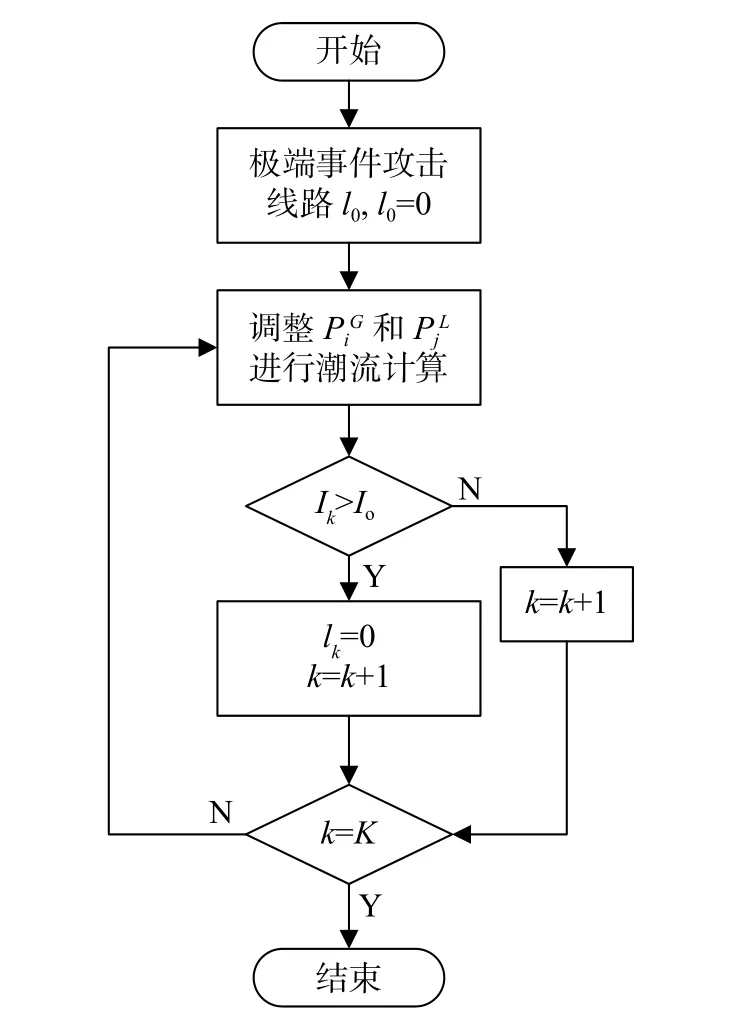
图2 连锁故障分析流程图

连续故障分析的具体流程主要分为以下5步：

1）实施攻击：当电网中的线路l0遭到破坏而发生故障时，更新电网拓扑。

3）过流检测：确认是否有任何线路电流Ik超过负载限制Io。

4）过流保护：将检测出的线路跳闸，并重新计算潮流。

5）重复步骤2）～4），对余下的K条线路进行检测，直到所有过流的线路被断开。

2 基于DRL的脆弱性分析模型

2.1 脆弱性分析模型设置

脆弱性分析站在极端事件的角度，对电网实施攻击，其目的在于破坏网络中的关键线路，从而最大化整体的损失。极端自然事件对电网的影响具有随机性，是分析中必须考虑的因素，在成本有限的情况下，对在事件压力下最可能发生故障的元件进行加固是最为可行的办法，本文以最大化负荷削减值（load shedding，LS）为目标函数：

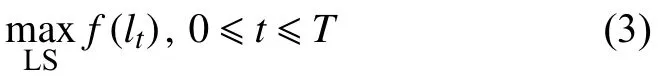
其中lt为t时刻受极端事件影响的线路。

对于式（3），其t时刻处于状态St下的功率平衡约束为：

目标函数约束发电机有功及无功输出限额及负荷有功功率及无功功率限制如下式所示：

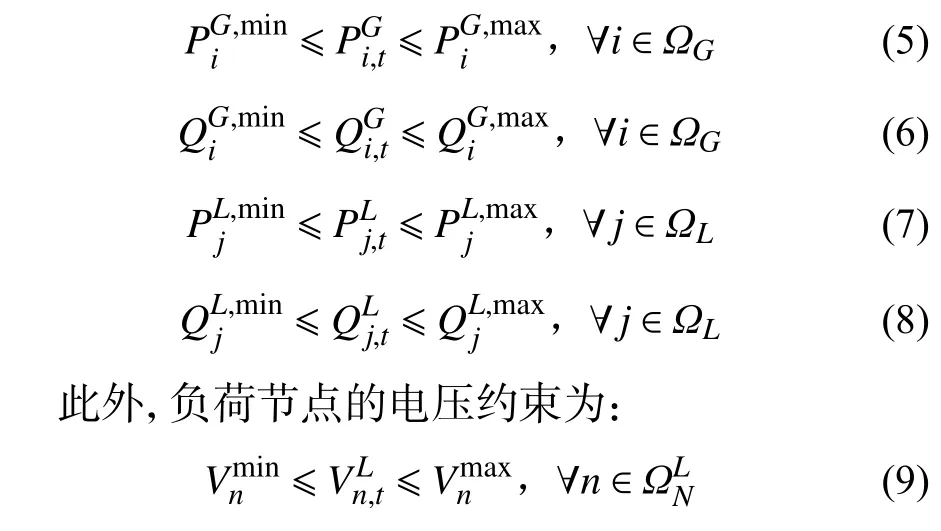
2.2 基于深度强化学习的脆弱性分析算法

强化学习是智能体通过与环境的不断交互，获取信息来不断改善自身决策能力的过程。通过折扣因子 γ将当前状态st下采取动作at得到的回报r(st,at)序列累加可以形成累积回报，那么，智能体的目标就是最大化这个累积回报：

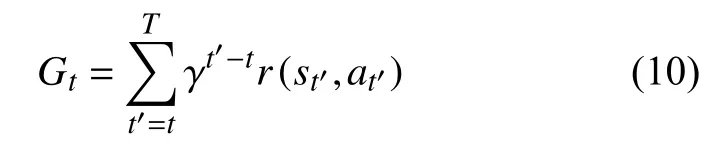
深度强化学习中最广为人知的一类算法是深度Q网络（deep Q network,DQN）。固定目标Q值要求DQN拥有两个神经网络：估计网络和目标网络，估计网络用于评估策略，其网络参数不断更新；目标网络用于产生目标值，其参数不进行更新，从估计网络直接复制参数，提高算法的稳定性。

智能体将每个时刻的数据et=(st,at,rt,st+1)存储到经验池Dt={e1,···,et}中，达到一定数量后从中随机抽取部分数据Dupdate∈Dt作为估计网络的输入对网络参数 θi进行更新，从而打破了状态间的相关性。其损失函数定义为：

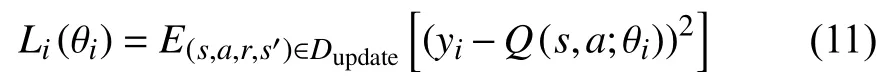
利用随机梯度下降对该函数进行更新：

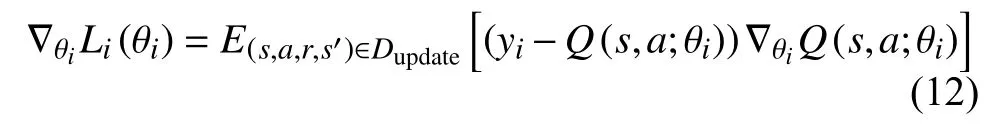
上式中的yi与智能体是否处于回合结束的状态有关，如下：

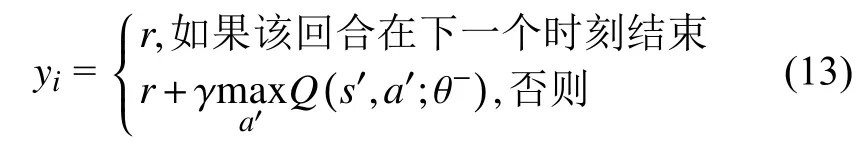
DQN的目标Q值都是通过贪婪法得到的，即智能体每次都选取Q值最大的动作，因此该算法很容易发生过估计，导致最终结果出现较大的误差。本文提出了Double DQN（DDQN），通过解耦动作选择和目标Q值计算来消除过估计，并且在一定程度上提升了收敛速度。本文假设极端事件仅对电网中的配电线路造成影响，某时刻的初始攻击和随后可能发生的连锁故障都会导致线路无法工作。因此，假设网络共有n条线路，那么时刻t下智能体所处状态可以表示为：

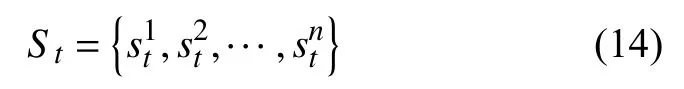
在脆弱性分析中，智能体扮演攻击者的身份，寻找对电网造成最大破坏的攻击序列，因此其动作是对网络中任意k条线路的攻击。若t时刻动作at=l，那么线路l被断开，状态

本文应对的极端事件具有随机性，在脆弱性分析中不仅要考虑线路故障对系统造成的影响，同时也要考虑线路在事件中发生故障的可能性，回报需要将LS和线路故障率按比例加和以做双目标优化：

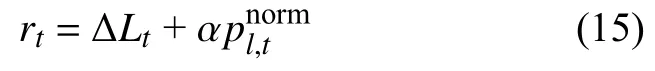
ΔLt——t时刻的LS，如式（17）所示。

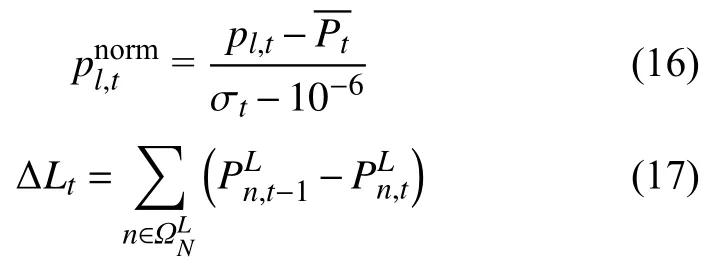
脆弱性分析的算法总体流程如图3所示，总训练回合数是it，每个回合包含te个时刻，经验池总样本量为nm。在对整个训练过程和电网状态st进行初始化后，智能体基于当前状态采取攻击动作at，随后利用连锁故障模型对此次攻击附带的线路故障进行判定，从而产生回报信号rt和新状态st+1，并将包含{st，at，rt，st+1}的经验放入经验池。当样本量足够，即n=nm时，对神经网络进行训练。最终，i=it时，结束该流程。

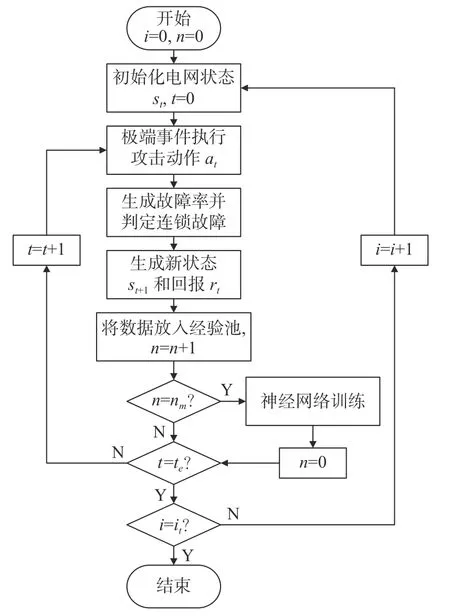
图3 提出的脆弱性分析算法总流程图

3 仿真分析及讨论

本文利用IEEE37节点系统对所提出的框架进行仿真验证和分析。仿真中假设极端天气事件是台风，其对电网造成影响的时空特性通过多阶段、多空间的建模实现。IEEE37节点系统拓扑如图4所示。

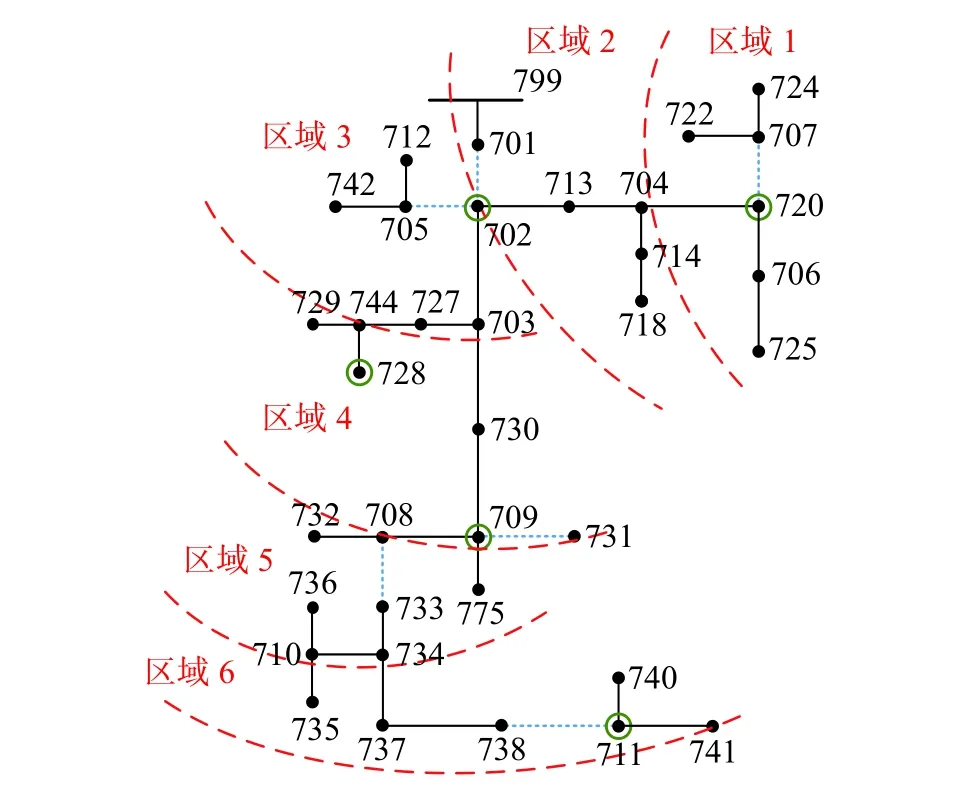
图4 IEEE37节点系统及台风路径

如图4所示，该节点系统中共有5台分布式发电机（distributed generator,DG），其所处节点位置及输出功率如表1所示。

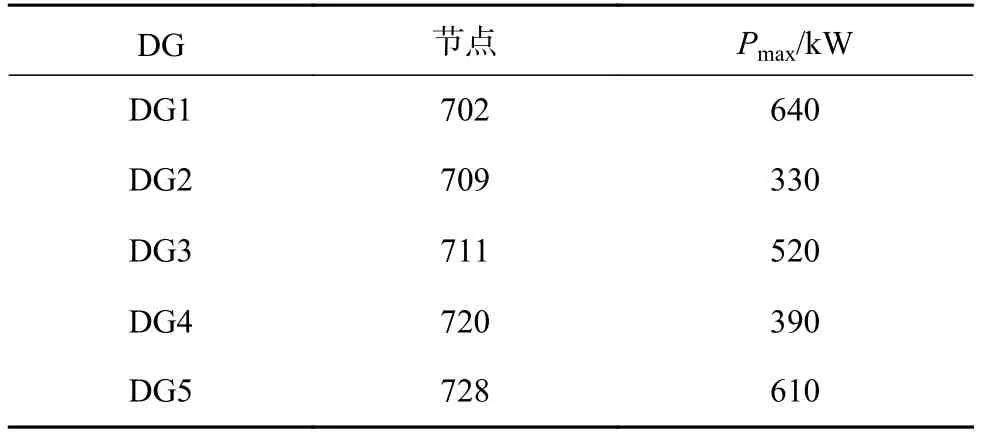
表1 DG参数

同时，IEEE 37节点系统具有25个负荷，这些负荷的节点位置及参数如表2所示。

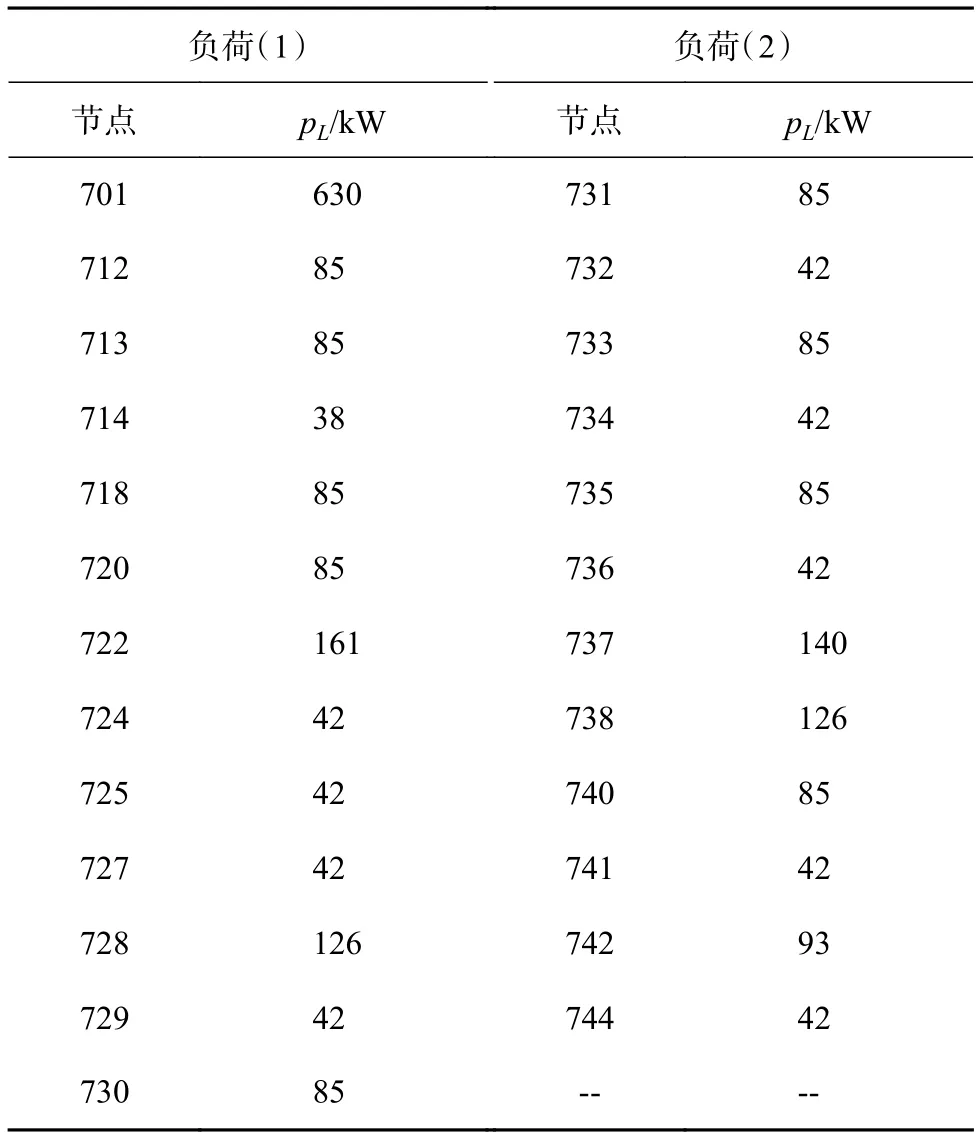
表2 负荷参数

图5是本文提出的DDQN算法和DQN法百回合平均累积回报的变化过程。可以看出DQN在前2 720回合的学习效果较快，随后逐渐稳定，并在10 270回合收敛于1 430.71。而DDQN前期累积回报的快速上升阶段仅持续到2 500回合，最后在9 600回合达到和DQN相同的最优值。从表3中收敛回合和时间可以看出DDQN的寻优速度更快，收敛前2 000回合的标准差表明DDQN在寻优过程中的稳定性也强于DQN。

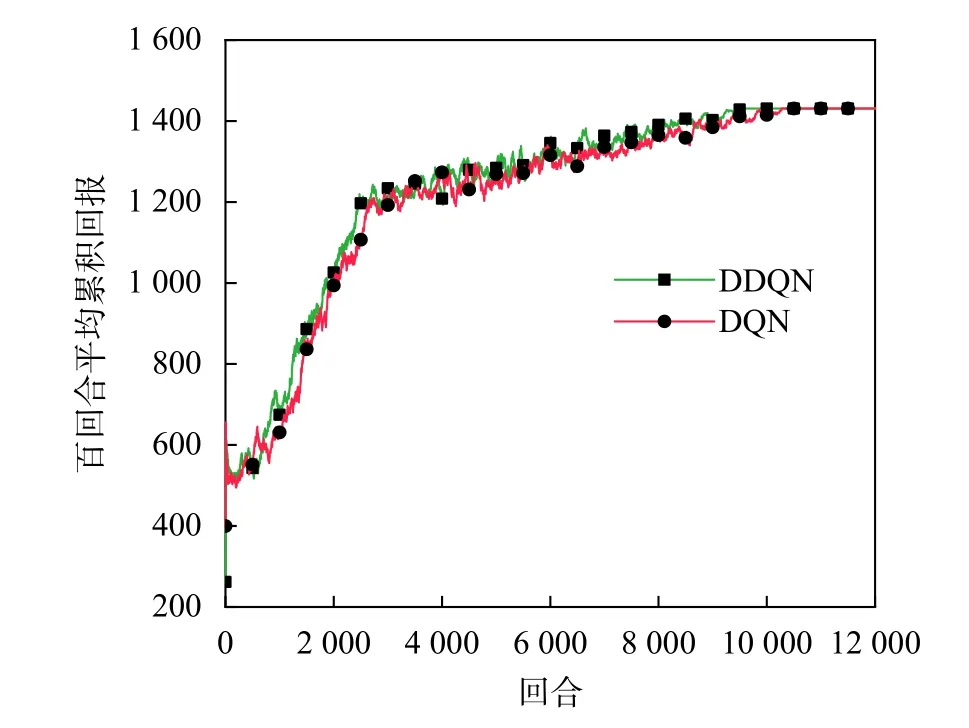
图5 百回合平均累积回报变化过程

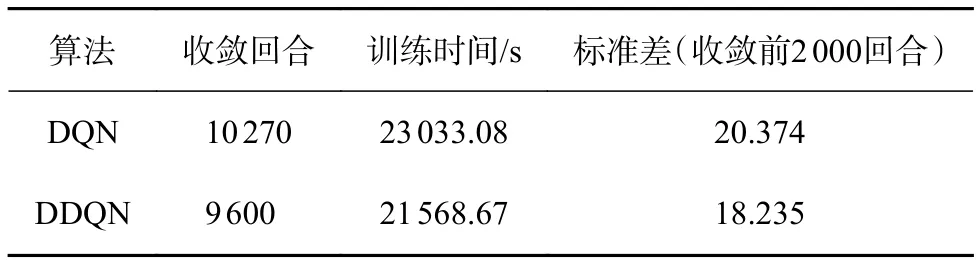
表3 训练效果对比

每个时刻的回报由智能体所选择线路的断线后系统的LS和该线路的标准化故障率构成，图6和图7分别显示了这两个回报信号各自的训练过程。从图6中可以看出，系统的LS在波动上升后收敛到最大值1 386 kW。

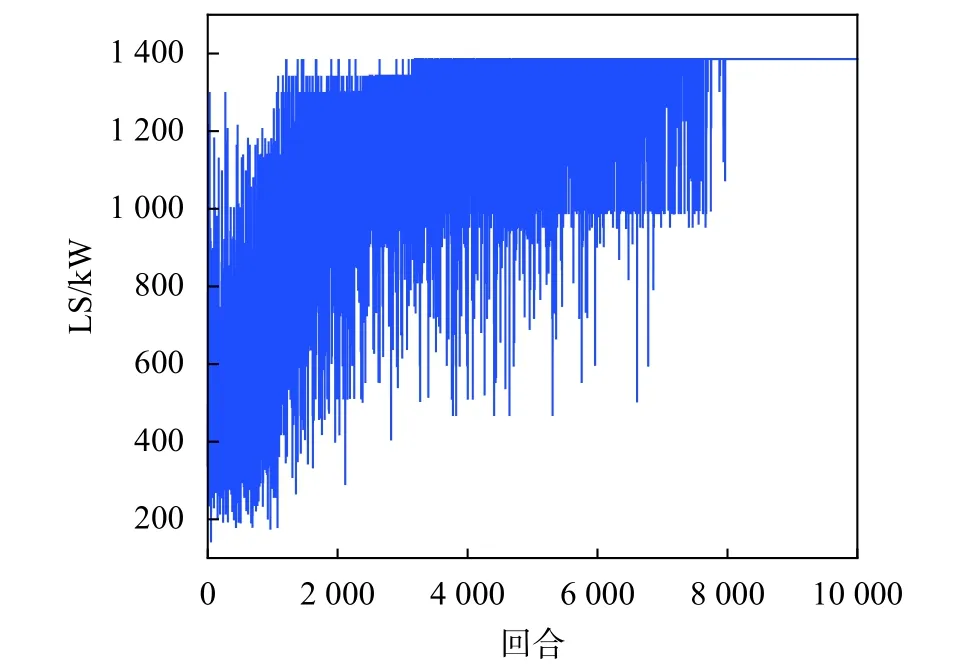
图6 LS变化过程

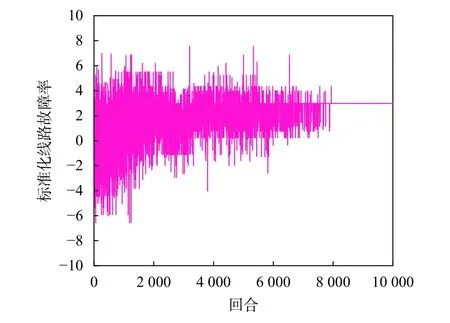
图7 线路故障率变化过程

而图7中标准化线路故障率训练后来到局部最优值2.980，这是双目标优化所导致的一个折中结果，即线路故障率在回报中权重占比较小。

本文假设每个区域内受影响的线路只有一条，智能体最终确认的关键线路序列及其故障导致的系统LS如表4所示，关键线路在图4中用蓝色虚线标明。

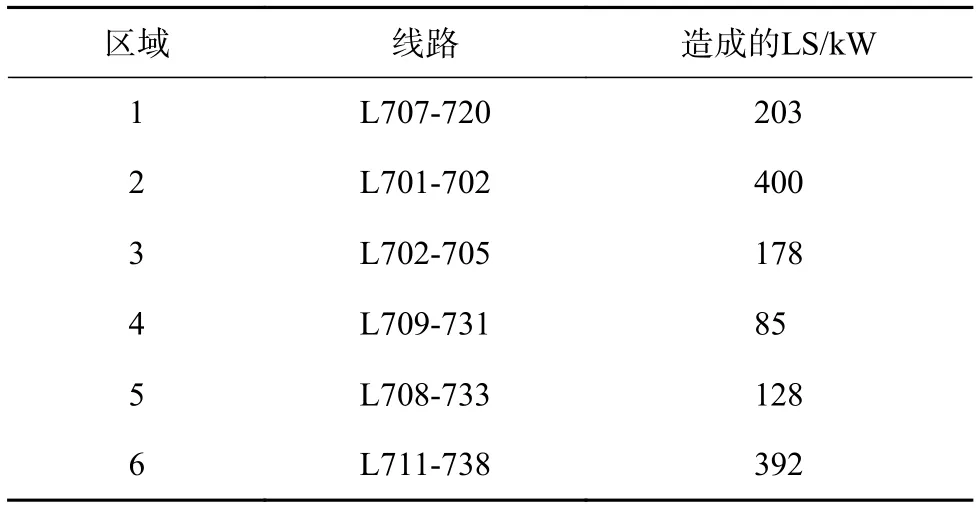
表4 关键线路序列及其故障造成的LS

图8显示了受到攻击的6条线路在一个回合内的线路电流变化过程，可以看出，当线路在某个时刻被攻击发生断线时，流过该线路的电流直接下降到0。

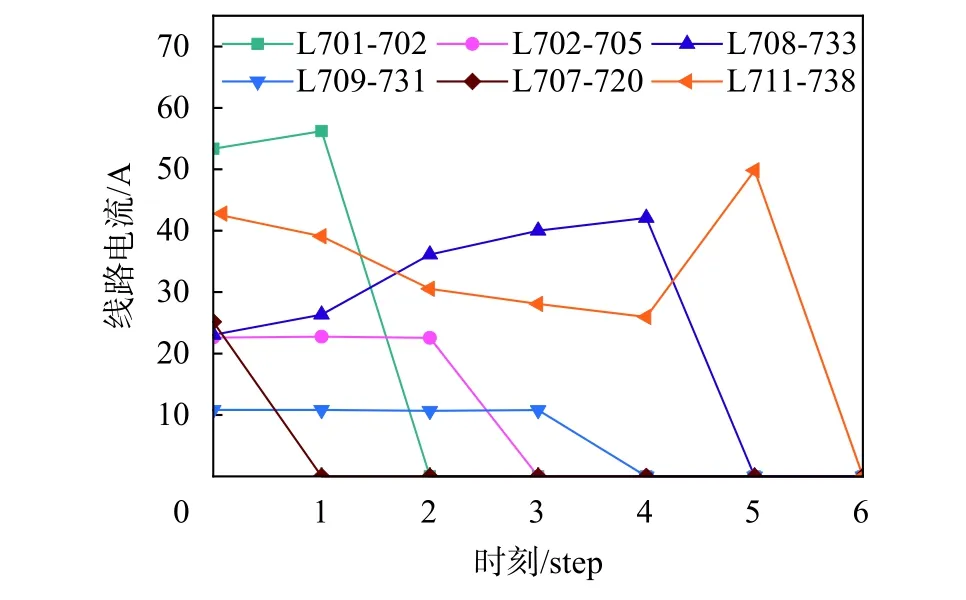
图8 受极端事件影响线路电流变化

系统总负荷在一个回合内的变化过程如图9所示，表明了系统在极端事件最优线路攻击的影响下，负荷水平出现了很大的下降。在首次攻击开始前，系统总负荷为2 457 kW，经过6次不同线路的断线故障后，系统总负荷下降为1 070.61 kW。

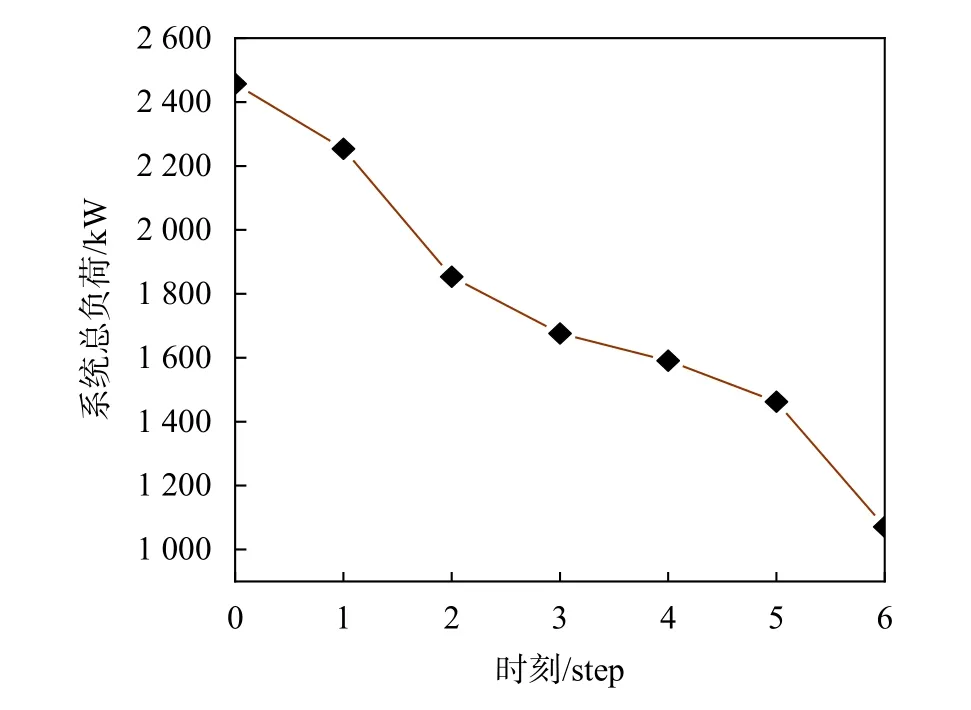
图9 系统总负荷变化

从图8和图9可以看出，通过DDQN确认的最优攻击序列有效地将工作中的线路转变为断线状态，并成功引发了系统大程度的负荷削减。

4 结束语

本文通过MDP对极端事件序列攻击建模，并结合了元件故障的随机性，考虑了受灾害影响的线路可能导致的过流连锁故障，提出了一种基于DRL的配电网脆弱性分析方法。仿真结果研究表明，本文所用方法在经过短时间的训练后，能够有效地找到每个区域内的关键线路，这些关键线路的故障将导致配电系统发生最大程度的负荷削减，并且，它们在灾害发生过程中有较高的故障率。在将来的研究中，可以进一步改进DRL算法，提高收敛速度；同时，能够对每个时刻发生的故障进行更深入的分析。