基于点云的高精度螺纹锥度测量方法
2022-03-19尤睿琦
尤睿琦, 张 超, 郝 刚
(天津理工大学计算机科学与工程学院,天津 300384)
0 引 言
随着航空航天、交通等领域高端装备制造技术的飞速发展,高性能工件的加工制造面临许多新的挑战[1]。高精度螺纹作为高性能精密工件之一被广泛应用于多种领域中,其参数的准确测量对生产应用有重要意义。其中螺纹接头因密封性、连接度、抗腐蚀等多方面的不同要求需要确保极高的检测精度与检测效率。螺纹锥度是螺纹接头较为重要的一个参数,制造精度直接影响特殊螺纹的连接强度与旋合性。如果误差超出设计精度将导致密封面接触应力减少致使螺纹接头泄漏风险增大[2]。因此对螺纹锥度进行高精度测量十分必要。
在螺纹检测过程中,人们多采用二维图像、三坐标测量机等测量方法。但这些方法在实际应用中存在测量位置单一,维护成本高,对测量环境要求严苛等问题。而非接触式点云采集技术与测量技术的研究发展在一定程度上对上述问题的解决有所帮助。因此,三维点云在工业检验中的应用场景日渐增多[3-4]。
He F等[5]提出了一种结合光学技术和图像处理技术测量油管螺纹的物理尺寸的方法并进行了进一步分析。Min J[6]使用CCD获得螺纹基本图像,最终讨论了利用机器视觉测量螺纹齿角参数的方法。Tong等[7]使用位置敏感装置(PSD)测量螺纹轮廓的坐标数据,并通过高精度栅格测量精密工作台的轴向位移对螺纹轮廓进行检测和估计。Gadelmawla等[8]基于以上研究建立了一种用于自动检测大多数类型螺纹的视觉系统。Chen Manlong[9]确认在通过投影图像测量螺纹时始终存在螺纹轮廓畸变现象并推导了螺纹轮廓变形的公式,最终给出了相应的补偿算法。Min[10]等采用了机器视觉和光学放大技术来测量高精度的螺纹几何误差,提出了一种使用改进的Sobel算子获得图像边缘的新方法,其误差小于10 μm。Li Z等[11]提出了一种基于ResUnet和隐马尔可夫模型(HMM)的外螺纹测量方法,误差同样在10 μm之内。左建中[12]与包能胜[13]分别通过Hough算法及Harris 角点检测算法对二值图像进行处理得到各项高精度测量结果。以上研究使用二维图像对螺纹各项参数的检测精度均已达到较为理想的情况,但二维图像的局限性导致了单次采集数据时仅能得到单个角度的测量数据。在数据采集过程中二维图像的获取对环境要求也相对较高。
Kosarevsky等[14]从剖面测量机获得的2D点云中通过Hough变换自动提取螺纹的特征参数。Sebastian等[15]提出一种整体方法将复杂螺纹几何形状参数化并确定区域测量策略,并通过数值模拟确定测量不确定性。张建兵等[16]建立了交点与螺纹中径线的数学模型,推导出了中径和螺距的计算公式。为未知理论螺距和牙型角的螺纹测量提供了新方法。王洋洋[17]基于张建兵的工作利用测点数据结合逆向建模对建模后的螺纹参数进行检测。目前三坐标测量机多用于包括石油套管等精密螺纹的检测,其误差可达5 μm以内。但三坐标测量机体型笨重,造价昂贵且保养困难。多数测量机采用接触式检测法且在使用前需将待测螺纹固定在水平面上。这也导致了无法做到实时检查和全面检查。
Robertson C等[18]通过遗传算法及预先建立的螺纹双曲线模型从结构光点云数据中测量出螺纹大小径。但该方法需要已知螺纹部分参数且测量精度不理想。谢张宁等[19]通过对螺纹点云求取快速凸包并通过最小二乘法拟合得出螺纹点云的中轴线最终验证了该方法相较于传统投影法的优越性。
本文通过非接触式三维结构光扫描仪得到外螺纹点云并对其摆正及分割工作进行了探讨,提出对分割后的数据按轮廓连续性分别进行聚类以提取锥度特征点,在聚类结果与锥度拟合点之间建立了数学模型,并提出了一种自动计算螺纹锥度的方法。
1 测量流程及重点方法
在实地应用中受场地扬尘及待测螺纹表面反光影响会产生大量噪点最终影响测量结果。本文的目的是通过对点云的处理与研究令噪点对测量结果影响最小化,从而做到高精度的螺纹锥度测量。基于原始数据的复杂性及采集位置受到的限制,本文对不同角度获取的含端面螺纹数据进行分类讨论。首先使用基于端面轮廓的摆正方法统一对数据进行摆正,之后根据不同采集角度得到的数据提取为对应轮廓断续点云与轮廓连续点云后分别应用对应方法进行聚类。得到聚类结果后,使用提出的特征点寻找模型得出特征点集。最后对特征点集进行拟合得到待测螺纹的锥度线。整体流程如图1所示。
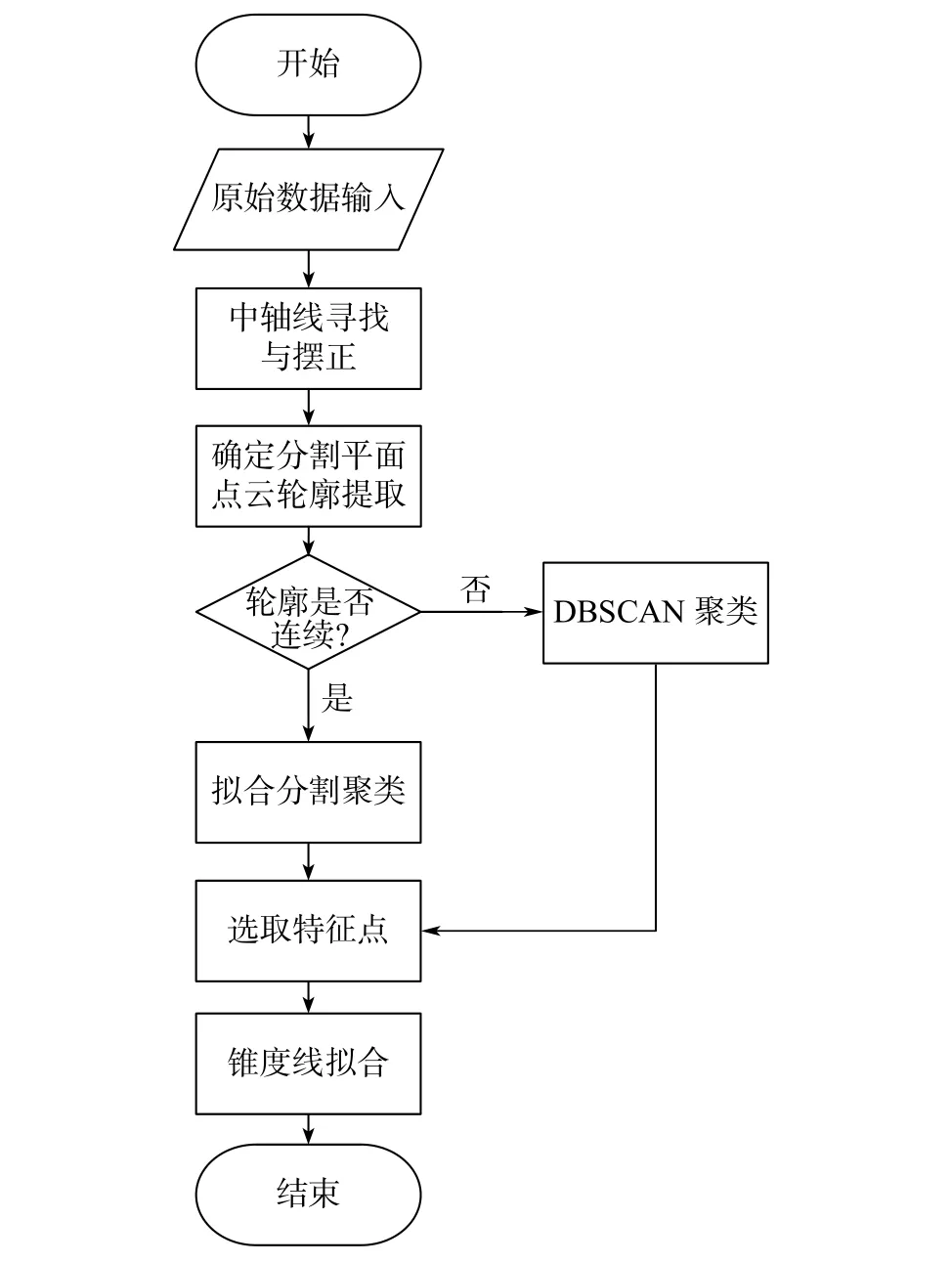
图1 测量流程图
本文在无需夹具的情况下对多种螺纹进行了锥度测量,轮廓断续点云平均锥度测量误差为0.05°,轮廓连续点云平均锥度测量误差为0.02°。在整个过程中,重点步骤如下:
1)含端面数据的局部螺纹点云摆正。由于在数据采集过程中点云扫描仪会因为工业环境产生的震动发生细微偏移。考虑到测量时无法使用夹具固定待测工件,需要一种方法对不同位置的点云进行摆正以便测量。本文通过确保扫描仪位置获得部分或全部端面数据后通过基于端面的摆正方法进行摆正。在摆正过程中使用拉依达准则降低噪点对摆正的影响。
2)点云轮廓聚类。在通过摆正与分割得到对应轮廓后,需要对不同情况进行分类讨论。对于在端面一侧采集得到的轮廓断续点云和在螺纹一侧采集得到的轮廓连续点云,本文分别使用DBSCAN聚类算法与本文提出的拟合分割聚类对待测数据进行聚类。最终得到便于特征点提取的点云集合。
3)特征点提取。对轮廓点云进行聚类后,通过数学模型提取每一类中锥度特征点,减少噪点以达到提升精度的目的。对得到的特征点进行拟合即可得到最终测量结果。
2 重点算法实现过程
2.1 数据预处理
2.1.1 点云摆正
谢张宁[19]通过随机增量法构成凸包点集后使用最小二乘实现对螺纹点云中轴线的高精度提取,这种方法对于局部螺纹点云与特殊螺纹点云而言难以构建形状合适的点云凸包,从而导致中轴线获取难度较大。为解决这一问题,提出基于端面轮廓的点云摆正方法如下:
1)原始螺纹点云A,使用快速k近邻提取点云轮廓并分析得到端面点集i。
2)使用随机抽样一致算法(RANSAC)对i进行平面拟合并通过拉依达(3σ)准则滤除端面点集i中噪点提升平面拟合精度及端面点集信噪比。最终得到平面l。
3)计算得出平面l与平面xoy的旋转矩阵R1,将A乘以旋转矩阵R1进行坐标变换成为A′,同理将端面数据i变化为i′。
4)对i′进行椭圆拟合得到圆心并计算与坐标原点的变换矩阵R2,将A′乘以R2即可变换为中轴线为z轴的摆正点云A′′。
变换后获得点云如图2所示。
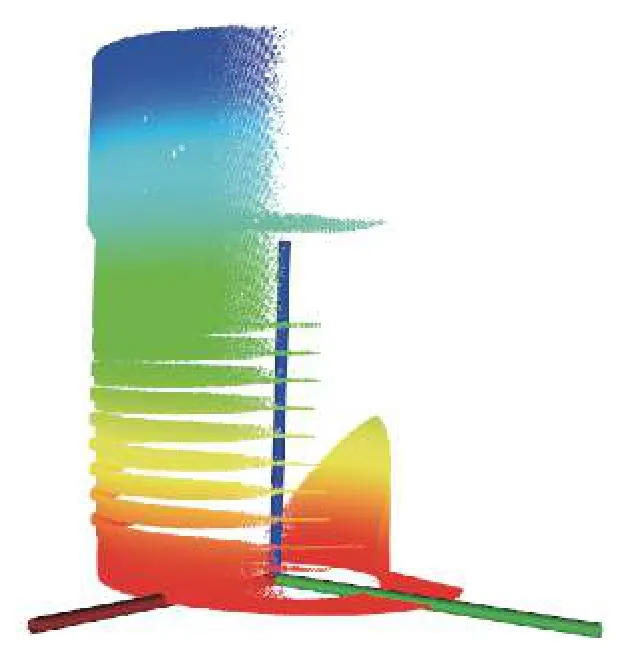
图2 摆正后的轮廓断续点云数据
2.1.2 确定分割平面
众所周知,过不在同一直线上的三点有且只有一个平面,定量且有序的找到这三个点即可定义一个合理的空间平面。关键步骤如下:
1)使用圆的参数方程x=Rycosθ=Rsinθ,其中θ∈ [0,2π)定义圆心在空间坐标原点的正圆点云O。
2)取O的圆心坐标为p1,取z轴方向上的任意点作为p2。
3)对O上依次取点作为p3即可获得沿z轴旋转的平面。
已知三点p1(x1,y1,z1),p2(x2,y2,z2),p3(x3,y3,z3)作向量p1p2(x2–x1,y2–y1,z2–z1),p1p3(x3–x1,y3–y1,z3–z1),平面法线和这两个向量垂直,因此法向量n:
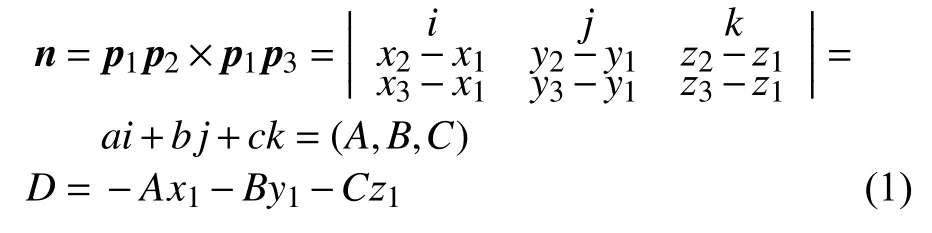
上式解出A,B,C,D即可得到平面p的一般式方程为Ax+By+Cz+D=0。
整体分割方法如图3所示。
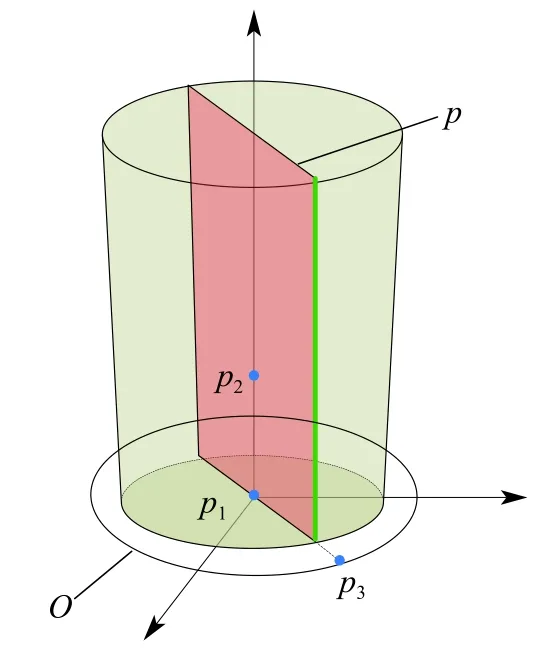
图3 分割平面选取示意图
2.1.3 获取螺纹点云轮廓
2.1.2节中得到了以z轴 为旋转轴的分割平面。接下来通过遍历点云中所有点并计算其到分割平面的距离。选取距离小于阈值的点组成轮廓点云。
任取平面内一点P(x,y,z)连接PQ,过P做平面的法向量n=(A,B,C)。可知Q到平面距离d恰是PQ在法向量上的投影长度,如图4所示。
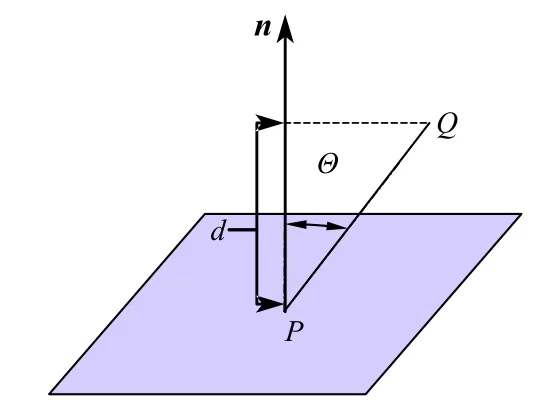
图4 轮廓提取示意图
点云离散点Q到分割平面的距离d的计算方法如下:
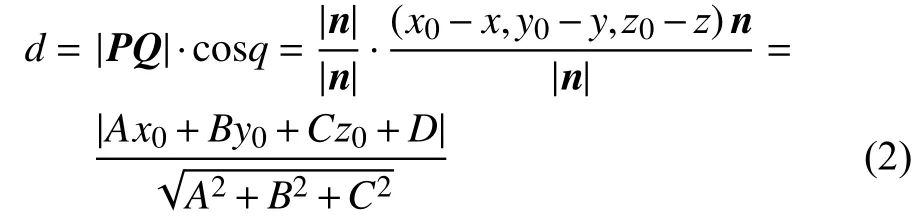
对得到的所有分割平面进行点云轮廓提取。得到点云轮廓后使用如下方法对点云进行二维映射:

对得到的二维点集进行聚类用于分离螺纹顶部与底部数据。
2.2 点云聚类
2.2.1 DBSCAN聚类
在 DBSCAN(density-based spatial clustering of applications with noise)聚类算法中,聚类精度对邻域阈值(Eps)和点数阈值(Minpts)取值敏感,人工选取严重影响测量自动化与算法鲁棒性,同时可能造成聚类不准确等问题,为此已有不少文献提出若干参数自适应方法。本文参照文献[20]使用的自适应参数方法,根据待测数据自身特性以及可视化展示,为算法确定合适的参数。
图5展示了轮廓断续点云的聚类过程。其中,图5(a)表示了轮廓断续点云因受制于检测位置获得的点云轮廓。图5(b)表示了经过DBSCAN聚类获得的第3类点云点集。

图5 DBSCAN聚类
2.2.2 拟合分割聚类
轮廓连续点云的数据受扫描角度影响,单个轮廓中含有更多螺纹信息。但同时因为数据点均匀且连续,无法使用基于密度的聚类方法。基于以上原因,本文提出一种通过拟合分割进行聚类的方法如下所示:
1)读入点云轮廓S,通过曲率分析去除端面数据与管面无螺纹数据。得到待聚类数据S′见图6(a)。
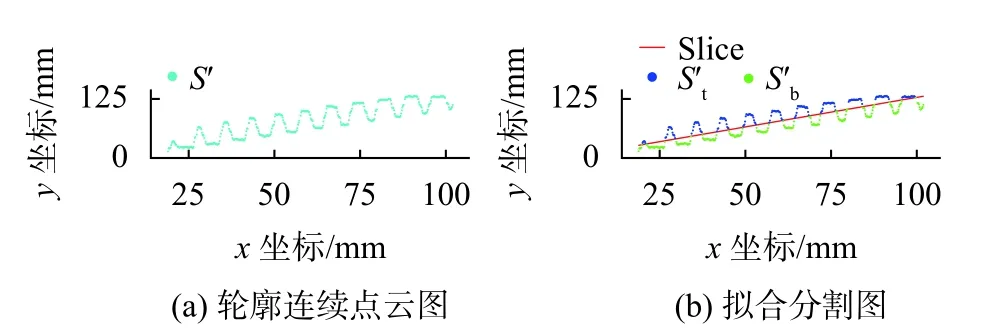
图6 拟合分割过程图
2)对S′进行拟合得到粗分割线Slice,并以此将待聚类数据S′粗略分割为顶部数据与底部数据如图 6(b)所示。
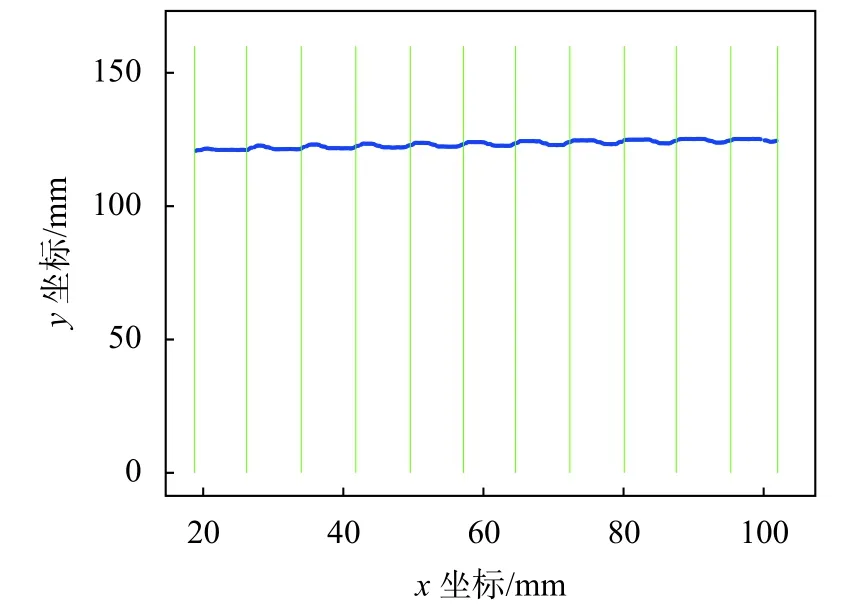
图7 聚类分割示意图
4)按聚类分割线对点云轮廓S按x值进行分割即可得到聚类后点集Si(1<i<n)。其中聚类数目为绿线数目减1。
2.3 特征点选取及数据拟合
2.3.1 特征点选取模型建立
通过对聚类数据的结构分析及具体实验,考虑锥度测量的特征点位置以及噪点的影响提出特征点选取模型如下:
提取顶部特征点:
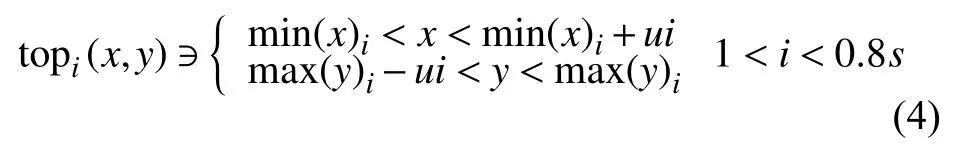
提取底部特征点:
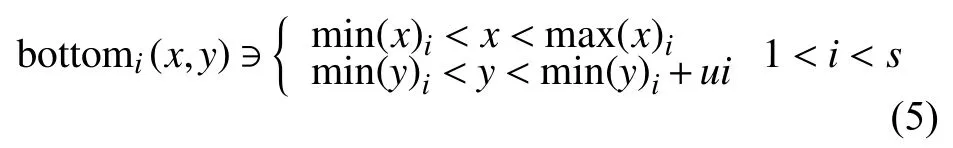
式中:m in(x)i——第i类x最小值;
topi(x,y)——顶部第i类特征点;
bottomi(x,y)—底部第i类特征点;
u——修改系数;
s——总类数。
将各点集取并得到数据拟合点集如下式:
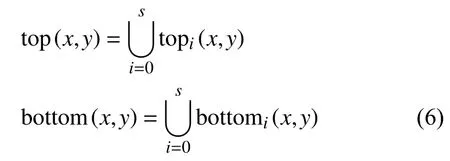
2.3.2 数据拟合
使用直接最小二乘法分别对最终得到的顶部特征点集top(x,y)与底部特征点集bottom(x,y)进行直线拟合,得到各自的斜率kt与kb。结合顶底特征点数numt,numb由下式可得最终测量结果k:
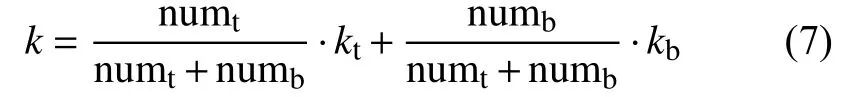
3 测量结果分析
本文算法在Windows10操作系统中使用VS2019及QT5.14.1实现,使用的开源库分别为PCL、OpenCV等。分别对DBSCAN聚类的轮廓断续点云和使用拟合分割聚类的轮廓连续点云进行了实验。
3.1 实验数据来源
实验数据来源于天津微深科技有限公司VTOP650T非接触式蓝光拍照式三维扫描设备系统于实际生产环境中实地扫描得到的点云数据。其中各螺纹锥度制造公差范围均为2.57°~2.7°。
3.2 误差定义
本文使用累计平方误差与平均绝对误差来评估提出算法的测量准确度。函数分别定义如下:
累计平方误差函数
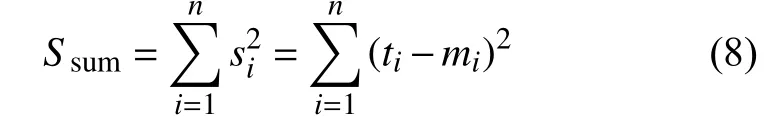
平均绝对误差函数
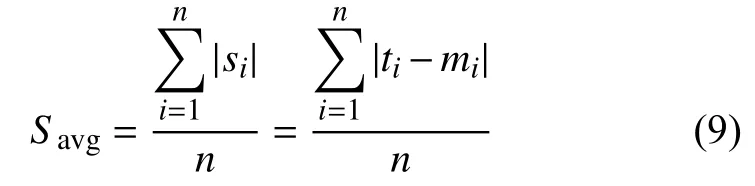
式中:ti——第i个样本的实际值;
mi——该样本通过本文算法得出的测量值;
si——该样本测量误差
n——样本总量。
3.3 结果分析
由于受采集角度限制,轮廓断续点云信噪比通常较低。轮廓的不完整性对聚类结果及特征点数量均产生较大影响从而导致检测结果不佳。本文的螺纹锥度测量方法对以上情况具有一定的鲁棒性。表1为10组轮廓断续点云通过DBSCAN聚类的测量结果,图8为对应误差比较图。
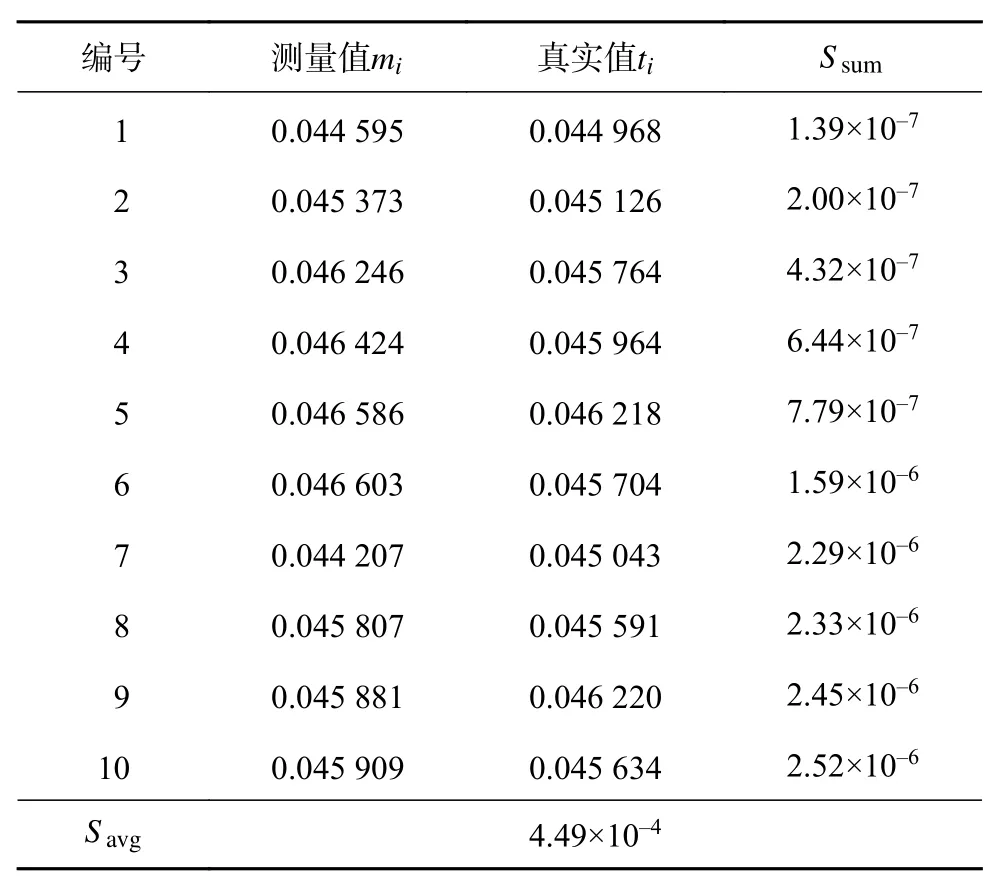
表1 轮廓断续点云测量结果
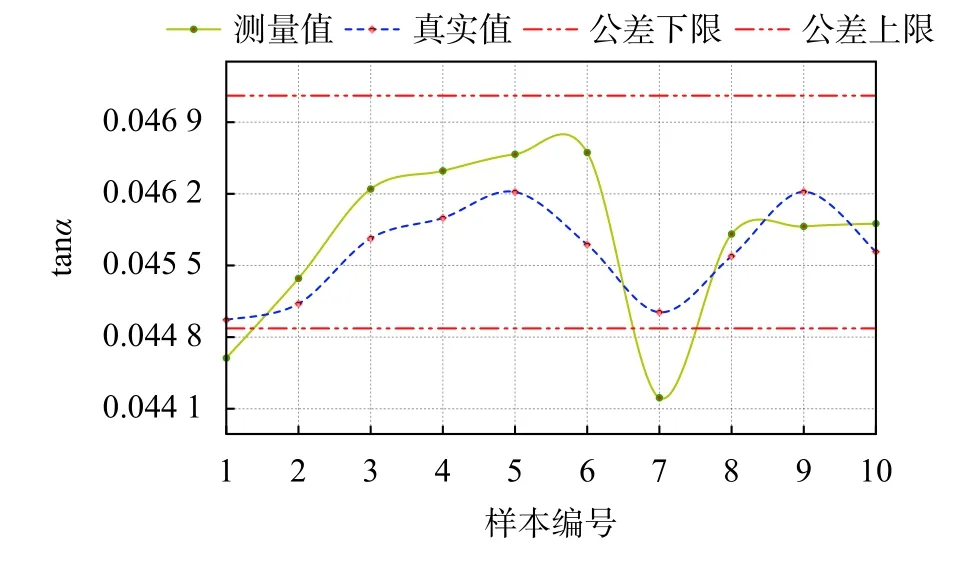
图8 轮廓断续样本测量误差比较图
由图8的对比结果显示,轮廓断续点云测量方法对噪声具有较好鲁棒性,但仍有部分测量结果偏差较大。其中1、7号样本因误差出现工件实际质量合格测量结果不合格的情况。锥度平均绝对误差为 arctan(4.49×10–4)×2=0.05°。
表2显示了使用轮廓连续点云测量方法的测量结果。使用拟合分割进行聚类的轮廓连续点云得到的聚类数量与聚类精度均高于轮廓断续点云,所以测得精度较高。最终锥度平均绝对误差为arctan(1.91×10–4)×2=0.02°。图 9 为误差比较图。通过对比轮廓断续点云与轮廓连续点云的累计平方误差变化情况,可以明确看出使用轮廓连续点云测量法最终测得结果显著优于轮廓断续点云测量方法,如图10所示。
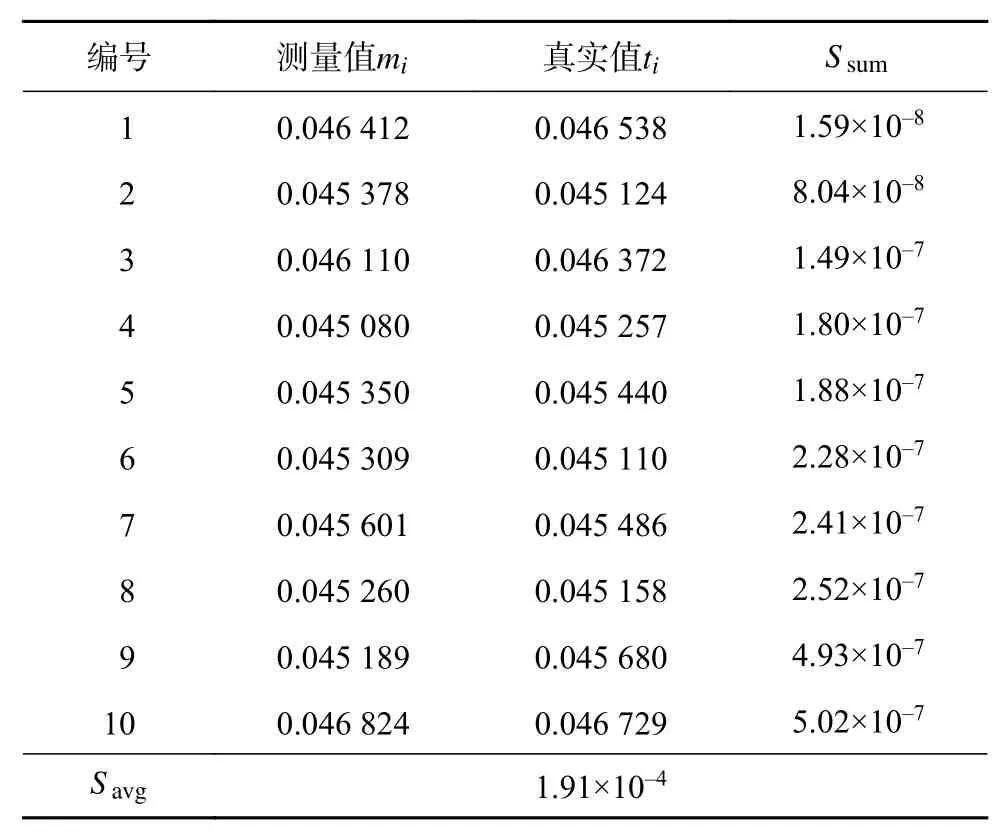
表2 轮廓连续点云测量结果
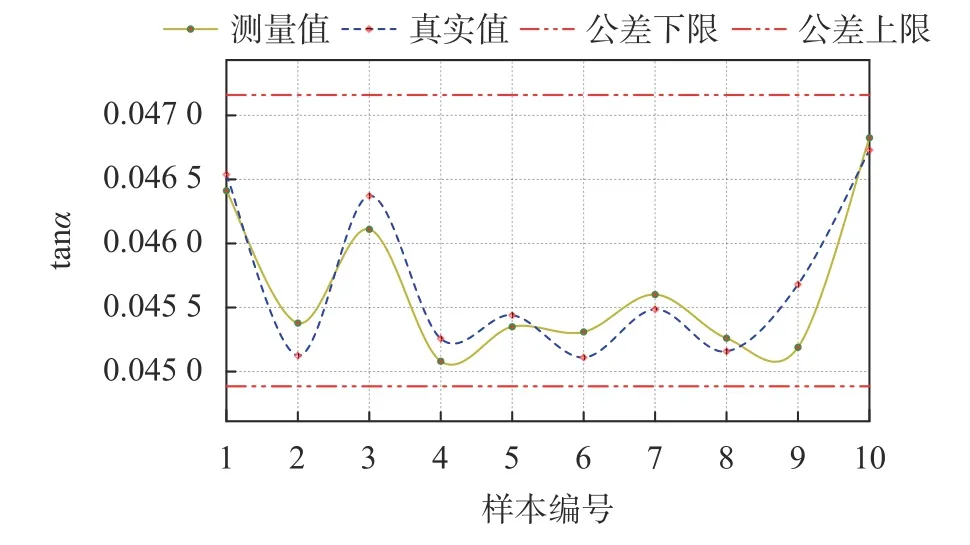
图9 轮廓连续样本测量误差比较图
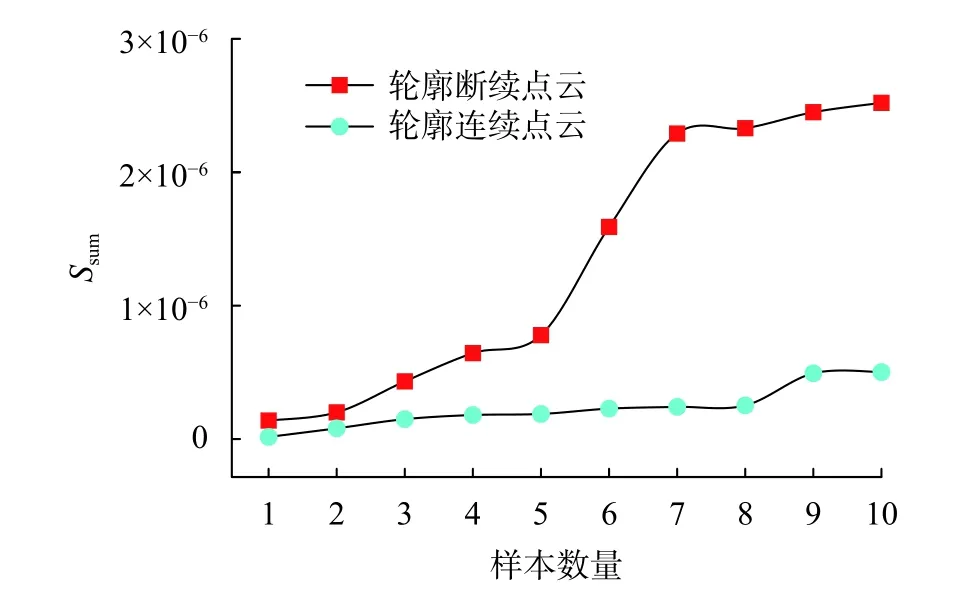
图10 两方法测量结果比较图
结合参考文献中相关数据将本方法与其他同类测量方法进行比较,如表3所示。

表3 同类方法比较
由表3可知本方法相较传统人工测量有极大优势。测量精度相对二维图像测量方法较高但尚未达到三坐标测量机的精度范围。测量速度比三坐标测量机更快但不如二维图像方法。本方法适用于无法提供垂直光源与夹具固定且震动较少的环境中。由此可见本方法在高精度、低检测速度的三坐标方法与高检测速度、精度相对较低的二维图像方法中初步取得较为理想的平衡。
4 结束语
通过对国内外相关工作的研究与发展,借助逆向工程的思路与二维图像检测的具体方法,本文提出了一种基于局部点云自动检测螺纹锥度的算法。该算法利用三维结构光相机得到轮廓断续或轮廓连续点云,在数据预处理阶段,提出基于端面轮廓的点云摆正方法将螺纹进行摆正做到在无需夹具的前提下进行检测,使用分割平面进行轮廓提取并找出合理的检测位置。在点云聚类阶段,对轮廓断续点云与轮廓连续点云分别使用不同聚类方法并提出特征点选取模型对聚类结果进行处理得到拟合锥度线所需特征点。最后对多个特征点集拟合结果进行加权融合得到锥度线斜率。
实验结果表明,提出的锥度测量算法能在一定程度上精准快速地从局部螺纹点云中完成螺纹锥度的测量。但该方法仍受限于点云预处理过程中摆正精度与特征点选取模型对数据噪点的鲁棒性。如果获取的数据噪点过多则会严重影响最终测量精度。本文下一步工作将结合数据本身结构信息改进摆正算法。同时对分割及特征点选取模型进行进一步研究优化以提高其对噪点数据的鲁棒性。
