非饱和土-结构动力响应的多耦合周期性有限元法1)

狄宏规 *, 郭慧吉 , **, 周顺华 *, 王炳龙 *, 何 超 *,

* (同济大学道路与交通工程教育部重点实验室，上海 201804)

† (同济大学,上海市轨道交通结构耐久与系统安全重点实验室,上海 201804)

** (上海申通地铁集团有限公司技术中心,上海 201103)

引言

近年来,地铁隧道车致环境振动问题日益突出,严重影响着线路周边居民的正常生活、精密仪器的正常使用及古建筑与文物的保护等[1-3].为采取有效的减(隔)振措施,迫切需要可靠的车致动力响应预测模型.

常见的地铁隧道动力响应预测模型主要包括解析(半解析)模型以及数值法模型[4].解析(半解析)模型主要有欧拉梁-地基模型[5-7]、Pip in Pip(PiP)模型[8-10]及波函数法模型[11-12]等.解析(半解析)模型计算效率较高,但难以处理不规则边界.与解析(半解析)模型相比,数值模型的优势在于可以进行更为精细化的建模,便于处理复杂的边界(界面),可考虑复杂的地基结构.常见的数值模型有二维有限元模型[13-14]、三维有限元模型[15-17].二维有限元忽略了弹性波沿隧道纵向的传播、三维有限元则占用大量的计算机资源,为兼顾二维有限元计算效率,同时考虑隧道纵向的动力传播规律,相关性学者假定模型沿纵向几何和物理性质的不变性,基于纵向Fourier或Floquet 变换,分别提出了2.5 维有限元[18-19]和周期性有限元模型[20-21].此外,为避免人工截断模型边界产生的误差,相关学者提出了边界元[22-23]、无限元[24-25]、比例边界有限元[26]、多阻尼层[27]等边界处理方法.然而上述既有的数值模型仅将土体视为单相弹性或两相饱和多孔介质,鲜见考虑地基土体的三相特性,同时无法高效考虑模型的纵向变化特性.

为此本文基于非饱和土波动方程以及渗流运动方程,结合应力、渗流边界条件,采用 Galerkin 法,推导了非饱和ub-pl-pg格式有限元方程.同时引入拉伸函数构建完美匹配层(PML)处理边界,提出了非饱和地基-结构动力响应分析的有限元-完美匹配层方法.在此基础上进一步引入自由波传播理论,将结构沿一个方向的变化处理为多耦合周期性结构,基于自由波传播常数及传播向量进行各周期性结构间的耦合,最终提出了多耦合周期性有限元法,并进行了地基-隧道-排桩系统动力响应的算例分析.

1 多耦合周期性有限元法

1.1 非饱和ub-pl-pg格式有限元推导

为实现频域内的模型求解,首先定义关于时间变量t的傅里叶变化形式

式中,ω代表时间t对应的频率;顶标“～ ”表示频域中的变量.

基于式(1)中傅里叶变化形式,根据三相介质理论[28],可得频域内三相介质波动控制方程及渗流方程分别为

式中,B11～B25表达式详见附录A.其余各变量定义可参考文献[28].

整理式(3)可得

引入应力、渗流边界条件

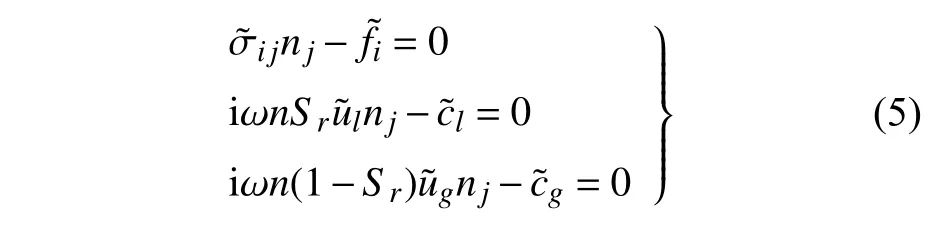
式中,f,cl,cg分别表示边界节点处外力及输入的液体、气体流速.

基于Galerkin 法,在式(2)和式(5)的基础上,引入虚位移δub以及虚孔压δpl,δpg,同时利用式(4)在计算过程中消去v,w分量,可得ub-pl-pg格式的虚原理表达式为

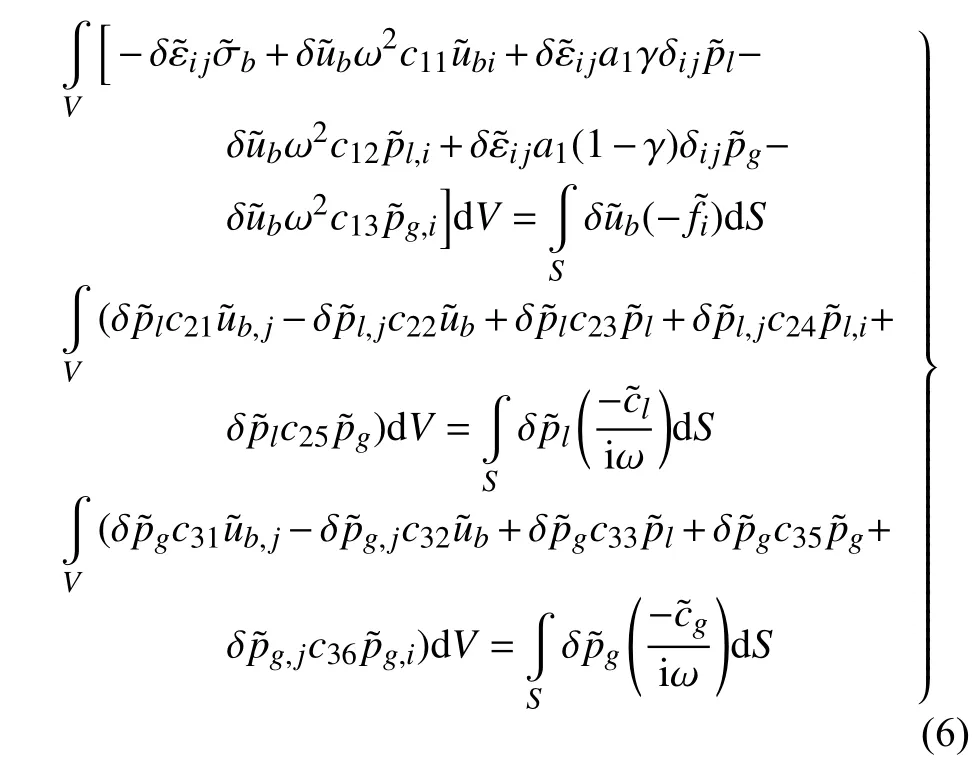
式中,各变量表达式详见附录B.

采用空间8 节点等参单元进行离散处理,可得ub-pl-pg格式的三相介质有限元表达式为

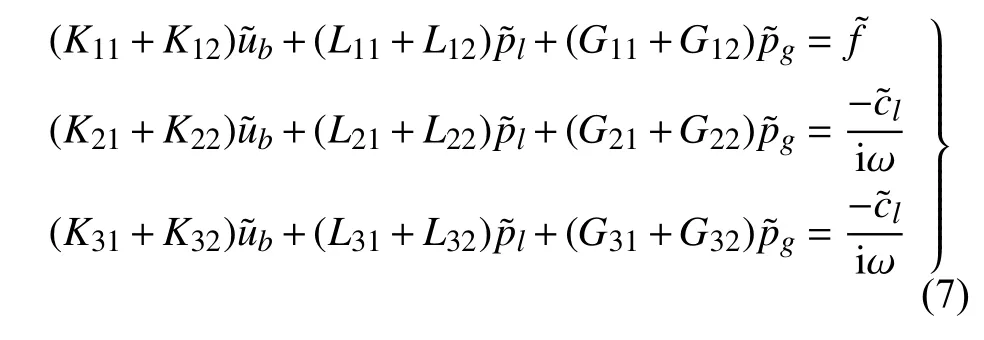
式中,各变量表达式详见附录C.

1.2 完美匹配层单元

采用完美匹配层处理模型边界,可在有限的单元内实现弹性波无反射的迅速衰减,进而截断无限域.因此引入拉伸函数[29],推导三相非饱和多孔介质完美匹配层单元

式中,顶标“↔”表示拉伸含义.

弹性波在传播过程中可分为两种波,即传播波(propagating)与隐逝波(evanescent),因此定义拉伸函数为

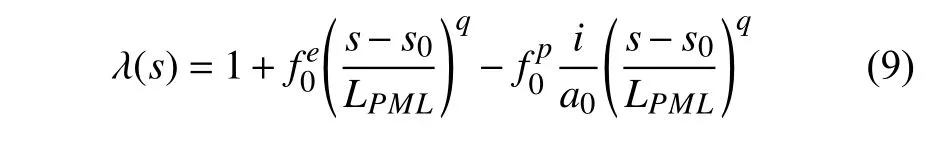
式中,a0为无量纲频率常数,a0=ωLPML/c;LPML为PML 区间长度;ω为角频率;c为弹性波波速.

为验证完美匹配层对流体中弹性波衰减的有效性,以孔隙流体影响的一维压缩波的衰减为例,假定压缩波传播中位移函数为eik(k为压缩波波数),计算从20 m 处开始坐标拉伸处理时,其位移幅值随传播距离的变化,并与无坐标拉伸时计算结果进行对比,如图1 所示.可以发现,经坐标拉伸变化后,压缩波迅速衰减,且对无拉伸处理区域内弹性波传播无影响.由此可见,合理选取坐标拉伸参数构建完美匹配层,同样可实现气相及液相中弹性波的无反射衰减.

图1 一维压缩波位移衰减对比图Fig.1 The comparison diagram of displacement attenuation of onedimensional compression wave

将式(9)代入式(7)的推导过程中,可得完美匹配层有限元表达式为

1.3 多耦合周期性有限元模型

将结构根据纵向性质的差异划分为若干个周期性结构,如图2 中的周期性结构1,2,j等.同时采用半无限周期性结构模拟纵向边界.每个周期性结构由若干相同的单元组成.为便于模型耦合求解,将载荷作用结构j划分为有载荷作用区域(jB),与无载荷作用区域(jA,jC).

图2 多耦合周期性结构Fig.2 Multi coupling periodic structure

整理式(7),可得控制方程的矩阵表达式为

式中

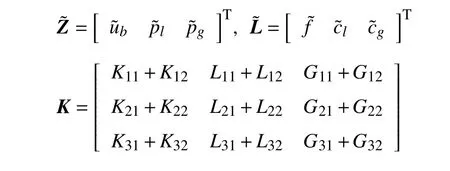
对于施加外力的周期性区域(jB),例如图2 中单元jB1,jB2,其控制方程矩阵表达式可写为

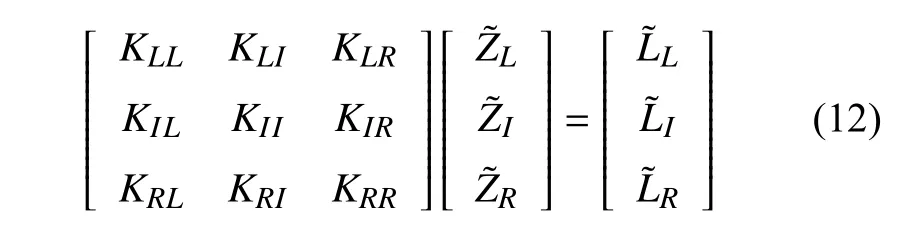
没有施加外力的周期性单元,例如图2 中单元jAi,其单元控制方程矩阵表达式可写为

根据自由波传播理论[30],当弹性波经过一个周期性单元后(图3),其前后的位移、应力、孔压等服从指数函数的传递规律,即

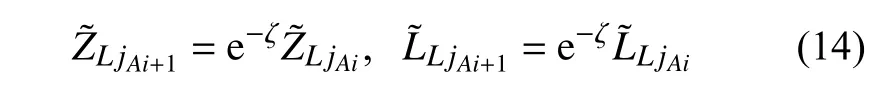
式中,ς为自由波传播常数.

由图3 可知,相邻单元间存在如下连续性条件

图3 自由波传播示意图Fig.3 Schematic diagram of free wave propagation

将式(14)和式(15)代入式(13),可得

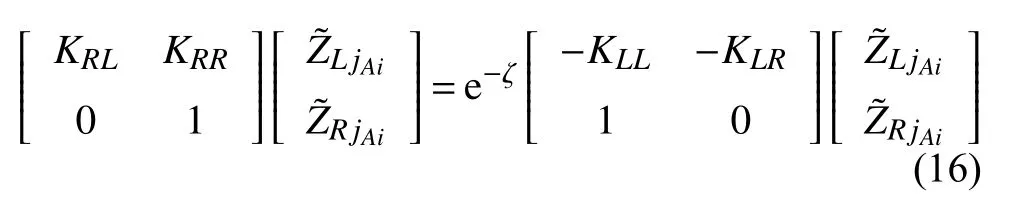
进一步整理可得

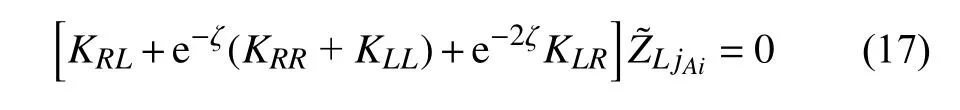
观察式(17),其为一元高次方程组,对其进行求解可得2m(m为单元左面(或右面)的自由度)个ς.由自由波传播理论可知,当ς实数部为正数时,其为由单元左面向单元右面传播的正向自由波.当ς实数部为负数时,其为由单元右面向单元左面传播的负向自由波.

求解式(17)时,每个ς对应一个特征向量即φ,将自由波传播常数ς及其特征向量φ代入式(13),可得

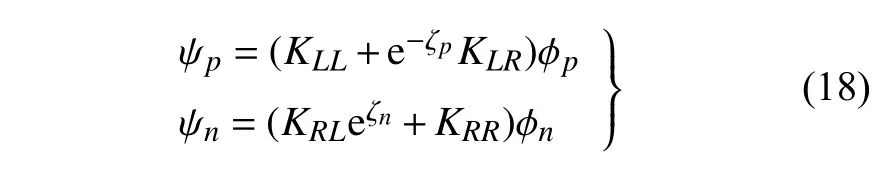
式中,φ,ψ分别为Z,L对应的特征向量;p,n分别代表正向传播波与负向传播波分量.

而单元的位移及孔压可表示为各自由波特征向量的线性组合,即

式中,α为特征向量的线性组合系数.

根据式(19)推导各部分周期性结构刚度矩阵,主要分为4 类进行讨论,即左边界、右边界、无载荷作用的周期性结构以及载荷作用的周期性结构.

(1)模型左边界

由于模型左边界左侧为半无限空间,因此不存在波的反射和折射面,其只存在负向自由波,故

由式(20)整理可得

(2)模型右边界

同理,由于模型右边界右侧为半无限空间,故

由式(22)整理可得

(3)无载荷作用的周期性结构

假定周期性结构j上无外载荷作用,如图4 所示,根据式(19)整理可得

图4 周期性结构自由波传播示意图Fig.4 Schematic diagram of free wave propagation in periodic structure

故周期性结构j左右应力、位移及孔压关系矩阵为

(4)载荷作用周期性结构

如图2 所示,载荷作用周期性结构可分为A,B,C,3 个区域,其中A,C 两区参考无载荷作用的周期性结构处理方式即可,对于载荷作用的B 区采用传统3 维有限元进行分析,即结合式(12),式(21),式(23)以及式(25)可得模型的总体刚度矩阵为

由Gaussian 消元法,可得

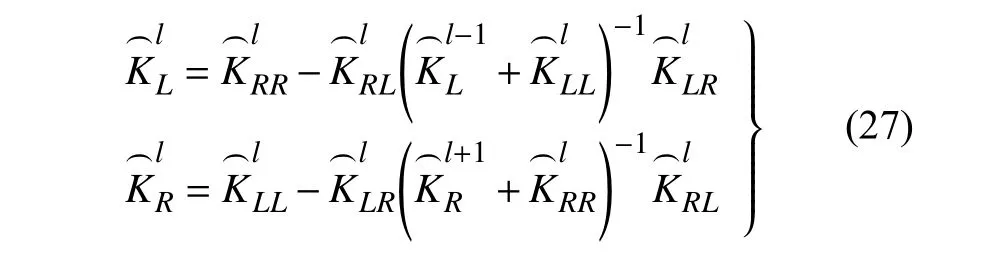
将式(27)代入式(26),化简得

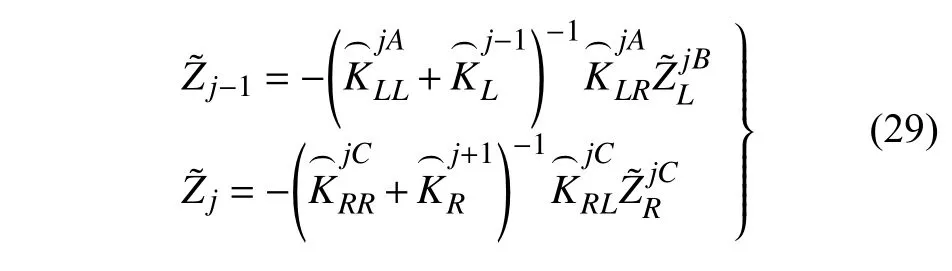
同理,可解得任意周期性结构左右界面位移、孔压值,将之代入式(24)可解的各周期性结构模态坐标值,最终由式(24)可解得频域内周期性结构内部单元的位移、孔压值.在此基础上进行Fourier 逆变化,可得时域中的解.

当载荷为移动载荷时

式中,v0为载荷移动速度,ω0为载荷激振角频率

通过离散的Fourier 变化即可实现移动载荷作用下的模型求解.

2 模型的验证

为了验证模型的可靠性,首先采用将本文模型中非饱和土参数退化的方式,来计算单相弹性地基土-隧道系统的动力响应,并与文献[31]中单相弹性地基土-隧道2.5 D FE-PML 模型的计算结果进行对比.2.5D FE-PML 模型长为14 m,宽为17 m,PML边界厚度h=1 m.多耦合周期性有限元模型横断面尺寸与2.5 D FE-PML 模型相同,纵向一个周期单元长度为0.2 m,模型简化示意如图5 所示.模型计算参数及参数退化方式参考文献[12].

图5 验证模型示意图Fig.5 Schematic diagram of validation model

图6 给出了隧道仰拱处作用单位简谐载荷(f=30 Hz,v0=0 m/s)时,不同埋深处竖向动位移ux沿水平向变化曲线.由图6 可得,两者计算结果吻合较好,一定程度上验证了本文提出的多耦合周期性有限元方法的可靠性.

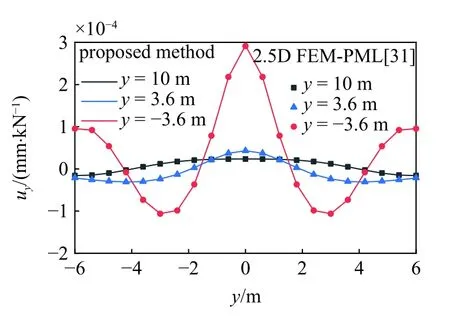
图6 多耦合周期性有限元方法与2.5 D FE-PML 模型计算结果竖向动位移ux对比图Fig.6 Comparison of vertical dynamic displacement uxof multi coupling periodic finite element model and 2.5 D FE-PML model

为了进一步验证本文方法中对于非饱和土考虑的正确性,将本文方法的计算结果与既有的解析算法[28]的计算结果进行对比,计算参数参考表1.

表1 验证模型计算参数Table 1 Calculation parameters of validation model

图7 给出了两个非饱和地基-隧道模型在隧道仰拱处(x=0 m,y=-2.75 m,z=0 m)作用单位简谐载荷(f=10 Hz,20 Hz,30 Hz,40 Hz)时,竖向动位移沿y=-3 m 的分布规律.从图7 可以看出,两者结果较为一致,进一步验证了本文提出的多耦合周期性有限元方法的可靠性.

图7 多耦合周期性有限元方法与解析算法计算结果对比图Fig.7 Comparison of calculation results of multi coupling periodic finite element model and analytical algorithm

需要指出的是,本文方法计算时主要耗时为自由波特征值的求解,以验证算例二为例,一个周期性结构单个面的自由度为5158,计算自由波传播常数耗时7065 s,后续耗时为203 s.总的来说,计算效率比解析方法略低,但与有限元-边界元方法相比,该方法在计算效率上具有较大的优势.

3 数值计算与分析

基于上述方法,以地基、隧道、隔离桩系统为例,讨论隔离桩对地表振动响应的影响,在隧道仰拱处作用固定单位简谐载荷(f=20 Hz),如图8 所示.地基、隧道模型计算参数如表1 所示,隔离桩计算参数如表2 所示.

图8 模型计算示意图Fig.8 Schematic diagram of model calculation

表2 隔离桩计算参数Table 2 The calculation parameters of isolation pile

图9 给出了无隔离桩、单排咬合隔离桩以及单排不咬合隔离桩(存在桩间距)情况下地表振动响应分布特征.可以发现,隔离桩的存在使得地表振动响应规律发生了明显变化,这主要是由于隔离桩的存在使得地基中产生了新的波反射(折射)面.靠近隔离桩附近,地表动力响应有所衰减,但距离隔离桩较远的局部位置存在振动响应放大的现象.还可以看到,与单排不咬合隔离桩相比,咬合桩的隔离效果更好.由此可见,地基中结构的纵向多耦合周期性会影响系统动力响应预测结果,因此为准确预测系统动力响应,应考虑地基结构的纵向变化特性.

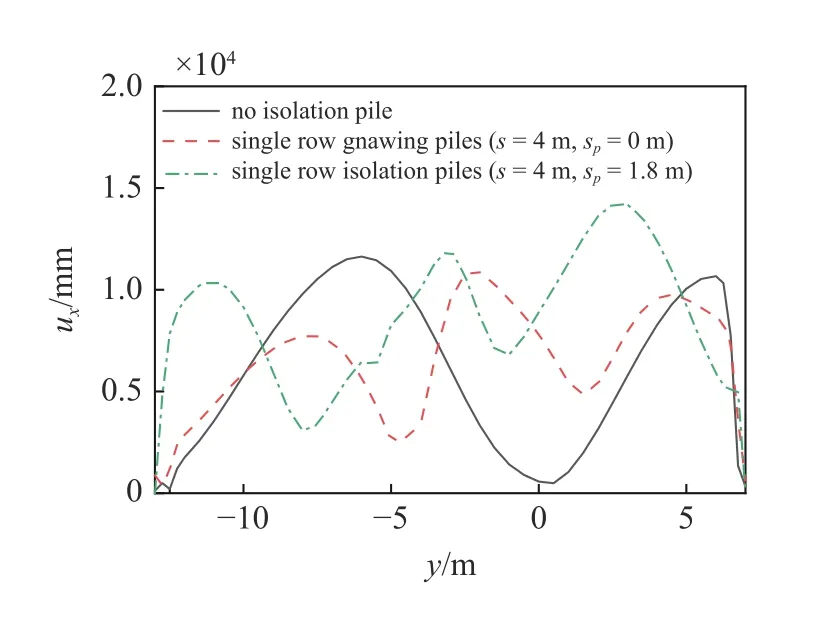
图9 不同工况下地表振动响应分布Fig.9 The distribution characteristics of surface vibration response of double row pile wall

4 结论

(1)基于非饱和土运动微分方程、连续性方程以及渗流运动方程,结合应力、渗流边界等条件,采用 Galerkin 法,推导了ub-pl-pg格式的固、液、气三相非饱和介质有限元表达式.相比于ub-v-w格式有限元单节点的9 个自由度,ub-pl-pg格式的有限元单节点减少至5 个自由度,大大节省了计算资源.

(2)基于自由波传播理论,求解自由波传播常数及自由波特征向量,基于自由波传播常数及自由波特征向量求解各周期性结构刚度矩阵,在此基础上结合传统有限元、完美匹配层单元,提出了多耦合周期性有限元法,将该方法分别与2.5 维有限元法及解析算法计算结果相对比,验证了该算法的可靠性.

(3)多耦合周期性有限元法具有可考虑结构沿纵向变化特性的优点.其与解析方法相比,计算效率略低,但与有限元-边界元方法相比,该方法在计算效率上具有一定优势.地基中结构的纵向变化特性会影响系统的动力响应,因此,进行动力响应预测时,应考虑地基中结构沿纵向的变化特性.

附录

附录A

附录B

附录C