基于径向基点插值法的旋转Mindlin 板高次刚柔耦合动力学模型1)

杜超凡 * 郑燕龙 * 章定国 周晓婷 *

* (扬州大学建筑科学与工程学院,江苏扬州 225000)

† (南京理工大学理学院,南京 210094)

引言

在现代工程领域中,随着航空航天和民用机械工程等领域的快速发展,对柔性多体系统在高速化及大变形工况下的可靠性要求越来越高.许多构件如太阳能帆板、风力发电机叶片、直升机旋翼及涡轮机叶片等都属于柔性构件搭载于刚性主体的刚-柔耦合结构.这类结构在经历大范围刚体运动的同时还存在着柔性构件的变形,且相互耦合,呈现出的动力学行为十分复杂.由于对这类经历大范围运动柔性梁的刚-柔耦合动力学行为的研究比较成熟,因此常将这类板式结构简化为一维梁进行建模分析[1-3].这种简化往往只适用于长宽比很大的细长构件,对于长宽比相差不大的板式结构,如太阳能帆板等这种简化显然是不合理的,仿真结果会有很大误差,必须用板的理论来建模分析[4-11].从国内外学者研究中发现,对做大范围运动矩形板的研究有两个共同点:一是变形场的离散方法都是假设模态法或有限元法[12-13];二是在建模过程中,大都采用忽略剪切变形的薄板理论,同时引入小变形假设,认为与非线性耦合项相关的一些高阶项可以直接去掉,并不影响最终结果.这就导致两点不足:一是变形场离散方法的单一,在旋转柔性梁的分析中已经说明了假设模态法的不足[14-15],而有限元法又存在网格畸变和难以构造高阶形函数的问题;二是随着柔性构件尺寸、厚度的增大或构件材料柔性的增加,被省略的剪切变形和非线性耦合项相关的高阶项的影响将逐渐增大[16-19],必须考虑其影响建立更加精确的高次耦合动力学模型.陈思佳等[20]考虑了非线性耦合项的高阶项,建立了既适用于小变形又适用于大变形问题的旋转柔性梁的高次刚柔耦合动力学模型,弥补了一次近似耦合模型在处理柔性梁大变形问题上的不足.因此,为了得到更精确的仿真结果,使用新的变形场离散方法和依据中厚板理论建模[21-23]获得更精确的动力学方程将显得很有必要.无网格法作为一种新的变形场离散方法,已广泛应用于板的静力学和自由振动分析中[24-30],但在柔性多体系统领域鲜有报道[31-32].将其应用到做大范围转动的矩形板中,将极大丰富柔性多体系统领域中的变形场离散方法.

本文采用无网格径向基点插值法(RPIM)描述柔性板的变形场,考虑经典薄板理论中被忽略的剪切变形的影响,保留动能中与非线性耦合变形量相关的高阶项,同时考虑了板的平动,建立了较为完整的旋转矩形板高次刚-柔耦合动力学模型.该模型既能处理薄板问题,又能处理中厚板问题,既能处理小变形问题,又能处理大变形问题.将仿真结果与传统的假设模态法和有限元法对比,表明径向基点插值法的正确性,同时说明无网格法用于该领域的可推广性.

1 旋转Mindlin 板动力学建模

1.1 系统的动能和势能

图1 所示为做大范围运动的矩形板模型,其中坐标系O-XYZ为惯性坐标系,o-xyz为连体坐标系,且连体坐标系所在平面与薄板未变形的中面重合,其3 个方向的单位矢量分别为e1,e2,e3.板长为L,宽为H,厚度为h,密度为ρ,弹性模型为E,泊松比为μ.

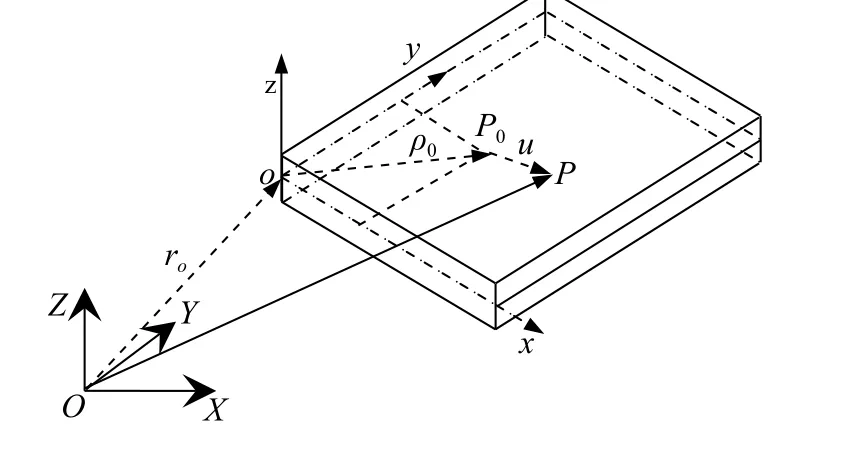
图1 作大范围运动的矩形板Fig.1 Rectangular plate with large overall motion

P0为变形前板中面上一点,变形后移至P点,变形位移矢量为u,在连体坐标系下各分量为(u1,u2,u3).基于Mindlin 板理论,板中任意一点变形位移矢量为u,在连体坐标系下为各分量为(u1,u2,u3).其中纵向位移u1,u2可用板中面上(z=0)的变形u01,u02表示为

式中,w1和w2分别为板中面内沿x和y方向的实际伸长量,为二次耦合变形量,传统的零次近似模型建立在结构动力学小变形假设的基础上,并没有考虑二次耦合变形量.φx和 φy分别为横截面相对于y轴和x轴的转角.任意P点在惯性坐标系O-XYZ下的速度矢量可表示为

式中,Vo和 ωA分别为连体坐标系相对于惯性坐标系的速度和角速度矢量,ρ0为点P0在连体坐标系中位置矢量,VPA为P点相对连体坐标系的速度矢量.各矢量在连体坐标系的分量形式为

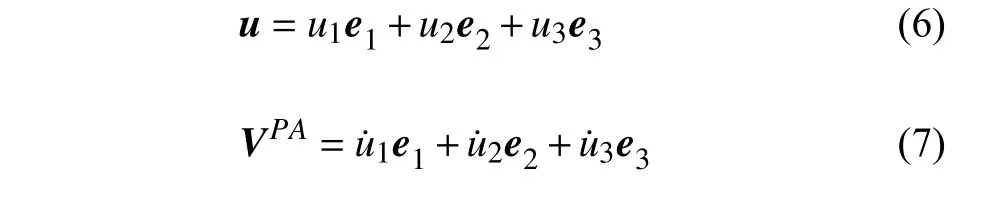
将以上各式代入式(2)中,可得

系统的动能为

考虑剪切变形的影响,任一点处的应变为

对各项同性材料,其应力为

系统势能为

式中,U1和U2分别为板面内变形能、板横向弯曲和剪切变形能,表达式分别为

1.2 系统的动力学方程

将问题域离散为若干个节点,将矩形板问题域用N个场节点表示,如图2 所示.形函数由支持域中所包含的节点形成,具体表达式在文献[31]中有详细阐述.

图2 矩形板无网格法离散Fig.2 Meshless discretization of rectangular plates

与薄板理论建模不同,Mindlin 板理论由于考虑横向剪切应力对变形的影响,因此变形前垂直于中面的直法线变形后将变为曲线,横截面相对于x轴和y轴的转角不再是薄板理论中挠度u3的一阶导数,为独立变量,表示为

式中,n为计算点支持域内的节点数,φ1i(x,y),φ2i(x,y),φ3i(x,y) ,φ4i(x,y) ,φ5i(x,y) 为支持域内对应节点的形函数,通常令 φji(x,y) (j=1,2,···,5) 相同.q1(t)和q2(t) 为相应节点面内纵向变形位移列阵,q3i(t)为相应节点横向变形及截面转角组成的列阵.对 应u3和两个转角的形函数行阵及q3i(t) 的表达式为

为表述方便,以下表达式中略去自变量x,y,t.

令 Φ4=zφ4,Φ5=zφ5,将式(15)代入式(1),得变量u1,u2及其速度为

式中,H1(x,y)和H2(x,y) 为耦合形函数,表示如下

下标中“,”表示对坐标求偏导数.

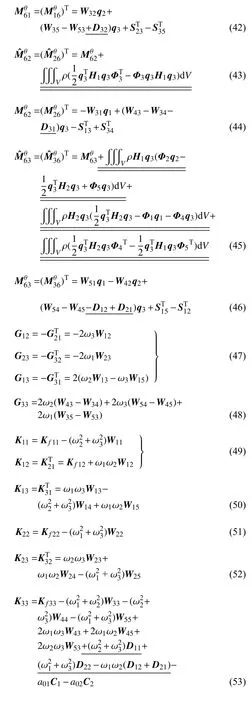
式中,a01,a02,a03为基点加速度在连体坐标系下的分量,表达式为

各常数阵为

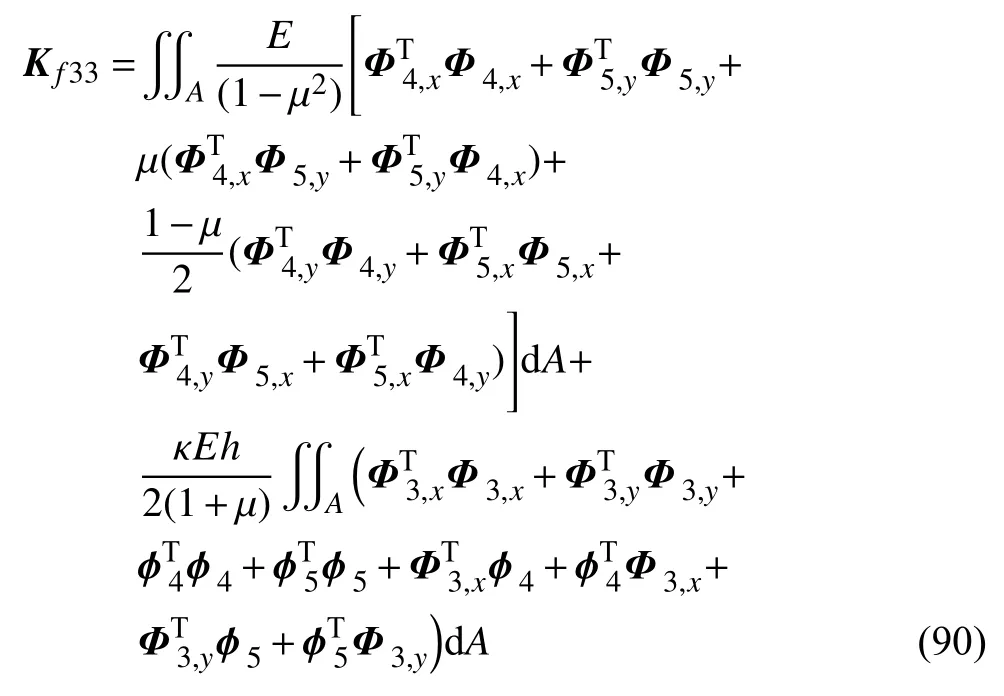
式(24)即为系统的高次刚-柔耦合动力学方程,该模型既能处理大变形问题又能处理小变形问题,弥补了一次近似模型在处理大变形问题时的不足.其中带双下划线的项是由于考虑了非线性二次耦合变形量的高阶项而推导出的.若去掉这些双下划线的项,则式(24)退化为一次近似模型;若去掉单下划线的项,则退化为零次近似模型.

2 数值仿真

2.1 剪切闭锁

当使用Mindlin 厚板理论分析薄板问题时,往往会发生剪切闭锁现象.为了使推导的动力学方程能正确仿真薄板问题,应首先对剪切闭锁现象进行研究.

考虑如图3 所示的矩形板,其参数为:长a=10.0 m,宽b=10.0 m,弹性模量E=1.0 GPa,泊松比μ=0.3,厚度为h.定义一个挠度系数 ξ,表达式为

图3 矩形板受力图Fig.3 Force diagram of rectangular plate

式中,wmax为板的最大挠度值,P为集中力载荷,D为板的弹性刚度,表达式为

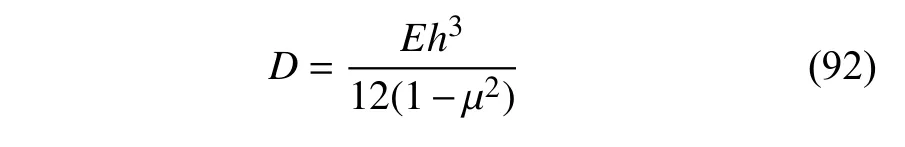
表1 为不同节点个数下,使用径向基点插值法求得的四边简支、厚长比h/a=0.01 且中心点受集中力P=100 N 作用的薄板挠度系数.CPT 和FSDT 分别表示经典薄板理论和Mindlin 板理论.从表中可知,当节点个数为17 × 17 左右,可得到与文献基本相同的解,基于Mindlin 板理论的解比经典薄板理论解更精确.在以下仿真中,离散节点个数都选取17 ×17.

表1 四边简支、中心点受集中力作用的薄板挠度系数 (h/a=0.01)Table 1 Deflection coefficient of thin plates subjected to concentrated force at the center point with SSSS boundary condition (h/a =0.01)

表2 为不同边界条件的厚长比h/a=0.1,中心点受集中力P=100 N 作用的厚板挠度系数,分别使用经典薄板理论(CPT)和Mindlin 板理论(FSDT).为表述方便,做如下规定,板四边按左上右下顺序排列,简支边界用S 表示,固支边界用C 表示,如SCSC 表示左右边界简支,上下边界固支,SCCS 表示左下简支,右上固支.从表中可知,基于Mindlin 板理论的结果与文献[33]提供的解析解结果基本一致,且总比基于经典薄板理论的结果大.同时说明经典薄板理论只能处理薄板问题,而Mindlin 板理论即可以处理厚板问题,又可以处理薄板问题,并且精度更高,因此具有更广泛的应用价值.

表2 不同边界条件和受力情况下厚板挠度系数(h/a=0.01)Table 2 Deflection coefficient with different boundary conditions and forces (h/a=0.1)

当板厚度更薄即厚长比更小时,基于Mindlin 板理论将出现剪切闭锁现象.在有限元法中,通常通过构造高阶单元形函数来消除剪切闭锁现象.根据这一思想,在无网格法中同样可以通过构造高阶形函数来消除剪切闭锁现象,而可方便的构造高阶形函数正是无网格法的优势,通过添加高阶多项式基函数即可完成.表3 表示受集中力作用,四边简支的矩形板在不同厚长比下的挠度系数 ξ .从表中可明显看出,当厚长比小于0.001 时,添加低阶多项式的径向基点插值法出现剪切闭锁现象,求得的挠度系数比解析解小很多.当添加的多项式为15 和18 项时,可消除剪切闭锁现象.厚长比为0.000 1 的板是极端情况,现实中并不存在,因此对于基于Mindlin 板理论的径向基点插值法,添加15 项多项式基函数即可消除剪切闭锁现象.需要注意的是,此时需增大支持域尺寸,否则将导致力矩矩阵不可求逆,支持域的无量纲尺寸通常取为 αs=4.1 .当厚长比较大即不发生剪切闭锁现象时,添加多项式基函数对解的精度影响并不大,因此对于中厚板,为提高计算效率,可选择不添加多项式基函数.图4 所示为受集中力作用四边简支板在不同厚长比下,数值解与文献提供的解析解的比值.从图中可更直观地看出,当厚长比小于0.001 时,添加低阶多项式基函数发生明显的剪切闭锁现象,当多项式基函数为15 和18 项时,可消除剪切闭锁现象.当厚长比较大时,多项式基函数对结果影响并不明显.

图4 多项式基函数对剪切闭锁的影响Fig.4 Influence of polynomial basis function on shear locking

表3 受集中力作用四边简支板不同厚长比下的挠度系数Table 3 Deflection coefficient with different aspect ratios

2.2 大范围运动已知的动力学仿真

考虑如图5 所示的作定轴转动的中心刚体-矩形悬臂板,与中心刚体固连.中心刚体以角速度 ω 绕y轴旋转,板的材料参数为:长度a=1.828 8 m,宽度b=1.219 2 m,厚度h=2.54 mm,弹性模量E=70 GPa,密度ρ=2000 kg/m3,泊松比取0.3,中心刚体半径R取0.ω1=ω3=0, ω2=ω , ω˙1=ω˙3=0 ,ω˙2=,给定的角速度规律为

图5 作定轴转动矩形薄板Fig.5 Configuration of rotating cantilever plate

式中,T=30 s .

图6 为Ω=20 rad/s 时,本文方法与参考文献[6]中矩形薄板外侧角点M的横向变形位移历程的对比.从图中可以看出,本文RPIM 的仿真结果与参考文献的仿真结果高度吻合,验证了本文动力学模型的正确性.图7 所示分别为 Ω=0.2 Hz和Ω=0.75 Hz时板外侧角点M的横向变形.从两图中可以看出,当转速较低时,零次近似模型、一次近似模型和高次模型的差别并不大,但零次近似模型的最大值比一次近似模型和高次模型的稍大.当转速较高时,零次近似模型与另两种模型出现很大区别.零次近似模型结果发散,仿真失败,而一次近似模型和高次模型结果收敛,且仿真结果高度吻合.这与旋转柔性梁中的分析结论相同,说明零次近似模型忽略耦合变形量存在建模理论的缺陷,其刚度阵随着转速的增大而减小,产生动力柔化效应,这也是造成在转速较低时其变形比一次近似模型大的原因.而一次近似模型和高次模型考虑了耦合变形量,其刚度阵随着转速的增大而增大,产生动力刚化效应,符合实际情况,同时也说明本文所建高次模型的正确性.进一步研究发现,对于大范围运动已知的情况,随着转速的增加,高次模型并没有比一次近似模型优越,相反使计算效率降低很多.因此对于该类问题的研究优先选用一次近似模型.

图6 外侧角点横向变形比较Fig.6 Comparison of lateral deformation of outer corner point M

图7 矩形薄板外侧角点的横向变形Fig.7 Lateral deformation of outer corner point M

图8 为 Ω=0.2 Hz 时使用不同离散方法获得的一次近似模型板外侧角点M的横向变形,其中假设模态法和有限元法基于经典薄板理论,径向基点插值法基于Mindlin 板理论.有限元法分别使用8 ×4 个矩形单元和2 × 8 × 4 个三角形单元,径向基点插值法离散为16 × 8 个节点.从图中可看出,各离散方法的仿真结果基本一致.图8(b)为匀速转动阶段的局部放大图,同样可看出各离散方法的响应频率及振幅基本一致.图9 为 Ω=0.2 Hz 时使用不同离散方法获得的一次近似模型板外侧角点M的横向变形速度.如图所示,各离散方法的仿真结果基本一致,从局部放大图中可知,大范围运动转速恒定时的速度响应频率和振幅也基本一致.

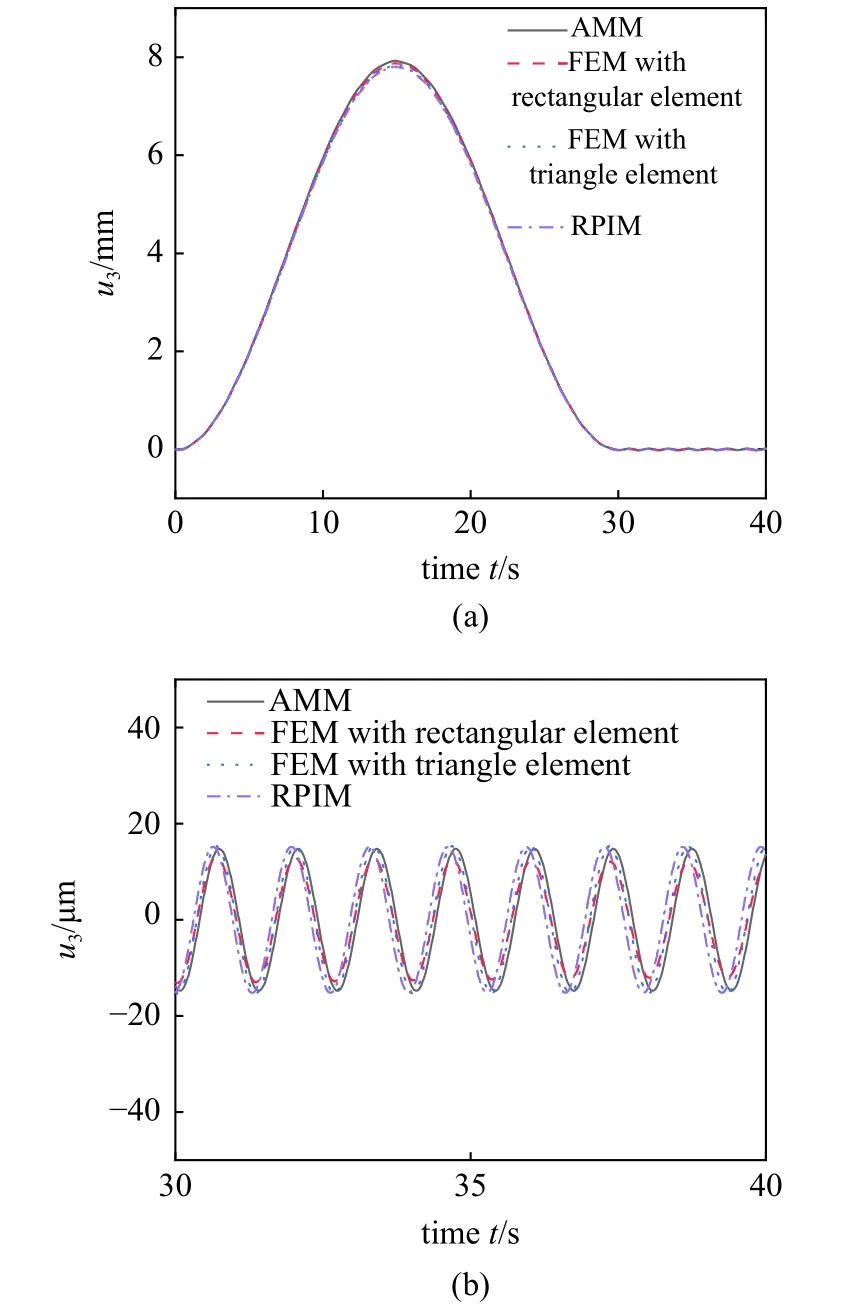
图8 矩形薄板外侧角点横向变形(Ω=0.2 Hz)Fig.8 Lateral deformation of outer corner point M(Ω=0.2 Hz)

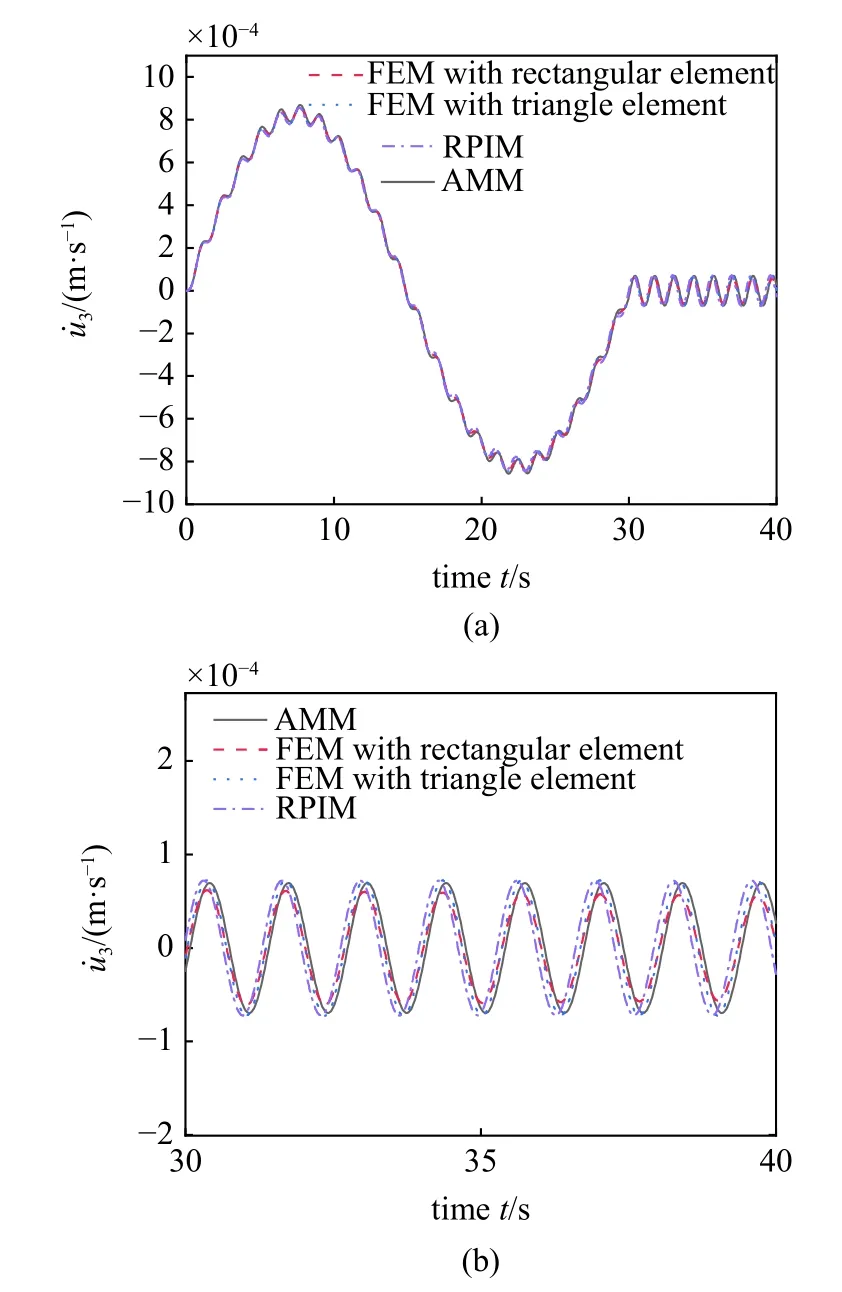
图9 矩形薄板外侧角点横向变形速度(Ω=0.2 Hz)Fig.9 Lateral deformation rate of outer corner point M(Ω=0.2 Hz)

图10 为 Ω=0.75 Hz 时使用不同离散方法获得的一次近似模型板外侧角点M的横向变形.从图中可看出,各方法的仿真结果基本一致.图10(b)为匀速转动阶段的局部放大图,各方法的响应振幅和频率并没有 Ω=0.2 Hz 时吻合的好,但也相差不大.其中假设模态法、三角形单元有限元法的仿真结果最吻合,径向基点插值法的响应振幅最大,而矩形单元有限元法响应振幅最小.从纵坐标的数量级来看,这种差别是极微小的,都能满足实际的工程需要.图11为 Ω=0.75 Hz 时使用不同离散方法获得的一次近似模型板外侧角点M的横向变形速度.同样的,各方法的仿真结果基本一致.图11(b)为匀速转动阶段的局部放大图,如图所示,与横向变形的局部放大图中的变化相同,我们可得出同样的结论.

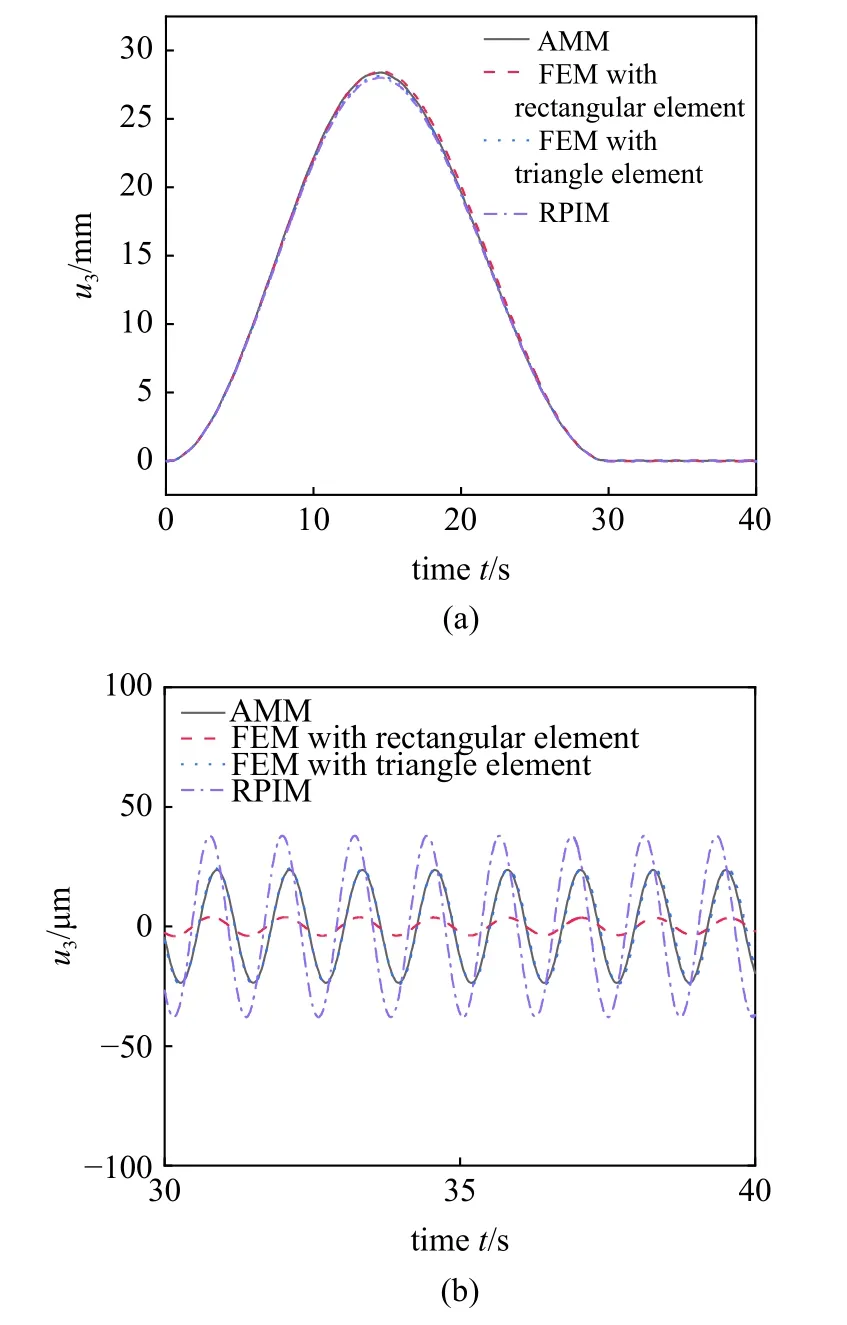
图10 矩形薄板外侧角点横向变形(Ω=0.75 Hz)Fig.10 Lateral deformation of outer corner point M(Ω=0.75 Hz)

图11 矩形薄板外侧角点横向变形速度(Ω=0.75 Hz)Fig.11 Lateral deformation rate of outer corner point M(Ω=0.75 Hz)

图12 为 Ω=10 Hz 时使用不同离散方法获得的一次近似模型板外侧角点M的横向变形.从图中可看出,仿真结果在10 s 之前基本一致.随着仿真时间的增加,有限元法结果发散,计算失败.而径向基点插值法结果收敛,体现了无网格法计算上的优势.

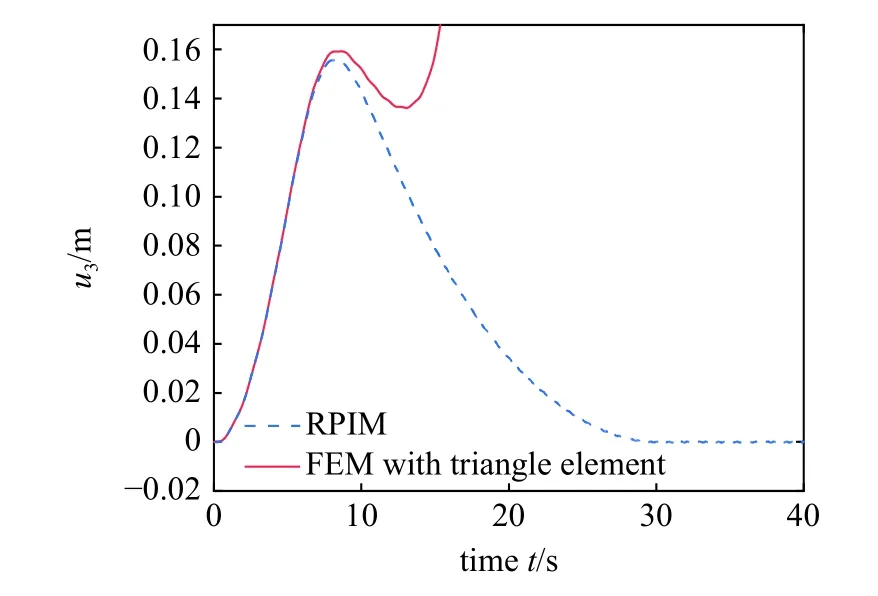
图12 矩形薄板外侧角点横向变形(Ω=10 Hz)Fig.12 Lateral deformation of outer corner point M(Ω=10 Hz)

图13 为在三维空间转动的矩形板,矩形板固结于一绕Y轴作定轴转动的中心刚体上.惯性坐标系O-XYZ的原点O和矩形板连体坐标系o的距离r=0.2 m.连体坐标系中单位方向矢量e1和e2分别和未变形矩形板长度和宽度平行,e3垂直于矩形板中面.(e1,e2,e3)可由惯性坐标系O-XYZ经过三次绕轴旋转获得,3 个欧拉角和系统所有参数与文献[6]相同.图14 为Ω=10 rad/s 时,矩形板外侧角点P横向变形同文献[6]对比图,从图中可以看出,本文的仿真结果与参考文献的仿真结果高度吻合,验证了本文动力学模型处理三维算例的正确性.

图13 三维空间转动板Fig.13 Rotating plate in 3-D

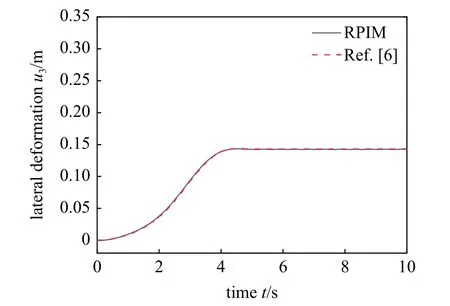
图14 矩形薄板外侧角点P横向变形(Ω=10 rad/s)Fig.14 Lateral deformation of outer corner point P(Ω=10 rad/s)

2.3 大范围运动未知的动力学仿真

板的材料参数为:长度a=1.0 m,宽度b=0.5 m,厚度h=2.5 mm,弹性模量E=70 GPa,密度ρ=3000 kg/m3,泊松比取0.3,中心刚体半径R取0.假定施加在中心刚体绕y轴方向的外力偶矩为

其中,T=2 s.

图15 所示分别为τ0=5 N·m 和τ0=70 N·m 时一次近似模型和高次模型板外侧角点M的横向变形.从两图中可以看出,当τ0=5 N·m 时,一次近似模型和高次模型的仿真结果高度吻合,此时柔性板外侧角点最大变形位移约为0.03 m,属于小变形,说明两种模型均适于小变形情形.当驱动力偶矩τ0=70 N·m,一次近似模型结果发散,仿真失败,而高次模型仿真结果仍然收敛.此时柔性板外侧角点最大变形位移约为0.4 m,对于长为1 m 的板而言属于大变形.由此可知,对于大变形情形,一次近似模型并不适用,而高次模型仍然适用.同时也说明二次耦合变形量的高阶项在大变形情形下尤为重要,不能忽略.

图15 矩形薄板外侧角点横向变形Fig.15 Lateral deformation of outer corner point M

3 结论

本文采用无网格径向基点插值法描述柔性板的变形场,基于一阶剪切变形理论,保留动能中有关非线性耦合项的高阶量,通过构造高阶形函数避免了径向基点插值法出现剪切闭锁的现象,建立了能处理不同厚长比的作大范围运动矩形板的高次刚-柔耦合动力学模型.通过静力学算例验证避免剪切闭锁方法的正确性.分别运用假设模态法、有限元法和径向基点插值法及两种板的建模理论对作定轴转动的中心刚体与悬臂板的动力刚化问题进行动力学仿真,其仿真结果与已有文献一致,说明本文径向基点插值法建立的模型是正确的,也说明了在同等条件下,无网格法具有计算上的优势.比较了传统的零次近似模型、一次近似模型和高次模型之间的差异,发现传统的零次近似模型只能适用于转速很低的情况,适用范围狭窄,而一次近似模型和高次模型既适用于低转速又适用于高转速的情况,证明了考虑耦合变形量的必要性.研究发现,高次模型由于考虑了非线性耦合变形项的高阶量,相对于一次近似模型,计算效率降低很多,因此仿真时优先选用一次近似模型;一次近似模型只适用于小变形情况,而高次模型既适用于小变形情况,又适用于大变形情况.