基于CNN-BiGRU的空间目标RCS异常检测方法

亓铭瑞,蒋李兵,王 壮

(国防科技大学 自动目标识别重点实验室，长沙 410073)

0 引言

利用空间目标雷达散射截面(radar cross section，RCS)对目标状态信息进行推断反演,对空间监视具有重要意义[1]，其中基于RCS的姿态异常检测能够为航天器在轨状态分析与后续抢修或应急补发提供依据。航天器正常工作时受控制系统作用一般保持三轴稳定姿态，当发生异常时，其在摄动里的作用下表现为绕主惯量轴的翻滚运动[2]。RCS具有姿态敏感性，利用目标RCS的时变特征，可以实现对空间目标的异常检测。传统基于RCS序列的空间目标异常检测方法主要可以归为两类：一类为利用目标RCS序列的时域变化特征(周期性，随机性)进行姿态稳定性判断，如周期图法[3]，通过对RCS序列对应频谱响应曲线进行峰值检测，判断RCS序列周期性，进而判断目标是否失控翻滚。游程检验法[4-5]将目标RCS序列转换为游程序列，通过随机性检验判断目标姿态稳定性。另一类首先将RCS序列进行域变换，基于变换域特征对不同姿态下的RCS序列进行分类与识别，进而判断目标姿态稳定性，如小波分解法[6]。这类方法对于单脉冲体制雷达，短时间就能获得目标较长RCS观测序列的情况下，具有较好的检测效果。然而，相控阵雷达在实际任务中往往要对多个目标进行跟踪监视，作用于单个目标的观测资源会受到限制，导致获取单个目标RCS数据率一般比较低，相同观测时间内获得RCS序列较短。传统方法在提取RCS序列特征时主要对其整段数据的全局特征进行提取，未考虑不同时间尺度的局部特征及这些特征间的时序依赖关系，因此当数据量不足以有效反映序列全局属性时，检测准确率就会降低。

神经网络通过各个网络层对数据本质特征进行非线性抽象，能够实现对数据深层特征的提取，简化了复杂的特征工程，针对少量数据也能实现有效的特征提取。此外，空间监视任务中会积累大量目标RCS观测数据，这些长期积累的历史数据隐含了目标丰富的特征信息。传统方法在提取RCS序列特征时，人的主观经验起主导作用，而忽略了历史数据所包含的对目标RCS特征的客观描述，造成了对这些宝贵历史数据的浪费。鉴于神经网络具备从数据中抽象高层次共性特征描述的能力，可以利用其在数据表征上的优势，将深度学习与姿态异常检测进行有机结合，有助于建立鲁棒性更强的判别模型。基于此，本文提出了基于卷积神经网络(convolutional neural networks，CNN)与门控单元循环网络(bidirectional gated recurrent unit，BiGRU)的空间目标RCS异常检测方法，通过级联CNN和BiGRU，获取RCS序列高层次特征在时序上的相关关系，实现对异常RCS的分类与识别。

1 空间目标不同姿态RCS散射特性

不同目标，不同构件的RCS散射特性一般不同。大部分在轨航天器尺寸较大，一般处于高频区，故目标整体散射场可以视为各个构件独立散射场的叠加。设雷达的发射信号为:

Et=E0exp(jωt)

(1)

若目标上某构件散射中心P(xi,yi)与目标中心的距离为RΔi，雷达视线方向目标与雷达距离为R0(t)，雷达LOS方向与目标主轴夹角为θ，则雷达与该散射中心的距离为：

R(t)=R0(t)+RΔi=R0(t)+yicosθ-xisinθ

(2)

目标反射回波可以表示为：

(3)

其中δ(xi,yi)为散射系数，λ为雷达发射信号波长，2L为目标尺寸，ω为目标转速，相位补偿后回波可以表示为：

(4)

由式可以看出，空间目标RCS会随姿态角的改变而发生变化。正常工作的卫星在轨运行姿态一般为三轴稳定姿态，卫星的姿态角变化较小，对应RCS变化幅度小，但卫星目标上构件的微动会引起整体RCS值的变化，如太阳能帆板的转动、天线的旋转等，因此三轴稳定姿态下的空间目标其RCS测量值为一个确定常量与一个随机量的叠加。当卫星发生异常时，进行翻滚运动，其 RCS序列呈周期性变化，虽然和三轴稳定姿态一样会有随机量的叠加，但序列的周期分量趋势一般不会被掩盖[7]。

2 神经网络RCS特征提取

2.1 基于一维CNN的RCS特征提取

本文采用一维CNN对RCS序列不同时间尺度的特征进行提取，如图1所示，每进行一次卷积，特征向量相应增加一个特征值，完成一次卷积后，卷积核按照指定步长沿序列滑动，继续执行卷积操作，进而实现对RCS序列不同时间尺度的局部特征进行提取。一维卷积的数学表示为：

图1 一维卷积原理图Fig.1 Schematic diagram of one-dimensional convolution

(5)

其中w(k)为第k个卷积核参数，x(m+k)为输入RCS序列第(m+k)元素的值，y(m)为输出特征向量第m元素的数值，b为偏置项，f为激活函数。对于多层一维卷积网络，若卷积层输入为上一层提取的特征向量，则本层卷积可以实现特征向量间的非线性映射。

2.2 基于BiGRU的时序特征提取

长短期记忆网络(long short term memory, LSTM)作为循环神经网络(recurrent neural network, RNN)的变体，解决了RNN随着递归量的增加出现的梯度消失或梯度爆炸问题[7]。门控循环单元(gated recurrent unit, GRU)为LSTM的简化网络模型，其内部核心结构为更新门与重置门。GRU在保持LSTM性能的同时简化了网络结构，减少了网络参数，显著提高网络的收敛速度。单向GRU网络中，节点状态均为从前至后单向传递，对于时间序列当前状态只能利用过去历史信息获得，使得网络难以学习序列前后完整特征，因此本文拟采用BiGRU提取特征向量的时域特征。BiGRU网络由沿时序正反两个方向的循环网络构成，其结构如图2所示，设输入特征向量为X=[x1,x2,…,xt-1,xt,…,xT]，则更新门ut、重置门rt在t时刻的状态可以表示为：

图2 BiGRU结构图Fig.2 Network structural diagram of BiGRU

ut=σ(Wu[ht-1,xt])

(6)

rt=σ(Wr[ht-1,xt])

(7)

(8)

(9)

(10)

这种结构使得网络既能够获得正向长短期的信息，也能获得反向未来的依赖信息。

3 RCS异常检测方法

3.1 异常检测流程

基于空间目标RCS的姿态异常检测处理流程如图3所示，整个处理流程分为：(1)网络训练；(2)数据划分；(3)异常检测3个部分。首先仿真目标RCS数据，通过时间窗对整个观测弧段数据进行采样，得到分段RCS序列，进而构建训练数据集，之后进行多轮训练对网络进行迭代优化，得到网络模型参数。对于RCS测量数据，同样采用滑动时间窗进行积累，时间窗长度为M，滑动步长为N，即初始积累RCS数据长度为M，之后每新增N个数据，进行一次姿态判别，相邻时间窗姿态判别结果发生改变时，则判断状态发生异常。

图3 异常检测流程图Fig.3 Flow diagram of anomaly detection

3.2 CNN-BiGRU网络结构设计

本文采用网络结构如图4所示，CNN网络采用3层结构(超过3层检测准确率没有明显提升，网络收敛速度反而变慢)，每层由卷积层，批归一化(batch normalization，BN)层以及线性修正单元(rectified linear unit，ReLU)激活函数组成，用于提取RCS序列各时段的局部特征向量。卷积核数量为{128，256，128}，适当增加网络卷积核数量有助于提升网络最大性能，网络性能达到最大后，卷积核数量越多，网络需要学习的超参数大幅增加，网络将变的难以收敛，导致网络最大性能下降。不同目标RCS分布的差异性会随着网络的迭代不断累积放大，造成网络难以收敛，故加入BN层对数据进行规范化以加快网络的收敛速度，提高网络的泛化能力[8]。ReLU函数是一种非线性激活函数，能够增强网络对复杂非线性特征的拟合能力；BiGRU用于提取特征向量沿时序正、反两个方向的关联特征，GRU单元的数量从文献[1，2,4,6]中搜索，找到最佳的数量，隐藏层特征维度为128，隐藏层后设置0.2比重的随机丢失机制以防止训练过拟合；最后通过全连接层与Sigmod函数进行特征整合，输出分类结果。

图4 CNN-BiGRU级联网络结构图Fig.4 Cascaded network structural diagram of CNN-BiGRU

3.3 数据集构建

利用FEKO电磁模拟软件，仿真3种卫星目标RCS数据。在轨目标位于远场，故雷达信号波形采用平面波，信号载频分别采用500 MHz、2 GHz、3 GHz 3种频段，模拟方法为物理光学法。仿真目标三轴稳定姿态RCS数据时，固定雷达视角，使目标的三维姿态进行小范围变化；仿真目标翻滚姿态时，使目标绕主轴按照一定的角速度进行旋转，并加入姿态扰动。如图5所示为3个卫星目标的三维模型以及不同姿态下部分时间窗RCS仿真序列。获得目标雷达RCS序列数据后，将数据按照如图6所示的滑动窗口进行划分，窗长M=100，步长N=20。

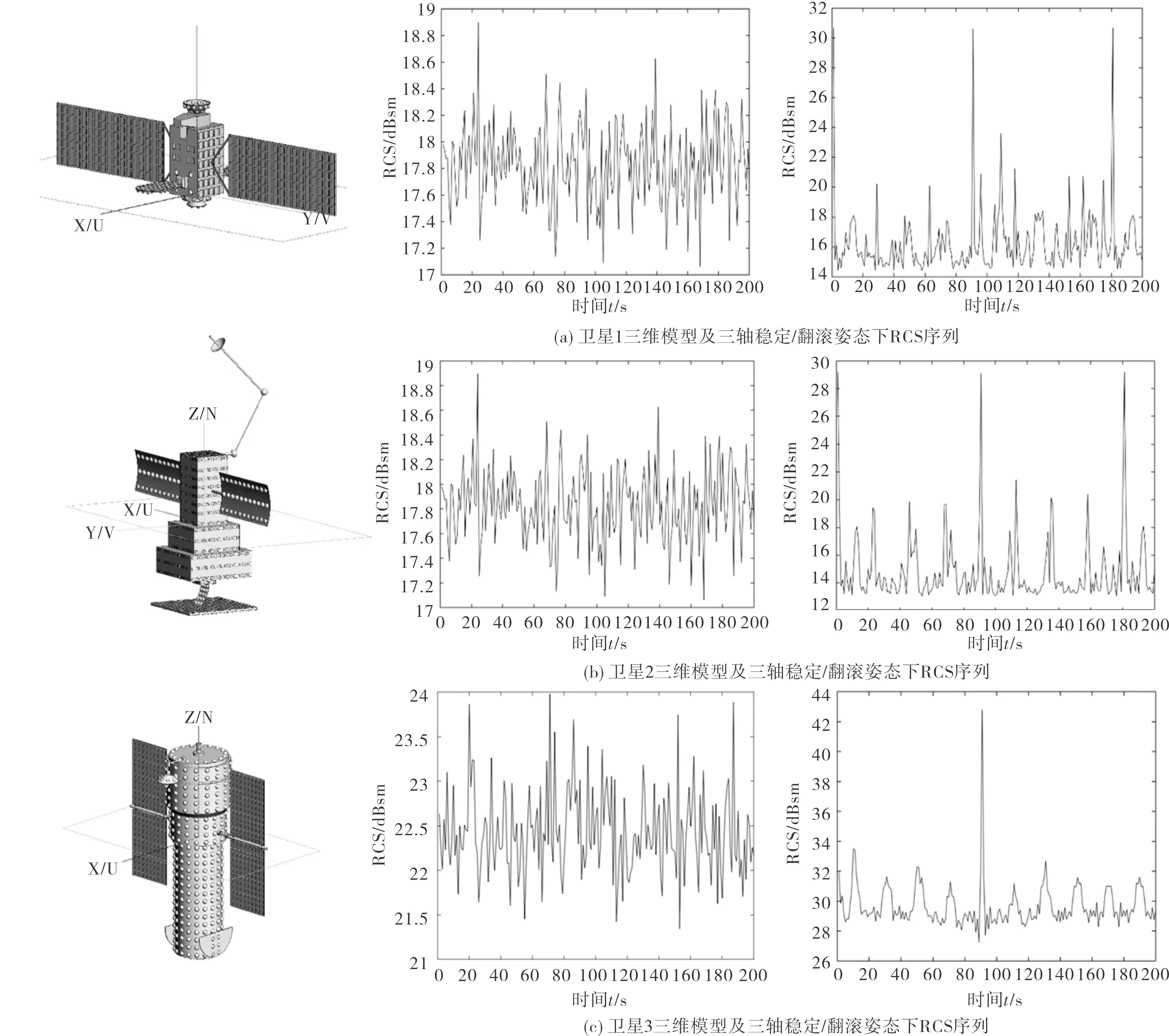
图5 3类卫星FEKO仿真结果Fig.5 FEKO simulation results of three satellites

图6 滑动窗口数据划分Fig.6 Data partition by sliding-window

4 实验结果与分析

4.1 实验环境与参数

为了满足训练对数据样本的需求，共仿真了6 000组窗口RCS数据，按照5∶1划分为训练集与验证集。实验硬件环境基于Intel Core i9-10900 2.8 GHz CPU、NVDIA 3080ti GPU 12 GB、32 GB内存，软件环境基于 Pytorch深度学习框架与Matlab2019a数学分析软件。训练采用自适应矩估计(adaptive moment estimation，Adam)优化器，批样本数为50。训练共迭代1 000轮，学习率为0.000 1，总训练时长为3小时。损失函数采用二值交叉熵(binary cross entropy，BCE)损失函数。

4.2 仿真实验结果与分析

对网络进行1 000轮次的迭代优化，训练集与验证集的损失函数随迭代轮次的变化曲线而变化，如图7(a)所示，验证集的预测准确度迭代轮次的变化曲线如图7(b)所示，训练集在600轮之后损失函数变化趋于稳定，并逐渐收敛趋于0；验证集在200轮后损失函数收敛并趋于0，准确度趋于1，表明网络在训练过程中没有发生欠拟合或过拟合的情况，训练效果较好。

图7 网络训练过程曲线Fig.7 Process curve of network training

测试数据为卫星10圈次的RCS仿真数据，每圈次有30个时间窗口观测数据，一圈次的观测数据为一个测试样本。为了测试网络对不同姿态下目标RCS序列特征的学习能力，采用T分布随机近邻嵌入算法(T-stochastic neighbor embedding, T-SNE)对测试数据的高维特征输出进行可视化降维[9]，如图8所示。

图8 RCS测试数据二维特征分布图Fig.8 Two-dimensional characteristic distribution diagram of RCS test data

为了验证本方法相比于传统算法对目标异常状态检测的有效性，与游程检验法、周期图法以及小波变换方法的各圈次的检测准确率进行了对比，实验结果如表1所列。可以看出，游程检验与小波分解模糊分类的检测方法准确率相对较低。小波分解法的准确率主要在50%上下波动，整体检测效果较差；游程检验的方法准确率最高能达到100%，最低仅为56.67%，稳定性较差；周期图法检测准确率相对较高，平均为82%，表明目标翻滚在RCS序列上表现出一定周期性的时候，该方法比较有效；本文所提方法相较于其他方法准确率最高且波动较小，平均检测准确率相较周期图法提高了17%，表明本方法具有较强的检测性能与稳定性，反映出神经网络在提取目标RCS序列不同尺度的深层次特征以及基于特征进行识别检测方面具有较大优势，一定程度上突破了传统特征提取方法的局限性。

表1 各方法检测准确率

实际应用中，受雷达系统热噪声、环境扰动、标校精度等因素的影响，RCS序列会叠加不同程度的噪声，为了验证所提方法在不同噪声条件下的性能，在测试数据加入5 dB-25 dB信噪比范围的高斯噪声的情况下，各方法检测平均准确度随信噪比而变化，如图9所示，所提方法准确率整体上高于传统方法，当信噪比达到15 dB时，检测准确率能够在90%以上，表明所提方法相较于传统方法具有更强的噪声鲁棒性。

图9 不同信噪比条件下各方法性能曲线图Fig.9 Capability diagram of various methods under different signal to noise ratios

4.3 实测实验结果与分析

利用两个典型三轴稳定与翻滚目标的雷达实测RCS数据，对所提方法的实际检测性能进行分析。为了验证模型的泛化性，采用4.2节FEKO仿真数据训练的模型对实测数据进行检测。实测数据共有200个时间窗口的RCS数据测试样本，每个样本RCS序列长度为100。三轴稳定目标共140个样本，翻滚目标共60个样本，设置时间窗长范围为20-100，对各方法针对不同窗长RCS数据的检测性能进行对比分析，结果如表2所列。检测准确率随窗长的变化而变化，如图10所示可知，随着窗长的缩短，各方法检测性能均有不同程度的下降，但所提方法的检测准确率均超过了90%，整体高于传统方法。

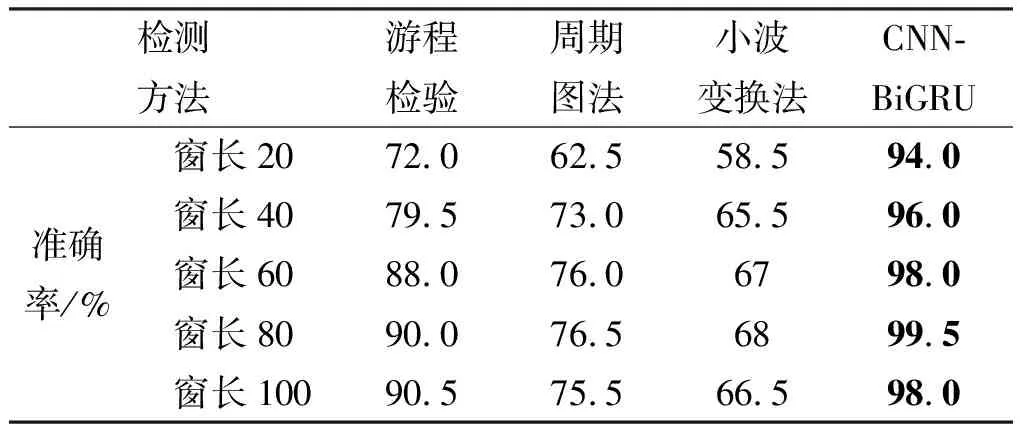
表2 不同窗长条件下各方法检测准确率

图10 不同窗长条件下各方法性能曲线图Fig.10 Capability diagram of various methods under different window lengths

进一步验证所提方法在实际应用中的计算效率，对各方法的运算复杂度进行对比分析。不同窗长条件下各方法耗时如表3所列，内存使用情况(Matlab软件)如表4所列。

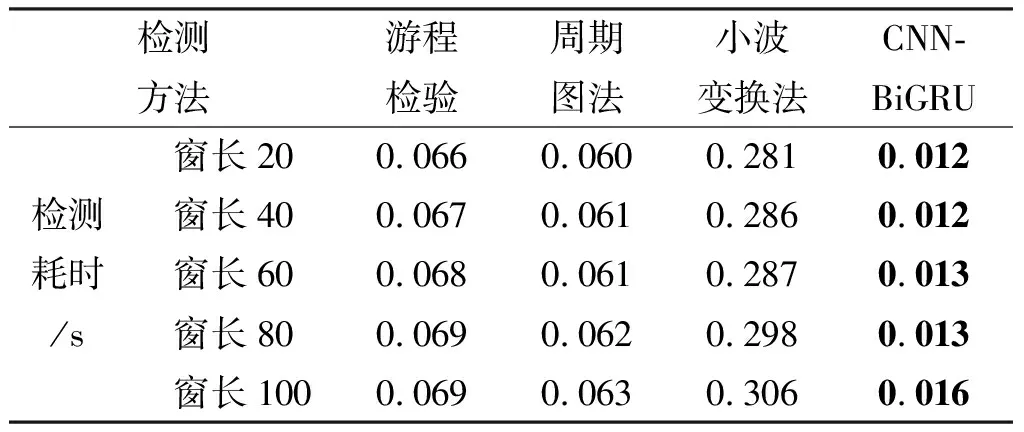
表3 不同窗长条件下各方法检测耗时

表4 不同窗长条件下各方法内存占用

可以看出，随着窗长的增加，各方法检测耗时与内存占用均有不同程度的增加。所提方法整体上相较于其他方法在不同窗长条件下耗时更低，占用内存更少，表明该方法在提升检测性能的同时，有效降低了运算复杂度，更适用于工程应用。

5 结论

针对相控阵雷达体制下RCS数据率低对目标在轨状态检测的影响，本文提出了基于CNN-BiGRU级联网络的RCS异常检测方法，通过结合CNN、BiGRU提取时间序列特征各自的优势，使网络能够学习三轴稳定、翻滚目标RCS序列的时变特征，实现了对目标异常状态的有效检测，避免了复杂的数据预处理与人工特征提取过程。实验结果表明，与传统方法相比，所提方法具有更高的检测准确率及更强的噪声鲁棒性。网络针对非同源的实测数据也具有较高的检测精度，在低数据率条件下检测性能与计算效率明显优于传统方法，表明所提方法更适用于相控阵雷达体制下低数据率RCS的异常检测，具有较大的实际应用价值。