基于ABAQUS的载人潜水器观察窗结构蠕变行为分析
2022-03-19杜青海江海港胡晓康
杜青海,江海港,胡晓康
1 上海海洋大学 深渊科学工程技术研究中心, 上海 201306
2 上海海洋大学 海洋科学学院, 上海 201306
3 上海海洋大学 工程学院, 上海 201306
0 引 言
目前,陆上资源的日益匮乏让全世界的目光开始转向海洋资源。随着对海洋资源的深入研究,各国对海洋的关注重点开始从近浅海逐渐向深远海发展[1],而载人潜水器(HOV)在其中将发挥关键性作用。观察窗是载人潜水器的关键结构之一,其安全性对于人员生命安全以及潜水器性能具有十分重要的作用。相对于金属舱体结构而言,透明玻璃材质观察窗结构的设计更具复杂性和不确定性[2],故国际上的通用规范[3]采取提高安全系数(4~16倍)的方法来确保结构安全。
国内外学者对于观察窗的研究始于上世纪中期,其中最为著名的是美国的Stachiw[4],其毕生都在进行该方面的研究,成果已被写入设计规范[3]并受到国际上相关行业的认可。值得注意的是,Stachiw的研究主要集中在7 000 m潜深范围以内,对于更大的深度,其采取的是增大安全系数按比例进行保守设计的方法。近10年来,我国载人深潜装备随着7 000 m级“蛟龙”号的成功研制,也得到了蓬勃发展,4 500 m级“深海勇士”号以及万米级的“奋斗者”号已相继完成研制。针对载人潜水器的观察窗结构,我国科研人员在结构应力[5]、蠕变特性[6-7]和结构协调性[8]等方面开展了研究。对于全海深大深度观察窗结构,笔者所在课题组通过数值方法,针对观察窗结构规范方法开展了探索性研究[9],指出该设计方法过于保守;随后,又针对观察窗结构进行了优化计算,以寻找最优方案[10]。但对于观察窗的长时间周期和蠕变寿命等问题,尚未开展相关研究。
因此,本文拟采用ABAQUS软件构建锥台型观察窗的有限元计算模型,然后基于窗玻璃材料(丙烯酸塑料材料)的基本性能确定蠕变模型参数,进而分析、验证观察窗结构的蠕变特性,最后,基于有限元蠕变模型计算分析不同加载速度下观察窗结构的蠕变特性及结构性能,为观察窗结构的疲劳寿命研究奠定基础。
1 锥台型观察窗
1.1 观察窗几何结构参数
锥台型观察窗的基本结构参数如下:承受的外载荷P、厚度δ、玻璃低压面(即内侧圆面)直径Di、窗座内口径Df、锥角α,以及厚−径比δ/Di和窗座的悬伸比Di/Df。如图1所示,取锥台型观察窗的内侧圆面为AB面,外侧高压圆面为EF面,选择EF面的圆心O点作为柱坐标系rOz的原点,观察窗轴对称旋转方向,也即锥台观察窗圆面的圆周方向记为θ,AB面的圆心为C点,OF长记为r。
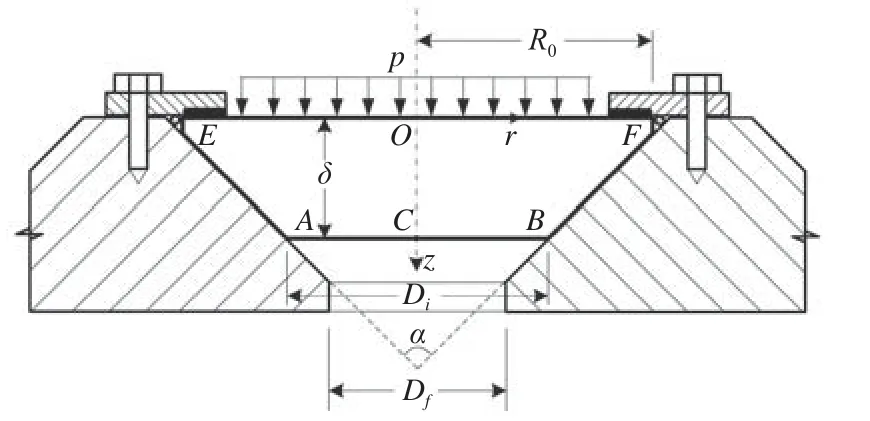
图1 锥台型观察窗的基本结构参数Fig.1 Basic structural parameters of conical observation window
1.2 材料的蠕变特性
由于潜水器观察窗大多数使用丙烯酸塑料(PMMA)[4],这种材料具有比较明显的蠕变特性,能使应力保持在较低水平,且不会导致严重的应力集中现象,有力地推动了观察窗的飞跃式发展。本文锥台型观察窗主要结构材料的机械物理属性[10]如表1所示。

表1 丙烯酸塑料的材料力学参数[10]Table 1 Mechanical parameters of PMMA[10]
图2给出了丙烯酸塑料试件在不同外载荷作用下拉伸后的应变ε随时间t的变化曲线[11],揭示了此窗玻璃材料固有的蠕变特性。
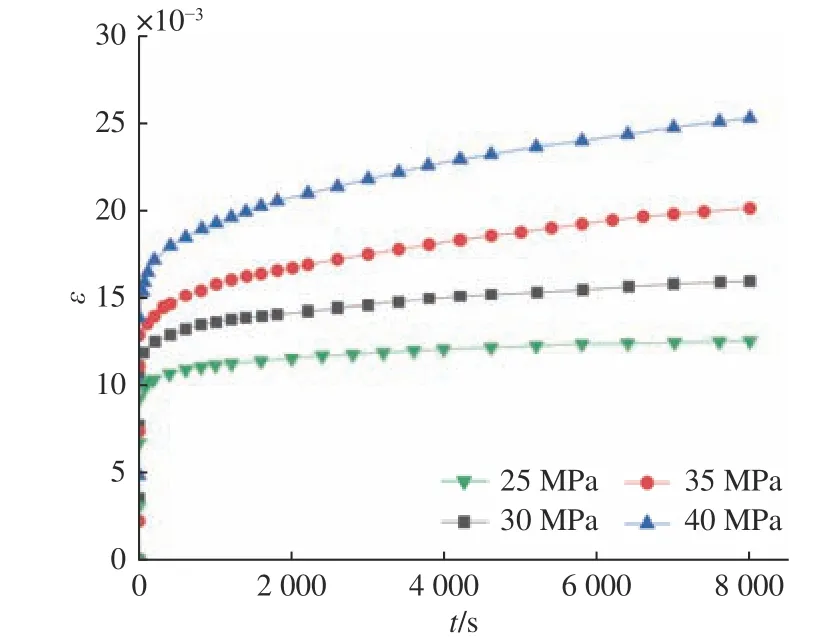
图2 PMMA拉伸试件试验应变随时间的变化曲线[11]Fig.2 Variation of strain level of PMMA with time in tensile specimen experimental test[11]
2 锥台型观察窗蠕变有限元理论
2.1 蠕变理论模型
由于采用传统的ABAQUS线弹性观察窗模型得出的结果忽略了丙烯酸塑料蠕变这一特性,导致计算结果与真实的试验数据间存在较大差异,无法作为普遍的计算方法,因此需要寻找一种能体现蠕变特性的有限元仿真计算方法。为此,本文将在进一步研究观察窗蠕变特性的基础上,采用单步静力−线弹性与多步−非线性相结合的分析步控制方法,同时引入加载和保压的时间,重点得出观察窗的轴向位移、应力和应变等随时间的变化规律。
ABAQUS软件中有3种蠕变模型:双曲正弦模型、应变硬化模型和时效硬化模型,可用来仿真模拟材料的蠕变等特性。其中,恒温与定负载条件下的蠕变特性选择时效硬化模型或应变硬化模型,变温条件下的蠕变特性则使用双曲正弦法则模型。应变硬化的基本思想是:在蠕变发生的全过程中,起到强化作用的主要原因是蠕变变形与时间无任何关系,故其适用于短时间的试验。然而,载人潜水器在工作深度下长时间作业的观察窗结构蠕变特性[6-7]与时间有很大的关系,故观察窗结构蠕变分析可选择时效硬化模型。
时效硬化理论[12]的公式可以表述为:当外界温度一定时,材料的应变ε、应力σ和时间t这3个参数满足的状态函数Φ为:
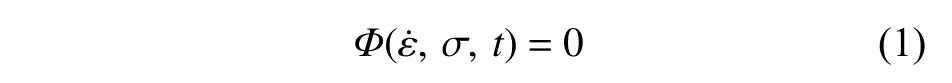
式中,ε˙为应变随时间变化的应变率。
由文献[12]可知,在蠕变发生阶段,影响蠕变的是时效、扩散及恢复这几个参数,且因蠕变曲线在第1、第2阶段具有几何相似的性质,故
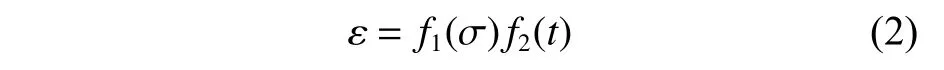
其中,应力函数f1(σ)符合下面的幂函数形式,即
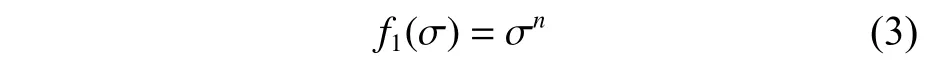
式中,n为应力幂函数的指数参数。
而时间响应函数f2(t)则用Ω(t)函数表示,即

式中,A,m分别为时间幂函数的系数和指数参数。
因此,将式(3)和式(4)代入式(2),可得到时效硬化模型下应变的数学表达式,即
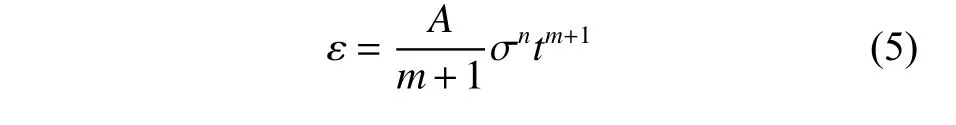
2.2 蠕变模型参数
根据对观察窗结构进行的线弹性数值模拟仿真分析与优化[4,9-10],可知规范规定的锥台型观察窗结构所对应的最大工作压力作用下的整体应力水平基本集中在30~45 MPa之间。鉴此,为得到式(5)中的A,m,n这3个待定系数,根据图2所示的试验数据[11],尽量选择高应力条件下的试验值,即选取30~40 MPa间的材料拉伸蠕变曲线。并且,选择在拉伸试验曲线的两端取点,对拉伸试件试验值与计算值进行对比,如图3(a)和图3(b)所示。由图可见,在这2种取点情况下所得的计算值与试验值相差较大,故应在试验值的中间部分取点,并需满足二者之间误差很小,在此取点情况下的试验值与计算值对比如图3(c)所示。由图可见,拟合出的计算值与试验值基本吻合,证明该组参数有效。具体取点方式如表2所示。

表2 确定参数的取点方式及其解Table 2 Point selecting schemes and solution of determined parameters
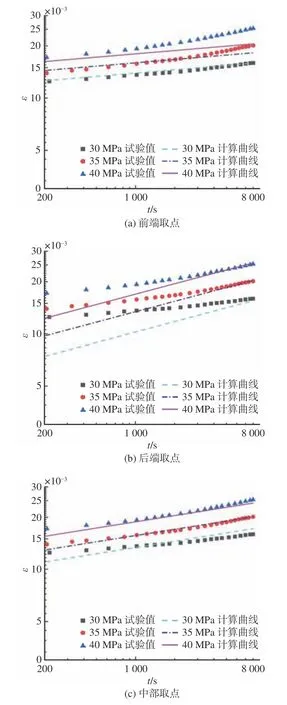
图3 PMMA拉伸试件应变试验值与计算值对比Fig.3 Comparison of strain level between expreimental test and calculation of PMMA tensile specimen
2.3 有限元模型
根据锥台型观察窗结构和均匀静水压力载荷的轴对称性特点,对观察窗结构选取轴对称形式的二维平面模型进行仿真模拟计算。根据模型尺寸,将选取大小合适的CAX4R单元对模型进行网格划分,并设置模型部件之间的接触形式、窗体与窗座之间的摩擦系数和罚函数因子来描述接触[10]。观察窗仿真计算模型的载荷边界约束分布及网格单元划分如图4所示。

图4 ABAQUS有限元模型的载荷边界约束与网格划分Fig.4 Boundary constraints and grid division of finite element model on ABAQUS
2.4 有限元计算方法验证
现有的行业标准ASME PVHO是建立在Stachiw[4]的系列试验模型研究基础之上的,故选取其典型模型尺寸,即主尺度参数。具体如下:Di=25.4 mm,δ/Di= 0.75,1.0,1.25,α=90°。根据真实试验情况将计算压力加载到规范规定[3]的界限压力68.9 MPa,然后保压100 h。
在观察窗结构数值模拟仿真研究[9-10]中,已针对上述尺度的模型验证了线弹性计算环境下,摩擦系数µ=0.05时有限元计算结果随网格粗细变化的准确性及收敛性,得出在该尺度下观察窗和窗座分别采用1 和3 mm的网格比较合适,故此处不再赘述。
运用ABAQUS软件对上述尺度的模型建立几何模型并进行模拟仿真分析,获得加压和保压阶段的应变与变形等,然后将数值模拟仿真所得内侧圆面中心轴向位移fc及其与试验结果的相对误差Δ进行对比分析,结果如图5所示。由图5可见,在前100 h,有限元计算结果与试验结果[4]吻合,误差绝对量在10%以内;在100~1 000 h间,有限元计算结果稍大于试验结果,二者之间的误差保持在11%左右,这说明在此阶段采用数值模拟仿真方法具有保守性。可见,本文仿真计算结果与试验结果较相符。而实际工程应用中保压的时间一般都小于100 h,观察窗体结构因其玻璃材料的黏弹特性,在保压的起始阶段(0~2 h)其结构性能主要由材料的黏弹属性决定[4],故本文将着重选择10~100 h这一阶段进行研究。
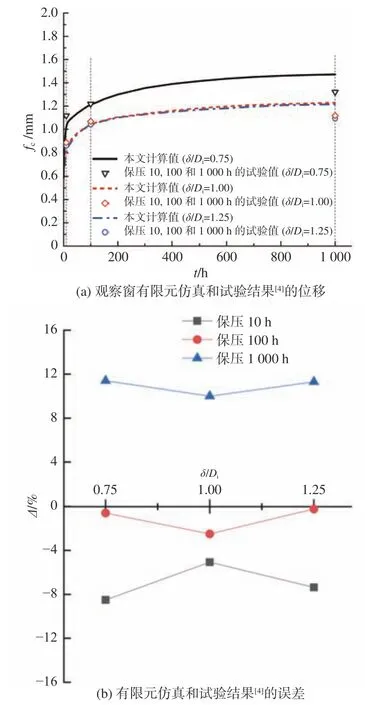
图5 有限元计算结果与试验结果对比Fig.5 Comparison of finite element calculation and experimental test results
3 全海深观察窗结构蠕变分析
3.1 高压作用下的蠕变特性
现有行业规范[3]中的设计方法是通过安全系数法则来确保结构疲劳寿命安全,但却无法揭示长周期载荷下观察窗所具有的蠕变现象,导致计算结果与实测结果存在较大误差[7,9,10],且不利于结构的优化。因此,本文将基于时效硬化模型和试验确定参数的蠕变计算方法深入研究观察窗结构在高压作用下的蠕变等特性。“蛟龙”号观察窗的结构尺寸参数和最大工作压力恰好是规范[3]中方法——曲线设计参数分界[9-10]的典型结构尺寸参数和压力范围,其基本几何结构参数如表3所示。

表3 “蛟龙号”观察窗主尺度参数[5,7]Table 3 Main dimensions of conical observation window of Jiaolong ship[5,7]
利用第2节的数值模拟仿真方法对观察窗结构进行有限元建模和模拟仿真,并在计算过程中分别选择线弹性和时效硬化的蠕变模型。在数值计算过程中,同时采用单步静力−线弹性与多步−非线性相结合的分析步控制的方法加入时间非线性响应。最终,将作用在观察窗模型上的压力加载至71.6 MPa并保压10 h,观察窗结构轴向位移的计算结果,如图6所示。图中,Uz为结构剖面的轴向位移。
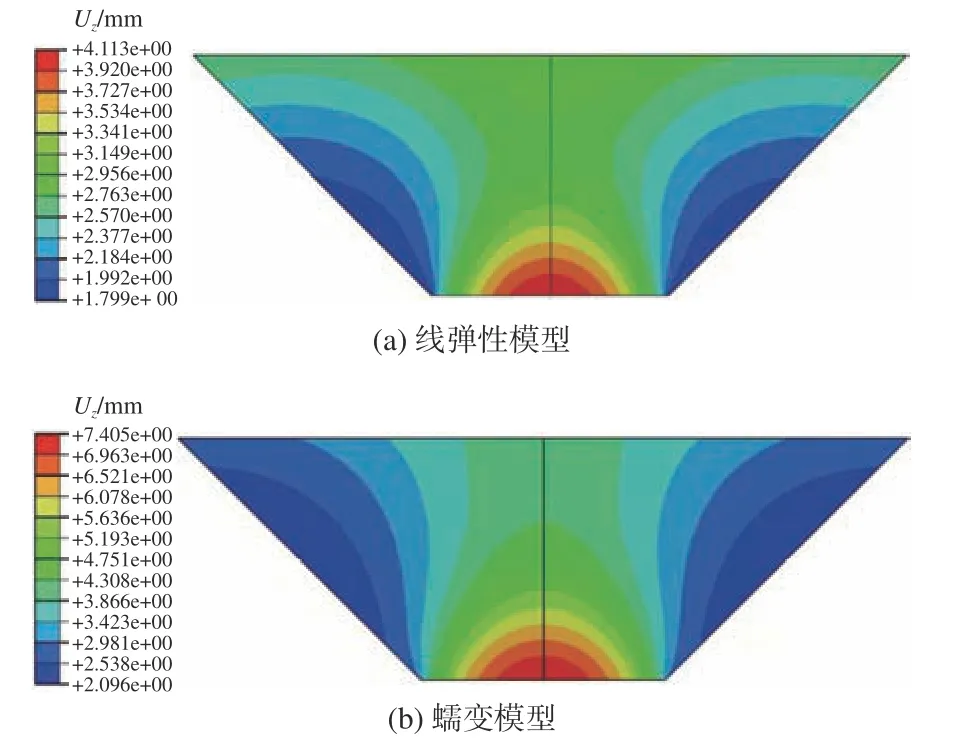
图6 保压10 h后观察窗的轴向位移云图Fig.6 Axial displacement contours of conical observation window after holding pressure for 10 h
图6中给出了观察窗结构在保压10 h后线弹性和蠕变这2种模型下的轴向位移云图,而图7则给出了这2种模型在加载和保压过程中观察窗内侧圆面中心点轴向位移fc随时间的变化曲线。由图7可见,采用线弹性模型计算出的轴向位移在保压阶段无任何改变,而采用蠕变模型计算出的轴向位移fc在保压阶段则是随着时间的增长逐步增大,这直接反映出了观察窗结构蠕变这一特性,与实际结果比较契合。图8进一步展示了最大应变εmax随时间的变化趋势。由图8可见,在保压阶段,采用蠕变模型计算的最大应变随着时间的推移逐渐增大,而采用线弹性模型计算的最大应变在保压阶段则无任何变化,可见观察窗玻璃材料的固有蠕变特性直接导致了观察窗结构在高压下的蠕变特性。
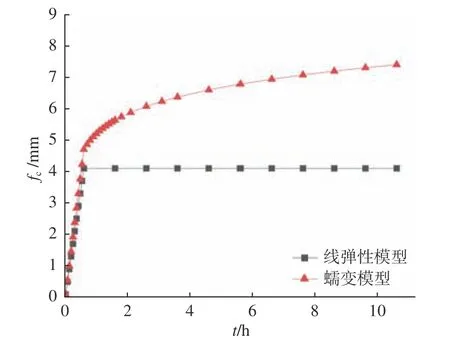
图7 观察窗轴向位移随时间的变化曲线Fig.7 Variation of the axial displacement of conical observation window with time

图8 观察窗最大应变随时间的变化曲线Fig.8 Variation of the maximum strain level of conical observation window with time
根据对深海观察窗结构强度优化的研究[10],发现在主尺度参数下,锥角对锥台型观察窗的结构优化与安全评估具有重要意义。因此,本文选取与表3所示观察窗主尺度参数一致的4组结构模型进行分析,即Di=220 mm,δ/Di=1.0,α=70°,80°,90°和100°,将作用压力加载至71.6 MPa并保压100 h,计算得到4组模型结构的基本力学特性,如图9~图12所示。图中, σ为 最大等效应力,τmax为最大剪应力。
由图9可见,在压力载荷与摩擦系数都相同的情况下,相同厚−径比观察窗内侧圆中心处的轴向位移fc与锥角α成反比;由图10可见,观察窗同一时间处的最大等效应力 σ随着锥角α的增大呈现先增大后减小的趋势;由图11可见,观察窗同一时间的最大剪应力τmax随着锥角α的增大呈增大的趋势;而图12则揭示了观察窗同一时刻的最大应变εmax是随着锥角α的增大呈先增大后减小的规律。综合上述分析,可得锥角α=70°时观察窗尽管在轴向位移方面其数值是4个模型中最大的,但其最大等效应力、最大剪应力和最大应变却是最小的,且应力集中现象不明显。因此,α=70°时的观察窗模型是相对优化的结果,这与线弹性数值模拟优化研究结论[10]一致。
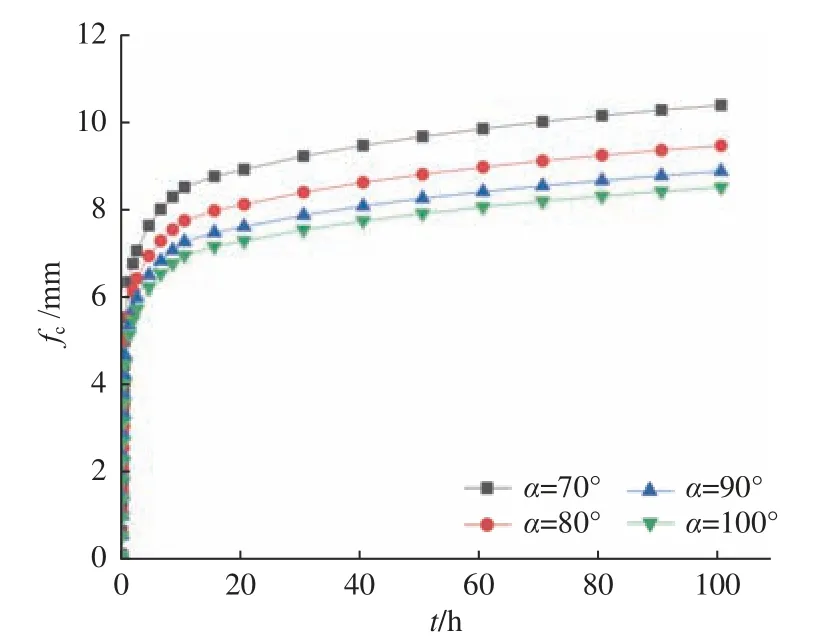
图9 轴向位移随时间的变化趋势Fig.9 The changing trend of axial displacement with time
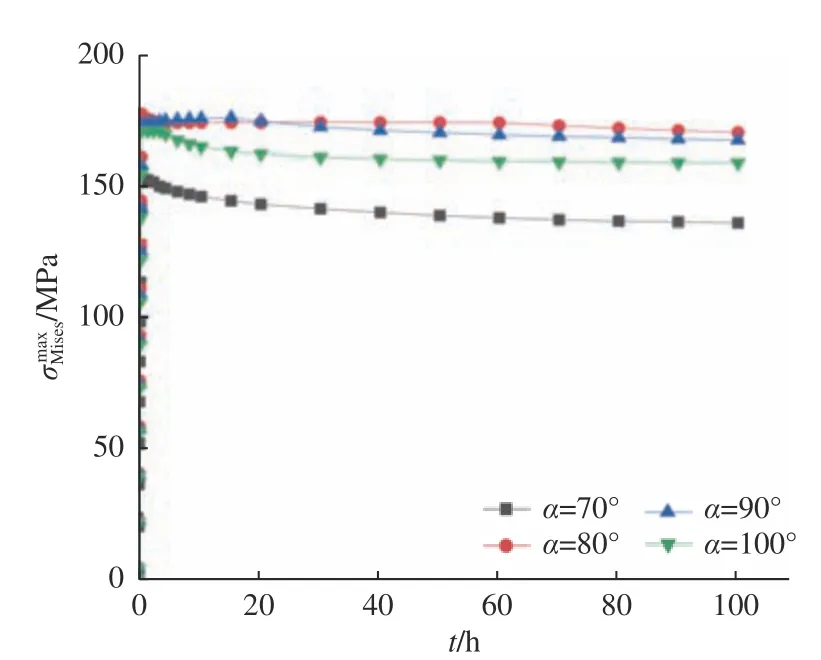
图10 最大等效应力随时间的变化趋势Fig.10 The changing trend of maximum equivalent stress with time
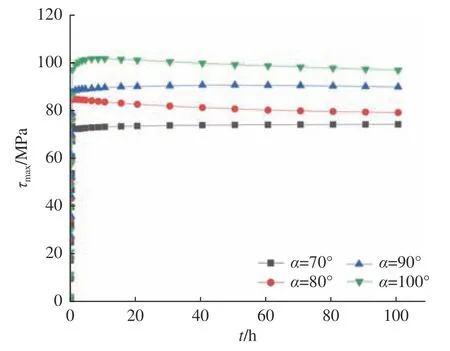
图11 最大剪应力随时间的变化趋势Fig.11 The changing trend of maximum shear stress with time
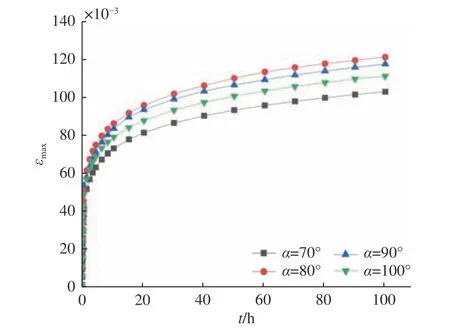
图12 最大应变随时间的变化趋势Fig.12 The changing trend of maximum strain with time
3.2 不同加载速度下的蠕变特性
经过大量的仿真计算,发现不同的加载(下潜)速度对观察窗的位移、应变及最大等效应力等输出值均有影响,会影响结构的蠕变特性。
为便于研究,针对3.1节中优化结果,设Di为固定值220 mm,α=70°,δ/Di=1.0,摩擦系数µ=0.05,采取3种不同的加载速度,即0.67,2和6 MPa/min,然后将观察窗模型的作用压力P加载至71.6 MPa并保压100 h,最后研究采取不同加载速度时对观察窗结构基本力学性能的影响。
图13和图14给出了加载和保压过程中观察窗结构的位移和最大应变特性。由图可见,在将作用压力加载至71.6 MPa的过程中,3种加载速度下的位移和应变值相差无几,只是随着加载时间的缩短,二者略有降低;而在保压阶段二者差距却十分明显,尽管保压时间相同,但随着加载时间的增加,位移和最大应变在保压阶段增长的幅度反而降低了。图15显示出在整个加载过程中不同加载速度下的最大等效应力值几乎一致,其变化主要体现在保压阶段,即随着加载时间的增大,最大等效应力的降幅在减小。由图15可见,在相同的长时间保压作用下,延长加载时间相对缩短加载时间而言,与正常加载速度(例如2 MPa/min)相比,观察窗模型结构计算的等效应力变化幅度受到的影响较大。综上所述,压力加载速度不宜过快,否则不利于高压保压阶段的结构蠕变应变及位移释放。
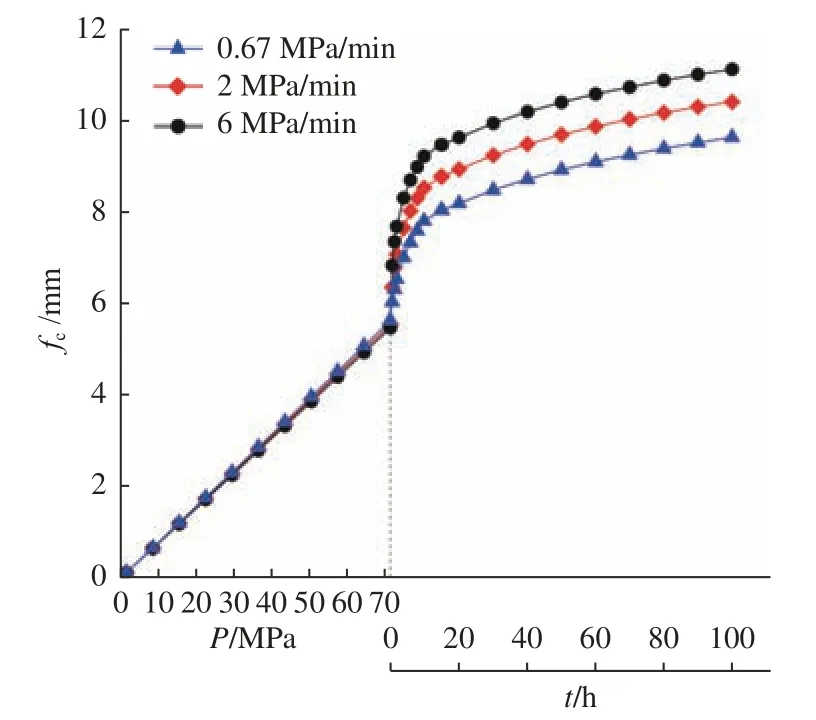
图13 不同加载速度下位移的变化曲线Fig.13 Variation of displacement under different loading speeds
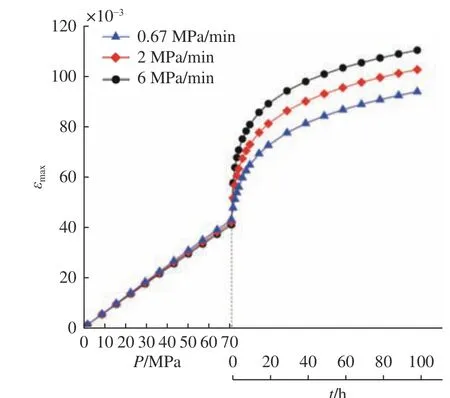
图14 不同加载速度下最大应变的变化曲线Fig.14 Variation of maximum strain under different loading speeds
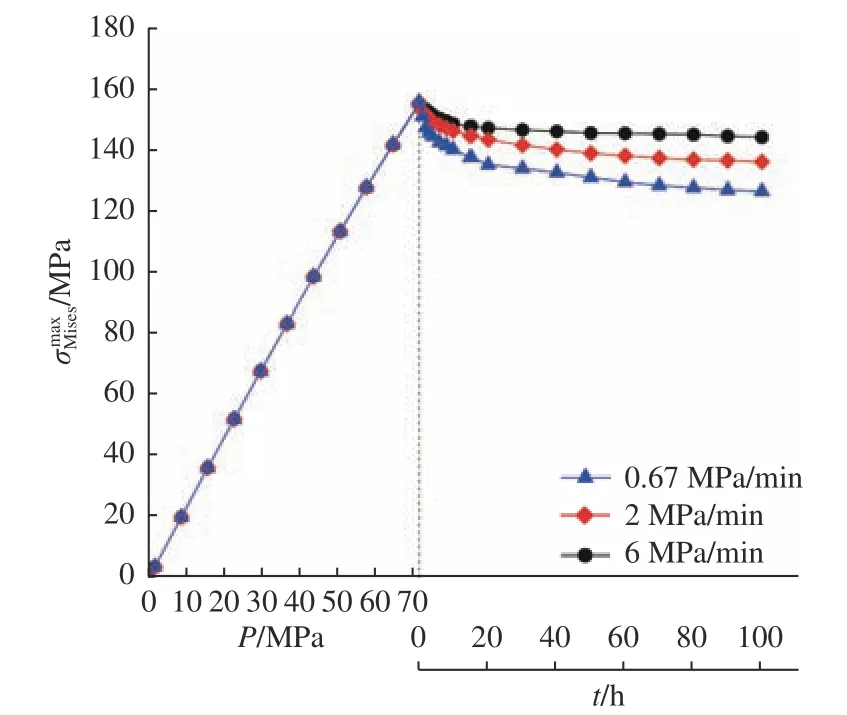
图15 不同加载速度下最大等效应力的变化规律Fig.15 Variation law of the maximum equivalent stress under different loading speeds
3.3 观察窗蠕变特性下的结构强度
为了更好地研究观察窗材料蠕变特性下其强度的力学结构属性,需进一步分析观察窗在长时间保压作用下的结构强度特性,这对观察窗的疲劳寿命分析来说意义重大。因此,选取前述优化的观察窗结构主尺度参数,即Di=220 mm,δ/Di=1.0,α=70°,再按2 MPa/min加载速度将作用压力加载至71.6 MPa,并保压100 h。
图16(a)所示为保压后观察窗上表面(EF面)在3个方向的应变曲线。由图可见,在EF面中心附近存在高应变集中区域,数值上呈现从中心向四周递减的趋势,图中虚线范围所表示的区域随着外部加载的不断增大,出现了“凹坑”情况[4]。图16(b)所示为内侧圆面(AB面)在3个方向(即图1所示柱坐标系下)的应变曲线。由图可见,内侧圆面在边缘处易出现因几何结构和应变突变所导致的裂纹等。图中 ,εr,εθ和 εz分别为3个坐标轴方向上的主应变。

图16 观察窗外/内表面的应变曲线Fig.16 The strain distribution of outside/inside surface of conical observation window
图17所示为观察窗保压后的3/4立体应变云图。从图中可以直观地看出,EF面中心O点附近3个应变分量的绝对值明显高于四周,这也进一步揭示了在高压下观察窗上表面会出现“凹坑”的破损失效现象。
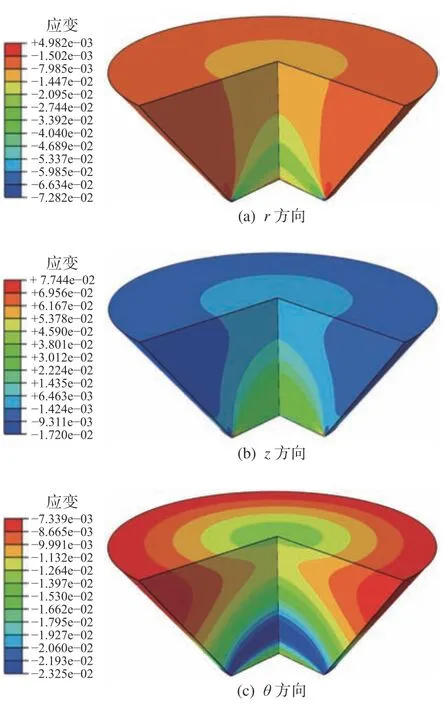
图17 观察窗结构的应变云图Fig.17 The strain contours of conical observation window structure
图18给出了在保压过程中,在0,10,100 h这3个时刻观察窗中心轴线OC上沿z轴3个方向的应变变化情况,图中纵坐标为轴线OC位置坐标z与厚度δ的比值,横坐标为应变值大小。从图中可以清晰地看出,虚线区域内的应变量会随着保压时间的增加而持续增加,相比其他中心轴线OC上区域,该区域受到的应变突变更严重,也更容易出现损伤破坏。
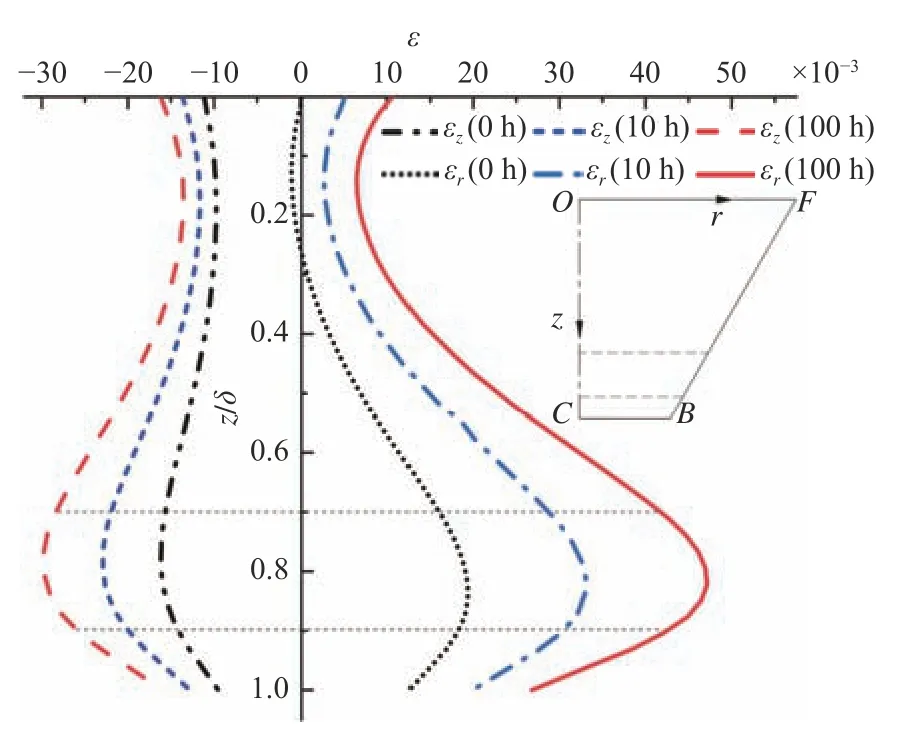
图18 观察窗中心轴线OC的应变曲线Fig.18 The strain distribution along OC at the center axis of conical observation window
4 结 论
本文基于丙烯酸塑料材料的蠕变特性,采用ABAQUS软件对锥台型观察窗结构进行了数值模拟仿真计算,并通过时效硬化模型对材料和观察窗结构的蠕变特性展开了分析,主要得到如下结论:
1) 基于ABAQUS软件,构建了用于评估锥台型观察窗在长周期载荷下材料与结构蠕变特性的可靠数值方法。
2) 观察窗结构有限元线弹性模型与蠕变模型的比较分析,以及笔者所在课题组之前对蠕变模型与典型参数模型试验的对比分析表明,蠕变模型下的计算结果更符合试验情况。通过多参数优化计算分析观察窗结构的蠕变特性,并在特定主尺度参数下优化对比锥角对结构性能的影响,结果显示锥角α=70°时观察窗结构的蠕变特性更优。
3) 不同加载(下潜)速度下观察窗的蠕变强度研究显示,为避免蠕变特性下的结构损伤,不宜采取过快的加载速度。
本文针对观察窗结构的蠕变特性分析可为今后观察窗结构的优化设计提供参考。
