基于伴随方法的舰船推进器优化设计

2022-03-19王睿熊鹰

中国舰船研究 2022年1期

王睿，熊鹰

1 中国人民解放军91404部队，河北秦皇岛 066001

2 海军工程大学舰船与海洋学院，湖北武汉 430033

0 引言

目前，船舶螺旋桨的优化设计大多基于智能优化算法[1-4]，但其优化效率与设计变量的数目息息相关。对于多目标、多参数的优化设计问题，智能优化算法的效率往往比较低。因此，智能优化算法应用于螺旋桨的优化设计需要耗费大量的计算时间[5-8]。为了解决好此矛盾，将空气动力学中迅速发展起来的伴随方法引入到螺旋桨的优化设计中[9]。伴随方法通过伴随方程实现敏感导数的计算，得到目标函数与设计变量的敏感导数关系，具有极高的优化设计效率[10-11]。伴随方法最早于1974年应用于流体力学问题[12]，随后在机翼、飞行器及涡轮机械的优化设计方面得到广泛应用[13-15]。尽管伴随方法的研究已逐渐深入，但在船舶螺旋桨的优化设计中还未涉及。

为了探究伴随方法在螺旋桨优化设计的实际效果，本文将开展基于面元法的伴随方法研究，详细探讨伴随方法应用于螺旋桨优化设计中的求解方程和数值处理，以为螺旋桨的优化设计建立高效可行的数值方法。

1 基于面元法建立伴随方程

势流方法和黏性流方法均可应用于分析船舶螺旋桨水动力问题。其中，基于势流的面元法未对几何模型作任何假设，计算结果比较精确；而黏性流方法大多基于商用软件，难以进行数值程序的修改和扩充，故而选择基于面元法建立伴随方程。面元法通过在物面上布置奇点来模拟流体流经桨叶的运动状态。通过拉普拉斯方程和格林函数得到螺旋桨表面任一场点p的速度势为[16-17]

式中：q为控制点；SB为螺旋桨的边界；SW为螺旋桨尾涡面的边界；nq为控制点外法向；Rpq为场点与控制点之间的距离；φp与 φq分别为场点与控制点的速度势； Δφq为螺旋桨尾涡面偶极子强度。

针对螺旋桨水动力性能的优化，目标函数I可以表示为流动特征量U和设计变量x之间的函数。由于面元法计算中，通过等压库塔条件，尾涡面速度势与桨叶面速度势可以相互求解，因此，选择尾涡面速度势或者桨叶面速度势作为流动特征量是可以等效的，在这里流动特征量选为尾涡面速度势Δφ，设计变量x即为螺旋桨的几何参数，故目标函数可以写为

目标函数可以是螺旋桨的推力、扭矩、最大负压系数和噪声等；设计变量x可以是弦长、螺距和侧斜角度等。通过等压库塔条件，可建立速度势与几何变量间的关系：

式中：pU为随边叶背压力；pL为随边叶面压力；压差Δp可通过雅克比矩阵建立与Δφ间的关系。引入伴随变量λ，则敏感导数的求解式可写为：

其中，λT满足式（5）：

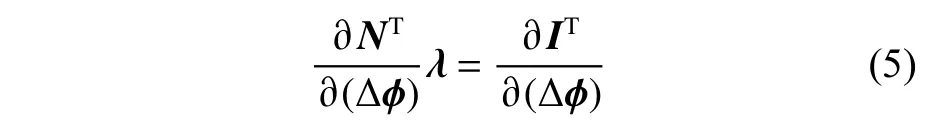
式（5）即为伴随方程。求解完成控制方程式（1）后，基于式（3），微小改变x和Δφ，即得到N与x，Δφ间的偏导数。基于式（1），微小改变x和Δφ ，即得到I与x，Δφ之间的偏导数。于是，求解一次伴随方程式（5），得到伴随变量λ的值，代入敏感导数求解式（4）即得到了敏感导数结果。可以看出，建立伴随方程后，敏感导数的求解不再需要重复求解控制方程，只需要求解一次控制方程式（1）和一次伴随方程式（5），即可完成敏感导数的求解，这对于设计变量较多的优化问题，具有极大优势。

2 敏感导数计算结果对比

为检验伴随方法的敏感导数计算精度，以DTMB4381螺旋桨为对象，运用伴随方法和传统方法分别计算推力、扭矩、效率与螺距分布、拱弧分布之间的敏感导数，并对比计算结果。传统的敏感导数计算是每改变一次设计变量x，求解一次控制方程式（1），得到ΔI与 Δx的比值，即为敏感导数。若采用中心差分的方法，则每改变一次设计变量x，需要求解2次控制方程。在本次计算中，采用的面元法计算结果与实验值对比具有较好的一致性[18]，伴随方法及传统方法计算敏感导数均采用中心差分的数值处理，计算对比结果如图1所示。图1中：KT为推力系数；KQ为扭矩系数；η0为敞水效率；P/D为螺距比；fmax/C为拱弧比弦长；r/R为螺旋桨径向位置。以dKT/d(P/D)表示推力系数与螺距比之间的敏感导数关系，其他敏感导数的意义与此式类似。

图1 DTMB 4381桨螺距及拱弧敏感导数对比Fig.1 Sensitive derivative comparison of pitch ratio and camber ratio of DTMB 4381 propeller

图1给出了敏感导数沿螺旋桨径向分布，对比结果可知，伴随方法及传统方法的敏感导数计算结果具有较好的一致性，但在叶梢位置处的有一定差别。分析认为，面元法的计算模型在叶梢位置处的精度有限，微小改变螺旋桨几何时，敏感导数计算结果存在一定的差值，但变化曲线的突变点并不影响径向参数对螺旋桨性能影响的变化方向，若要消除叶梢处的曲线突变点，可通过调整叶梢处网格疏密及径向参数的变化值大小来处理，限于本文研究的主题，在此不再详细探讨。进一步分析可知，伴随方法在敏感导数计算中，需同时对Δφ与x的数值进行微小扰动，可在一定范围内平衡数值误差，从而使计算结果更加稳定，对几何参数的改变更加敏感。而传统方法只改变几何变量x，敏感导数计算结果对几何参数的敏感性较差。对比两者敏感导数的计算时间，就本文计算中选取的10个径向位置而言，伴随方法的敏感导数计算时间约为传统求解方法的1/10。因此，伴随方法的效率优势明显，尤其对于设计变量较多的状况，计算时间会大大减少。

3 螺旋桨优化设计

伴随方法求解敏感导数的最终目的是指导螺旋桨的设计，根据敏感导数结果迅速找到几何参数与螺旋桨性能之间的定量关系。选择文献[18]的螺旋桨HG01作为研究对象，文献[18]基于ISIGHT平台，结合实验设计方法和粒子群算法对螺旋桨进行了优化设计，设计过程中保持推力不变，提高螺旋桨的效率和最大负压系数。研究中首先对此螺旋桨进行敏感导数的分析，因文献[18]只改变螺距比及拱弧比，为了对比研究，本文也只对螺距比及拱弧比进行优化。敏感导数计算结果如图2所示。

图2 HG01桨径向参数敏感导数对比结果Fig.2 Comparison of sensitive derivative of HG01 propeller's radial parameters

从图2可以看出，螺距由叶根到叶梢，对螺旋桨的推力、扭矩的影响效果逐渐变大，而对效率的影响效果是先增大后减小。由叶根到叶梢，拱弧对于螺旋桨的推力、扭矩及效率的影响效果均逐渐增大。但螺距对效率的影响是负相关的，拱弧对效率的影响呈正相关。根据螺距和拱弧对推力、扭矩以及效率的影响，选择适当的变化方式，改变螺旋桨螺距及拱弧的径向分布。由于螺距在0.7R处，对效率的影响最大，靠近叶根与叶梢对效率的影响逐渐变小，且呈负相关。为了维持推力不变，同时提高效率和改善空泡性能。选择减小螺距，增大拱弧。螺距在0.7R处减小幅度最大，靠近叶根及叶梢端的减小幅度逐渐减小。拱弧由叶根到叶梢均增大，从叶根到叶梢增大的幅度逐渐变大。

根据优化过程中以敏感导数的定量结果作为参考，按照各个几何参数的1%进行逐步迭代修正。先调整螺旋桨的径向几何参数，再调整螺旋桨叶剖面几何，来达到改善螺旋桨空泡性能的目的，同时需要满足螺旋桨的敞水性能保持不变。如式（6）所示，下标加0表示优化前数值。

式中，自变量为螺旋桨径向参数和尾涡面速度势径向值。

最终优化得到的螺旋桨螺距及拱弧的对比如图3所示。另外，基于ISIGHT优化平台的粒子群方法（PSO）得到的螺距及拱弧对比如图4所示。

图3 伴随方法优化前后几何参数对比结果Fig.3 Comparison of parameters before and after optimization with the adjoint method

图4 ISIGHT优化平台的粒子群算法优化前后几何参数对比结果Fig.4 Comparison of parameters before and after optimization with the PSO algorithm of ISIGHT

由图3和图4可以看出，伴随方法与粒子群优化方法对于螺旋桨螺距及拱弧的改变方式是完全不同的，但根据敏感导数分析结果可知，粒子群优化方法对螺旋桨螺距和拱弧的改变方式也是可行的途径之一，但不是提高效率、优化空泡性能及同时保持推力不变的最佳途径。为了对比伴随方法及粒子群方法的优化效果，对伴随方法及粒子群算法优化得到的推力、扭矩系数和敞水效率以及最大负压系数进行了对比，对比结果如表1所示。表中“+”表示增加，“−”表示降低。计算用的是同一台计算机，CPU为4核Intel Core 2 Quad CPU Q6600 @ 2.4 GHz。