跨域无人平台水面垂直起飞动态特性数值模拟

邱磊，郑巢生

1 海装重大专项装备项目管理中心，北京 100071

2 中国船舶科学研究中心 船舶振动噪声重点实验室，江苏 无锡 214082

0 引 言

水下−空中跨域两栖无人平台结合了飞机、水面船和水下航行器的优点，灵活、机动且能自主运行，既可在水下潜航、协同作业并在必要时提供中继服务，也可贴近海面飞行，执行快速搜索、运输及中转等任务[1]。

近年来，国内外越来越多的学者对跨域无人平台进行了相关研究，同时，随着计算机应用技术的发展，数值模拟作为一种有效的研究手段，也越来越多地被应用到跨域无人平台研究领域。吝科等[2]采用数值模拟手段，针对升力型航行器开展了飞行时的空气动力学和潜航时的水动力学特性研究。齐赞强[3]针对设计的一种新构型倾转四旋翼无人机，开展了倾转过渡状态下螺旋桨对机身、机翼和尾翼的干扰数值模拟研究。吴江等[4]采用CFD软件，对某型倾转旋翼机的螺旋桨拉力及功率等性能进行了计算。邓见等[5]采用数值模拟方法研究了仿飞鱼跨介质无人平台在水下游动和水面滑行阶段的水动力性能，解释了飞鱼滑跑阶段的合理性。廖保全等[6]采用Fluent软件，针对一种可改变外形的水−空跨介质航行器进行了空中和水中2种外形的气动力/水动力特性数值模拟，结果表明，通过改变外形航行器能够同时满足水下航行和空中飞行的要求。魏洪亮等[7]提出了水下发射航行体跨介质动态载荷预报方法，通过模拟出水过程中航行体逐步由水到气的跨介质卸载作用，获得了航行体轴向速度、俯仰角度、俯仰角速度和弯矩等关键参数随时间的变化规律，模拟结果显示与试验数据吻合较好。谭骏怡等[8]针对一种可变体的水下构型，采用Fluent软件模拟了该构型在典型工况下的出水过程，结果表明，航行器倾斜跨越水−空界面时两侧的流场和载荷会出现不对称的剧烈变化，俯仰角越大，在水下的部分其流场受动范围越小，跨越出水部分受影响越大；与零攻角出水相比，航行器带攻角倾斜出水会导致表面所受流体作用力出现高频率、大幅度的反向震荡，影响出水的稳定性。杜特专等[9]针对跨介质航行器三角型截面舵翼，采用Fluent软件对其运动过程中的空化流动与结构振动耦合进行模拟，分析了不同攻角下的空泡形态以及舵翼与空化流动的相互作用，结果表明，当来流攻角为2°～6°时，航行器及舵翼几乎被包在超空泡内部；当来流攻角为8°时，舵翼的自由端会穿透空泡界面，使其所受水动力比小攻角条件下的大一个量级，振动特征也更加复杂。贾力平等[10]采用基于自由液面捕捉法的FINE/Marine软件，模拟分析了DLR-F4飞机模型在水上迫降过程中的流场和水动力特性，并与已有实验结果进行了对比，结果显示该模拟方法可以很好地预测跨介质航行器的运动特性和水动力特性。谭骏怡等[11]针对一种特殊的双层半环形闭合翼构型，采用Fluent软件对该构型跨越水−空介质后变体过程中的不同状态气动力进行了数值模拟，结果表明，机翼回收过程中的气动参数要大于定常状态，展开过程中的气动参数则小于定常状态，且变体速率越大，非定常效应越明显，而产生这种差异的原因来自于流场迟滞的影响。

综上所述，目前跨域无人平台的数值模拟研究大多聚焦于水下水动力或空中气动力性能，较少考虑平台自身在流体作用下的自由运动，且由于跨域无人平台作业任务多样，导致其运动模态也复杂多变，其中，作为多模态运动的重要环节——无人平台从水面到空中的跨越过程，对于无人平台的跨域功能性和安全性尤为重要，相关的跨域过程动态特性数值模拟研究相对较少。为此，本文拟采用黏流CFD方法结合重叠网格技术和多自由度DFBI运动模型，针对跨域无人平台从水面垂直起飞至空中跨域过程的动态特性开展数值模拟研究，分析其运动及动力学特性，为后续跨域无人平台优化设计及控制提供有力的评估手段。

1 研究对象及数值模拟方法

1.1 研究对象

本文选取一种跨域无人平台作为研究对象，如图1所示。该平台总长L=3.0 m，翼展长B=2.8 m。无人平台在空中飞行时自身重力通过两侧机翼产生的升力克服，飞行姿态通过垂直尾翼与水平尾翼的配合来控制，当无人平台在水面起飞或降落时，推进器竖直向上产生升力，以克服无人平台起飞或降落时的重力。本文主要开展无人平台从水面垂直起飞至空中这一跨域过程的动态特性数值模拟研究。

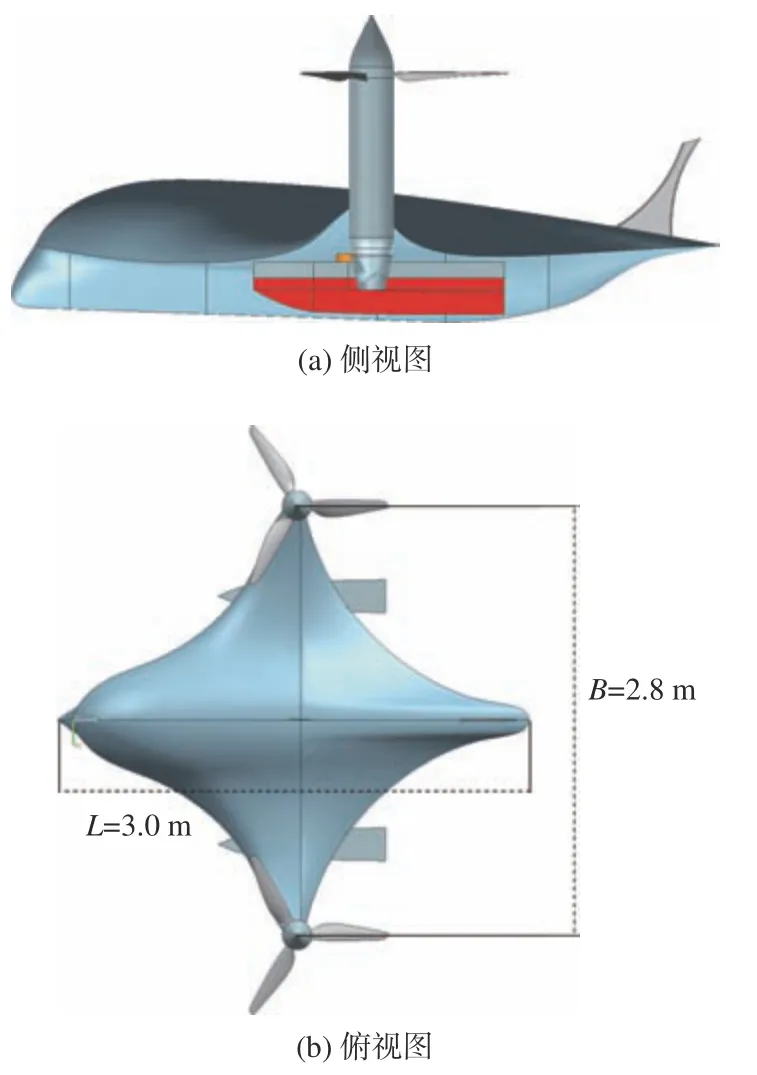
图1 一种跨域无人平台Fig.1 A trans-media unmanned vehicle

1.2 数值方法

1.2.1 控制方程

本文中无人平台在初始时刻平稳地浮于水面，此时需考虑自由液面的影响，可选用流体体积法（VOF）模拟自由面的水、气两相流，即流动中包含水、空气2种流体，其中水的密度ρwater=998.2 kg/m3，空气的密度ρair=1.225 kg/m3。定义空气在计算网格上的空间占比为α， 当α=1时网格内全部为空气，α=0时网格内全部为水，当0<α<1时网格内既包含气体，同时也包含水。

水、气两相流的密度 ρ和 黏性 µ为空气和水的线性组合：

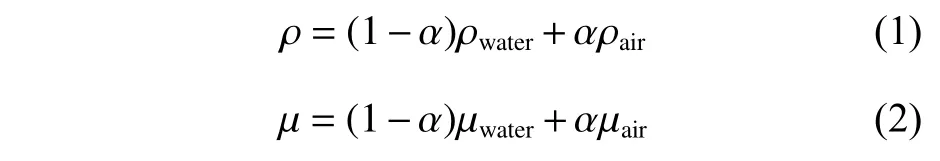
为了简化问题，鉴于流速比较低，假定空气和水都为不可压缩流体。流动的控制方程如下所示。

不可压缩方程：

式中：V为速度矢量；p为流体压力；g为重力加速度。

湍流模型选取SSTk-ω模型[12]，运动模型采用六自由度DFBI模型[13]。

1.2.2 数值求解方法

流动的数值求解使用有限体积法。连续性方程和动量守恒方程中的对流项离散使用二阶迎风格式，扩散项使用二阶中心差分格式，流场中的物理量梯度计算使用基于单元的Green-Gauss方法。离散方程求解利用SIMPLE方法和Gauss-Seidel迭代，同时，求解过程中使用多重网格技术加速迭代的收敛。压力和速度计算松驰因子分别取0.2和0.5。计算采用隐式非定常方法，计算时间步长选取螺旋桨旋转3°所用的时间。

1.2.3 初始边界条件

无人平台计算域如图2所示。由于无人平台为左右对称布局，在不考虑左、右侧向运动及横滚的情况下，为了减少计算量，采用对称边界取一半进行计算。为研究无人平台在水面起飞时的运动及动力特性，采用重叠网格技术结合多自由度DFBI模型方法，计算中不考虑风、浪、流对无人平台起飞特性的影响，入口速度定义为0 m/s。自由面初始位置为排水体积为60 kg时的吃水深度。

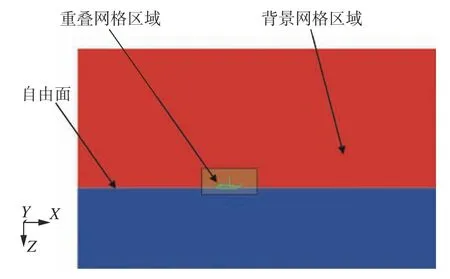
图2 数值模拟计算域Fig.2 Computational domain for numerical simulation

1.2.4 计算网格

采用切割体单元网格对计算域进行网格划分，网格总数为432万，其中背景网格160万，重叠区域网格104万，空气螺旋桨旋转区域网格168万；对自由面、平台表面、螺旋桨表面及附近，以及背景网格中原理样机的运动路径进行网格加密，如图3和图4所示。

图3 计算域总体网格Fig.3 Total grids of computational domain

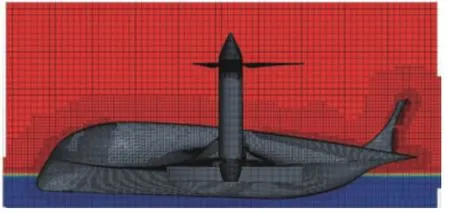
图4 重叠区域网格Fig.4 Local grids of overset zone

2 数值模拟结果及分析

2.1 数值方法验证

在开始跨域无人平台水面垂直起飞动态特性模拟之前，需要开展数值方法验证，特别是空气螺旋桨气动力数值计算方法的验证。

空气螺旋桨在市场上有多种产品可供选型，并且都有厂商提供的拉力试验测试数据。本文首先选用了某型二叶商用空气螺旋桨，如图5所示，该螺旋桨桨叶直径0.660 4 m。由于没有该桨的详细几何型值，先对所选购的空气螺旋桨进行了几何逆向扫描，获得了精确的桨叶几何模型，然后，针对该几何模型进行了数值建模和气动力特性数值计算分析，其中空气螺旋桨表面网格如图6所示。计算中，采用的是SSTk-ω湍流模型结合非定常滑移网格方法。表1所示为厂商提供的二叶商用空气螺旋桨拉力试验数据和气动力数值计算结果比较。

图5 二叶商用空气螺旋桨Fig.5 The two-bladed commercial air propeller

图6 空气螺旋桨气动力计算网格Fig.6 The surface grids of air propeller for aerodynamic performance calculation

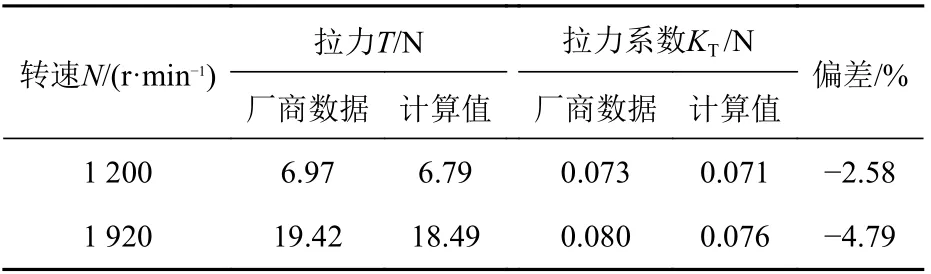
表1 某型二叶商用空气螺旋桨性能试验值与数值计算值Table 1 The experimental and numerical values of aerodynamic performance of a two-bladed commercial air propeller

从表1中可以看出，计算值与厂商数据吻合较好，说明目前的数值预报方法可以较好地模拟空气螺旋桨的气动力特性，通过数值计算，能够作为空气螺旋桨气动力性能评估的依据。

2.2 计算工况

在开始水面起飞跨域过程的动态数值模拟之前，针对设计的三叶空气螺旋桨进行了气动力特性计算研究，其中桨叶直径D=1.2 m。为了提供单桨294 N的拉力，使无人平台以1 m/s的速度上升，计算得到空气螺旋桨不同转速下的拉力与扭矩如表2所示。

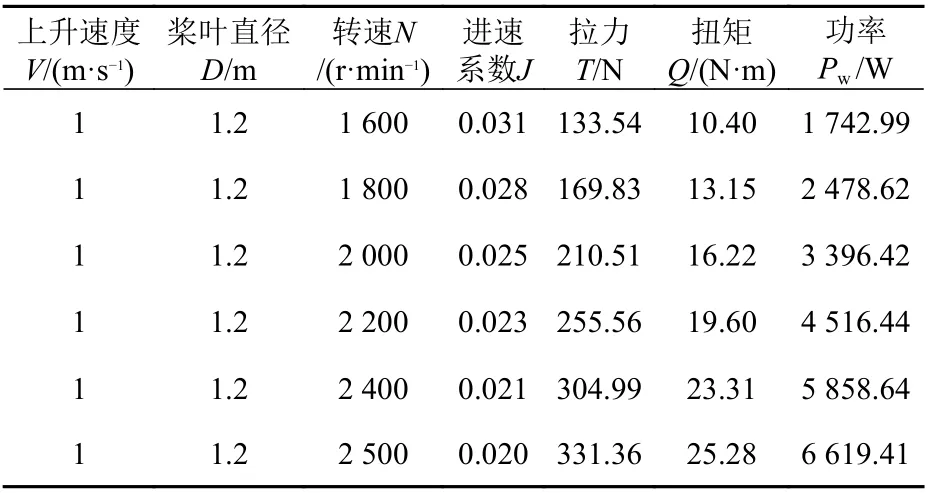
表2 不同转速下单个三叶空气螺旋桨的拉力、扭矩与功率Table 2 The pull force, torque and power of a three-bladed air propeller at different rotation speeds

为满足294 N的拉力，通过插值计算，初步判断三叶空气螺旋桨桨叶直径D=1.2 m时转速需达到2 352 r/min。但这仅是针对单个空气螺旋桨在敞开环境中的评估结果，没有考虑空气螺旋桨与无人平台之间的相互干扰。因此，本文后续计算中，将考虑空气螺旋桨与无人平台之间的相互干扰，并放开无人平台的运动自由度，模拟无人平台从水面静止状态到起飞的动态过程。

2.3 计算结果与分析

计算时，首先选取空气螺旋桨的转速为2 352 r/min，针对无人平台起飞过程中的运动特性与动力学特性进行计算，其自由度示意图如图7(a)所示，即放开上下、前后、俯仰3个自由度。计算坐标原点位于无人平台首部，位移及速度计算参考点位于无人平台重心处，如图7(b)所示。

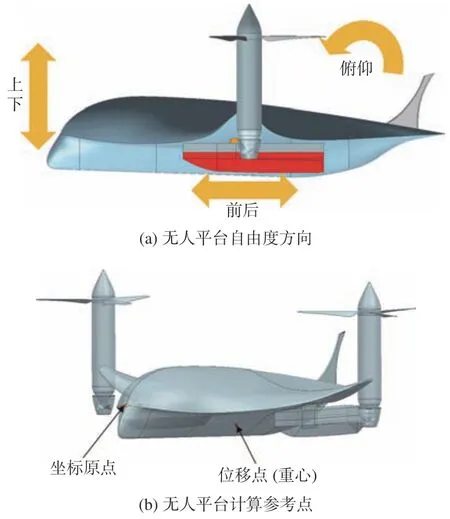
图7 自由度方向及参考点示意图Fig.7 The schematic diagram of direction of freedom degree and reference points

分析无人平台开始从水面起飞的0.9 s内上升位移随时间的变化情况，如图8所示。从中可以看到，在螺旋桨转速N=2 352 r/min时无人平台开始是向上移动的，但约0.5 s后开始下降，说明在2 352 r/min转速下空气螺旋桨无法提供顺利拉起无人平台（一半为30 kg）所需的拉力。

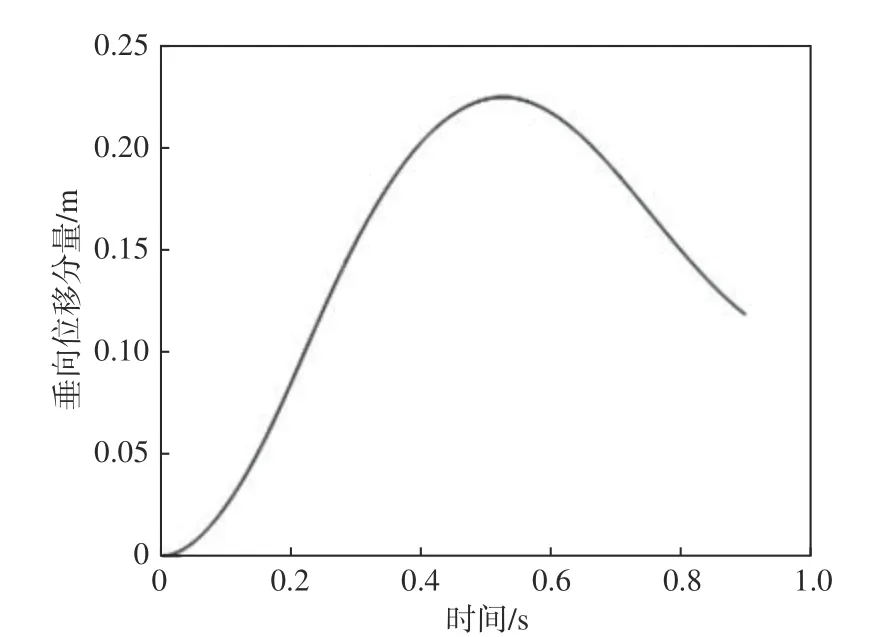
图8 N=2 352 r/min时的垂向位移分量Fig.8 The vertical displacement components at N=2 352 r/min

考察无人平台开始从水面起飞的0.9 s内单桨拉力，如图9所示。从中可以看到，在螺旋桨转速N=2 352 r/min下空气螺旋桨的拉力T基本稳定在219 N，确实无法顺利拉起重量为30 kg的无人平台（此处取一半计算）。

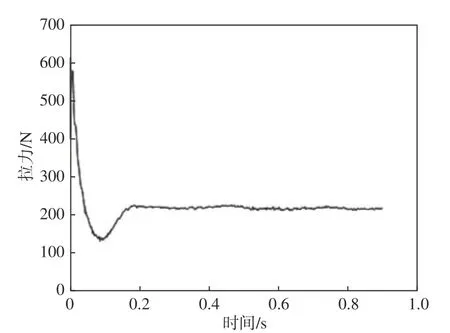
图9 N=2 352 r/min时的单个螺旋桨拉力Fig.9 The single air propeller pull force at N=2 352 r/min

为了能够顺利从水面起飞，根据空气螺旋桨提供的实际升力并结合表2中数据进行换算，预估空气螺旋桨转速至少达2 840 r/min时才能拉起无人平台。因此，选取2 840 r/min作为空气螺旋桨转速，重新针对无人平台起飞过程中的运动特性与动态特性进行计算，其中自由度示意图仍如图6所示，即放开上下、前后、俯仰3个自由度。

2.3.1 起飞特性

选择无人平台开始从水面起飞1.6 s的数据对起飞特性进行比较分析。分析起飞运动特性时，主要针对无人平台上升的位移随时间的变化，以及向上的速度分量随时间的变化进行比较。

图10所示为无人平台开始从水面起飞运动时向上的位移分量。从中可以看到，当螺旋桨转速N=2 840 r/min时无人平台向上移动的速度更快，且被顺利拉起升离水面。

图10 N=2 840 r/min时的垂向位移分量Fig.10 The vertical displacement components at N=2 840 r/min

图11所示为无人平台开始从水面起飞运动时向上的位移速度。从中可以看到，当螺旋桨转速N=2 840 r/min时无人平台主要存在2个较明显的加速区和1个减速区，其中0～0.2 s为第1个加速区，0.2～0.72 s为减速区，0.72 s之后为第2个加速区。

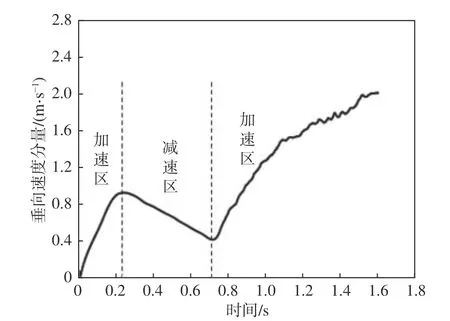
图11 N=2 840 r/min时的垂向速度分量Fig.11 The vertical velocity components at N=2 840 r/min

分析起飞过程中空气螺旋桨拉力与无人平台在垂直方向的整体受力情况分别如图12和图13所示。其中，无人平台的整体受力包含螺旋桨拉力、无人平台重力和起飞过程气动力。

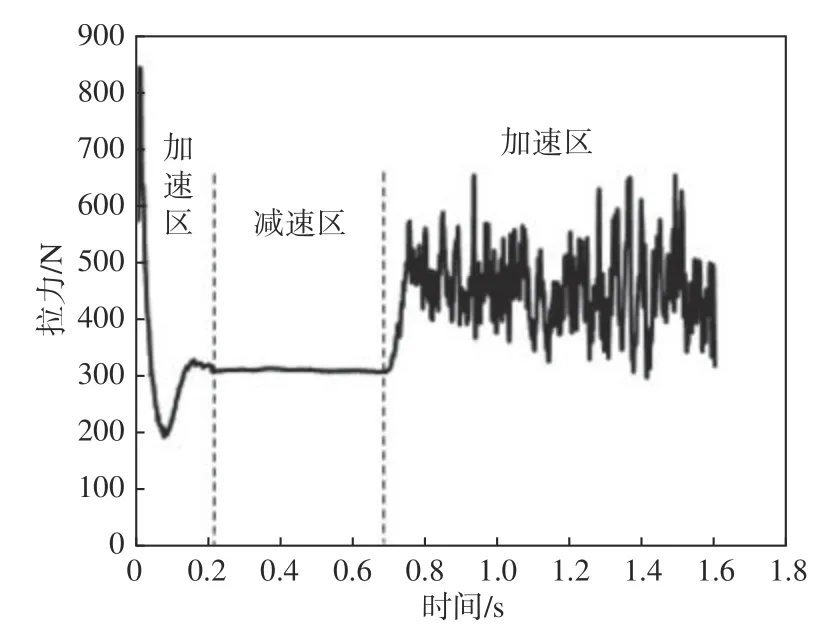
图12 N=2 840 r/min时的空气螺旋桨拉力Fig.12 The air propeller pull force at N=2 840 r/min

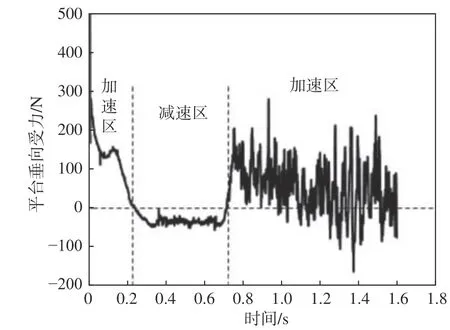
图13 N=2 840 r/min时的无人平台垂向受力Fig.13 The vertical components of force on unmanned vehicle at N=2 840 r/min

由图12和图13可以看到，在第1个上升加速区，随着无人平台逐渐上升，浮力减小，整体垂向受力逐渐减小至0。在上升减速区，空气螺旋桨拉力保持稳定，无人平台整体垂向受力为负值，究其原因，是因为随着上升速度的增加，无人平台的上升阻力（气动力）也随之增加。在第2个上升加速区，受无人平台与空气螺旋桨气动力耦合作用的影响，螺旋桨拉力开始波动，对比上升减速区瞬间（t=0.4 s）和第2个上升加速区瞬间（t=0.85 s），空气螺旋桨的表面压力系数分布如图14和图15所示。其中，压力系数CP的定义为：

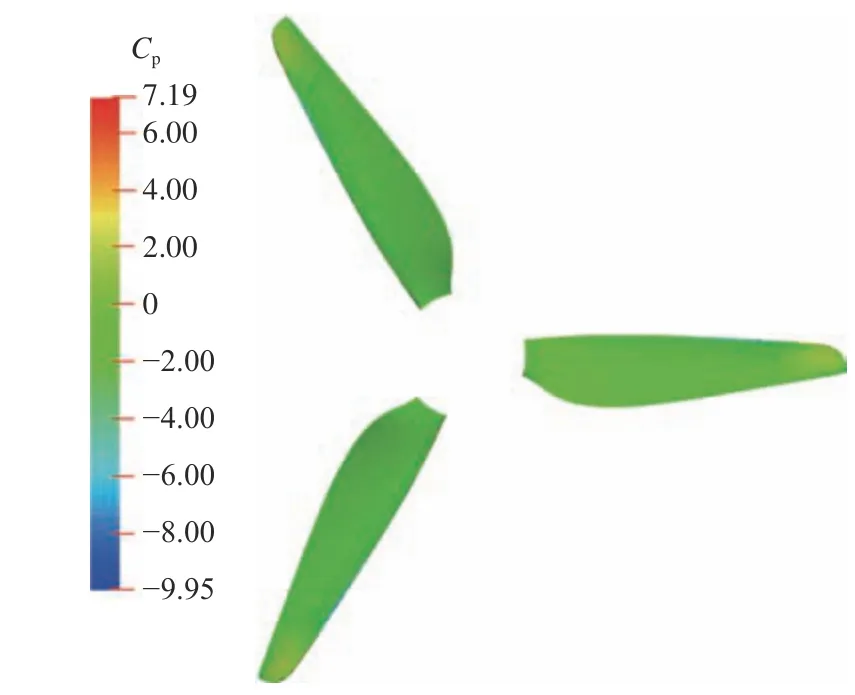
图14 t=0.4 s时螺旋桨表面压力系数分布Fig.14 The pressure coefficient distribution on air propeller surface at t=0.4 s

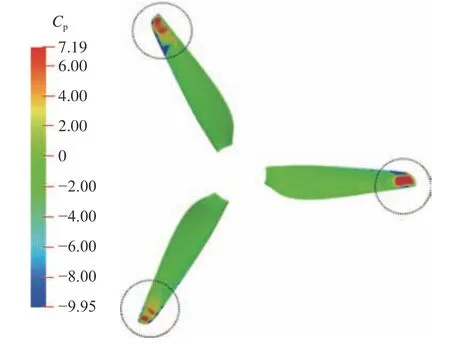
图15 t=0.85 s时螺旋桨表面压力系数分布Fig.15 The pressure coefficient distribution on air propeller surface at t=0.85 s

式中：P为当地压力；P∞为远前方压力。

对比图14和图15可以看到，与上升减速区相比，在第2个上升加速区空气螺旋桨的表面压力存在明显的非稳定低压与高压集中区，这也是空气螺旋桨拉力剧烈波动的原因。

此外，对比上升减速区瞬间（t=0.4 s）和第2个上升加速区瞬间（t=0.85 s），得到无人平台主体上表面的压力系数分布分别如图16和图17所示。同样，从图中可以看到，与上升减速区相比，在第2个上升加速区无人平台主体的上表面压力明显增加且更加不均匀，这也将导致无人平台整体垂向受力波动明显。

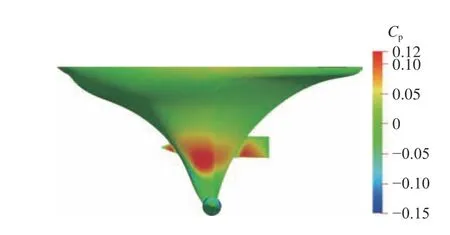
图16 t=0.4 s时无人平台上表面压力系数分布Fig.16 The pressure coefficient distribution on the upper surface of unmanned vehicle at t=0.4 s

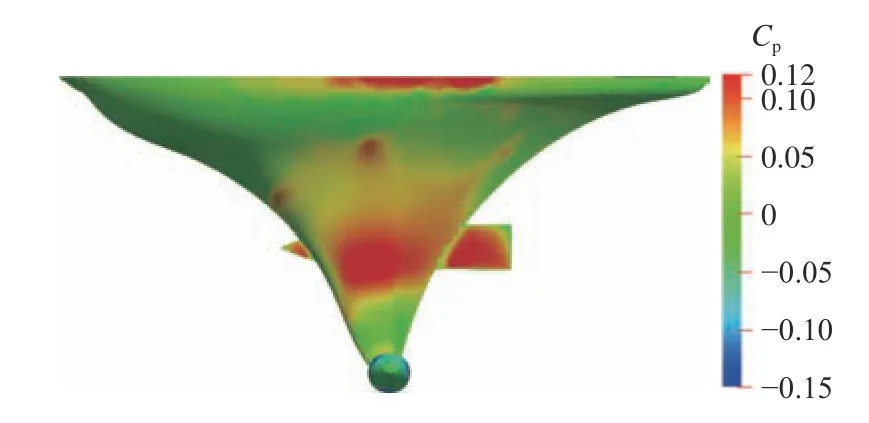
图17 t=0.85 s时无人平台上表面压力系数分布Fig.17 The pressure coefficient distribution on the upper surface of unmanned vehicle at t=0.85 s

为分析无人平台起飞过程中自由液面的形态以及周围流场的变化，选取上升减速区瞬间（t=0.4 s）和第2个上升加速区瞬间（t=0.85 s）的自由液面波高分布及无人平台下表面压力系数分布情况，分别如图18～图21所示。从中可以看到，无人平台从水面起飞出水过程中，自由液面的波高Hw分布不均匀性较明显，但当无人平台完全升离水面后，自由液面的波高Hw分布不均匀性明显降低。分析图19和图21可知，自由液面变化对无人平台下表面的压力系数分布影响较小，这主要是因为无人平台采用的是小水线面船体结构，下表面与水的接触面较小。

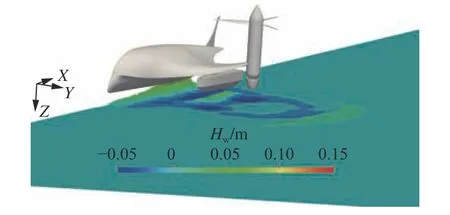
图18 t=0.4 s时自由液面波高分布Fig.18 The wave height distribution on free surface at t =0.4 s

图19 t=0.4 s时无人平台下表面压力系数分布Fig.19 The pressure coefficient distribution on the lower surface of unmanned vehicle at t =0.4 s

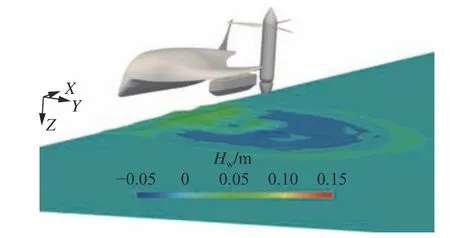
图20 t=0.85 s时自由液面波高分布Fig.20 The wave height distribution on free surface at t =0.85 s

图21 t=0.85 s时无人平台下表面压力系数分布Fig.21 The pressure coefficient distribution on the lower surface of unmanned vehicle at t =0.85 s

2.3.2 平移特性

无人平台从水面起飞时的水平位移分量如图22所示。从图中可以看到，当螺旋桨转速N=2 840 r/min时，无人平台一直保持向前运动。

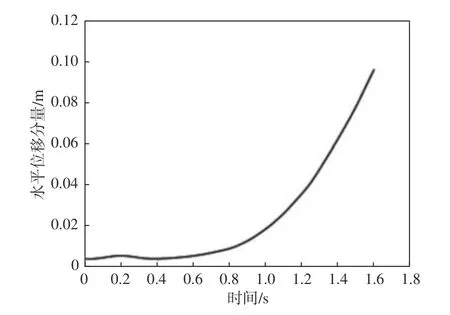
图22 N=2 840 r/min时的水平位移分量Fig.22 The horizontal displacement components at N=2 840 r/min

无人平台从水面起飞时的水平速度分量如图23所示。从图中可以看到，当螺旋桨转速N=2 840 r/min时，无人平台主要存在2个较明显的加速区，其中0.2～0.72 s为第1个加速区，0.72 s之后为第2个加速区，且第2个加速区的加速度更大。但与图11所示的垂向速度相比，无人平台的水平速度值偏小，达到一个数量级，即无人平台的主运动为垂向上升运动。

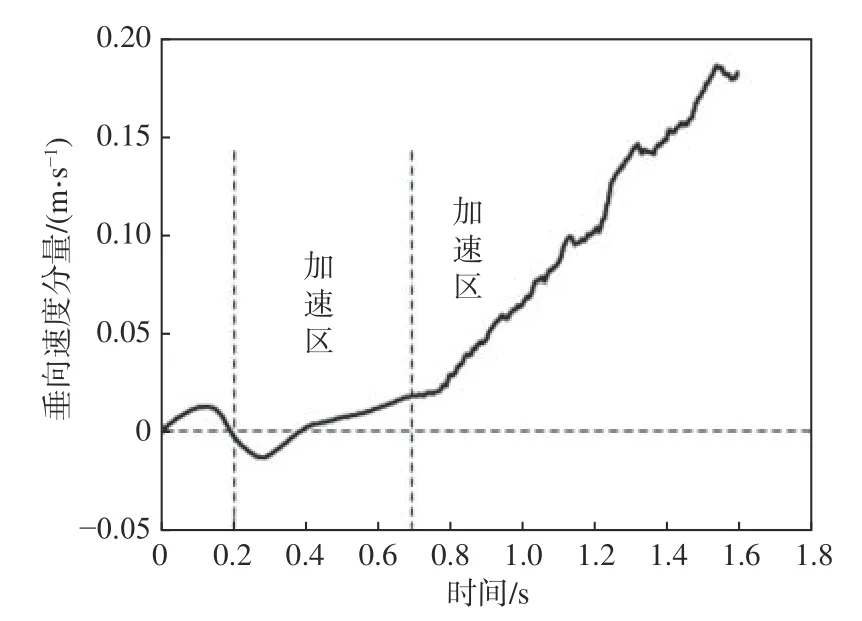
图23 N=2 840 r/min时的水平速度分量Fig.23 The horizontal velocity components at N=2 840 r/min

分析无人平台在水平方向的受力如图24所示。从中可以看到，对应第2个平移加速区的无人平台水平受力均值大于第1个平移加速区。

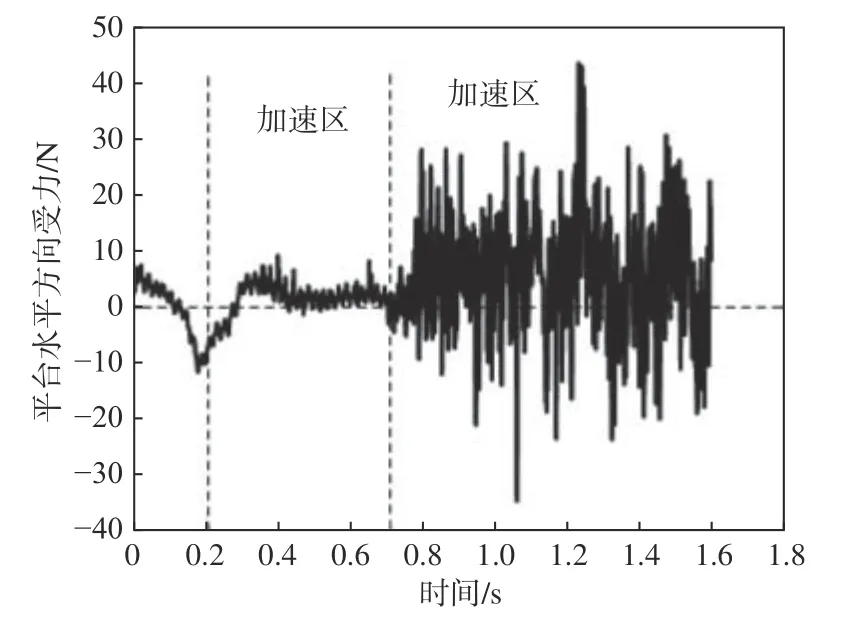
图24 N=2 840 r/min时平台的水平受力Fig.24 The horizontal components of force on unmanned vehicle at N=2 840 r/min

2.3.3 俯仰及载荷特性

图25所示为跨域无人平台在起飞过程中俯仰角的变化曲线，该角度定义为原理样机绕横轴的旋转角度，机头抬高、机尾下降为正，反之为负。由图中可以看到，在螺旋桨转速N=2 840 r/min下，无人平台在0.72 s之前俯仰角变化较小，在0.72 s之后俯仰角变化较大，存在快速低机头现象。分析图26所示的无人平台俯仰力矩可知，在0.72 s之前俯仰力矩变化较小，在0.72 s之后俯仰力矩变化较大，且波动明显。这表明原理样机极有可能失稳，因为此时未加入控制程序，所以在该状态下无人平台最终会失稳，从而无法顺利垂直起飞。

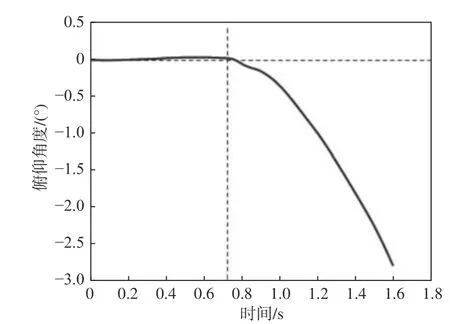
图25 N=2 840 r/min时无人平台的俯仰角度Fig.25 The pitch angle of unmanned vehicle at N=2 840 r/min

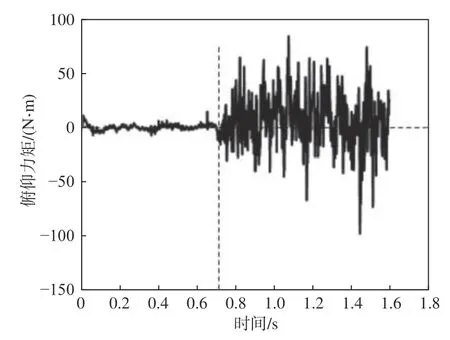
图26 N=2 840 r/min时无人平台的俯仰力矩Fig.26 The pitch moment of unmanned vehicle at N=2 840 r/min

图27所示为螺旋桨转速N=2 840 r/min时无人平台快速低头瞬间（t=1.6 s）的原理样机表面的压力分布。从中可以看到，空气螺旋桨高速的下洗气流冲击在无人平台上表面，使得以横轴为界，至机头的总体压力大于至机尾的总体压力，出现了将机头向下压的状态。随着无人平台“低头”，在总体下压载荷作用下无人平台的俯仰角变化呈指数形式上升，最终导致无人平台失稳及坠落。因此，为保证无人平台顺利升空，在水面至空中的垂直起飞阶段必须加入手动或自动的控制程序，以实时调整推进器倾转角度。

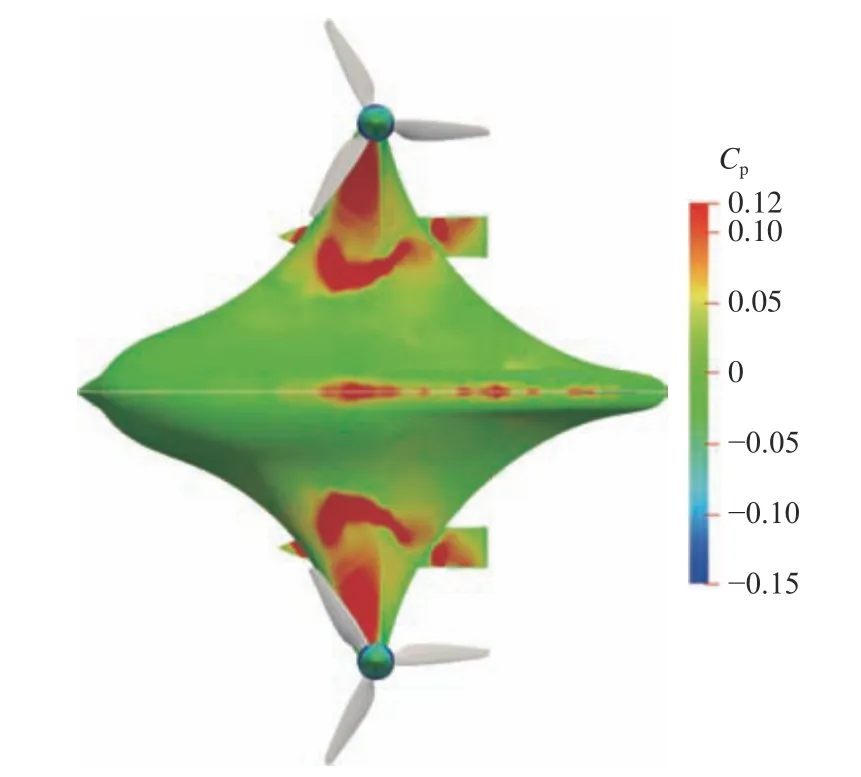
图27 N=2 840 r/min，t=1.6 s时无人平台表面压力分布Fig.27 The pressure distribution on the surface of unmanned vehicle at N=2 840 r/min and t=1.6 s

3 结 论

本文针对跨域无人平台浮于水面平稳后进行的垂直起飞动态过程，采用数值模拟方法进行了仿真研究，主要得到如下结论：

1） 在垂直起飞过程中，无人平台会受到上升阻力的影响，需要空气螺旋桨以相对于单桨等拉力状态更高的转速将无人平台拉起升离水面，其主运动为垂向上升运动。

2） 由于空气螺旋桨的下洗气流在无人平台机身表面形成了机头压力大、机尾压力小的现象，在起飞过程中会出现“快速低头”的现象，最终导致无人平台失稳及坠落，因此，为保证无人平台顺利升空，在水面至空中的垂直起飞阶段必须加入手动或自动的控制程序，用以实时调整推进器倾转角度。