基于“5E”教学模式,培养核心素养
2022-03-19方文婷田芳
方文婷 田芳


[摘 要] 教学设计是落实核心素养的关键环节,其有效落实需要合适的教学模式. 由美国生物学课程研发中心提出的“5E”教学模式遵循了学生的认知规律,强调“以学生为主”及让学生进行科学探究,是一种有效的探究式教学模式[1]. 文章将“5E”教学模式应用于“点的位置与坐标”第一课时,通过“活动+问题串”引导学生全程参与课堂教学. 课后对学生进行了问卷调查,分析相关数据可知:“5E”教学模式对学生数学核心素养的培养确有帮助.
[关键词] “5E”教学模式;点的位置与坐标;活动课;教学设计;核心素养
问题的提出
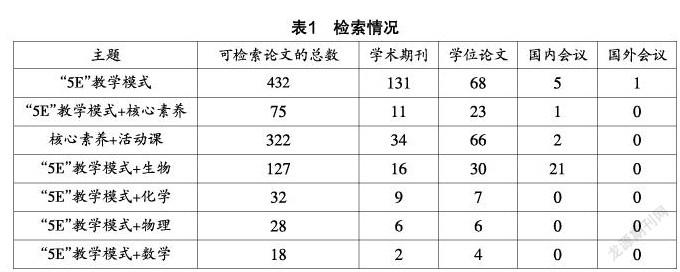
1989年,美国生物学课程研究中心(BSCS)研发出了符合当代实际教学的教学模式——“5E”教学模式,其包含5个主要环节,分别是吸引(Engagement)、探究(Exploration)、解释(Explanation)、迁移(Elaboration)和评价(Evaluation),因各个环节的名称均以字母“E”开头,故简称“5E”教学模式. “5E”教学模式历经30多年的研究与发展,实践表明其在一定程度上能够促进学生的学习兴趣和学习结果,同时为培养学生核心素养提供了实可参考的实践素材[2]. 为进一步了解“5E”教学模式在国内的研究现状,在中国知网围绕相关研究内容进行了检索,检索情况如表1所示.
由数据可知,“5E”教学模式与核心素养的关系存在着相当大的研究价值,核心素养与活动课的关系可以近似地看作是目标与途径的关系. 所以,对于中学数学学科,三者(“5E”教学模式、核心素养、活动课)之间的关系必然存在着研究价值.
在高级检索中以主题“‘5E’教学模式+数学”进行检索,共有18篇文献可供参考,时间跨度为2014年至2021年. 可见,“5E”教学模式在数学领域中的研究较晚且成果不多,相关研究成果主要分为以下三类:
(1)理论层面.李欢从“5E”教学模式的内涵出发,得出该模式是一种旨在引起学生学习兴趣的教学模式,在了解学生的前科学概念和培养学生的数学探究能力等方面极其有效[3].
(2)教学实践方面.黄一娉将“5E”教学模式运用于高中数学复习课的实验教学环节并得出:“5E”教学模式可以使实验班学生的数学学习成绩显著改善,对学生的数学理解、问题解决、情感态度、学习方式、思维水平等方面都产生了积极的影响[4];陈算荣、陈建祥和郑兆圣应用“5E”教学模式对“锐角三角函数”进行了教学设计和教学实践研究,实践结果表明该模式的5个环节与教师教学过程的5个层次相对应[5];洪玉以“函数”和“对数”为例,应用“5E”教学模式对高中数学概念课进行了教学实践研究,对“5E”教学模式的各个环节给出了教学指导,给出了该模式应用于课堂教学的两个基本条件[6];程琳应用“5E”教学模式引导小学生探究学习,指出在小学数学教学中有效地应用“5E”教学模式可以激发学生的学习兴趣,帮助学生掌握数学知识,提高教学质量[7].
(3)课例展示方面.黄一娉、黄梦远和唐剑岚基于“5E”教学模式对数学实验课进行了教学设计[8];侯煜群以“直线与平面平行的判定”为例展示了“5E”教学模式在数学中的应用[9];龙非凡和周莹以“勾股定理”为例进行了教学设计,给出了“5E”教学模式在数学教学中的应用策略[10].
综上,国内关于“5E”教学模式在数学领域的研究范圍从小学到高中,课型有复习课、概念课、实验课、定理课等,目前尚未出现活动课. 所以,文章选择将“5E”教学模式放入中学数学活动课. 原因如下:
(1)活动课提供了丰富的活动经历和思维材料,是发展数学核心素养的有效载体.
(2)活动课可以引导学生进行数学活动,重视学生提出问题和解决问题的整体过程,提倡深度学习、积极反思[11],这与“5E”教学模式的教学环节相契合.
所以,将“5E”教学模式、活动课、核心素养联系在一起,探讨三者之间的关系,对学生数学核心素养的培养有一定的研究意义.
总体教学分析及设计
“点的位置与坐标”作为第一课时,选自北师大版八年级上册的数学教材;主要内容为平面直角坐标系的建立,使点与数的对应关系实现由一维到二维的过渡,这将为用代数方法研究几何问题提供重要的数学工具.
学生在小学已经学过“用数对表示位置”,所以本节课对学生来说并不陌生;但对于中学生,由此出发抽象出平面直角坐标系的思维活动并不简单,故将其设计为一节活动课是合适的. 这可以起到概念阐述直观生动、表象鲜明,思维表达具体可见、清新自然的作用,让学生形成良好的数学直觉极为重要;同时可以调动学生的手、脑、眼,利于培养学生的综合思考能力.
具体的教学目标如下:
(1)理解平面内点的坐标、平面直角坐标系等概念;根据平面直角坐标系写出点的坐标,根据点的坐标确定点的位置,明确点的坐标与点的位置一一对应的关系;能结合具体情境,灵活运用多种方式确定点的位置;理解平面直角坐标系内特殊点的坐标特征.
(2)经历平面直角坐标系建立的过程,在具体的活动中感受特殊点的坐标特征,进一步发展数形结合思想.
(3)通过亲身参与四个活动,感受数学来源于生活又服务于生活.
课前准备:
(1)教室准备:将单人桌合并排列,使其前后左右间隔距离相等.
(2)教具准备:投影仪一台,磁性黑板一块,PPT7张,两根装有箭头的长绳且标有字母x,y,表示数轴上点的坐标的数字卡片若干(0,±1,±2,±3,±4,…).
活动形式:
把教室地面作为平面直角坐标系,每位学生的座位作为平面内的一个点,组织4次活动,研究平面内点的位置与坐标.
具体教学过程及解读
1. 吸引(Engagement)
“5E”教学模式的吸引环节要求教师创设与学生现实生活贴近的问题情境,引起学生的认知冲突,使学生暴露出现有的知识水平.
创设情境1:母亲节那天,小丽同学的母亲的单位准备发放电影票,有两部电影可供选择:一部是母亲期望已久的生活片《八月》,一部是小丽心心念念的《哈利波特》,但每人只能领取一张电影票,你们猜测小丽同学的母亲领了哪一张电影票?为什么?
教学处理:小组讨论后,请学生举手选择;大多数学生认为小丽同学的母亲领取的是《哈利波特》,原因是大多数学生“以己母之所好,推及人母之所好”.
师:大多数同学回答得正确,母亲为小丽领取了一张电影票. 请同学们想想:小丽到达电影院后会怎么找到自己的座位呢?
教学处理:这是本节课要处理的关键问题,给学生充分的思考时间和表达时间,不急于判断对错.
设计意图 短短3分钟,在不影响课程进度的情况下,能使学生感受到母爱亲情的教育,同时明确平面内确定点的位置需要两组数据,激发学生解决问题的欲望,帮助学生进入新概念的学习.
2. 探究(Exploration)
“5E”教学模式的探究环节要求教师根据学生现有的概念认知、过程认知及技能,创设一个共同的任务,让学生通过操作或实验,运用原有知识形成新概念、产生新方法,探索新问题和可能产生的结果.
探究活动1:
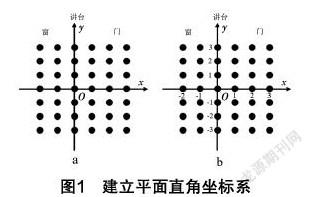
师:请同学们以竖排为列,横排为行,有序地排成六列七行,具体规则如图1(a)所示;接着用两根标有x,y的长绳,以第四行、第三列所在直线分别为x轴、y轴,将教室建立成一个平面直角坐标系,如图1(b)所示.
师:比较第二行第三列位置上的学生与第三行第二列位置上的学生,他们是同一人吗?在平面直角坐标系内,怎样表示两位同学所在位置的坐标呢?
教学处理:让学生带着问题进行探索,发现两个位置上的不是同一人;便于区分,教师引导学生分别用有序数对(3,2)与(2,3)表示,同时讲解点的坐标的概念.
探究活动2:
师:在建立的平面直角坐标系内,设每位同学表示一个点,每两位同学之间间隔一个单位长度.
师:接下来请每位同学依次报出自己位置的坐标.
活动完成后,教师随机说出一个坐标,学生要迅速说出该位置(坐标)上的人是谁.
设计意图 将课本上广播操的队形换成教室中的座位,使学生身临其境,获得一定的感性认识;从第二行第三列位置上的学生与第三行第二列位置上的学生的区别,突出在平面上用有序数对表示位置的合理性. 设置活动:请学生报出自己位置的坐标,以及教师给出坐标让学生寻找对应的同学,进而达到本节课的教学目标.
3. 解释(Explanation)
“5E”教学模式的解释环节要求学生解释自己对概念的理解,教师的解释引导学生步入深层次理解.
师:(在图2的投影下)请同学们为坐标轴、坐标原点、平面直角坐标系、点的坐标下定义.
教学处理:组织学生先小组讨论,请小组代表发表看法,小组的其他学生进行补充及修正;针对学生回答的情况,教师加以补充,使学生形成正确的概念;初次介绍象限的概念,用PPT展示概念.
设计意图 解释环节给了学生思考、反思本质的机会,学生需要进一步理解概念.
探究活動3:
师:(了解了象限的概念之后)请在第一象限的同学站起来,每人说出表示自己位置的坐标,再回答你们所在象限的坐标有什么特征. (第二象限以此类推)
师:想一想,第三象限内点的坐标有什么特征?请在第三象限的同学站起来,检验前面的结论是否正确.
全班共同探讨第四象限内点的坐标的特征,并让学生站起来加以验证.
师:请位置在x轴上的同学站起来,观察其坐标有何特征;请位置在y轴上的同学站起来,观察其坐标有何特征.
教学处理:请学生大胆说出自己的想法,其他学生和教师一起补充和修正,最后用PPT呈现总结.
设计意图 采用小组讨论和亲身实践,确保所有的学生都能参与其中,使学生在轻松的学习氛围中了解四个象限内点的坐标的特征,突破并掌握坐标轴上点的坐标的特征这个教学难点;最后教师给出标准答案,让学生明确自己的回答不足.
探究活动4:
师:在我们中有满足这样坐标的同学吗?坐标为(1,1),(2,2),(3,3),(-2,-2),(0,0),请你们站起来并想一想你们所站的位置在哪个象限内.
师:第二、第四象限的角平分线上的点的坐标有什么特征呢?
师:请横坐标是“2”的同学站起来,观察其位置有何特征;请纵坐标是“-2”的同学站起来,观察其位置有何特征.
想一想,试一试:将两根表示数轴的绳子的交点换一个位置,你的位置变化了吗?你所在位置对应的坐标变化了吗?
教学处理:学生给出答案后,教师加以鼓励,同时指明今后为了研究数学问题,可以选择适当的位置建立平面直角坐标系.
设计意图 解释环节聚焦了前两个环节(吸引环节和探究环节)的某个具体方面,为学生提供了机会去说明自己的概念性认识、方法技能或行为,强调学生是学习的主体,教师只是教学的引导者. 利用探究活动3和探究活动4,使学生在亲身参与的过程中为各个概念下定义,掌握平面直角坐标系的特征.
4. 迁移(Elaboration)
1976年7月28日凌晨,我国河北省唐山市发生了里氏7.8级的大地震,这次地震造成242769人死亡,164851人重伤,位列20世纪世界地震史死亡人数第二. 地震中心位于东经118.2°,北纬39.6°. 你能在地图上找出地震中心的大致位置吗?
教学处理:学生独立操作完成,教师有序组织汇报.
设计意图 迁移是“5E”教学模式的拓展提升环节,具有迁移之意. 通过设计不同情境的问题来挑战学生,完善学生的知识框架,使认知更加全面,进而让学生感悟数学来源于生活又服务于生活.
5. 评价(Evaluation)
师:平面内,如何确定一个点的位置?平面直角坐标系内点的坐标各有什么特点?你还能找出哪些规律?
师:在本节课的学习中,你经历了哪些学习过程?谈谈你的收获.
教学处理:由学生分小组进行讨论,选小组代表进行总结性回答.
设计意图 提出这样的开放性问题不仅可以让教师了解学生的学习情况,同时教师还可以根据学生的回答对本节课的主要内容做一个总结,给予学生充分的机会去审视自身在这节课中具体有哪些收获与不足.
反馈与感悟
1. 学生的反馈
选取宁夏固原市两所初级中学四个班的数学教师在同一天授课,课例实施以后,针对四个班的学生在本节课的学习体验进行了简单的问卷调查,共发放问卷265份,回收264份,回收率99%;其中男生124人(47%),女生140人(53%). 应用SPSS 24.0进行数据分析,可知該调查问卷的克隆巴赫(信度)系数α=0.841,具有良好的信度.
由图3可得,75%的学生喜欢基于“5E”教学模式的数学活动课,对本节课持喜爱态度;81%的学生认为顺利地学习了本节课的内容;69%的学生希望老师能多上这种数学活动课;71%的学生认为通过本节课的学习,自己的学习能力有所提升. 究其原因,在于“5E”教学模式的教育理念是以学生为主体,主张把课堂还给学生,结合活动课的相关授课要求,使学生真正地在做中思、在做中学、在做中说、在做中结,一切活动都由学生自己完成,所以受到学生的一致好评.
为了进一步调查学生的学习能力
在哪些方面得到了提升,笔者在问卷调查中设计了如下问题:通过本节课的学习,你认为自己的学习能力在哪些方面得到了提升(多选)?调查结果如图4所示.
由图4可知,71%的学生认为自己的空间观念有所提升;65%的学生认为自己的应用意识有所提升;62.5%的学生认为自己的数据分析观念有所提升;其他选项均有学生选择,但人数并不集中,在此不再分析. 由图4可知,作为多选问题,每位学生的具体选项数没有限制,所以共有767个选项数. 观察调查问卷,大多数学生选择了4个选项,若以此为基准,则有73%的学生认为自己的核心素养有所提升.
2. 关于“5E”教学模式应用于中学数学活动课的思考
(1)“5E”教学模式适用于中学数学活动课教学.
“5E”教学模式的指导理论为建构主义理论和概念转变理论,其应用和研究多集中于概念教学,这确实为中学数学概念课的教学提供了一种新思路,但研究成果并不多. 笔者认为,其原因是概念教学的指导理论在我国中学数学教学中已经相当成熟. 查阅文献发现,“5E”教学模式在生物学科、化学学科被广泛应用,已经成为一种常用的教学模式,溯其根源在于各环节的相关要求与生物学科、化学学科的课堂要求相契合. 为了进一步将“5E”教学模式运用于数学课堂,扩大其应用范围,笔者选择了一种特殊的课型——活动课. 原因如下:
课堂展开:一方面,活动课改变了学生单一的学习活动方式, 在活动的过程中,学生不仅能获得数学知识,更能积累基本活动经验;另一方面,“5E”教学模式的特色在于提倡学生以合作交流的学习方式为主,通过参与、探究、解释、精致和评价等学习环节完善学生的数学基本活动经验[12];相较于传统的教学方式,学生通过“5E”教学模式习得的知识牢固性更高,二者在学生积累数学活动经验方面都发挥了重要的作用.
核心素养:一方面,活动课是数学课堂的重要组成部分,它是对数学知识的综合应用、是学生开展综合实践活动的重要平台、是学生数学核心素养的集中体现[13]. 另一方面,“5E”教学模式正是美国为发展科学素养提出的一种教学模式,也是为发展核心素养提出的一种教学方法,二者实施的终点与目的均与核心素养相关,故将“5E”教学模式应用于中学数学活动课是合适的.
(2)“5E”教学模式应用于数学课堂的必要性.
新一轮课程改革将“双基”改成了“四基”,增加了基本思想和基本活动经验,但数学教学是否真正落实了“四基”,学生在教学中是否真正达成了数学“四基”目标,目前文献尚少提及[14]. “5E”教学模式强调以学生为主,调动学生的积极性,通过调查、实验的方式来解决问题,注重经验的积累,所以“5E”教学模式在落实“四基”方面可以发挥相当大的作用,走进数学课堂已成为大势所趋.
此外,史宁中教授理想的教学过程与“5E”教学模式各环节的要求不谋而合,因而在教学理论方面也说明“5E”教学模式应被数学课堂广泛采用,二者具体的对应关系见图5[15].
(3)“5E”教学模式的应用需要灵活处理.
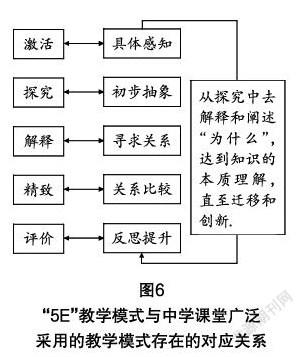
通过文献查阅和上述课例的实践,笔者认识到,在应用“5E”教学模式进行活动课教学时,各环节发挥着不同的作用,课堂运用的效果如何,取决于教师对学生学情的掌握和重难点的把握,教师一定要体会“5E”教学模式的精髓,在课堂灵活处理. 具体而言,教师要明确:吸引环节和探究环节是构建新知识的数学实践过程,其中探究环节是基于吸引环节的活动结果的指向,把学生置于探索和发现的环境中,达成揭示和体验新知识、新方法、新经验等形成过程的目的. 解释、迁移和评价三个环节是知识逐步内化的关键[16]. 这与当前中学课堂广泛采用的教学模式存在着对应关系,见图6.
故在实际的教学过程中,教师需要注意:“5E”教学模式不是一种全新的教学模式,教师在使用该模式进行教学时,不能停留在表面的模仿层面,而应充分理解理论的基础和精髓,灵活变通,不断反思与实践,最终落实课程理念和课程目标[17].
(4)“5E”教学模式需要广大数学研究者继续探究.
“5E”教学模式是科学教育领域的现代教育模式,在我国的理科教育中,恰当运用该教学模式进行教学,将有助于落实课程理念和课程目标,更有利于提升学生的学业成就、学习兴趣[18]. 但“5E”教学模式在我国的研究领域多集中在生物、物理、化学等学科;随着研究领域的深入和拓展,数学、英语、地理等学科都有所涉及,但研究成果主要集中在理论层面,实践层面尚不多见. 本文章在目前研究成果的基础上,将“5E”教学模式的应用范围从概念课扩大至活动课,为中学数学活动课的教学设计提供了思路,为“5E”教学模式走进数学课堂提供了路径;但本文章采用的是“定性研究+定量研究”,结合相关问卷的数据进行分析,存在一定的局限性.
改革开放以来,我国引进了大量的外国教育理论,并对这些理论进行了充分的学习和讨论,但是对这些理论运用的研究,总体上还比较薄弱.如果不能把理论贯彻于实践,那只能是空头理论[19]. 综上所述,探究“5E”教学模式在中学数学教学中的应用是有现实性和必要性的,而且也具有一定的创新性和实用价值. 将“5E”教学模式应用于中学数学教学,不仅能为中学数学教学实践提供理论指导和方法指导,也能为教学改革提供一定的借鉴思路. 这些工作需要广大的研究者在前人研究的基础上继续探究.
参考文献:
[1]Bybee, R.W.The BSCS 5E instructional model and 21st century skills [J]. Colorado Springs,Co: BSCS,2009(29).
[2]李林. 基于“5E”教学模式的高中生物学教学的实践研究[D]. 四川师范大学,2019.
[3]李欢. 5E教学模式对我国中学数学教学的启示[J]. 理科考试研究,2014,21(15):2.
[4]黄一娉. 基于5e学习环的高中数学复习课实验教学模式研究[D]. 广西师范大学,2017.
[5]陈算荣,陈建祥,郑兆圣. “5E”模式下的锐角三角函数概念教学[J]. 教育研究与评论(中学教育教学版),2018(07):86-90.
[6]洪玉. 基于“5E”教学模式的高中数学概念课的教学实践研究[D]. 辽宁师范大学,2020.
[7]程琳. 应用5E教學模式引导学生探究数学[J]. 小学时代,2020(15):23-24.
[8]黄一娉,黄梦远,唐剑岚. 基于5E学习环和HP工具的数学实验创课设计——以“函数图象平移变换”的教学为例[J]. 中小学课堂教学研究,2017(06):14-18.
[9]侯煜群. 5E教学模式在数学教学中的应用——以一节高中数学课为例[J]. 数学学习与研究,2018(17):85-86.
[10]龙非凡,周莹. 基于5E教学模式的初中数学定理教学设计——以“勾股定理”为例[J]. 中小学课堂教学研究,2018(09):26-29+40.
[11]顾广林. 指向数学核心素养的初中“数学活动”教学[J]. 江苏教育,2020(51):36-39.
[12]张玉红. 小学生数学基本活动经验的积累[J]. 教学与管理,2020(23):40-41.
[13]陈春涛. 应用图形计算器培养学生数学核心素养例析——以数学活动课的教学为例[J]. 教育信息技术,2019(Z2):59-61+56.
[14]曾峥,杨豫晖,武金艳. 数学“四基”的研究现状及展望[J]. 数学教育学报,2017,26(02):66-70.
[15]陈算荣. 数学核心素养落地课堂——五“E”教学模式解析[J]. 中学数学教学参考,2017(33):62-64.
[16]陈算荣,陈建祥,郑兆圣. “5E”模式下的锐角三角函数概念教学[J]. 教育研究与评论(中学教育教学),2018(07):86—90.
[17]张博,周莹. 立足5E教学模式 发展数学核心素养——以“双曲线及其标准方程”的教学为例[J]. 高中数学教与学,2019(18):30-32.
[18]李娜,刘艳超,杨薇. 基于5E模式的中学物理教学研究—以《物体的沉浮条件及应用》为例[J]. 物理教学探讨,2014,32(05):5-8.
[19]涂荣豹. “教与数学对应”原理的实践——对“函数单调性”教学设计的思考[J]. 数学教育学报,2004(04):5-9.
3165501908206
