考虑粗糙度的新型三叉式万向联轴器润滑分析∗
2022-03-18魏建宝李松梅
许 婷 魏建宝 李松梅
(青岛科技大学机电工程学院 青岛 266061)
1 引言
无论是单个联轴器还是整个联轴器系统,由于结构和其他附加因素的存在,它们都会产生各种类型的振动。这些振动效应使得单个联轴器和整个联轴器系统摩擦磨损加剧,最终会导致联轴器寿命降低。新型三叉式万向联轴器主要将直线轴承结构应用到三叉槽内,在三叉槽内加上滚珠,使滑块与三叉槽面接触改为滑块与滚珠的点接触,从而降低摩擦,其三维模型如图1 所示。为了有效地降低振动和磨损带来的不良后果,添加润滑油是降低摩擦阻力磨损的一项重要技术措施[1~2],但是润滑油对其润滑效果,还要深层次探究。
国外学者Guegan等[3]研究了沿滚动-滑动方向的粗糙度脊线对滚动轴承弹性流体力学润滑的影响,发现引入粗糙度时会影响速度和最小膜厚;
Hiremath 等[4]采用多重网格法求解具有表面粗糙度的等温、可压缩弹流润滑线接触问题,发现综合压力越大,最小膜厚增厚;Andre 等[5]提出了一种预测弹流润滑稳态和瞬态条件下膜厚变化的线和点接触的解析模型,发现膜厚、碾压力、润滑剂三者有一定联系;Zolper 和Cyriac 等[6~7]对六种酯基油的润滑性能进行研究,得到油膜厚度随温度的升高而减小,速度也是决定油膜厚度的因素之一;Morteza等[8]采用混合润滑模型,通过激光表面花纹对ST37 圆盘线接触磨合和稳态进行实验和分析,结果表明增加速度和减少施加的载荷会导致磨损率的降低。国内学者周江敏和路遵友等[9~10]研究线接触润滑,考虑了表面粗糙度和热效应对润滑特性的影响;陈佳等[11]研究了在等温非牛顿流体条件下,分析了频率、载荷、有效半径、振幅等对新型三叉式万向联轴器润滑时压力、油膜厚度的影响。综上所述,联轴器润滑研究成果以线接触为主,少部分点接触考虑的条件较少,与实际情况相差较大。新型三叉式万向联轴器的滑块与滚珠相接触,相当于点接触,就以上工况,本文主要研究在考虑滑块粗糙度情况下润滑油点接触的等温润滑特性。
2 新型三叉式万向联轴器滑块滚珠润滑模型
三维模型如图1所示。
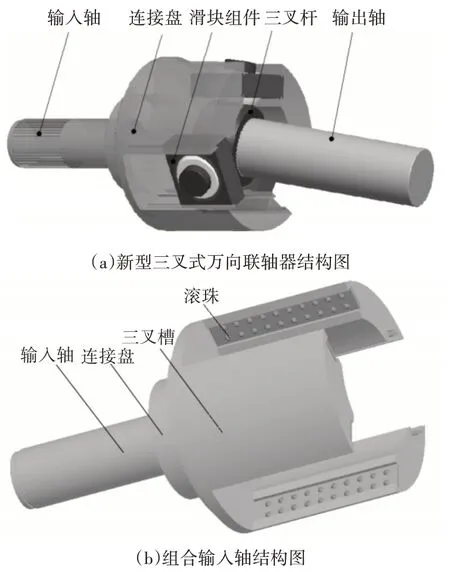
图1 新型三叉式万向联轴器结构及部件图
新型三叉式万向联轴器主要将直线轴承结构应用到三叉槽内,在滑块与三叉槽之间加有滚珠,变滑动为滚动,从而减小摩擦,并且滑道内加有润滑油,滚珠与滑块之间可以看作点接触[12~13],其接触面积小且载荷大,形成高压区,从而使润滑剂的粘性系数发生变化,接触面发生弹性变形。
简化模型如图2 所示,图中1 表示滑块,2 表示滚珠。
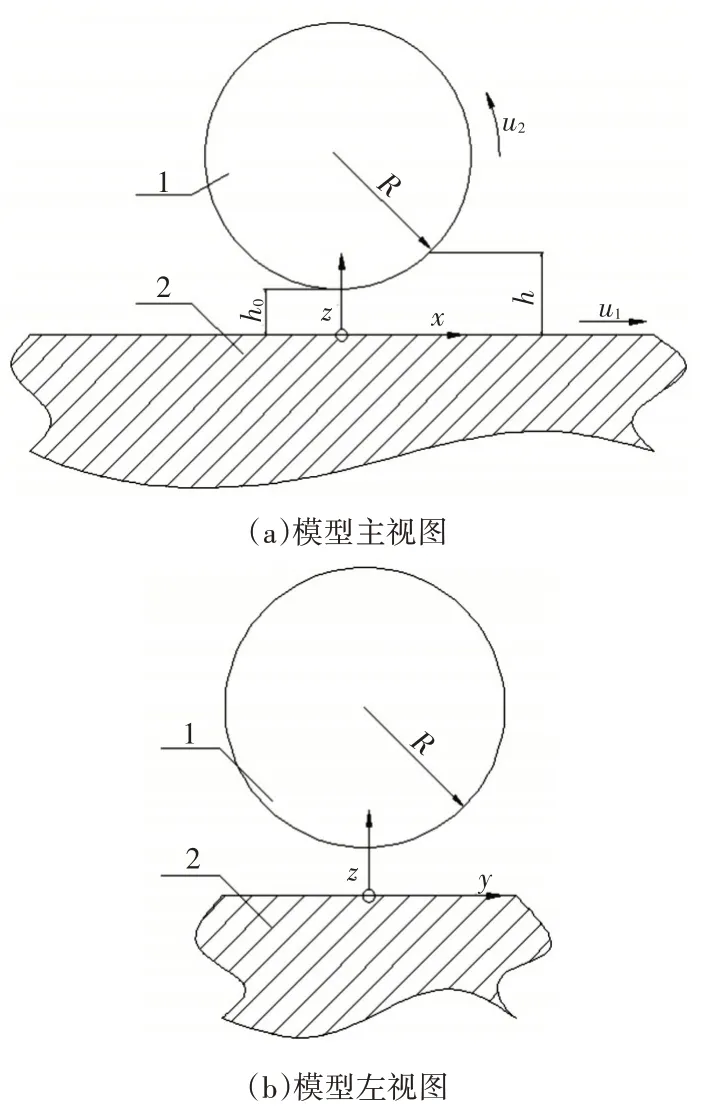
图2 新型三叉式万向联轴器滑块滚珠润滑简化模型
其中,滚珠为球体,坐标系原点位于滚珠的球心在滑块上的投影点,x方向位于滑块表面指向三叉槽轴线方向,y方向位于滑块表面垂直于三叉槽轴线方向,z方向垂直于滑块表面,指向滚珠球心,滑块沿三叉槽轴线来回移动,也就是沿x方向移动。
3 粗糙表面等温弹流润滑分析
3.1 弹流润滑方程
给出二维Reynolds方程[14]研究点接触润滑,表达式为
式中:r为润滑油的密度,kg/m3;h为润滑油粘度,Pa·s;h为膜厚,mm;us为相对速度,m/s;2us=u1+u2(u1、u2分别为滑块、滚珠的速度)。
膜厚方程为
式中:h0为最小膜厚,mm;v(x,y)为弹性变形;r(x,y)为粗糙度变形;r(x,y)=DAsin(2πx),DA 为粗糙度幅值,mm。考虑到滑块只沿x方向移动,因此表达式只在滑块x方向采用正弦函数。
式中:p(s,t)为压力函数,包含了滚珠和滑块的综合变形;E为综合弹性模量,Pa,其表达式为
式 中:E1=210GPa,E2=210GPa,v1=0.3,v2=0.3,E≈230GPa。
粘压方程采用Roelands模型,表达式为
其中,η0为初始润滑粘度,Pa·s。
密压方程为
其中,p为压力边界,GPa,p(x0,t)=0、p(xe,t)=0、p≥0。
载荷方程为
3.2 量纲一化方程
压力量纲一化P如式(8)所示。
其中:PH为最大接触压力,GPa。
膜厚量纲一化H如式(9)所示。
式中:Rx为接触面在x轴方向的综合曲率半径;a为接触区半径长度,mm。
量纲一化X和Y如式(10)所示。
粘度量纲一化h*如式(11)所示。
密度量纲一化r*如式(12)所示。
其中:ρ0为初始润滑油密度,kg/m3。
载荷量纲一化W如式(13)所示:
3.3 差分方程
Reynolds方程离散形式为
简谐粗糙度膜厚方程[15]离散形式为
其中:为弹性变形的刚度系数。
载荷方程离散形式为
3.4 初始条件
润滑油应用P100型号,参数如表1所示[16]。

表1 P100润滑油参数
利用多重网格法进行计算,节点数N=65×65,量纲一化处理X方向起终点坐标为X0等于-2.5 和XE等于1.5;量纲一化处理Y方向起终点坐标为Y0等于-2.0 和YE等于2.0;经具体测量,R取0.002m,Us为1.0m/s。
4 简谐粗糙度下等温弹流润滑分析
利用差分法将以上方程离散处理[17],利用Reynolds 差分方程进行迭代。精度设置为10-4,利用Matlab软件进行仿真绘图。
4.1 考虑粗糙度幅值对油膜的影响
根据式(3)和润滑理论可知,油膜在滑块和滚珠之间的表面形成,表面由于粗糙度幅值不同而高低不平,因此油膜也会沿高低不平的表面形成,坐标系位于粗糙度为0 的部位,现在的膜厚相当于原膜厚加上或减去粗糙度幅值,而膜厚与压力之间存在Reynolds 方程的关系,从而使压力改变,而压力又会改变初始膜厚,因此,粗糙度幅度主要影响膜厚的厚薄来起作用。
考虑粗糙度时,用简谐粗糙度进行考察[18],首先考虑粗糙度的幅值,对滑块具体测量后,发现粗糙度幅值在0.01mm 和0.04mm 之间,频率在1Hz 和5Hz 之间,为了方便分析,分别使DA 取0.01mm、0.02mm 和0.03mm,频率1Hz,观察膜厚和压力的变化情况。简谐粗糙度在X方向呈现正弦变化,在Y方向上没有变化,在整个取值范围内,共有4 个周期,以0 为波动中心,幅值分别为0.01mm、0.02mm和0.03mm。
膜厚变化如图3所示。

图3 随简谐粗糙度幅值变化的膜厚曲线图
如图3 所示,从整体来看,考虑粗糙度的膜厚变化量与原膜厚变化量相似,膜厚呈现四周厚,中间薄的状态。如图3(a)所示,X方向接触区膜厚几乎不变,在接触区尾部时,膜厚略有下降,出接触区,膜厚上升;如图3(b)所示,膜厚呈对称分布,进入接触区时,膜厚明显上升,接触区较平稳,离开接触区时,膜厚明显下降,然后快速上升。最小膜厚位于接触区尾部。由此可知,随着粗糙度幅值从0增大到0.03mm时对滚珠与滑块之间的油膜产生一定的波动影响,接触区中心膜厚随着粗糙度的幅度变大而变厚,接触区边缘几乎不变,说明在实际应用当中,粗糙度的幅值是值得考虑的因素。
压力变化如图4所示。
如图4 所示,从整体来看,考虑粗糙度的压力变化量与原压力变化量相似。接触区域呈现二次函数曲面的形状,在接触区尾部时,产生二次压力峰,接触区外压力为0。如图4(a)所示,X方向压力曲线近似为二次曲线,接触中心前部压力随着幅值增大而变大,并且出现明显降低和升高的突变,而在接触中心后部,压力越来越小,在离开接触区时出现二次压力峰值;如图4(b)所示,Y方向压力整体近似于二次曲线,压力对称分布,随着粗糙度的增大,接触中心区压力越来越大,并且曲率越大,最大压力位于接触中心处。由以上分析可知,随着粗糙度幅值从0增大到0.03mm,滚珠与滑块之间的润滑油压力也随之增大,压力的改变又会改变初始膜厚,因此,粗糙度幅度主要影响膜厚的厚薄来起作用。

图4 随简谐粗糙度幅值变化的压力曲线图
4.2 考虑粗糙度频率对油膜的影响
对粗糙度的考察,除了粗糙度的幅值,还有变化频率,根据式(3)和润滑理论可知,表面由于粗糙度频率不同而波动快慢不同,油膜也会随不同波动频率的表面形成,膜厚随粗糙度频率的增快而波动变快,膜厚通过Reynolds 方程使压力波动频率改变,而压力又会对初始膜厚反馈,从而影响膜厚数值大小,继而使压力幅值变化。因此,粗糙度频率通过改变膜厚的波动频率来影响润滑特性。
使 频 率 为1Hz、2Hz、3Hz 和4Hz,幅 值 为0.02mm,观察膜厚和压力的变化。简谐粗糙度在X方向呈现正弦变化,在Y方向上没有变化,在整个取值范围内,分别有4、8、12 和16 个周期,以0 为波动中心,幅值为0.02mm。
膜厚变化如图5所示。
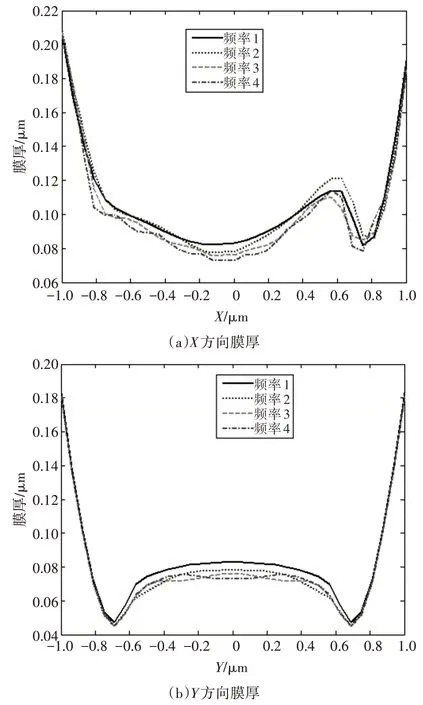
图5 随简谐粗糙度频率变化的膜厚曲线图
如图5 所示,从整体来看,考虑粗糙度频率的膜厚变化量与原膜厚变化量相似。如图5(a)和5(b)所示,在X方向,接触区中心膜厚随着粗糙度的频率增加而逐渐减小,接触区末端边缘膜厚在频率为2Hz时增大,频率为3Hz和4Hz时减小,并且粗糙度频率增快,膜厚波动更频繁,Y方向膜厚对称分布,随着频率的增加,膜厚数值减小,且波动更频繁。产生该现象的主要原因是表面由于粗糙度频率不同而波动快慢不同,油膜也会随不同波动频率的表面形成,膜厚随粗糙度频率的增快而波动变快。
压力变化如图6 所示。从整体来看,考虑粗糙度频率的压力变化量与原压力变化量在Y方向相似,在X方向波动较为明显。由图6(a)观察,随着粗糙度频率的增加,X方向上压力以原曲线为中心的波动次数越来越多,并且幅度越来越大,二次压力峰成为最后一次波动;如图6(b)所示,接触区压力对称分布,且随着粗糙度频率的增加,接触区压力来回波动,中心区最大压力变化不大,但曲率变大,逐渐变成凸起。随着粗糙度频率从1Hz增加到4Hz 时,滚珠与滑块之间的油膜的压力波动也随之增大,压力又进而影响联轴器传动的润滑特性,因此,粗糙度频率也是分析润滑特性值得考虑的因素。

图6 随简谐粗糙度频率变化的压力曲线图
5 结语
1)在点接触等温弹流润滑时,随着简谐粗糙度幅值的增大,接触区中心膜厚随之变厚,压力波动越来越大,二次压力峰值几乎不变;随着简谐粗糙度频率的加快,接触区中心膜厚随之变薄,波动越来越频繁,压力以原曲线为中心的波动次数越来越多,并且幅度越来越大。
2)粗糙度的幅值、频率都会影响新型三叉式万向联轴器的润滑特性,加工过程中要控制粗糙度,应该减小粗糙度幅值和频率,从而优化润滑特性,同时让滚珠安装到位,使滚珠滚动顺畅。本结果为新型三叉式万向联轴器应用在汽车传动系统中减轻摩擦磨损提供理论依据和技术支持。
