狭义相对论时空效应的教学研究

李慧生，姚林红，高燕琴，薛锐

（中北大学 理学院，山西 太原 030051）

狭义相对论的时空特性是大学物理中的重点内容.由于日常生活所能接触到的都是远低于光速的运动物体，所以初学者对于狭义相对论所揭示的时空特性往往既感到神奇又不甚理解.因此，关于狭义相对论特性的教学研究也一直备受关注[1-6].在解决相关问题时也常常忽略时间延缓和长度收缩这2 个公式背后的应用条件，而得到错误的结论.这里构造典型例题，对之求解和分析有助于学生掌握应用时间延缓和长度收缩公式解决相关问题需要注意的条件，同时也可以让学生理解洛伦兹时空变换规律是狭义相对论时间延缓和长度收缩等时空效应的根源.

1 例题分析与求解

例1一静止长度为l0的火箭以恒定的速度u相对于地面向右运动（见图1），从火箭头部发出一光信号，问在地面上观测光信号从火箭头部到达尾部所需要的时间.

图1 例1 配图

解法1欲求地面上观察事件需要的时间先求火箭上观察需要的时间，根据光速不变，把火箭设为s′，地面设为s系，在火箭上测得的时间为，再根据时间延缓公式[7]38地面上测得的时间为

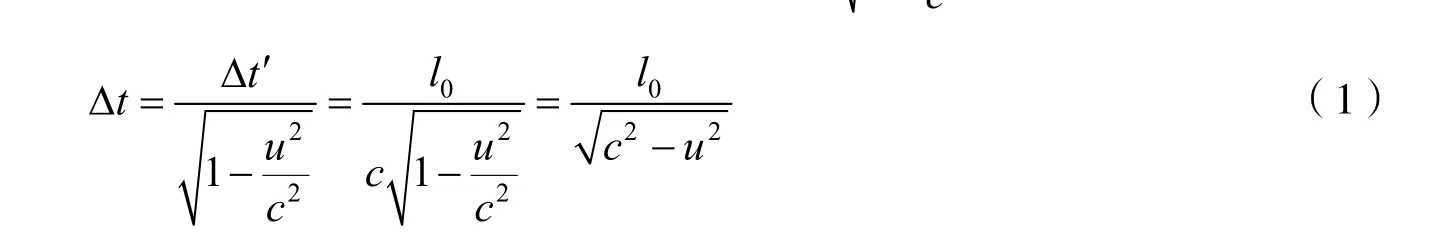
解法2根据长度收缩公式[7]39，地面上的人测得的火箭长度为，再根据光速不变地面上的人测得的光信号从船头到船尾的速度为c，在光信号飞向船尾的同时飞船也在飞行，地面上测得飞船飞行的速度为u，这是一个相遇问题（后面对此有详细的解释），因此地面上的观察者测得的时间为

方法1 和方法2 分别利用时间延缓和长度收缩公式计算，但是却得到了不同的结果.这说明其中至少有一种方法是不正确的.对这个问题稍加分析，在火箭上测得的光信号从头部到达尾部的时间，和火箭参考系下的火箭长度l0都是没有问题的.在教学中发现有很多学生认为式（2）是错误的，这些学生认为式（2）中由洛伦兹长度缩效应可得地面上的观察者测得的飞船长度为，但是除以的速度c+u明显大于光速，由于光速不变原理，物体的速度不可能大于光速，所以认为式（2）是错的.那么到底哪个是正确的呢？

其实欲求地面上测得的时间Δt，完全可以利用洛伦兹变换式来求，分别用表示在飞船参考系观测到光信号从船头发出和到达船尾2件事的时间和地点，用（x1，t1），（x2，t2）表示在地面参考系观测到光信号从船头发出和到达船尾2件事的时间和地点.利用洛伦兹变换公式有

式（3）（4）相减得

对比式（1）（2）（6）的结果可以发现，式（2）的结果与式（6）的结果相同.由于利用洛伦兹变换解决问题具有普适性，因此式（2）利用长度收缩的计算是正确的，而式（1）利用时间延缓计算是错误的.

2 结果分析

假设Δt时间后光信号到达船尾（见图2），由于在tΔ 时间内光和飞船相向运动，在地面看来飞船船速为u，光信号速度为c，这是一个相遇问题，因此式（2）分母中自然要出现光速加船速c+u，这与光速不变并不矛盾.

图2 光与飞船船尾相遇示意图

3 结论

同样的分析由洛伦兹变换式可以得到

由于对于相对观察者运动的物体只有在Δt′=0时，测得的长度才是物体长度，也就是说运动物体长度Δx′的测量，必须确保在Δt′=0的情况下进行.而相应的定义相对静止的情况下测得的长度为固有长度，即式（7）中的Δx为固有长度l0，式（7）就转化为长度收缩公式

4 结语

通过一个典型问题的多种求解和分析，指出时间延缓公式和长度收缩公式都是洛伦兹时空变换式在特定情况下的结论.相对于洛伦兹变换式的普适性，时间延缓公式和长度收缩公式在使用时有一定的条件，抓住固有时、固有长度是利用它们解决问题的关键.同时，指出固有时的严格表述是同一地点发生的2 件事的时间间隔.另一种表述：相对静止的时钟测得的时间只是一种近似表示，在某些极端情况下并不成立.