质量位移效应对部分相干源关联函数的影响

石萌萌，宋秀丹，李淑侠

（黑龙江大学 物理科学与技术学院，黑龙江 哈尔滨 150080）

为探索核-核碰撞早期形成的极端系统，高能重离子物理学应运而生.由于无法直接用肉眼观测重离子碰撞的具体过程，现阶段只能通过末态粒子观测量的分析来反推其碰撞细节.其中，HBT 关联函数是探寻高密高压下极端系统特性的有效手段.HBT 关联函数最早出现于上世纪50 年代，为了测量天体尺度，Harbury、Brown 和Twiss 利用强度干涉仪吸收到的光子数构建出关联函数，因此发明强度干涉学分析方法，这种方法称为HBT 关联函数[1].1960 年，Goldhabor[2]等首次将HBT 关联应用于高能物理实验中.此后，这种方法被作为一种探索粒子发射源时空结构的有效手段.

当2 个重核离子相互碰撞时，粒子被冲击压缩，在碰撞核交叠区域产生极端高温高密媒介系统，媒介系统经历膨胀冷却后射出大量自由粒子到达探测器[3-4].尚未冻出媒介系统的粒子称作准粒子，准粒子在飞离反应区之前一直与媒介系统相互作用，这种相互作用使准粒子质量相较于真空中自由粒子质量产生变化，这一过程叫做质量位移效应[5].质量位移效应的存在会对末态粒子的关联函数产生影响，这将有益于分析粒子发射源内部媒介系统的动量分布和状态方程.在以往讨论相对论重离子碰撞的过程中，一般选取混沌源作为粒子发射源.但随着碰撞能量的不断增强，片面地将粒子发射源看作是完全混沌的已不再符合实验事实.2013 年，ALICE 合作组在的Pb-Pb 碰撞中，发现粒子的关联性受到了明显抑制，与完全混沌的粒子发射源相比，这种抑制使得粒子关联函数在低动量区存在23%±8%的相干发射分数[6-7].2015 年 Wong[8]等研究了静态球对称谐振子平均场中全同π介子气体的玻色-爱因斯坦凝聚，证明在重离子碰撞中的凝聚现象会导致发射源产生一定程度的相干发射.这些实验事实可以证明若想更精确地描述粒子发射源，还应该考虑一定的相干成分.因此，在部分相干源模型下探寻质量位移效应对两粒子关联函数的影响更能精确地描述粒子发射源的时空结构.本文将在部分相干源模型下讨论包含质量位移效应的关联函数公式.

1 部分相干发射源模型下的两粒子关联函数

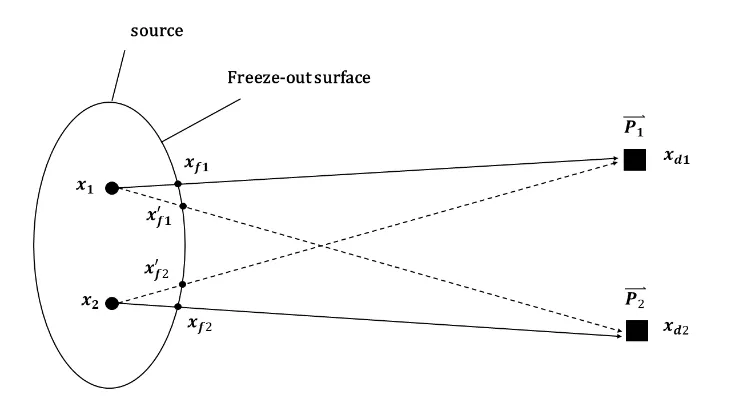
图1 在xd1,xd2处检测到由粒子发射源内发出两粒子的可能路径

对于一个部分相干发射源来说，粒子发射源分布为混沌源和相干源2部分叠加之和，因此在部分相干发射源内，动量为的2个粒子从x1,x2处发出，到x d1,xd2处被探测到，这一过程所产生的总几率振幅为

动量分布P1（→）表示发射源点x发射单个动量为p→的粒子抵达探测点xd的概率，则

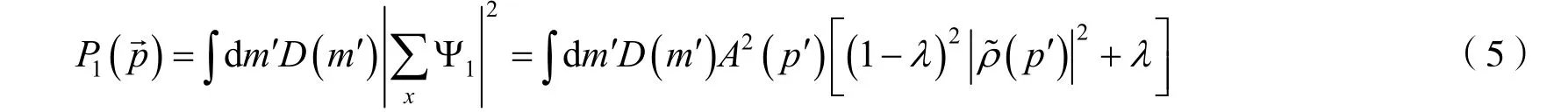
式（5）中的D（m′）是准粒子在媒介系统中的质量分布，该质量分布采用了Breit-Wigner 形式[9].Δm′=m-m′表示准粒子在媒介系统中的质量位移，Γ是介质质量宽度，根据单粒子动量分布可以得到两粒子动量分布为P2（→ ,→）

两粒子HBT 关联函数定义为

将式（5）（6）代入式（7）中，得到两粒子关联函数

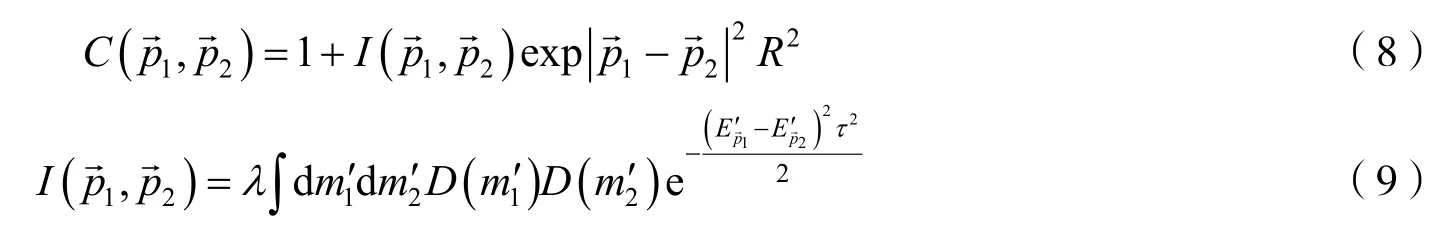
式（9）中的I（→,→）是两粒子的关联强度，由式（9）可得部分相干发射源的两粒子关联强度与粒子的质量位移和粒子发射源的混沌性参量有关.

2 质量位移效应下的部分相干粒子发射源关联函数分析

假定粒子发射源模型为径向膨胀的球壳模型，基于准粒子和自由粒子的质量位移效应，从两粒子关联函数定义出发，两粒子关联强度与准粒子在媒介系统中的质量分布D有关.以Φ粒子为例，计算了两粒子关联强度随着粒子质量变化的关系（见图2）.图2a～d中粒子动量分别取0，300，500，800 MeV/c，图中的3 条曲线分别对应质量宽度Γ为4.26，10，20 MeV/c2时，关联强度与准粒子质量m′的关系.这里取粒子发射源的混沌性参量λ=0.8，源的寿命τ=2 fm/c，真空中自由Φ粒子的质量m=1 019.4 MeV/c2，真空中介质质量宽度Γ0=4.26 MeV/c2[10-11].

图2 不同质量宽度Γ 下Φ 粒子质量与关联强度的关系

从图2 中可以看出，当介质质量宽度Γ=4.26 MeV/c2时，两粒子关联强度具有典型的双峰结构，这是因为当Δm=0时，两粒子关联强度为1，当Δm∝±∞时，两粒子关联强度值也会趋于1，于是就会出现这种双峰结构.图中粒子发射源的混沌性参量λ取0.8，相应的两粒子关联强度的值小于1.当动量一定，随着介质质量宽度Γ逐渐增强，双峰结构的峰值缓慢增加，即粒子动量一定时，双峰结构的峰值随介质质量宽度Γ的变化而变化.通过比较图2 中a～d，还发现两粒子关联强度随着粒子动量的增加而增大，这是因为当粒子动量增加时，粒子能量增加，两粒子的关联强度也随之增加.但是准粒子质量m′对两粒子关联强度的影响，存在于介质质量分布D（m′）中.当准粒子质量m′增加时，关联强度也随之增加，但当准粒子质量m′等于自由粒子质量m时，即粒子质量位移Δm=0时，介质质量分布D（m′）的大小仅取决于介质质量宽度Γ，对应图像中出现的“谷底”.

图3 不同混沌性参量λ 下D 0粒子和Φ 粒子动量与关联强度的关系

根据关联强度式（9），当粒子发射源的混沌性参量达到最大值λ=1时，两粒子关联强度最大；当λ=0时，两粒子关联强度为0.从图3中可以看出，两粒子关联强度都随着混沌性参量λ的增加而增大，在大动量处，Φ粒子的关联强度随着混沌性参量λ的增加而显著增大，所以Φ粒子的关联强度对粒子发射源的混沌性参量λ还是很敏感的，这可以从式（9）中的关联强度与混沌性参量λ的比例关系得出，但D0粒子和Φ粒子受到介质质量分布的制约，这种变化并不是线性的.

3 结论

本文采用强度干涉学的分析方法分析粒子质量位移效应对两粒子关联强度的影响，得到含有粒子质量位移效应的两粒子部分相干发射源关联函数公式.当Φ粒子的介质质量宽度取真空质量宽度ΓΦ=4.26 MeV/c2时，两粒子关联强具有典型的双峰结构.当Δm=0时，关联函数的值为1；当Δm∝±∞时，关联函数的值也会趋近于1，于是形成了这种双峰结构.当粒子动量一定时，随着介质质量宽度Γ逐渐增强，双峰结构的峰值缓慢增加，即粒子动量一定时，介质质量宽度对双峰结构产生了影响.在媒介系统的质量分布D中，介质质量宽度大小相对于具有较宽质量分布的Φ粒子来说影响比较小.两粒子关联强度还与粒子发射源的混沌性参量λ有关，计算结果表明2 种粒子关联强度都随着混沌性参量λ的增加而增大，这表明在大动量处，Φ粒子的关联强度随着混沌性参量λ的增加而显著增大，所以Φ粒子的关联强度对粒子发射源的混沌性参量λ还是很敏感的.因此，只要确定粒子动量的大小，就能得出在不同介质质量宽度下的HBT 关联函数曲线，将这样的图形称为标准图.将实验数据与标准图比对，找到与实验数据最为相近的一条曲线，这条曲线相应的介质质量宽度和混沌性参量就可以看作是粒子发射源的介质质量宽度和混沌性参量.本文只讨论HBT 关联函数其中一方面的应用，但HBT 关联函数的应用不止于此，利用HBT 关联消失现象探测强子冻出信号和探测喷注现象都说明HBT 关联函数在高能重离子碰撞中的重要应用.