基于尺度特征融合的随机森林日供水量预测模型

白 云，陈国强

(1.重庆工商大学 管理科学与工程学院，重庆 400067； 2.重庆市北碚区住房和城乡建设委员会，重庆 400700)

1 研究背景

城市供水量预测在水管理和调度中起着重要作用。尤其是面对城市缺水，迫切需要精确的供水量预测模型用于水资源规划和管理。目前供水量预测模型有很多，如多元线性回归模型[1]、人工神经网络(ANN)[2]、关联向量机[3]、支持向量机(SVM)[4]以及灰色模型[5]等。然而此类单回归器的建模训练可能会出现过拟合现象，所以集成学习[6]提供了一个思路。Breiman[7]将他在1996年提出的Bagging集成学习理论与Ho[8]在1995年提出的随机子空间理论结合而提出随机森林(random forest,RF)。RF是随机选择多个树的特性集的子集，以此构造成簇的森林，利用每棵树投票打分的模式进行决策分类或回归。RF模型具有执行速度高、计算量小、计算精度高等特点，可以处理非线性、交互、非稳态的问题。与其他模型相比[9-10]，RF体现出明显的优越性。

由于日用水量的非平稳性和耦合特征的复杂性，在应用预测模型前，如果对原始时间序列进行尺度特性提取，将有助于提高预测精度。例如，Odan等[11]将ANN和傅里叶级数组合、Shafaei等[12]将小波分解与自适应回归模型组合、佟长福等[13]构建小波组合模型、郝丽娜等[14]提出小波广义回归神经网络耦合模型。这些基于尺度分解的模型结果均表明其预测精度优于单一模型，也表明小波变化在时域和频域方面具有较强的尺度特性提取能力[15]。

基于以上介绍，本文提出基于尺度特征融合的随机森林模型(SF-RF)对城市日供水量开展预测。首先，利用离散小波变换对原始时间序列进行尺度转化和细节特征提取；然后，根据各尺度信息的混沌特性构建RF模型的输入输出结构，其中对于包含随机因子最多的高频信息予以舍去；最后，叠加各尺度的结果获得最终预测值。将预测结果与RF、经典神经网络(FFNN)以及融合模型(RF-FFNN)的预测结果进行对比分析。

2 模型介绍

2.1 离散小波变换

小波变换是由一系列的数学函数构成，它将非平稳时间序列分解为多个子序列，利用基波(如本文使用的Daubechies小波基)在不同的时频域上进行转化。离散小波变化(DWT)因实现简易且计算量小而被广泛应用[16]。图1为DWT分解示意图(以2层分解为例)，其中时间序列x=[xi|i=1, 2,…,N]，N代表时间长度。

图1 DWT分解示意图Fig.1 Decomposition of discrete wavelet transformation

根据图1，对时间序列x进行采样，利用低通滤波器LP获得近似因子ak，利用高通滤波器HP获得细节因子dk，则原始时间序列x的DWT转换形式为

式中k=1, 2, …,K代表分解尺度。

2.2 随机森林模型

随机森林是由一系列决策树组成，每棵树从训练数据集中随机抽样单独构建，并用“if-then”的策略来更新替换，从而形成自上而下的树状结构[17]。决策树使用在所有输入特征值中最好的特性值进行分裂，并在每个终端节点处，自上向下添加随机预测节点。即输入变量对应于根和输出可以描述实际的树的叶子[18]。从本质上讲，RF方法是基于分裂节点的特定区域搜索最佳值的预测模式。RF有两个参数，即Ntree(树木生长的数量)和s(在每一个节点上随机取样的变量数)。随机森林回归执行程序如下：

(1)在原始数据集中进行Bootstrap采样。

(2)生成初始回归树并更新Bootstrap采样：每个节点上，随机选取样本的输入特性，并在这些样本特性中选择最佳的分割，而不是在所有输入特性中选择最佳的分割。

(3)利用out-of-bag理论计算误差并评估更新后的样本误差值。

2.3 基于尺度特征融合的随机森林模型

基于尺度特征融合的随机森林模型(SF-RF)流程如图2所示。

图2 SF-RF预测模型流程Fig.2 Flowchart of the proposed SF-RF model

建模步骤总结如下：

第一步，日供水量时间序列分组，80%数据作为训练集，20%作为测试集。

第二步，对不同数据集分别执行DWT程序，此程序在Matlab 2018a中执行。

(1)本文选择’db4’小波。

(2)小波变换过程中，尺度K过大原始数据失真，而尺度过小近似部分中包含较多随机事件或噪声。本文采用实验法确定。

第三步，对各尺度因子序列分别建立RF回归模型。

(1)对于第k个细节因子序列，其输入为[dk(i-τ), dk(i-2τ), …, dk(i-(m-1)τ)]，期望输出为[dk(i)]。类似的，第K个近似因子序列的输入-输出结构为[aK(i-τ), aK(i-2τ), …, aK(i-(m-1)τ); aK(i)]。其中，m为嵌入维数，τ为延迟时间。本文采用C-C法来确定[19]。

(2) RF模型由Matlab工具箱实现，其中两个主要参数Ntree和s由经验值确定[20]。

第四步，利用测试集数据和训练好的各尺度RF模型，用来预测下一时段各因子序列。

第五步，根据式(1)，线性融合各尺度特征的预测值，则输出最终结果，即

(2)

式中字母带有符号“∧”代表预测值。

3 应用实例

3.1 数据描述

本文研究数据来源于重庆某水厂，该水厂建设于2011年，核定供水能力为20万t/d，主要供给居民生活用水和工业用水。2013年第一个方向的供水管网正式使用，第一方向的日用水量数据从2013年1月21日至2016年1月20日，共1 095个数据。历史记录见图3。

图3 原始数据集Fig.3 Historical records

历史数据的统计学特性见表1。根据最小值、最大值和均值统计，可以得出训练集包含了测试集中所有信息，说明数据分组是合理的。另外，峭度值均>3(一般的，正态分布的峭度值为3)，说明原始数据中大幅值的概率密度增加，幅值的分布偏离正态分布，体现出数据演变的复杂性。

表1 供水量数据的统计学特性Table 1 Statistical characteristics of water supply data

3.2 评价指标

本文采用2个指标进行模型评价，相关系数(R)和标准均方误差(NRMSE)。根据表1中统计值，数据波动范围较大，为了便于不同数值区间的误差比较，采用标准化的均方误差。

(1) 相关系数的表达式为

(3)

式中x带有符号“-”代表平均值。

(2)标准均方误差的表达式为

(4)

4 结果和讨论

4.1 预测结果

根据SF-RF建模步骤，训练所得模型参数见表2。

表2 模型参数设定汇总
Table 2 Definition of model parameters

建模环节参数设定尺度分解(DWT)’db4’母波, K=4特性重构(C-C)a4(m=3, τ=25), d4(m=13, τ=6), d3(m=19, τ=4), d2(m=6, τ=7), d1(m=3, τ=4)回归建模(RF)Ntree=1 000, s=m/3 (即a4取1,d4取4,d3取1,d2取2,d1取1)

根据表2模型参数设定，对测试集(2015年5月27日到2016年1月21日)进行预测，结果见图4。

图4 各尺度随机森林模型预测结果Fig.4 Forecast results using RF model in each scale

由图4可知，近似序列a4的预测效果最好，预测趋势完全模拟了真实演变。细节序列的预测表现出如下规律，即随频率的增大，预测效果变差(尤其是在峰值点)。例如，细节序列d4预测趋势与观察序列一致，但随着频率增高，细节序列d1预测能力在极值突变处表现最差。

近似序列a4可以看成是原始序列的趋势提取项，其幅值是最大的，所以是影响预测精度的重要尺度特征。细节序列d1的高频信息含有过多噪声(真实系统中的随机事件干扰导致)，可以看成是原始序列的随机提取项，而尺度越小(频率越高)预测精度越低，所以在尺度特征融合时不考虑细节序列d1的预测结果。此处理既减少了高频噪声信号的干扰，也尽可能保留了原始时间序列的有效信息。

图5(a)为SF-RF模型的最终预测图，与观测值相比，其趋势、拐点、峰值等均能够较好拟合，NRMSE=0.056。图5(b)为预测值与观测值的散点图，两组数据呈现聚集趋势，R=0.913。与全尺度特征的融合结果相比(不删除d1尺度，NRMSE=0.067，R=0.87)，不考虑高频信号d1的融合策略，对削弱时间序列的随着机干扰有显著作用。然而，SF-RF模型对于极大值的预测也体现出不足，主要原因有以下两个方面：① 高频信息的随机效应，特别是对高峰突变值的预测干扰，通过误差累积影响了尺度融合结果；② 根据文献[19]，m和τ也会受到随机事件的影响(例如，图3中2015年2个突变点)，从而导致模型输入结构的适宜性，即局部相空间特性学习不足影响了映射关联度。整体而言，本文提出的SF-RF模型可以较好地模拟日供水量预测。

图5 SF-RF模型预测结果Fig.5 Forecast results using the proposed SF-RF model

4.2 对比分析

为了比较本文提出的SF-RF模型性能，2个独立模型RF和FFNN、1个尺度特性融合的SF-FFNN模型对相同数据集进行建模和预测。

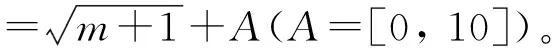
3个对比模型的预测结果见图6。从图6可以发现，尺度融合模型SF-FFNN预测性能优于其他2种独立模型，而与本文提出的SF-RF模型相比，极值拟合效果一般。表3汇总了4种模型的评价结果。

图6 对比模型预测结果Fig.6 Forecast results of comparative models

表3 模型性能评估结果Table 3 Results of model performance evaluation

表3显示：① 尺度特性融合模型(SF-RF和SF-FFNN)预测性能均优于独立模型(RF和FFNN)，说明考虑尺度特征的建模，既减少了随机干扰(高频信息)，又降低了模型学习难度(将复杂单尺度时间序列转变为简单多尺度因子序列)，从而提高了独立建模的预测精度;② 树结构模型(SF-RF和RF)预测性能均优于神经网络(FFNN和SF-FFNN)，验证了RF模型在预测领域的优势。所以，本文提出的SF-RF模型获得了最低的NRMSE值和最高的R值，预测效果最好。

5 结 论

本文提出基于尺度特征融合的随机森林模型来预测城市日供水量。首先，利用小波分解技术将单尺度时间序列的耦合特征转化为多尺度的低、高频特征；然后，利用混沌特性确定各尺度的随机森林映射关系；最后，利用线性融合将各尺度特性预测结果集成。研究表明，尺度特征融合有利于提高预测精度，且预测精度随频率的增加而降低。

对比3种模型，本文提出的SF-RF模型获得了最好的精度，适用于短期预测，为日供水量预测提出了一种新的思路。

本文以去除一个高频信号(细节因子)为融合策略，提高了日供水量预测精度。而如何进一步分解高频信号、识别高频信号中有效特征、构建信息高利用率和高精度的预测模型是下一步的研究方向。