风屏障对简支箱梁桥上风场分布影响的试验研究
2022-03-18邱晓为李小珍谭懿玲李星星
邱晓为, 李小珍, 谭懿玲, 李星星, 肖 军,2,3
(1. 西南交通大学 桥梁工程系, 成都 610031; 2. 中交第二公路工程局有限公司, 西安 710065;3. 中交公路长大桥建设国家工程研究中心有限公司,北京 100011)
列车在大风条件下高速运行时,存在着不容忽视的安全风险,其空气动力性能恶化,不仅升力、横向力迅速增加,还影响横向稳定性,严重时将导致列车倾覆[1-4],因强风导致的列车晚点停运或倾覆事故屡见不鲜[5-6],如日本自1872年有铁路运输以来,共发生了30多起由风引起的列车事故[7-8];中国兰新线自通车以来因大风引起的列车脱轨、倾覆事故多达30多起,吹翻货车100多辆[9];京沪高速铁路沿线每年最高风速大于20 m/s的次数约为19.2次[10],对列车的行车安全性影响较大。相关学者通过将列车空气动力学与系统动力学相结合,对强侧向风作用下车-桥耦合振动系统进行了广泛的研究[11-12],根据强风环境下列车运行安全保障体系[13],与优化列车外形、限制或停止列车运行等措施相比,大风区设置风屏障是提高既有线路列车安全运行的有效措施[14-15]。
沿线路设置风屏障可以为列车创造一个相对低速的局部运行环境,进而有效提高列车行车安全性,国内外学者对风屏障防风性能做了广泛地研究。研究表明:风屏障的遮挡效应主要受其设置高度、设置方向、透风率、孔隙分布等特征参数的影响[16],相较于其他特征参数,风屏障的优化设计往往取决于选择最佳的透风率[17],Seginer[18]通过现场测量结果表明风屏障的透风率是决定其尾流特性最为重要的设计参数;Dong等[19]利用粒子图像测速技术试验方法研究了风屏障后的瞬时速度场,表征了湍流场对风屏障的遮蔽效应有很大影响,优化了风屏障的高度和透风率;向活跃等[20]采用风压排管测试技术开展了风洞模型试验,并结合数值模拟研究了风屏障特征参数对典型线路轨道上方风压分布的影响,分析了风屏障的气动机理。除关注风屏障遮蔽效应下的流场特性之外,相关学者结合列车和桥梁的流场和气动力开展了关于风屏障遮蔽效应的研究,如He等[21-24]基于同步测压技术与数值仿真方法研究了风屏障特征参数对典型列车-桥梁系统气动力的影响,为提高列车在侧风条件下在桥上运行安全性,提出了一种可调节的百叶式风屏障;Guo等[25-26]通过风洞试验分析了风屏障特征参数对车桥系统气动力特性的影响规律,并对风屏障高度及透风率进行了参数化研究,结果表明风屏障能有效地降低了列车上的阻力和弯矩,但提高了桥梁的阻力和弯矩系数。风屏障遮蔽效应随透风率增大的变化趋势并非线性,而是在某一透风率范围内趋于稳定[27],考虑风屏障遮挡效应下的平均风速及湍流特性,Hagen等[28-30]通过现场实测、风洞试验、数值模拟等方法研究表明风屏障最佳透风率约为0.3或0.4。
线路构造形式差异对风屏障的防风效果影响较大,相较于平地,桥上运行的列车对侧风作用更加敏感,其原因在于:由于桥梁的存在改变了列车横截面的纵横比,进而改变横风作用下列车周围及列车表面的压力分布情况[31],具体地,桥上列车背风侧漩涡尺寸及数量都大于平地情况,致使列车背风侧负压区较大,导致桥上列车侧力和倾覆力矩较大[32],而明确桥梁轨道上方风场分布特性是进行车辆气动荷载优化的前提。高速铁路线路中的简支箱梁结构在桥梁总里程中所占比重较大,以京沪高铁为例,正线桥梁244座,总长1 061 km,其中最常用的跨度32 m双线整孔简支梁共计27 973孔,全线简支梁桥总长搭956 km,占桥梁总里程的90%以上[33]。本文针对高速铁路典型跨度32 m预应力混凝土简支箱梁为研究对象,采用风洞试验的方法,考虑风速、湍流强度等影响因素,采集了轨道中心不同桥面高度处的风场信息,通过引入变异系数开展非一致性分析,并系统研究了风屏障对桥面风场的影响规律,得到了典型跨度简支箱梁的风场特征预估剖面图,确定了典型铁路基础结构的等效风速比,为后续风屏障设计及高速列车行车安全性评价提供依据。
1 试验概况及测试方法
试验场地为西南交通大学XNJD-3风洞试验室,其宽、高、长分别为22.5,4.5,36.0 m,风洞空置时的风速范围为0~16.5 m/s,湍流强度1.0%以下,可以模拟JTG/TD 3360-01—2018《公路桥梁抗风设计规范》[34]要求的风剖面、湍流强度、风速谱等。
试验研究的桥梁原型为高速铁路典型跨度32 m预应力混凝土简支箱梁,梁高为3.052 m,梁面宽度为12.6 m。相关研究表明[35]高度为3 m的风屏障防风效果较好,主要考虑透风率的影响,试验模型采用1∶30的几何缩尺比加工制作,桥梁和风屏障的材料类型分别为优质木材和碳纤维板,保证了模型具有足够的刚度和强度。桥梁-风屏障系统风场剖面测试模型截面如图1所示,测试节段模型的长度为3 300 mm,其中风屏障模型厚度为1.5 mm,高度为100 mm,结构的长度和厚度方向与其高度方向的比值分别为33和0.015,因此可以将风屏障结构看作二维障碍物,忽略其顺风边缘对气流分离的影响。风屏障采用双侧布置,考虑透风率15%,30%,45%三种类型,开孔形式为均匀分布的圆孔阵列式,如图2所示。相关研究表明:侧向风在流经桥面时会形成一定厚度的附面层,即距离桥面一定高度范围内,不同高度的风速是不同的。本文以CRH3型列车为背景,沿简支箱梁轨道中心上方布置风场测试点,其中H1~H7为简支梁桥面风场采集区,考虑到风屏障遮挡效应的影响,设置H1~H9为风屏障风场效应采集区,测点布置详如表1所示。
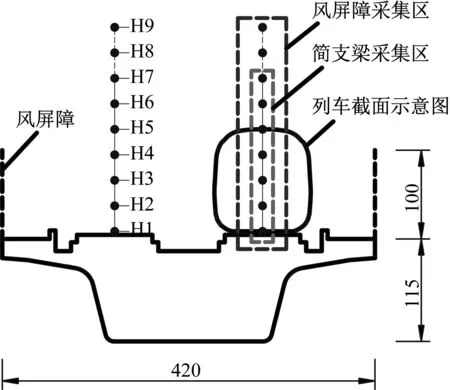
图1 测试模型示意图(mm)

图2 风屏障防风孔示意图(mm)

表1 测点位置
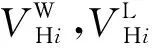

(a) 湍流场布置
2 数据分析
眼镜蛇三维脉动风速测量仪采集三维脉动风速,以u表示来流方向风速,v表示沿桥轴线方向风速,w表示垂直桥面方向风速,总风速V是三个方向风速矢量的合成。本质上随机的自然风可以分解成平均风和脉动风,如式(1)~式(4)所示,以湍流强度Iuu,Ivv,Iww表征测点各方向的脉动风分量,Iuvw表征整体湍流强度,如式(5)~式(8)所示。
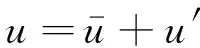
(1)

(2)
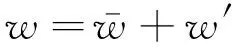
(3)
(4)
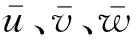
(5)
(6)
(7)
(8)
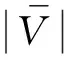
2.1 测点样本分析
为表征桥面风场的三维特性,本文以合成风速V和整体湍流强度Iuvw为研究对象。以迎风侧轨道中心测点H5,即列车高度处风场采集样本为例,均匀来流风速等级为6 m/s,其时程曲线如图4所示,通过统计分析可知:风场在连续的时间域内服从Gaussian分布,风速统计均值与拟合均值基本相等;与来流风速相比,测点风速的离散性及均值较大,说明受主梁遮挡效应的影响,桥面上方存在风速和湍流强度的放大效应,该测点时间平均速度、总体湍流强度分别为7.89 m/s和1.06%,是来流风速的1.29倍和1.46倍。

(a) 时程曲线
2.2 风速对分析测点的影响
为进一步研究不同等级均匀来流风速对迎风侧轨道中心H5测点的影响,基于最小二乘法理论,以线性拟合的方式给出来流风速与H5测点风速之间的变化关系,其拟合直线通过原点,直线斜率即为测点风速与来流风速的比值,如图5(a)所示,可以看出:测试数据的拟合效果较好,其相关系数r约等于1,测点风速与来流风速之间具有良好的线性关系,说明风速比受试验雷诺数效应较小,试验结果可以忽略雷诺数效应的影响;通过统计分析可知测点样本风速比均值的标准误差为4.25×10-3,大于拟合直线斜率的标准误差,说明以样本数据拟合的直线斜率可以相对合理地预测总体数据情况,故该测点的风速与来流风速之比可以取值为1.28,以样本拟合斜率近似作为总体数据的预估值。经统计分析不同等级的来流风速对迎风侧H5测点位置的湍流强度影响较小(图5(b)所示),但总体呈上升趋势,取其多速度等级来流风作用下的均值1.12%作为该测点湍流强度的预估值,其标准误差为0.6‰,预估值的准确性可以满足要求。
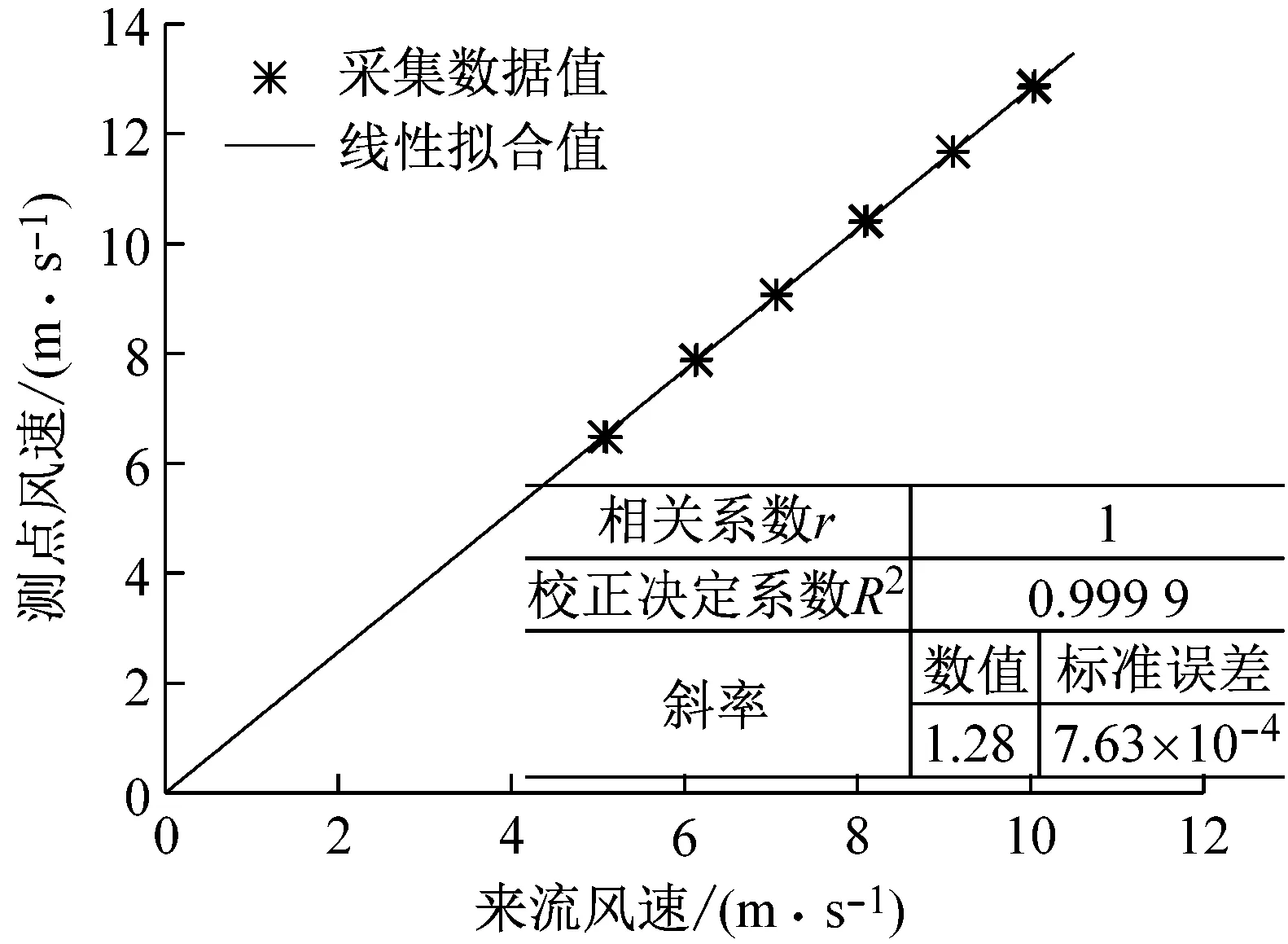
(a) 测点风速拟合
2.3 湍流强度对分析测点的影响
为探究湍流风场对轨道中心H5测点风场特征的影响,本文通过布置尖塔建立湍流风场(详见图3(a)),其湍流强度为9.05%,标准误差0.24%。根据前述数据处理方法,给出轨道中心H5测点风场特征参数图,如图6所示,可以看出:湍流风场中H5测点的测试数据线性拟合效果较好,过原点拟合直线的斜率可以近似看作该测点的风速比;与均匀风场相似,湍流风场中风速对测点的湍流强度影响较小,受简支箱梁遮挡效应的影响,迎风侧H5测点的风速比及湍流强度较低,而背风侧较高;与均匀流场相比,湍流风场下的轨道中心H5测点风速比相对较小,具有显著的折减效应,为结构设计安全性考虑,本文后续主要针对均匀流场进行分析。
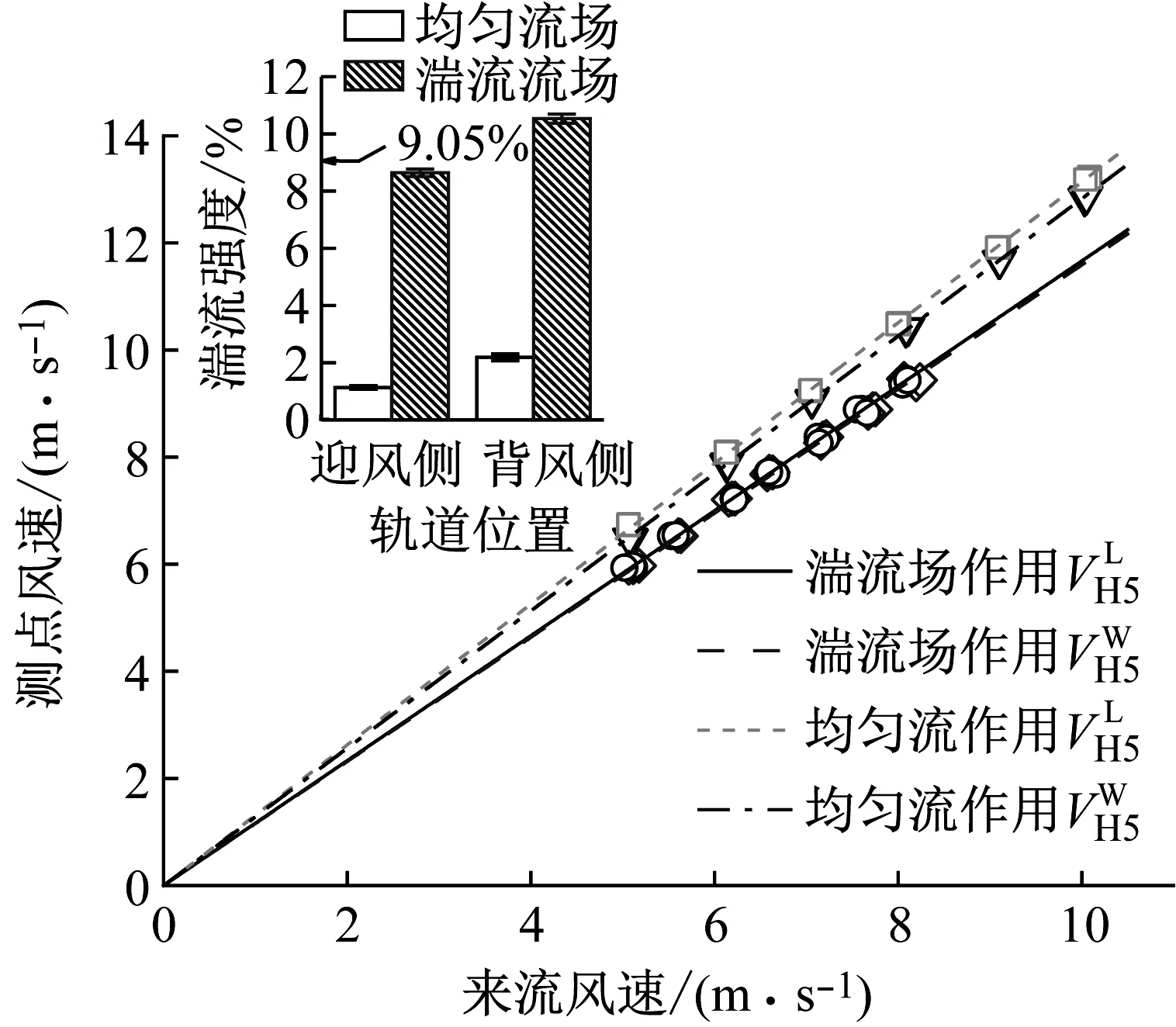
图6 H5测点风场特征参数
2.4 风屏障对分析测点的影响
透风率是风屏障结构设计的重要参数,本文通过设置透风率为15%,30%,45%的三种风屏障结构(详见图2)探究风屏障透风率对轨道中心H5测点风场特征的影响。测点风场特征如图7所示,可以看出:由于屏蔽作用,风屏障显著地降低了屏后的平均风速,其遮挡效率与透风率呈负相关。当风屏障透风率较高时(30%,45%),测点风速与来流风速具有良好的线性关系,过原点拟合直线的斜率可以近似看作该测点的风速比,与裸梁状态相似,其迎风侧的风速比大于背风侧风速比;与其他工况相比,透风率30%风屏障遮挡效应下,桥梁背风侧测点位置的湍流强度较高且随来流风速增大而增大,其风速过原点拟合直线的相关性相对较差,测点湍流强度可能会影响风速比的拟合精度。当屏障透风率较低时(15%),风屏障阻挡了大部风分的来流风,并在两个风屏障之间产生了一个反向流动的区域,测点湍流强度随风速的增大而增大,而测点风速受来流风速影响较小(小于2.1 m/s),试验结果与文献[30]模拟结果相似。

(a) 风速特征
3 典型跨度简支箱梁铁路桥面风场特征分析
为统计分析不同来流风速UO对特征风剖面的影响,以变异系数作为风速非一致性指标,通过引入变异系数CV的方式评价不同测点高度下风速比、湍流强度预估值的合理性,变异系数CV的表达式如式(9)所示。
CV=(σ/μ)×100%
(9)
式中:σ表示来流风速作用下统计变量的标准差;μ表示各来流风速作用下统计变量的预估值。
如前所述,以样本风速的拟合斜率作为风速比总体数据的均值,给出不同测点测试样本的标准差,通过统计分析得到不同来流风速作用下典型跨度简支箱梁铁路桥面风场的非一致性指标。
3.1 简支箱梁桥面风场的非一致性分析
图8(a1)和图8(b1)所示为裸梁状态下桥面特征非一致性指标统计图,可以看出:与其他测点相比,迎风侧H1测点处风速比的变异系数较大,为14.7%,其原因主要在于:① 该测点靠近桥面的附面层,平均风速较小,超出了眼镜蛇三维脉动风速测量仪的采集精度,测量误差较大;② 该测点在不同风速等级作用下的风速比可能受湍流强度的影响较大。除迎风侧H1测点外,总体上典型跨度简支箱梁铁路桥面风场特征参数受来流风速的影响较小,其中风速比变异系数均小于5%,并随测点高度的增加而减小,结果稳定性较高,以样本风速的拟合斜率作为风速比的最终估值较为合理。与风速比相反,湍流强度的变异系数随着测点高度的增加呈增大趋势,各测点的变异系数均小于8%,结果稳定性相对较高。
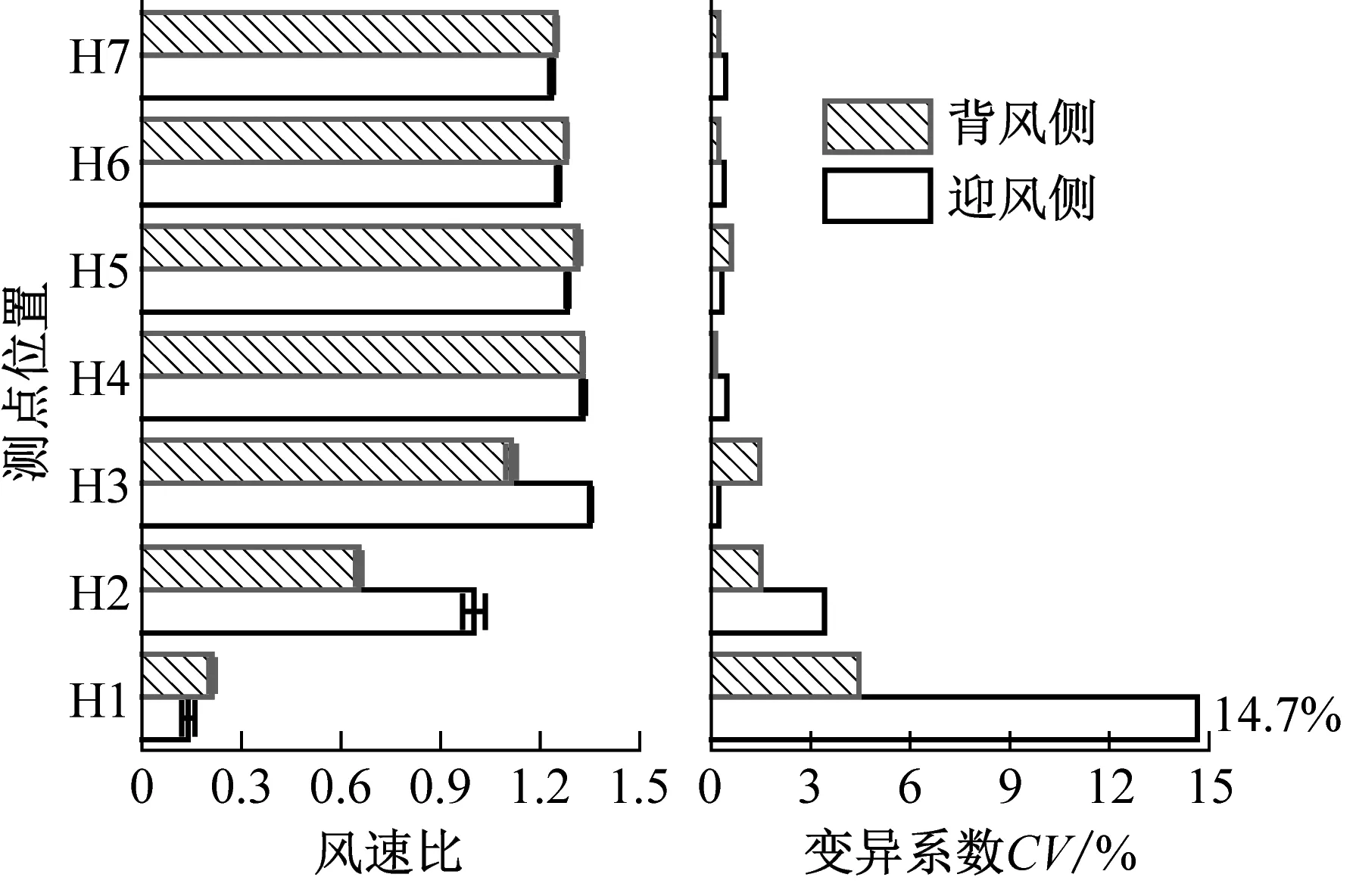
(a1) 风速比非一致性指标
通过前述桥面风场的非一致性指标分析可知各等级来流风速作用下的桥面风场特征参数均值与预估值吻合较好,裸梁状态下桥面特征剖面图如图8(a2)和图8(b2)所示,可以看出:与来流风速相比,桥面轨道中心部分位置的风速增加可达33%;受桥梁绕流的影响,风速比和湍流强度与测点高度有很大的关系,就车辆高度范围内(测点H5以下)风场特征而言,其波动明显,随着测点高度的增加风速呈增大趋势,而风场的湍流强度随着测点高度的增加呈减小趋势;与迎风侧相比,主梁绕流对背风侧轨道中心风场的影响范围较大,迎风侧、背风侧轨道中心风场特征受桥梁绕流影响的主要范围分别在测点H3和H4以下;与迎风侧轨道中心风场分布特征相比,背风侧的风速比和湍流强度随测点高度的变化较为平缓,背风侧风速比拐点(风速比为1的预估测点高度)高度大于迎风侧风速拐点高度。
3.2 风屏障屏蔽作用桥面风场的非一致性分析
为进一步研究风屏障对桥面风场的屏蔽机理,以透风率30%的风屏障试验对象,如图9(a1)和图9(b1)所示统计分析得到屏蔽作用下桥面风场的非一致性指标,可以看出:与裸梁状态相比(图8(a1),图8(b1)),风屏障作用下的桥面风场特征变异系数普遍较大,说明来流风速对预估值的影响较大,仅以单一风速评价屏后流场特性是不合理的;风屏障屏蔽作用下的风速比非一致性指标与其湍流强度有关,风速比的变异系数与湍流强度变异系数呈正相关关系,如H4测点的迎、背风侧湍流强度变异系数分别为18.8%、17.6%,其风速比变异系数分别达到了13.5%、13.6%。

(a1) 风速比非一致性指标
图9(a2)和图9(b2)所示为风屏障屏蔽桥面风场特征参数剖面图,与裸梁状态相比,风屏障有效地降低了桥面的平均风速,风速比拐点向更高点移动,测点结果有一定的离散性。通过前述桥面风场的非一致性指标分析可知:受风屏障的屏蔽作用,各等级来流风速作用下桥面个别测点的风场特征参数,尤其是湍流强度,均值与预估值存在一定的误差,其原因主要有两个方面:一是风屏障显著降低了屏后的风速,受测量仪器精度限值,测量存在误差;另一个方面两侧风屏障之前形成反向流区,增大了流场湍流强度的离散性,进而导致了风速比拟合精度降低。
3.3 桥面等效风速比分析
通常以矩形风剖面等效实际风剖面,等效原则为矩形风剖面和实际风剖面压力总和相等,将等效风速无量纲后即可得到等效风速比,其计算公式如式(10)所示
(10)
式中:r为等效风速比;H为等效高度,即桥面上行驶列车的侧风高度范围(H5测点以内);V为风剖面内风速值;UO为来流风速;δ为风速比。
以车底位置H1作为坐标原点,车顶位置H5作为坐标终点,为减少试验误差,通过前述分析以拟合风速比作为各测点的合理预估值,给出列车横风高度范围内的等效风速比,如图10所示。其中屏蔽桥面的风屏障透风率为30%,可以看出:与迎风侧相比,总的来说背风侧等效风速较小,受主梁遮挡效应的影响,裸梁桥面等效风场具有放大效应,风屏障屏蔽作用下桥面背风侧等效风场的变异系数为10.4%,结果存在一定误差,原因前述已做说明,此处不再赘述;风屏障等效风场折减效应显著,其迎、背风侧等效风速分别裸梁状态下的21.6%和19.4%。
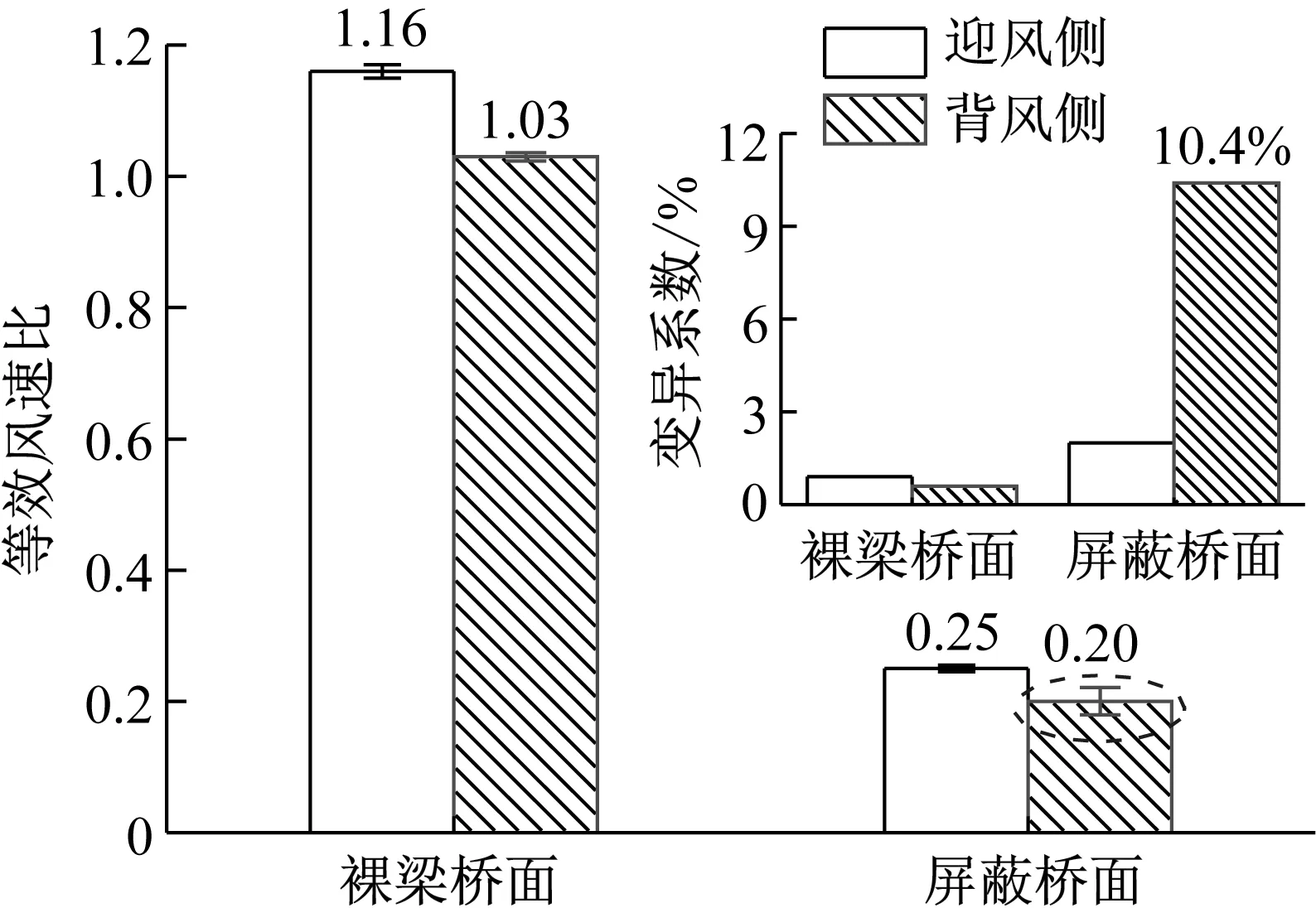
图10 桥面等效风速比
4 结 论
本文采风洞试验的方法探究了横风作用下风屏障对典型跨度32 m预应力混凝土简支箱梁轨道中心风场特征分布规律及影响机理,得到如下结论:
(1) 基于最小二乘法理论对试验数据进行过原点的线性拟合分析,测点风速与来流风速之间具有良好的线性关系,以样本数据拟合的直线斜率可以相对合理地预测总体数据情况。
(2) 均匀风场中受主梁遮挡效应的影响,裸梁桥面等效风场具有放大效应,桥面轨道中心部分位置的风速增加可达32.8%,而湍流风场会弱化这种放大效应。
(3) 与裸梁桥面风场湍流强度相比,均匀风场中来流风速对风屏障屏蔽作用下的桥面风场湍流强度影响较大,其风速比非一致性指标与其湍流强度的变异性相关。
(4) 风屏障可以有效地降低桥面风场的平均风速,风场折减效应与其透风率有关,其中透风率30%的风屏障屏蔽作用下其迎、背风侧等效风速分别为裸梁状态下的21.6%和19.4%,但绕流区的湍流强度会对结果产生一定的影响。
