充液管路轴向多吸振器波动特性研究

吴江海， 孙玉东， 尹志勇， 苏明珠

(中国船舶科学研究中心 船舶振动噪声重点试验室， 无锡 214082)

管路系统广泛应用于船舶、石油、化工等工业领域，充液管路在进行传输液体的同时，也将机械设备等不需要的振动、噪声进行了传播。由于管路大多数为梁状结构，是非常好的弹性波传播介质，有时甚至会放大振动，引起管路的振动疲劳破坏，带来巨大的经济损失。因此充液管路的流固耦合问题引起了国内外学者与工程师的广泛关注[1-4]。

各国学者在考虑管道流固耦合特性和流体压力脉动中，提出了4方程模型、6方程模型、8方程模型和14方程模型[5]。Bürman[6]考虑泊松耦合，提出了充液管道轴向振动四方程模型，Tentarelli[7]后来发展了直管的14方程模型，本文中理论解析模型即采用其中轴向4方程。吸振器是充液管路线谱振动控制的有效手段，王文初等[8]基于阻抗概念，设计一种三向管路动力吸振器，并开展了样机试验；刘天彦等[9]对核反应堆一回路管道设计多频率吸振器；陈果等[10]针对航空发动机导管设计了一种弹簧片式吸振器。

近年来，声子晶体在弹性波调控方面引起了研究人员的广泛关注，部分学者将其引入到充液管路振动控制中来，Yu等[11-13]采用Euler梁与Timoshenko梁模型对充液管路横向局域共振带隙进行了研究。文岐华[14]给出了多振子声子晶体梁的弯曲振动能带结构，并推导了带隙起始截止频率。马建刚等[15]设计了一种具有多带隙特性抑振结构，并将其应用于梁的横向振动试验中。吴江海等[16]研究了充液管路轴向多支撑带隙特性，沈惠杰[17-18]研究了声子晶体带隙在船舶海水冷却管路中的应用。

从上面可以看出大部分论文都是对管路横向振动吸振、局域共振型带隙开展了研究，而对管路轴向振动研究几乎没有。本文从充液管路轴向流固耦合4方程模型出发，采用传递矩阵法，建立管路轴向带多个吸振器动力学耦合模型。本文的研究可为管路系统减振、吸振器的设计与安装提供参考。

1 理论解析模型

1.1 管路轴向传递矩阵

本文充液管路采用Timoshenko梁理论，假设管路中均匀充满液体，无气泡，不考虑流体流动激励，管路与流体通过泊松耦合进行连接。因此充液管路轴向振动方程为

(1)

式中：fz为管壁轴向力；uz为管壁轴向位移；uf为管内流体轴向位移；p为管内流体声压。以上4项为充液管路轴向振动4个自由度。R,h,Ap分别为管路内径、壁厚和横截面积；ρf,ρp分别为管内流体密度和管壁密度；E为管路杨氏模量；μ为泊松比，K*为管内流体体积模量；管道轴向为z方向。

利用分离变量法，假设式(1)的解的形式为

uz(z,t)=Uz(z)ejωt,p(z,t)=P(z)ejωt

uf(z,t)=Uf(z)ejωt,fz(z,t)=Fz(z)ejωt

(2)

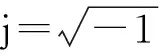
(3)

将式(3)中P(z),Uf(z),Uz(z)消去，只保留Fz(z)得

(4)

因此充液管路轴向振动化为四阶方程，由波动法知，式(4)的解可以写成

Fz(z)=A1ejk1z+A2e-jk1z+A3ejk2z+A4e-jk2z

(5)

式中，k1,k2分别为声波沿管内流体和管壁传播的波数，将(5)代回式(3)得

(6)

其中：

将式(6)简写成矩阵形式

(7)

Vz|z=0=Vz(0),Vz|z=L=Vz(L)

(8)

将式(8)代入式(7)中有

(9)

Taxial=WB(L)WB(0)-1

(10)

1.2 轴向吸振器传递矩阵

吸振器的本质是在安装点对管路系统施加的附加阻抗。易知，刚度为K，质量为M，阻尼为C的轴向吸振器阻抗为

(11)

在管路上吸振器安装位置需满足轴向位移连续与轴向力连续边界条件，因此吸振器的传递矩阵为

(12)

因此管路上布置多轴向吸振器传递矩阵为

T=Taxial*TDVA…TDVA*Taxial

(13)

1.3 计算方法验证

为验证本文计算方法的正确性，对图1所示直管带单个轴向吸振器模型，计算其动态位移响应，并与商用有限元软件计算结果对比。图中管路外径为DN100，壁厚为4.5 mm；管路采用钢材质，杨氏模量E=2.1×1011，泊松比μ=0.3，密度为7 800 kg/m3, 管路长度为2.0 m，整个管路质量为21.06 kg。管路两端为自由边界，在管路中间安装一轴向质量-弹簧振子吸振器，其中刚度为K=1×107N/m，质量Mass=5 kg。在右端P2点施加一轴向单位简谐激励力。

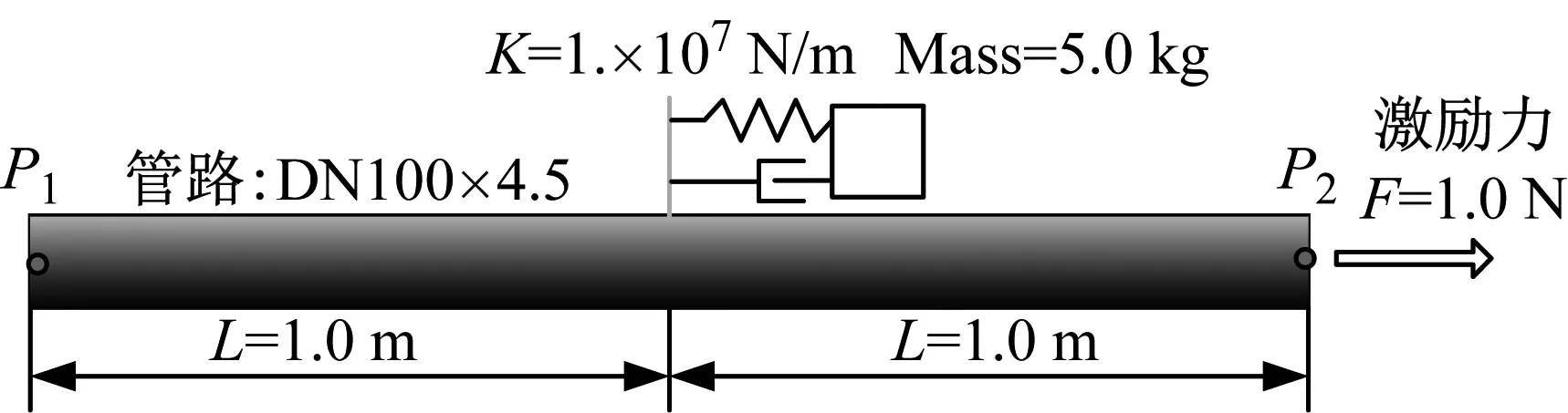
图1 管路轴向计算模型

有限元模型中，管路采用Beam单元，吸振器采用弹簧单元与集中质量模拟，网格尺寸为0.001 m，网格数量为2 000。计算频率范围1～3 000 Hz，满足有限元中单个波长中包含6个单元的计算精度。P1点和P2点的计算位移响应如图2所示。

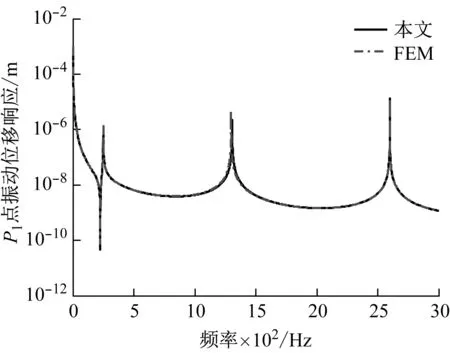
(a) P1

从图2可以看出，本文采用传递矩阵方法计算结果与FEM计算结果完全吻合，证明了本文计算方法的正确性。在图2(a)中出现的反共振峰(225 Hz)即为吸振器轴向共振频率。

本文对图1中所示带吸振器管路系统充水与不充水时，自由边界条件下前5阶固有频率进行了计算，并与有限元计算结果进行对比，如表1所示。不充水时，本文计算结果与FEM计算基本一致，充水时本文计算结果略大于FEM，误差在4%以内，进一步证明本文计算方法的正确。

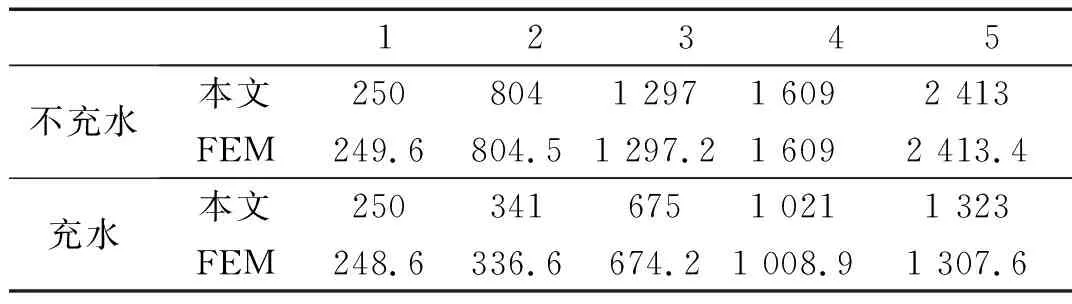
表1 固有频率对比

2 波动特性

结构中的弹性波在不连续点处存在透射与反射现象，对于一无限长管道，轴向吸振器Zx相当于管道中一个不连续点，吸振器作为附加阻抗作用于管路上，在安装点使管路系统的阻抗发生了失配，因此在吸振器安装前后将会出现轴向弹性波透射与反射现象。

如图3所示，一轴向弹性波从管路左端入射过来，在吸振器位置处发生透射与反射，称之为弹性波散射现象。吸振器左端点轴向位移由入射波与反射波叠加，可以写成：

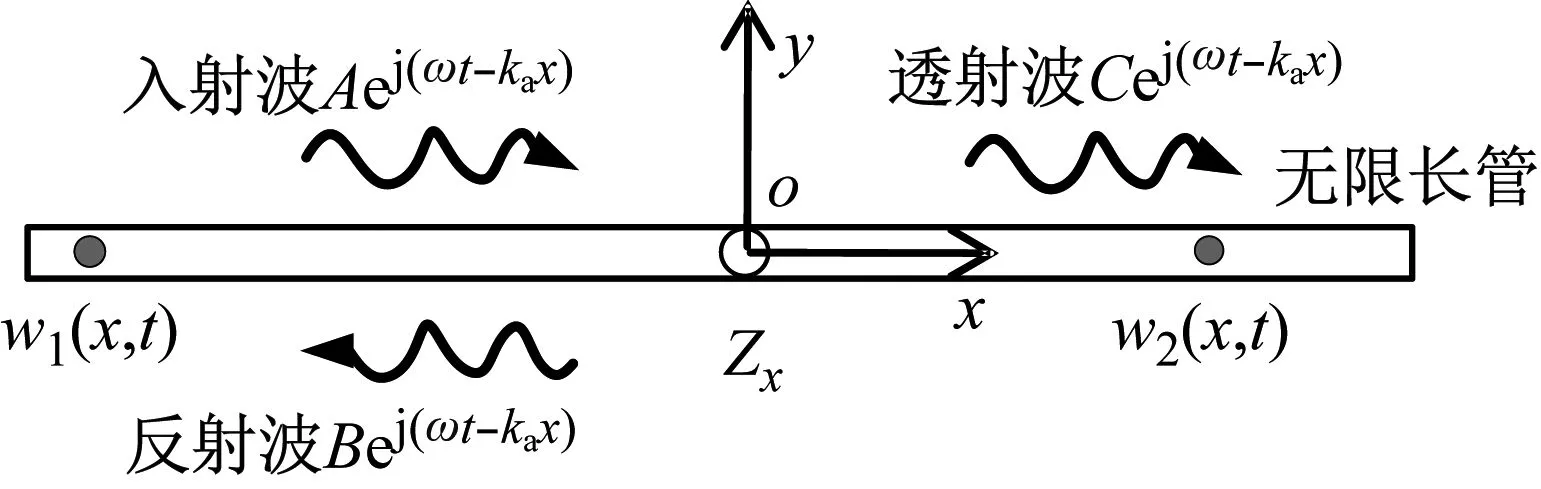
图3 无限长管轴向波传播示意图

w1(x,t)=Aej(ωt-kax)+Bej(ωt+kax)

(14)

右端点不考虑端部反射，轴向位移写成

w2(x,t)=Cej(ωt-kax)

(15)

式中：A、B、C为轴向波幅值；ω为圆频率；ka=ω/Cp为管道轴向波数；Cp为管道轴向波速。在坐标原点0处需要满足位移连续与轴向力平衡方程

w1(0,t)=w2(0,t)

(16)

式中，EAp为梁的轴向刚度。联立式(14)～(16)，可得管道轴向吸振器处反射与透射系数为

(17)

针对图1中的管路与轴向吸振器参数，将反射系数与透射系数对比如图4所示。

从图4中看出，在吸振器共振频率225 Hz处，沿管路轴向传播弹性波透射系数最小(≈0)，反射系数最大。由于弹性波在不连续点(吸振器)处需满足能量守恒，因此轴向波不是反射就是透射，当透射系数最小时，反射系数则最大，两者之和等于1。

从图5(a)中可以看出随着刚度的增加(K=1×106～1×109N/m)，反射系数的带宽变大，带宽起始与终止频率向高频移动。相反透射系数的带宽变窄。图5(b)中可以看出随着阻尼的增加(C=1～500 N·s/m)，反射系数的带宽变大，但主要集中在200～250 Hz范围内(图5(b)中的亮带内)，且随着频率的增加，反射系数的幅值逐渐减小，吸振器中阻尼越大，越有利于轴向波透射通过吸振器。

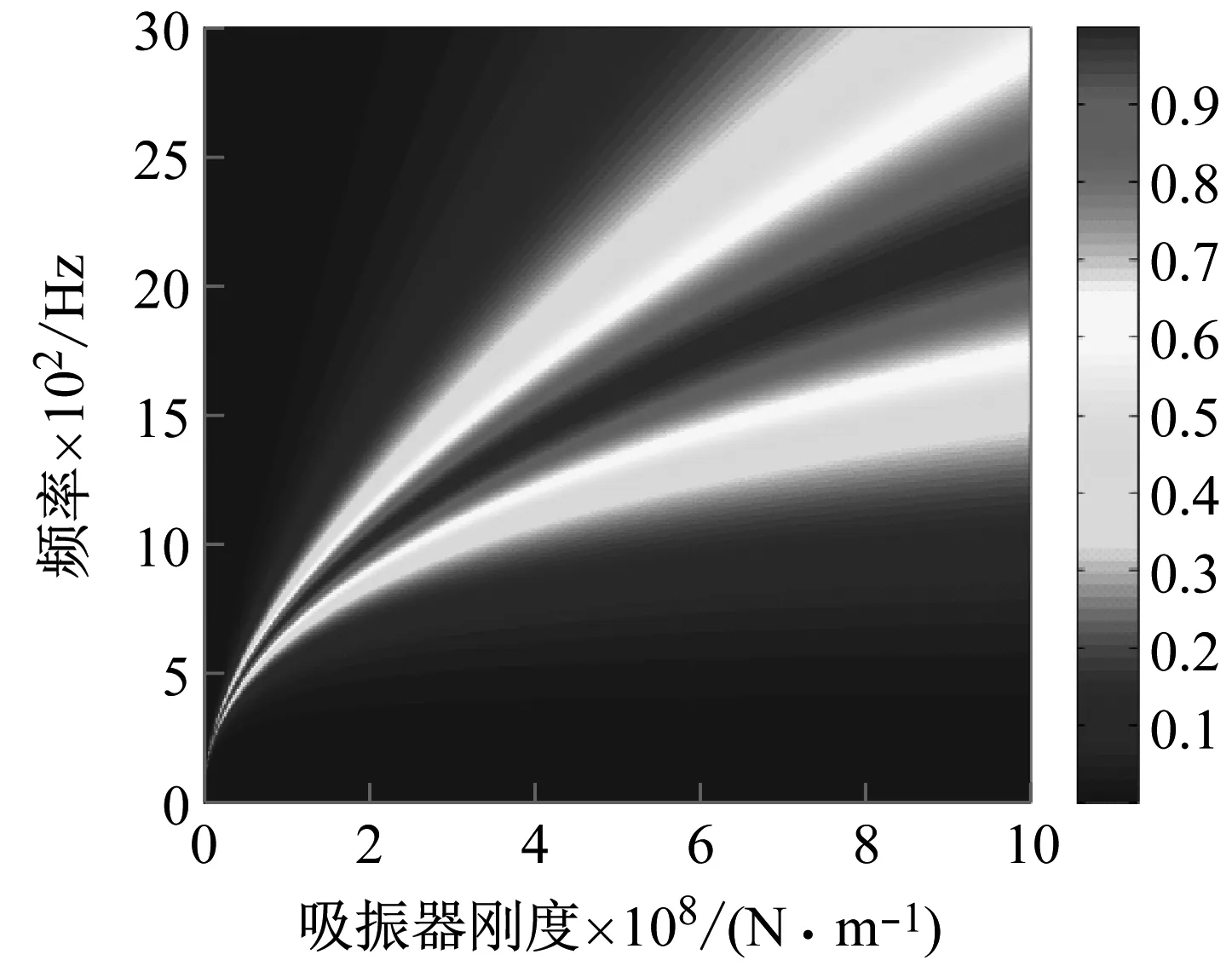
(a) 吸振器刚度刚度

3 带隙特性

当轴向吸振器沿管路轴向周期排列时，可以形成轴向局域共振型带隙(locally resonant，LR)，使得在某些特定的频率范围内，轴向振动波难以通过。

3.1 无限个吸振器带隙特性

常见的带隙求解方法有有限元法、级数展开法等，本文采用传递矩阵法。由文献[19]知带隙求解公式为

|T-ejκaI|=0

(18)

式中：κ为管路轴向波数向量，由实部、虚部两部分组成，实部为弹性波的传播项，虚部为弹性波的衰减项；T为周期吸振管路轴向传递矩阵，如式(13)所示；a为单个晶胞的长度，即吸振器之间的间距；I为4×4单位矩阵。通过求解式(18)的特征值，可以获得管路系统的带隙特性。

针对图1中几何参数不变，无限长管路-吸振系统，假设质量块保持不变，刚度从1×105～1×1010N/m变化，带隙随频率与刚度变化如图6所示。从图中可以看出，局域共振型带隙与Bragg带隙同时存在周期吸振结构中，随着吸振器刚度的增大，局域共振带隙的频带范围也相应增大，Bragg带隙则存在刚度较大且频率较高的范围内，且Bragg带隙的幅值远小于局域共振带隙。

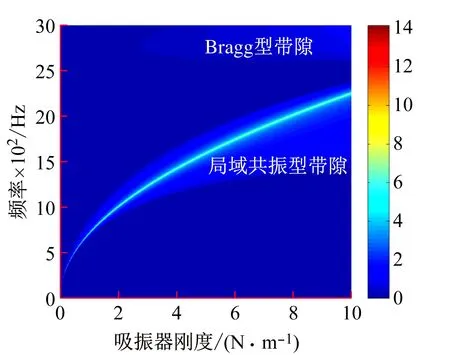
图6 刚度对带隙特性的影响

图7为不同吸振器刚度值下，无限长管路系统中轴向波矢虚部。当刚度小于1×106N/m时，吸振器阻抗与管路轴向阻抗相接近，无阻抗不连续点出现，因此不存在局域型共振型带隙；当刚度大于1×109N/m时，吸振器阻抗远大于管路阻抗，类似于给管路施加了一个刚性支撑边界条件，局域共振型带隙退化为Bragg带隙。

图7 不同吸振器刚度下波矢虚部

3.2 有限个吸振器带隙特性

3.1节研究了无限长直管上周期分布吸振器，而实际中吸振器安装个数与管路长度是有限的。如图8所示，管路规格、吸振器参数与图1中一致，长度为5 m，轴向周期均匀布置了5个吸振器，吸振器间距Δ=1 m。在管路右端施加一单位简谐力。

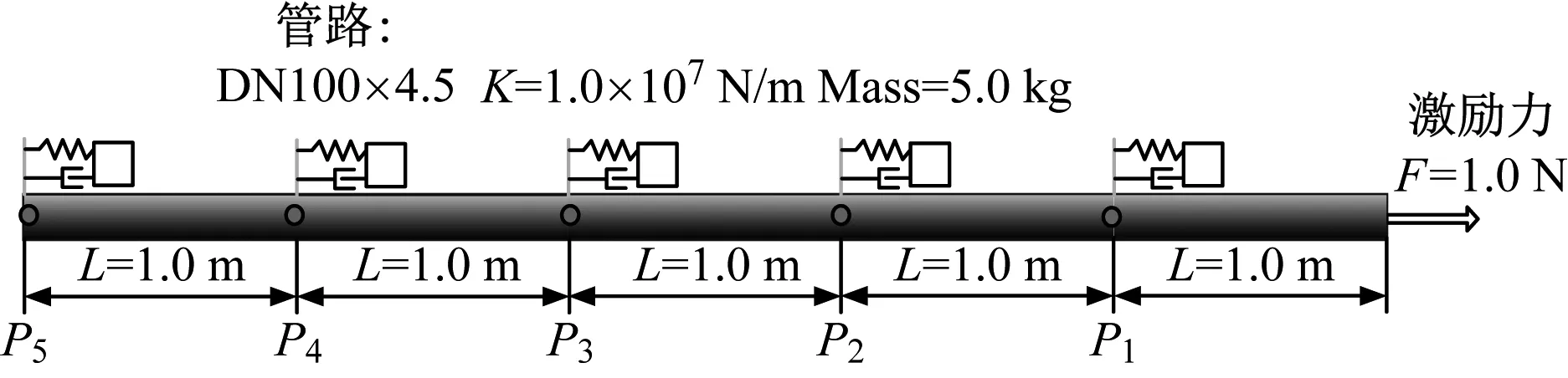
图8 管路轴向安装5个吸振器

五个吸振器安装位置为P1/P2/P3/P4/P5，由1.3节响应计算方法和3.1节带隙计算方法计算各吸振器安装点响应与带隙对比如图9所示。从图中可以明显看出674～884 Hz存在局域共振型带隙，管路中的轴向弹性波在该频率范围出现了“波停”现象，及轴向弹性波在该频率范围内无法进行传播，因此P1～P5点轴向位移大幅度的降低，且带隙频带范围宽度(674～883 Hz)远大于吸振器本身共振频率(712 Hz)。因此带隙虽能大幅度起到减振作用，但难以在低频段实现。

图9 带隙与位移响应

局域共振型带隙与Bragg带隙同时存在，由于Bragg带隙对应波矢实部(波矢实部控制衰减波)远小于LR带隙对应波矢实部，因此Bragg带隙对应的轴向弹性波减振效果并不明显。

4 结 论

采用传递矩阵法计算了一维管路轴向多吸振器的位移响应与轴向振动带隙，分析了轴向弹性波在吸振器前后的波动特性，并通过有限元仿真对计算方法进行了验证，主要结论如下：

(1) 可将吸振器作为管路附加阻抗，采用传递矩阵法能精确求解带多吸振器管路轴向振动位移响应；

(2) 轴向弹性波在吸振器共振频率存在明显的反射，刚度与阻尼的变化能有效的改变反射系数带宽；

(3) 多吸振器轴向管路中同时存在局域共振型带隙和Bragg带隙，且局域共振型带隙减振效果远大于Bragg带隙；

(4) 局域共振型带隙频带范围与位移响应结果一一对应，位移振动响应在带隙内得到了有效的控制，研究成果可为充液管路的减振设计提供参考。