四立柱可靠性试验载荷谱标准化方法研究

赵礼辉, 杨 鹏, 翁 硕， 冯金芝， 郑松林

(1. 上海理工大学 机械工程学院， 上海 200093; 2. 机械工业汽车底盘机械零部件强度与可靠性评价重点实验室， 上海 200093;3. 上海市新能源汽车可靠性评价公共技术服务平台， 上海 200093)

整车四立柱台架试验主要模拟道路的垂直冲击振动，用于研究整车的疲劳寿命，包括采集道路信号，编辑处理采集信号，识别系统频响函数，估计初始驱动信号，修正驱动信号和迭代以及执行道路模拟试验7个基本步骤[1]。由于在进行整车疲劳耐久试验前需要对每一个车型进行实测载荷测量，再按照试验场特定的路况迭代生成油缸作动器的信号，存在试验成本高和试验周期长等问题，难以在产品开发初级阶段进行快速有效地可靠性和耐久性验证[2]。

标准化载荷谱具有某一类典型结构实际使用或服役过程的共同载荷特征，具有普遍的代表性，可减少试验成本和试验周期[3]。自20世纪70年代开始，飞机工业最早开始研究标准化载荷谱。德国LBF和荷兰NLR研究所合作产生TWIST[4]，根据突风载荷的长度和强度分为十种类型，又把每种类型根据突风载荷的数量分为十种等级。标准谱于20世纪90年代在汽车工业的应用引起了广泛的关注，欧美汽车工业制定了关于轮轴结构的CARLOS[5]和CARLOS multi[6]。近年来又诞生了关于汽车传动装置的CARLOS PTA和和汽车拖车连接装置CARLOS TC。其中CARLOS multi是作用于汽车前轮悬架上的垂直、横向、制动和纵向四种方向的多轴标准化载荷谱。我国研究人员对标准化载荷谱也进行了相关研究。李珊珊通过载荷外推和威布尔分布拟合编制了海洋平台的T型管状接头的标准化载荷谱，该标准谱可用来计算裂纹尺寸，并减少数值模拟时间[7]。周楠基于航空发动机实测载荷计分析结果编制了冷端盘的标准化载荷谱。施闯闯通过关联损伤模型，结合同一试验场下不同车型载荷的雨流循环频次分布的相似性，建立了试验场的标准化载荷模型[8]。

但这些标准化载荷谱均是单轴载荷， CARLOS multi名义上是多轴载荷，其标准化方法仍然是将不同方向载荷单独考虑，未能考虑不同

载荷间的耦合效应。对于整车四立柱试验，不同车轮载荷存在明显相位关系，左右轮的非同步引起悬架的扭转，前后轮的非同步导致车身弯曲，而四个车轮载荷的非同步又使得车身发生扭曲。载荷间时域相位关系在整车上表现为不同的失效形式[9]，仅针对单轴标准化建立整车四立柱试验标准化载荷谱，最终不能准确反映汽车实际损伤情况。

因此，本文以整车四立柱试验为依托，提出一种综合四立柱载荷时域相关和频域相干特征的载荷谱标准化方法。以单一车轮功率谱密度为基础，生成随机载荷序列，基于频域相干关系和时域相关关系以及延迟关系，生成四立柱多轴载荷，并通过时域、频域、雨流、损伤等多维度进行有效性分析，最终通过实车四立柱试验进行验证，从而为整车可靠性与耐久性快速试验验证提供有效手段。

1 标准化方法

四立柱台架试验的输入信号包括油缸作动器的加速度、力和位移，由于不同车型轮心的力和加速度因悬架动态特性影响分布差异大，并且选用位移信号可以反应实车载荷，因此本文以四辆试验车四立柱台架试验的油缸作动器位移信号为基础数据建立整车四立柱台架试验标准化载荷谱，包括载荷特征分析、标准化载荷谱生成和标准化载荷效果分析三个部分。首先分析整车四立柱台架试验载荷，确定同一路况下不同车型垂向载荷分布的相似性。然后对不同车型同一车轮相同频率下的功率谱密度进行分布拟合并选择一定百分位的功率谱密度作为期望功率谱密度建立单轮驱动信号。其次为了复现左右两侧载荷之间时域上的相关性和频域上的相干性以及前后同侧载荷之间时域上的延迟，利用相干函数、相关系数和时延建立多轮驱动信号，并从多个方面分析标准化载荷谱，具体流程如图1所示。

图1 整车四立柱标准载荷谱编制流程图

2 整车四立柱载荷特征分析

2.1 时域及统计特征

本文以中等比利时路况为例分析载荷特征，车型1的四个车轮原始载荷历程如图2所示，该路况下四个车轮位移信号均为随机信号，时间历程最复杂，具有代表性。穿级计数表示统计载荷的上升边或下降边穿过某一级的次数，四个车型左前轮载荷穿级计数比结果如图3所示，分布具有相似性：频次随位移的增加而同步减小。幅值分布反应载荷落在不同幅值强度区域内的概率情况，四个车型左前轮载荷的幅值分布对比结果如图4所示，四个车型左前轮载荷幅值的最大值和最小值不同，但概率都呈现随幅值增大而减小的分布趋势。

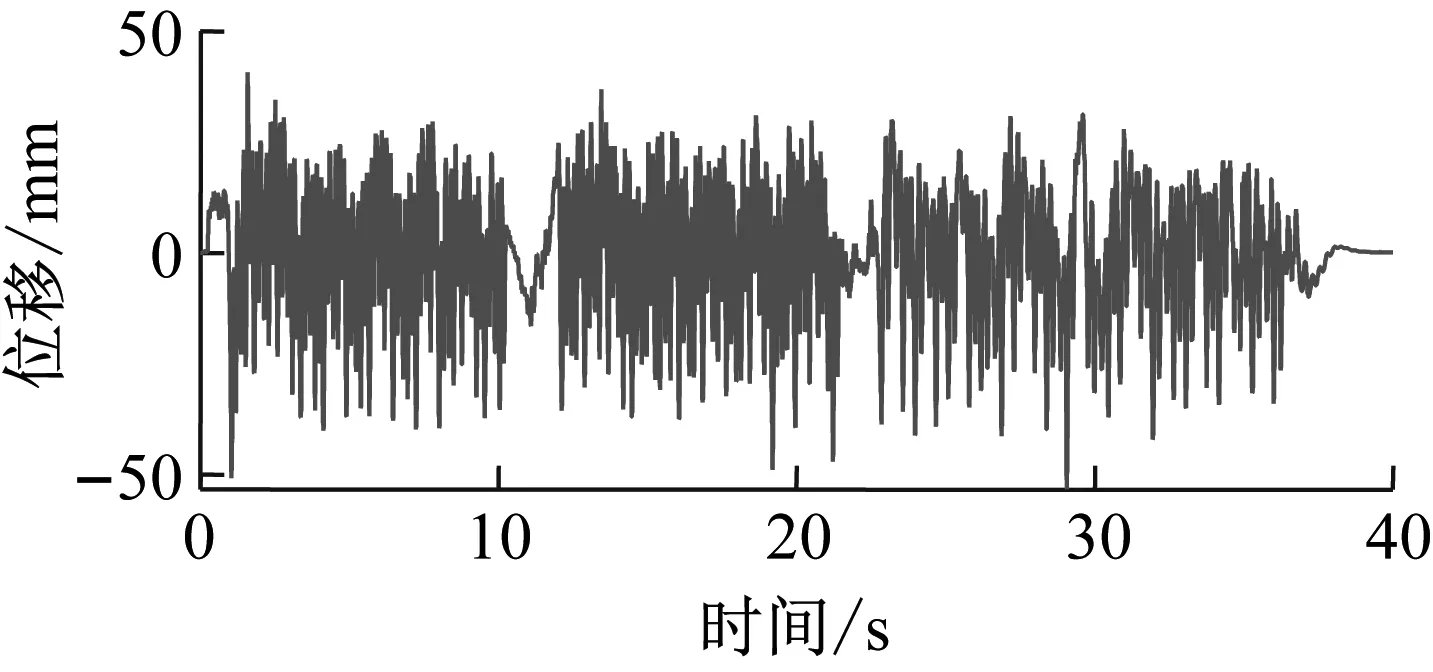
(a) 左前轮载荷时间历程

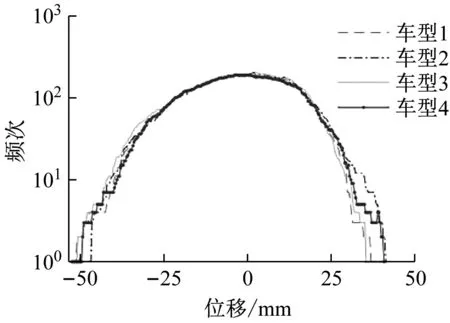
图3 穿级计数对比

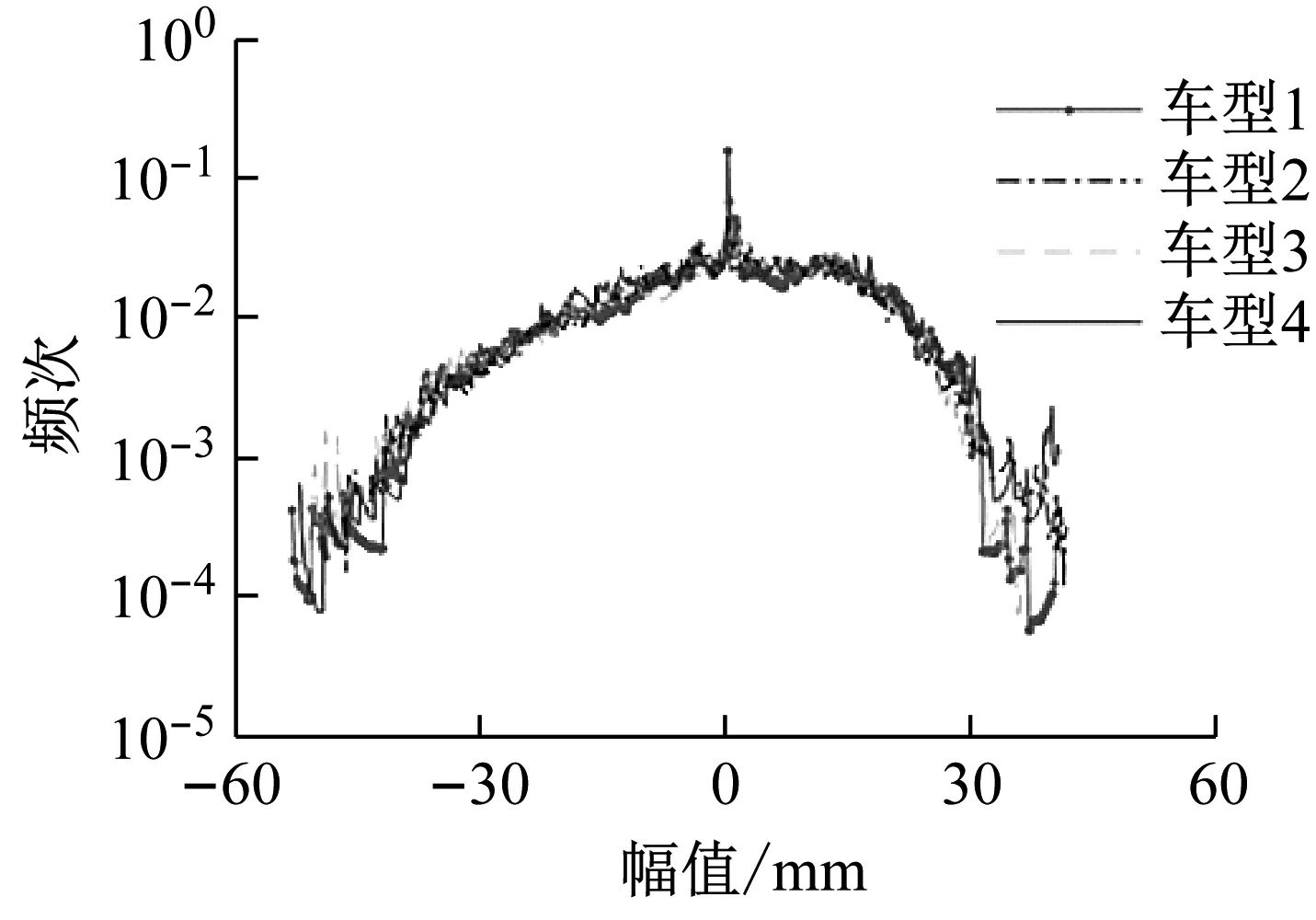
图4 幅值分布对比

时域统计特征对比如表1所示，四个车型左前轮载荷之间的最大值和最小值分布差异大；平均值分布差异小，都接近0；均方根表示信号的强度，车型1的均方根偏大，其余车型之间的均方根分布差异小；峰度表征信号的分布的阧缓程度，车型1的峰度偏大，其余车型之间的峰度基本一致。

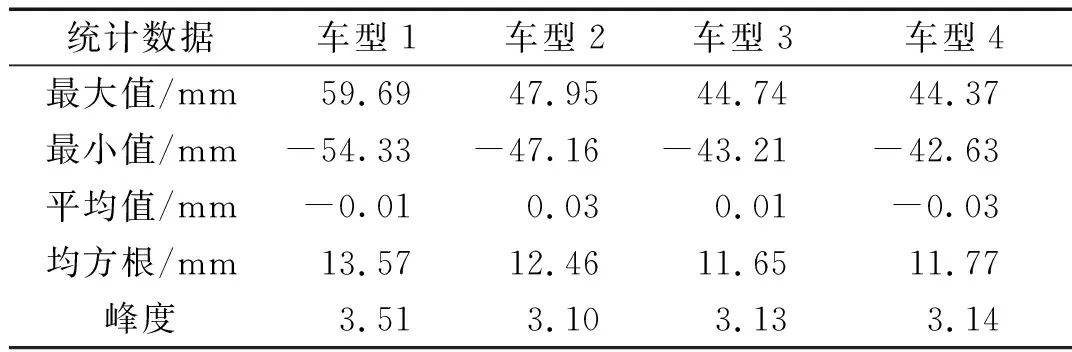
表1 原始谱左前轮统计特征

2.2 频域特征

功率谱密度简称PSD,表征单位频率上的能量分布，对比结果如图5所示，四个车型左前轮的能量主要集中在0～10 Hz频段上，峰值能量都在6.5 Hz处。冲击响应谱简称SRS，衡量结构在载荷下的动态响应，对比结果如图6所示，四个车型左前轮的SRS分布相似，载荷对结构产生最大的位移响应的都在6.5 Hz处。频域损伤谱简称FDS，衡量结构在激励载荷下不同频率下的损伤，对比结果如图7所示，四个车型左前轮的FDS分布相似，损伤主要都集中在0～8 Hz频段上，并且最大损伤都在6.5 Hz处。

图5 功率谱密度对比

图6 冲击响应谱对比

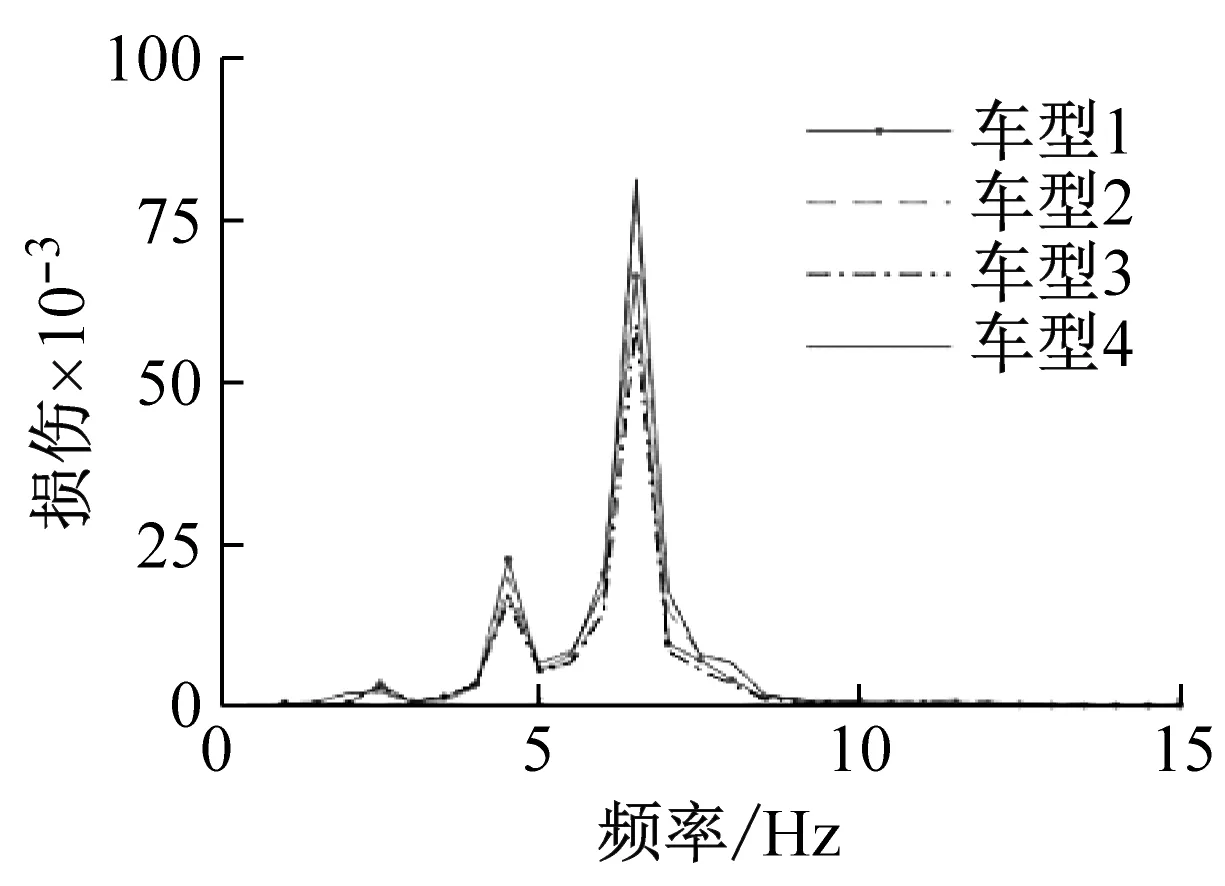
图7 频域损伤谱对比

2.3 雨流循环和损伤特征

雨流法是考虑材料应力-应变行为而提出的一种计数方法[10]。图8为四个车型左前轮的雨流计数对比结果，可以发现变程的最大值不同，但最大频次都出现在相同变程处，而且频次都呈现随变程的增加而下降的分布趋势。

图8 雨流循环计数对比

伪损伤是对载荷的强度进行量化评估的最常用的一种手段，它不需考虑具体结构[11-12]。本文结合S-N曲线和Miner线性累积损伤原则计算伪损伤，公式如下

⑴

式中:d表示伪损伤;Si表示幅值;β表示疲劳强度指数。

S-N曲线的截距和反斜率指数分别定为100和3。四个车型左前轮载荷的伪损伤分别为17.5、19.2、19.9和17.1，可以看出四个车型左前轮载荷的伪损伤分布差异小。

2.4 四轮载荷之间的耦合特征

汽车在实际行驶过程中，四个车轮载荷不是完全相互独立的信号。例如左、右前轮载荷之间具有时域上的相关性和频域上的相干性，左前轮载荷和左后轮载荷之间具有时域上的延迟性。相关系数用来描述两个信号之间相似程度，评价两个信号之间的相关性好不好[13]。相干系数则是频域的相关系数，用来描述两个过程在各频率上分量间的线性相关程度[14]。表2、表3、表4、表5分别为四个车型四轮载荷之间的相关系数，可以看出前后同侧载荷之间的相关系数小，左右两侧载荷之间的相关系数大。图9为四个车型左、右前轮载荷之间的相干系数，可以发现相干系数呈现在低频率带大和在高频率带小的分布趋势。

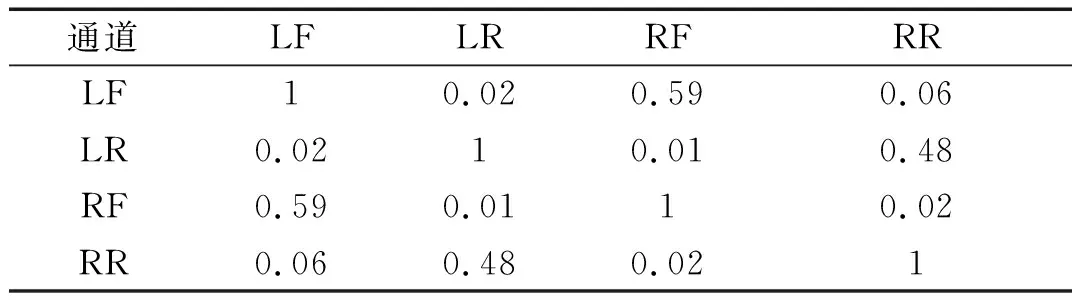
表2 车型1四轮载荷相关系数

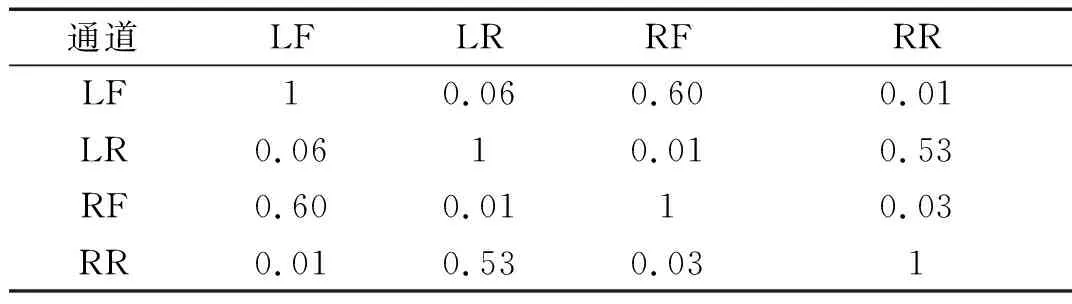
表3 车型2四轮载荷相关系数

表4 车型3四轮载荷相关系数

表5 车型4四轮载荷相关系数

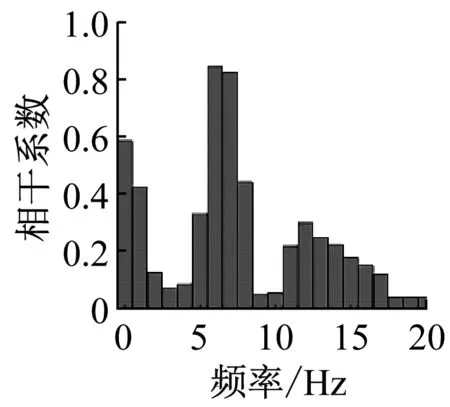
(a) 车型1

前后同侧载荷之间具有时间延迟，延迟时间t由整车轴距L和车速确定，即

⑵

前后同侧载荷延迟时间如表6所示，可以看出四个车型前后同侧载荷延迟时间分布差异小，都在0.3 s左右。将后侧载荷信号提前，消除前后载荷之间的延迟，再次计算相关系数，结果如表7所示，可以发现四个车型前后同侧载荷之间的相关系数提高到0.75以上，相关性大幅提高。

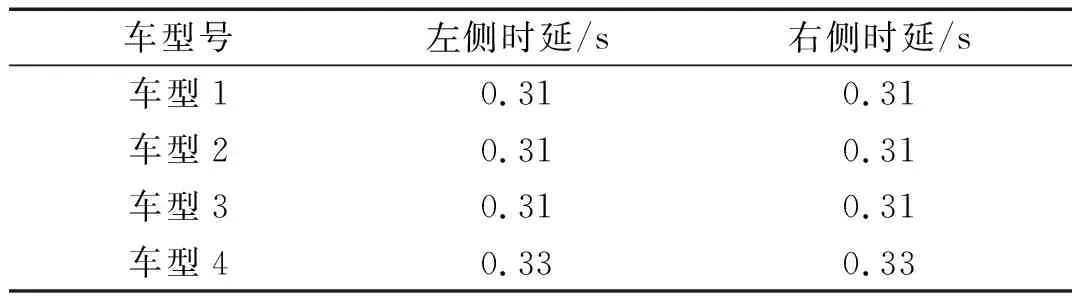
表6 前后同侧载荷延迟时间

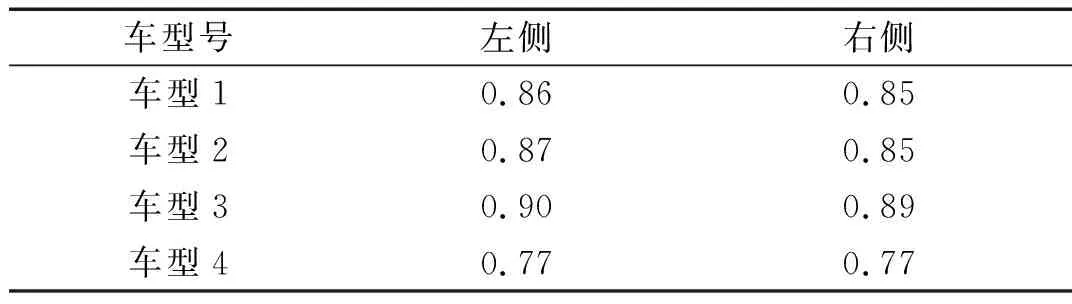
表7 修正时延后的前后同侧载荷相关系数

综合以上各种特征分析对比，可以发现在试验场同一路况可靠性规范下，不同车型同一车轮的垂向载荷分布具有相似性。

3 标准化载荷谱的生成

3.1 期望功率谱密度生成

首先要确定不同车型左前轮载荷在相同频率下的PSD接近哪种分布形态，然后选择一定百分位的PSD作为期望PSD用来涵盖四个车型的PSD。基于正态、威布尔和对数正态等各种分布模型，结合最小二乘法进行参数估计，最后通过Anderson-Darling(AD)检验确定最优分布函数[15]，AD检验统计量为

⑶

式中，Fn(x)为经验分布函数。

根据图4和图6，四个车型左前轮的能量和损伤都集中在0～8 Hz频段上，PSD最大值和FDS最大值都在6.5 Hz处，PSD的峰值分别分布在 0.5 Hz、4.5 Hz和6.5 Hz等处，因此以0.5 Hz和6.5 Hz处的PSD为例进行分布拟合，结果图10所示，可以看出不同车型左前轮在相同频率下的PSD服从正态分布，其次四个车型中左前轮相同频率下的最大PSD的累积概率接近90%，因此选择90百分位PSD作为期望PSD。

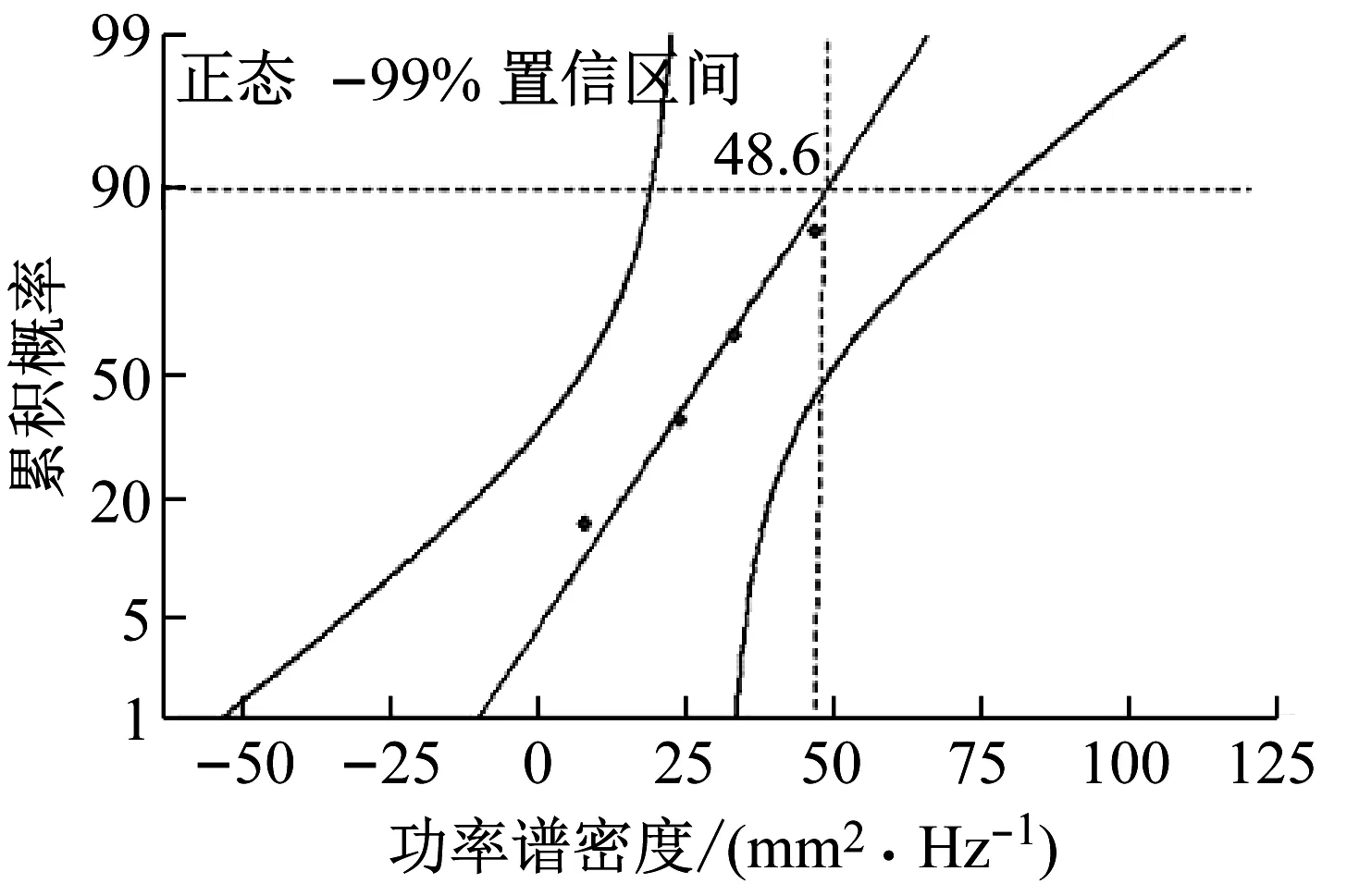
(a) 0.5 Hz处的PSD分布拟合

3.2 单轮驱动信号的生成

根据频谱幅值和功率谱的对应关系，可以求得与功率谱对应的一系列频谱幅值，在此基础上构造出相位谱生成频域信号，最后对频域信号傅里叶逆变换得到时域信号[16-17]，具体步骤如下：

(1) 计算频域信号的幅值。基于频谱幅值和功率谱的对应关系，得到频谱的幅值，即

⑷

式中：|Q(k)|(k=1,…,N/2+1)为频谱幅值；G(fk)为功率谱密度；N为数据点长度；Δt为时间分辨率。

(2) 构造频域信号的相位谱。对一组均匀分布的序列傅里叶变换得到在(0,2π)上均匀分布的相位谱φk。

(3) 计算剩余的频域信号。基于共轭关系，求出剩余的频域信号Q(k)(k=N/2+2,…,N)，即

⑸

(4) 计算时域信号。对频域信号傅里叶逆变换得到时域信号L(n)，即

⑹

3.3 基于相关系数的驱动信号生成

为了复现左、右前轮驱动信号之间在时域上的相关性，利用相关系数矩阵生成右前轮驱动信号LRF。

⑺

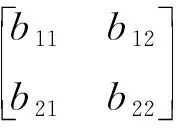
3.4 基于相干函数的驱动信号生成

基于相干函数和左前轮的频谱可得到右前轮的频谱，即

Q2(f)=Q1(f)coh(f)

⑻

式中：coh(f)为相干函数；Q1(f)和Q2(f)分别为左、右前轮的频谱。

再对右前轮频谱进行离散傅里叶逆变换即可得到右前轮驱动信号。

3.5 基于时延的驱动信号生成

根据上文修正原始谱前后同侧载荷的延迟，提高了前后同侧载荷之间的相关性，所以只需将标准谱前侧的驱动信号延迟即可得到标准谱后侧的驱动信号，即

⑼

(10)

式中：LLR和LRR分别为左、右后轮的驱动信号；l为轴距；v为车速。

因为相位谱为在(0，2π)均匀分布的随机变量，所以重构的载荷信号具有随机性，并且在时域上分布于零值上下。其次为了保证标准谱拥有更大的损伤强度，因此选用90百分位水平的功率谱重构单侧轮时域信号。

4 标准化载荷效果分析

4.1 时域和统计特征

基于相干函数得到的车型1标准化载荷时间历程如图11所示。为了分析标准化载荷的合理性，以左前轮为例进行各种载荷特征分析。表8为标准谱左前轮载荷的统计特征，可以发现标准谱的均方根偏大；标准谱的最大值、最小值、平均值和峰度接近原始谱。

(a) 左前轮载荷时间历程

表8 标准谱左前轮统计特征

图12为标准谱和原始谱的左前轮载荷幅值对比，可以看出标准谱和原始谱的左前轮载荷幅值分布相似。图13为标准谱和原始谱的左前轮穿级计数对比，可以看出分穿级计数分布相似，频次都随位移增加而同步减小。

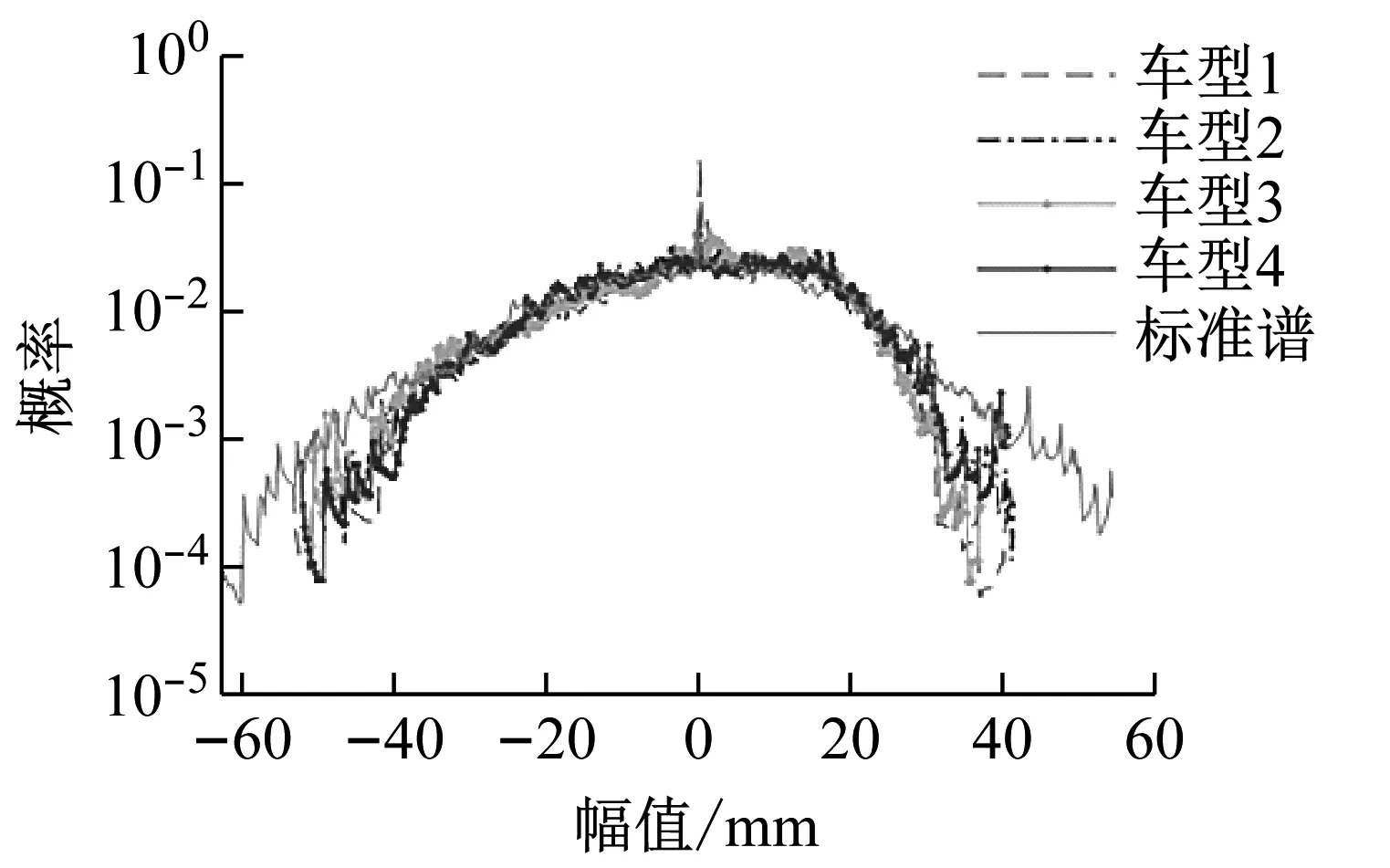
图12 标准谱和原始谱的左前轮幅值对比

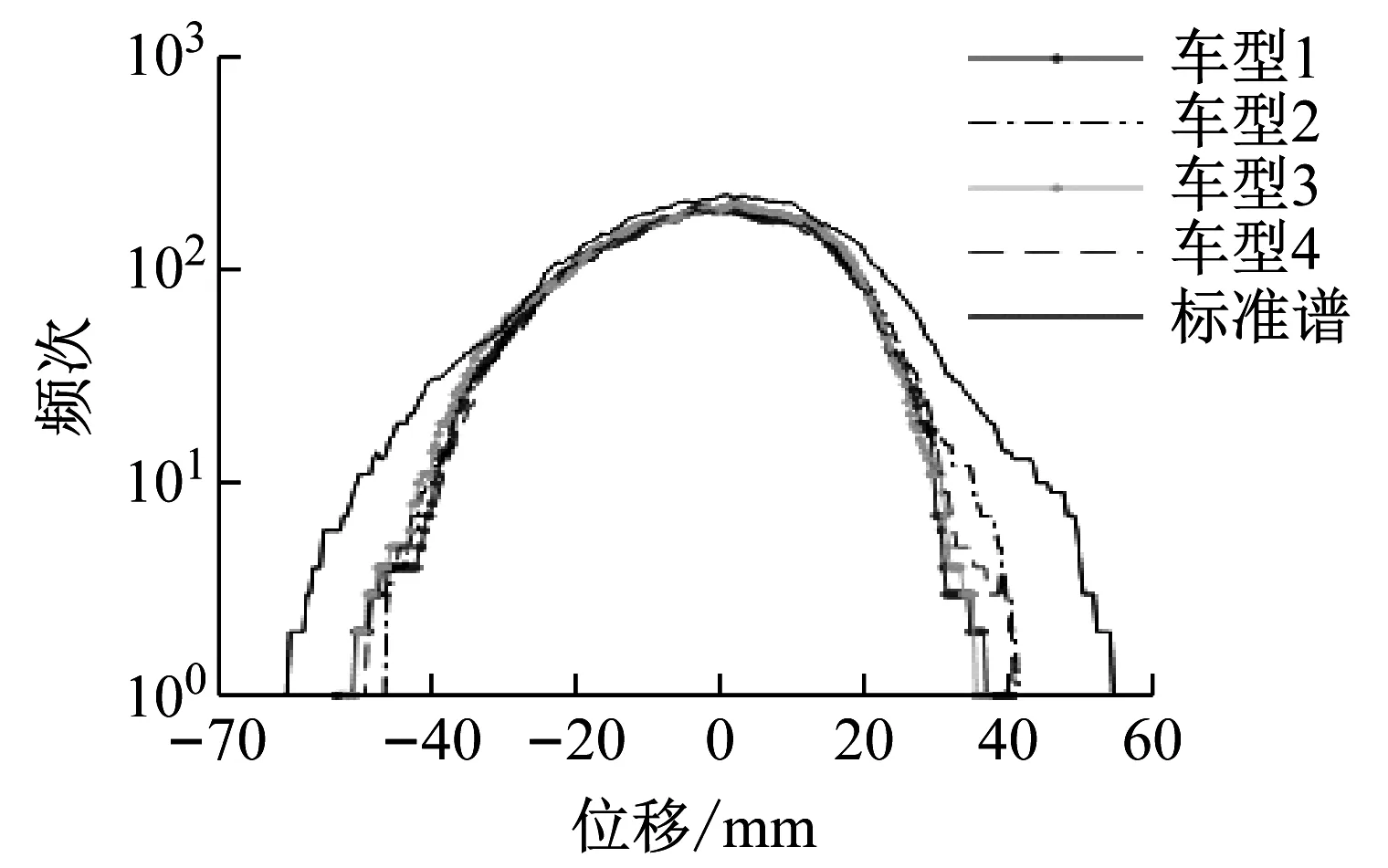
图13 标准谱和原始谱的左前轮穿级计数对比

4.2 频域特征

图14为原始谱和标准谱的左前轮SRS对比，可以看出标准谱和原始谱的左前轮SRS分布相似，冲击响应最大值都在6.5 Hz处。

图14 标准谱和原始谱的左前轮SRS对比

图15为原始谱和标准谱的左前轮FDS对比，可以看出标准谱和原始谱的左前轮FDS分布相似，损伤都主要集中0～8 Hz频带上，并且损伤最大值都在6.5 Hz处。

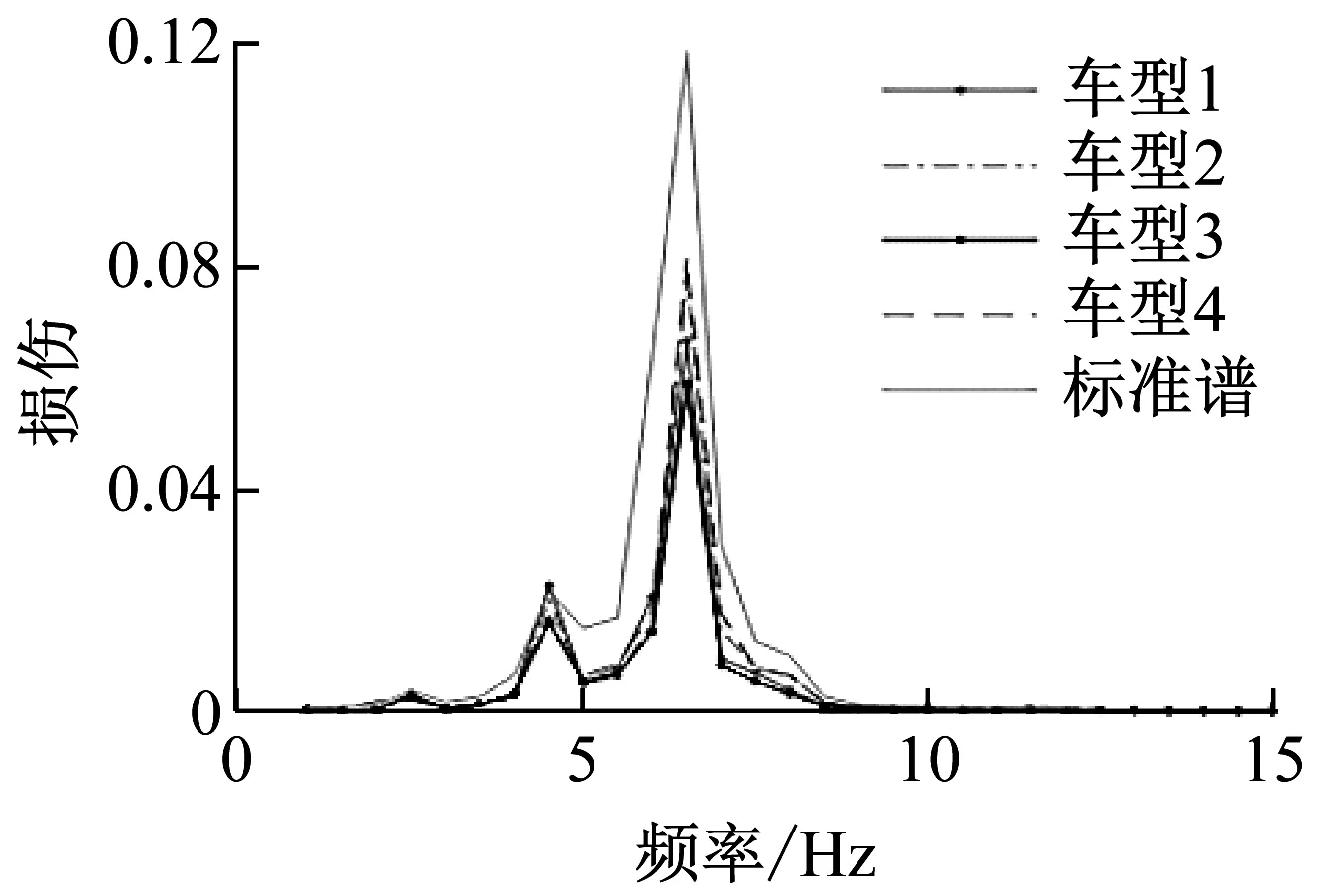
图15 标准谱和原始谱的左前轮FDS对比

4.3 相关性和相干性特征

基于相关系数得到右前轮时间信号，虽然复现了与左前轮时间信号之间的相关性特征，但是还需验证与左前轮时间信号之间的相干性特征是否复现。同理，基于相干函数得到的右前轮时间信号需要验证与左前轮时间信号之间相关性特征是否复现。

相关系数验证结果如表9所示，相干系数验证结果如图16和图17所示，可以发现基于相关系数得到的右前轮时间信号没有复现与左前轮时间信号之间的相干性特征，而基于相干函数得到的右前轮时间号复现了与左前轮时间信号之间的相干性特征和相关性特征。

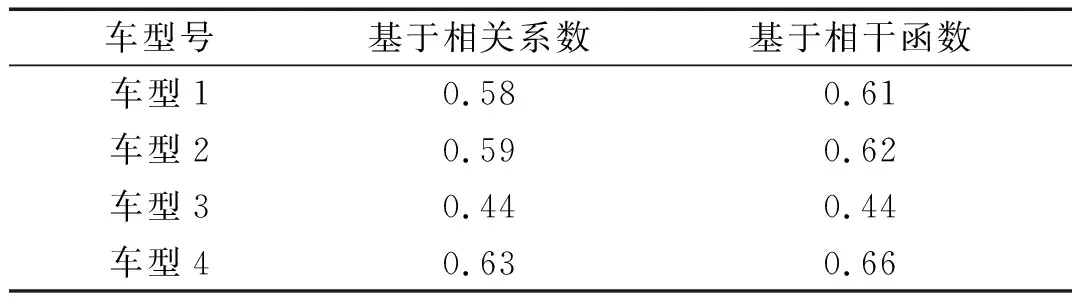
表9 相关系数检验

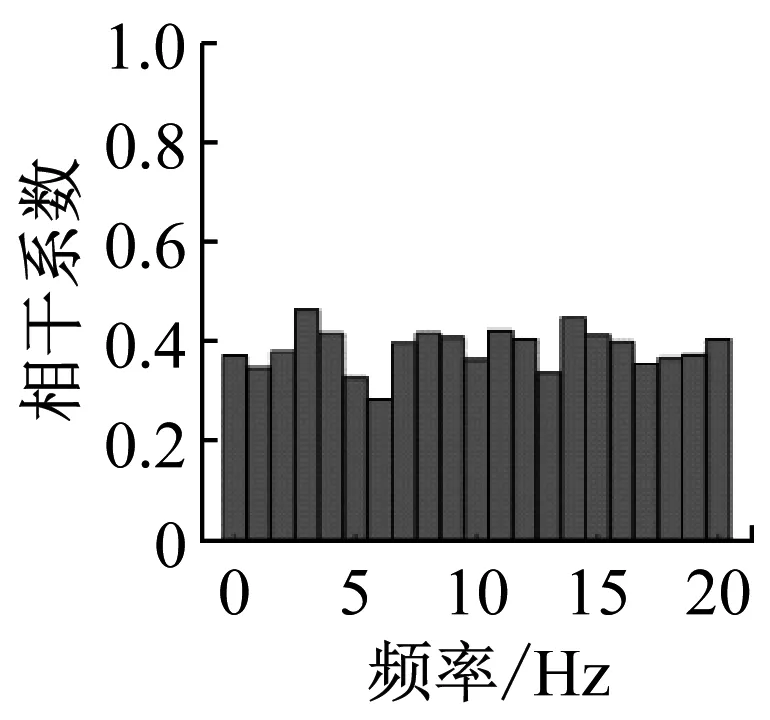
(a) 车型1

(a) 车型1

4.4 雨流循环和损伤特征

根据图18的雨流循环计数结果对比，可以看出标准谱和原始谱的左前轮雨流循环分布相似，最高频次都出现在相同变程处，并且频次呈现随变程增加而减小的分布趋势。

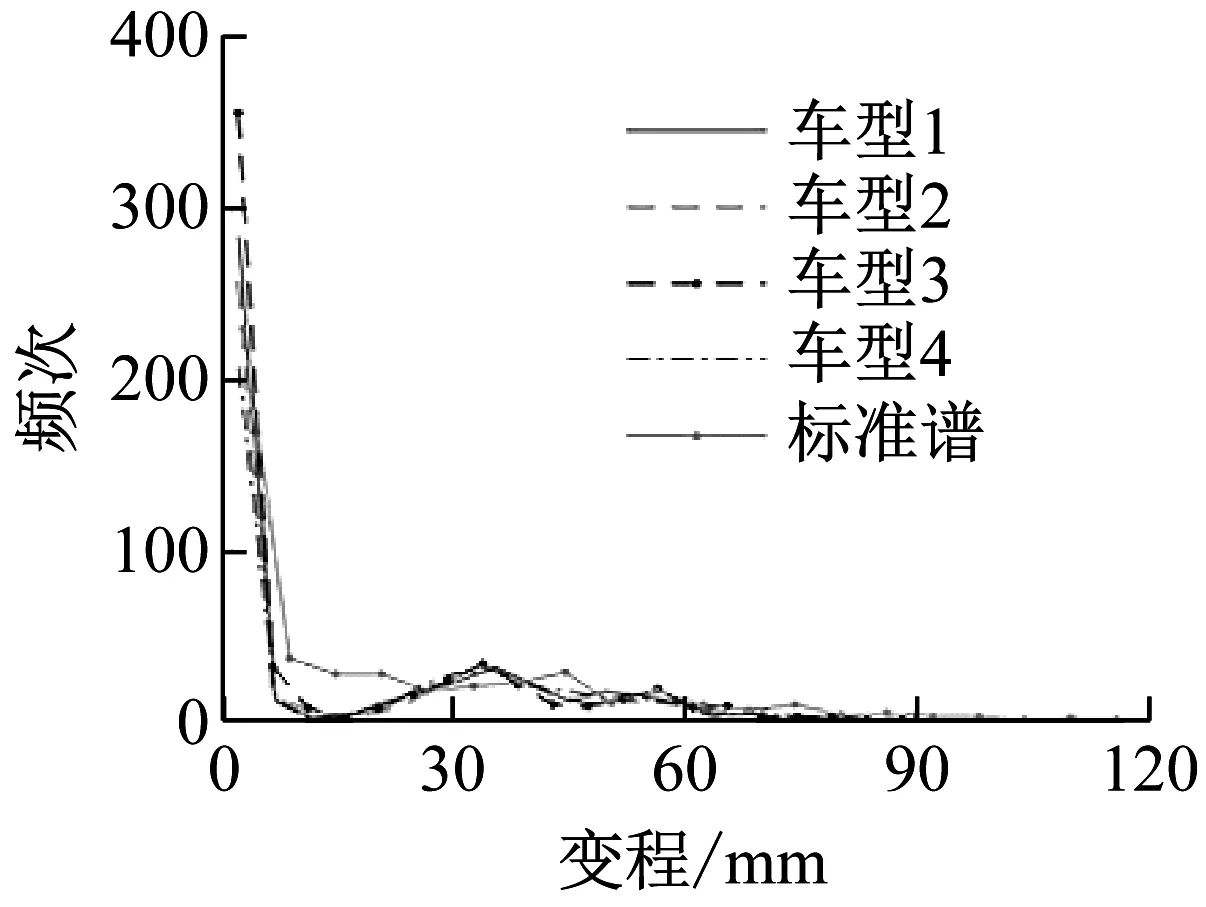
图18 标准谱和原始谱的左前轮雨流计数对比

基于相干函数得到的右前轮时间信号更合理，因此损伤效果只验证基于相干函数得到的时间信号。标准谱和原始谱的每个车轮相对损伤如表10所示，可以看出每个车轮的相对损伤均大于1，因此标准谱对每个车轮的损伤都得到了覆盖。

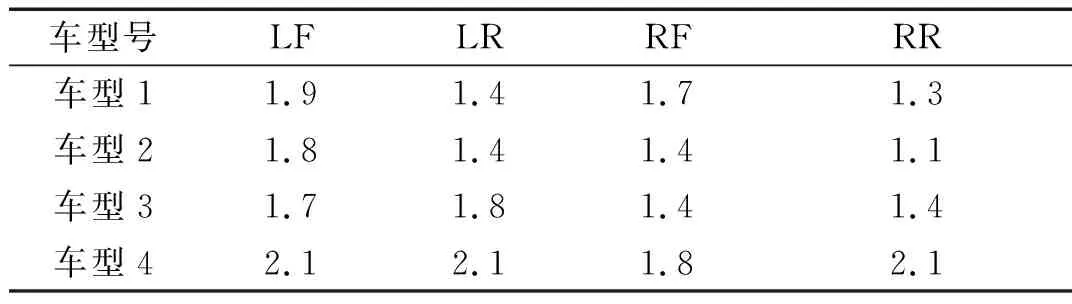
表10 每个车轮的相对损伤

汽车在行使过程中，四个车轮接触不同的路面，彼此之间的激励部分相关，四个车轮之间存在耦合效果，多轴耦合损伤表示为各个车轮载荷时间历程的线性组合下的一个新的载荷时间历程的伪损伤，汽车四个车轮载荷时间历程分别为S1(t),S2(t),S3(t)和S4(t)，因此线性组合下的载荷时间历程为[18]

S*(t)=αi*S1(t)+βi*S2(t)+γi*S3(t)+

φi*S4(t)

(11)

图19和图20分别为原始谱和标准谱的多轴耦合损伤结果，图21为标准谱和原始谱的每种组合相对损伤，可以看出每种组合相对损伤均在0.6～2.5，根据工程经验，当损伤比值的差值在2倍以内是符合近似相等的统计分布规律，即在限定范围内0.5～2，表明标准谱和实测谱具有近似相等的损伤能力，因此多轴耦合损伤也可较真实的再现。

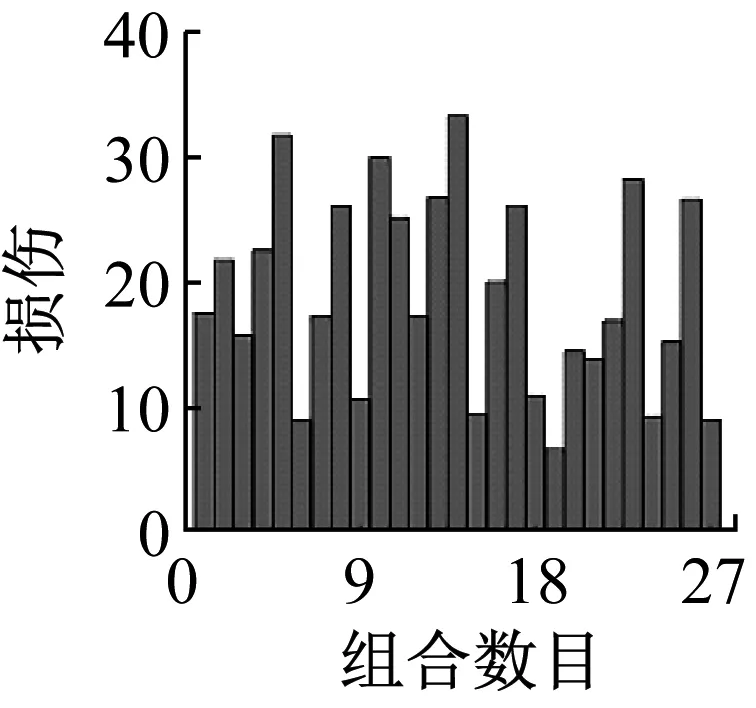
(a) 车型1

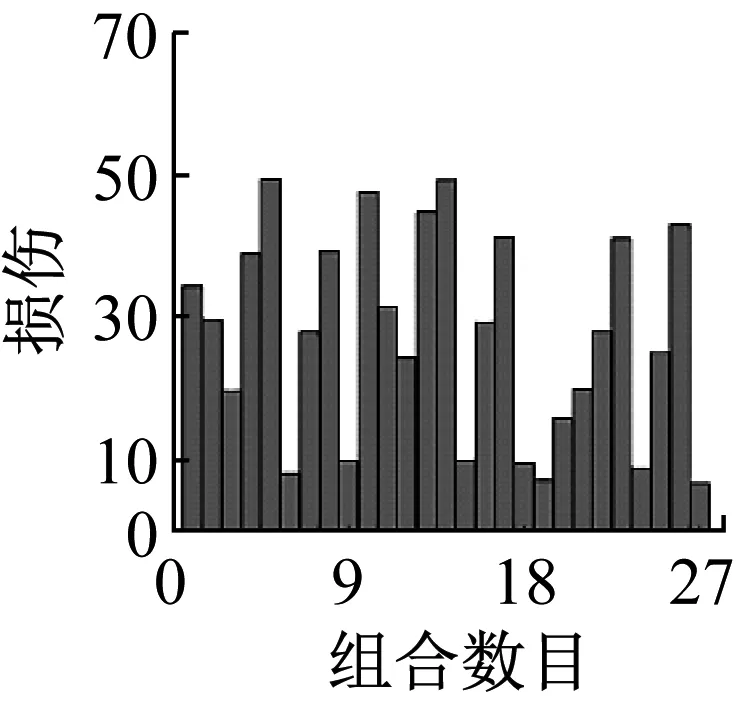
(a) 车型1

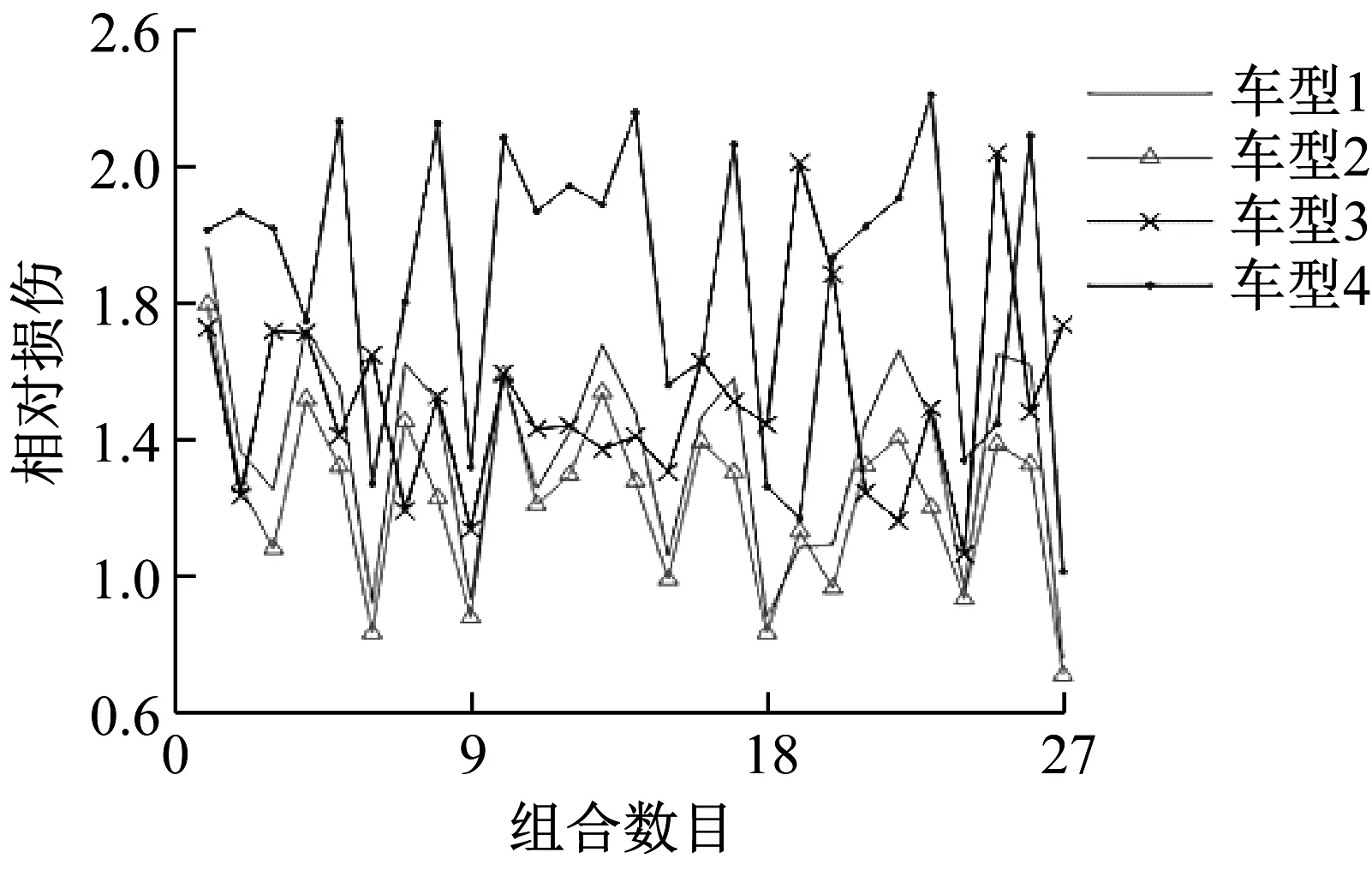
图21 标准谱和原始谱的每种组合相对损伤

4.5 室内道路模拟试验验证

为了验证标准化载荷谱的有效性，选取某SUV加载标准化载荷谱进行台架试验，试验过程中出现了与汽车试验场载荷下一致的失效模式，失效时间基本一致，失效位置都为汽车的右后轮罩，如图22所示。

(a) 原始谱

5 结 论

为了快速评估整车垂向载荷主导失效部件的可靠性与耐久性，本文基于整车四立柱台架试验实际载荷数据，开展了整车四立柱台架试验标准化载荷谱编制方法研究，主要结论包括：

(1) 针对四个轮心载荷间的相位和时延是整车弯曲和扭转疲劳的主要因素，提出了一种以四立柱位移PSD为源特征，左右两侧位移相关和相干为约束、前后同侧位移延迟为基础的载荷重构方法。

(2) 选择90百分位水平的功率谱重构的单侧轮时域载荷信号为基础建立的标准谱拥有更大的损伤强度，但台架试验组合工况结果存在风险，因此可以选择95百分位PSD甚至更高百分位的PSD生成标准谱进而保证多标准谱的多轴耦合损伤大于原始谱的多轴耦合损伤。

(3) 通过对比标准谱和实测道路谱之间的多种载荷特征，结果表明标准谱和实测道路谱的时域、频域和雨流分布基本一致；并且标准谱和实测道路谱的单轴损伤和多轴损伤分布也相同，单轴相对损伤比在1～2，多轴耦合损伤比在0.6～2.5，并以某SUV进行实际台架试验验证，出现了相同的失效模式和失效位置，表明了标准谱的合理性和有效性。