基于改进T-B谱方法的高层建筑风致疲劳损伤分析

黄国庆， 范宇航， 姜 言

(1. 重庆大学 土木工程学院， 重庆 400045; 2. 西南大学 工程技术学院， 重庆 400715)

随着钢材等轻质高强材料的广泛使用，使得高层建筑朝着高耸、轻柔的方向快速发展。由于结构刚度和阻尼的不断减小，结构风敏感性的逐渐增加，抗风性能已成为结构设计的控制性因素[1]。一方面，风荷载作用下的过大变形或振动，严重影响了结构的安全性和舒适性。另一方面，当风荷载长期、往复地作用在结构上时，尽管循环应力远小于材料极限应力，但结构内部会产生疲劳损伤，待损伤累积到一定程度，结构会发生疲劳破坏。不同于强度破坏，疲劳破坏是一种长期效应，具有强隐蔽性[2]。因此，评估高层建筑的疲劳损伤对其耐久性研究至关重要。

目前，结构疲劳损伤分析方法主要有时域法和频域法。其中，时域法需获得结构关键位置处的应力时程，之后通过循环计数方法得到该应力时程的应力幅值分布、平均应力以及循环次数等，最后结合疲劳损伤理论和材料S-N曲线来进行疲劳损伤估计[3]。常用的时域法为雨流法[4]。该方法精度高且应用范围广，故常被作为评价其他方法准确性的基准[5]。然而随着应力时程的不断增加，该方法计算效率逐渐降低。

不同于时域法，频域法是根据荷载作用下结构关键位置处应力时程的统计特性来描述应力幅值以及循环次数等信息，并结合疲劳损伤理论和材料S-N曲线估计疲劳累积损伤。该方法能够避免繁琐的时程分析，因而具有良好的工程应用前景。常用的频域法有窄带法[6]、等效窄带法[7]、等效应力法[8]、Dirlik疲劳计算公式[9]、Zhao-Baker疲劳损伤公式[10]和Tovo-Benasciutti谱方法(T-B谱方法)等[11]。其中，T-B谱方法具有广泛的适用范围和较好的理论基础。该方法不仅形式简便，而且可以给出明确的循环分布信息，甚至可以应对非高斯应力响应过程所引起的疲劳损伤问题[12]。

然而随着反映材料疲劳特性曲线(S-N曲线)的斜率参数增加，T-B谱方法与雨流法的差异逐渐增加。鉴于此，本文首先以高层建筑顺风向、横风向以及耦合风振疲劳损伤为研究对象，并以时域雨流法为基准，评价了原有两种T-B谱方法的计算精度；其次，基于该方法关键参数的分析结果，并利用数值模拟，给出了关键参数的包络值；最后，基于该包络值提出了改进的T-B谱方法，同时验证了其有效性。

1 高斯随机过程下疲劳损伤的分析方法

1.1 时域法

时域内计算疲劳损伤最直接的手段就是利用循环计数法统计出应力幅值分布、平均应力以及循环次数等关键信息，再结合材料S-N曲线和疲劳损伤理论来估计疲劳损伤[13]。目前，常用的循环计数法主要包括峰值计数法、界限计数法、幅值平均计数法以及雨流计数法等。其中，Matsuishi和Endo提出的雨流计数法具有最好计算精度。该方法能较好地反映随机加载的全过程，其特点是识别响应时程曲线的每个回转点，并记下完整的滞回环，进而得到一个振幅为行、均值为列的矩阵。分析每个均值和振幅，可得对应的滞回环数目，从而获得各应力幅下结构的实际循环次数[13]。

材料S-N曲线表示了应力幅与循环次数之间关系。常用的S-N曲线为幂函数形式[14]

N(p)=Cp-m

(1)

式中：N(p)为常幅疲劳荷载p下，材料达到疲劳破坏的循环次数；m为斜率参数；C为参考疲劳强度。

基于材料的S-N曲线，结合Miner线性累积损伤法则[15]，则累积疲劳损伤可表示为

(2)

式中：D为累积损伤值(D≤1)，D=1表明结构处于疲劳破坏临界状态；nu为应力幅pu所对应的循环次数；Nu为常幅疲劳荷载pu作用下，材料疲劳破坏的循环次数，可由式(1)获得；n为总的循环次数。

通过实测或者数值模拟得到疲劳破坏控制点的应力时程后，利用雨流计数法可得相应的应力循环幅值等信息。如果不考虑平均应力的影响，可得该时程内的累积疲劳损伤为

(3)

1.2 频域法

对于零均值的窄带随机过程X(t)，其响应应力幅值p的概率密度函数服从瑞利分布，即[16]

(4)

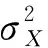
(5)

(6)

式中:0≤α1≤α2≤1，当α1=α2=0时表示相应的响应过程为白噪声，而当α1=α2=1时响应过程为严格的窄带随机过程；λv为功率谱SX(f)的v阶统计矩。

结合疲劳Miner线性损伤理论和材料的S-N曲线，可得窄带高斯过程的疲劳损伤率为

(7)

相比而言，宽带高斯过程的应力幅分布形式复杂，目前尚无理论结果。为了准确地评估宽带高斯过程的疲劳损伤，许多学者提出了一系列经验公式来近似表达该过程下的应力幅分布，如T-B谱方法等。通常，利用线性损伤准则估算宽带高斯随机过程的疲劳损伤存在以下关系

E[DRM]≤E[DRF]≤E[DLC]=E[DNB]

(8)

式中:E[DRM]、E[DRF]和E[DLC]分别为幅值平均法、雨流法和界限法估计的疲劳损伤率；T-B谱方法将雨流法结果近似表示为E[DRM]和E[DLC]的线性组合，即：

E[DRF]≈E[DTB]=bE[DLC]+(1-b)E[DRM]=

(9)

式中，b为待定系数，其反映了上述三种方法之间的关系。明显地，如何确定参数b是利用该方法的关键。其现有结果主要为数值模拟得到的拟合解，包括Tovo和Benasciutti提出的拟合结果

(α1+α2))e2.11α2]

(10)

以及Ding和Chen根据高层建筑风致结构疲劳响应获得的拟合解等

(11)

2 高层建筑风致疲劳损伤分析

本节以高层建筑顺风向、横风向以及耦合风振响应(结构基底应力响应)产生的疲劳损伤为例。其中，耦合响应为顺风向响应和横风向响应的矢量和，且仅考虑一阶线性模态作用。该结构位于城市当中，高度H为200 m，宽度B和深度D均为0.2H，且假定质量沿高度均匀分布；结构顶端平均风速的取值范围为5～50 m/s，间隔为5 m/s；结构顺风向和横风向基频分别为0.230 Hz和0.276 Hz；结构材料为Q345钢材，材料弹性模量为206 GPa、泊松比为0.3；材料S-N曲线参数m的取值为3～5[17]，C的取值1.28×1011(MPa)3[18]，且不随m变化；结构的阻尼比分别取0.01、0.02和0.05，未考虑瑞利阻尼。

需要说明的是，钢材S-N曲线可能存在一条水平渐近线，即材料疲劳极限强度。当构件荷载小于疲劳极限时，理论上该构件不会产生疲劳破坏。由于高层建筑在设计服役期内的循环次数远大于疲劳极限循环次数，为计算方便，往往不考虑材料疲劳极限，且认为所有应力循环都会产生疲劳损伤。显然，上述假设是偏安全的。

2.1 荷载响应谱及其特性

由于仅考虑一阶线性模态下的响应，该结构广义荷载Q(t)可通过其基底弯矩M(t)计算获得，即Q(t)=M(t)/H。本研究采用了日本建筑学会所(AIJ)提出的方法[19]，通过归一化的基底弯矩即基底弯矩系数来计算结构响应谱，具体过程如下：

对于顺风向响应来说，其基底弯矩系数功率谱可表示为

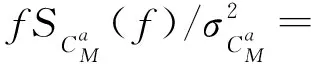
(12)

其中，

(13)

(14)

(15)

对于横风向响应来说，基底弯矩系数功率谱可表示为

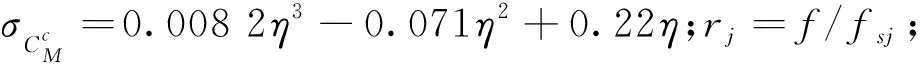
(16)

(17)

β2=0.28η-0.34

(18)

(19)

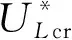
(20)

式中:ζ为结构阻尼比；M为结构总质量。

就本文所述结构而言，当阻尼比ζ为0.01时，结构顶端风速(最大为50 m/s)满足不等式(16)的约束。结合式(17)，可知当阻尼比为0.02和0.05时，临界风速取值更大，因此本文所述结构无需验算涡激共振。

根据上述基底弯矩系数谱，可得广义力荷载谱，进而结合结构频响函数获得位移响应谱。将位移响应乘以常数系数M1(2πf1)2Hφs(M1为广义质量；φs为单位弯矩下的基底应力)，可得最终的应力响应。由于仅考虑一阶线性模态下的响应，则结构顶端位移响应特性与基底应力响应特性一致。图1～3分别给出顺风向、横风向以及耦合风振作用下相应的疲劳响应带宽参数结果。

图1 顺风向响应带宽参数

图2 横风向响应带宽参数

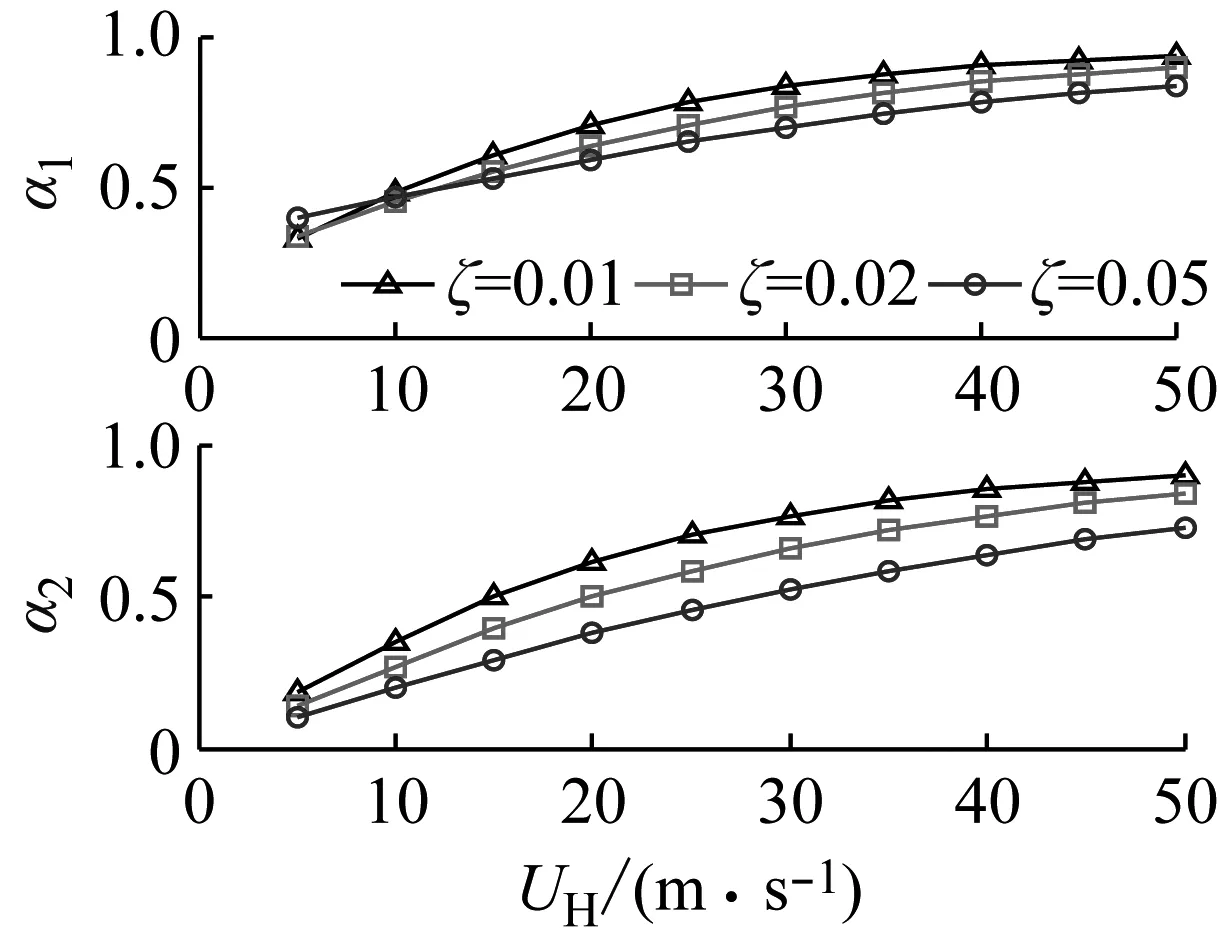
图3 耦合响应带宽参数

由图1～3可知，带宽参数随风速增加逐渐增大趋近于1，阻尼比的减少又会加剧上述变量的变化程度。换而言之，随着风速的增加和阻尼比的减少，响应过程越来越趋近于窄带随机过程。其中，顺风向响应具有最宽的带宽参数。

2.2 改进的T-B谱方法

基于上述荷载响应谱，本节以时域雨流法为基准来评估T-B谱方法的性能。首先，利用经典谱表示法模拟广义力谱所对应的广义力时程(以风速为20 m/s、阻尼比取0.01为例，给出了顺风向结果，如图4所示)，采样频率为10 Hz，模拟时距为8 000 s；采用8 000 s时距的原因见附录；其次，将广义力荷载加载在结构上，通过Newmark法计算得到应力响应时程(即名义应力时程)；最后，利用雨流法估计该段时程所产生的平均疲劳损伤DRF。上述过程进行1 000次，取平均值并记为E[DRF]。

图4 顺风向广义力时程图

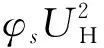
图5 应力循坏次数和应力幅的统计结果

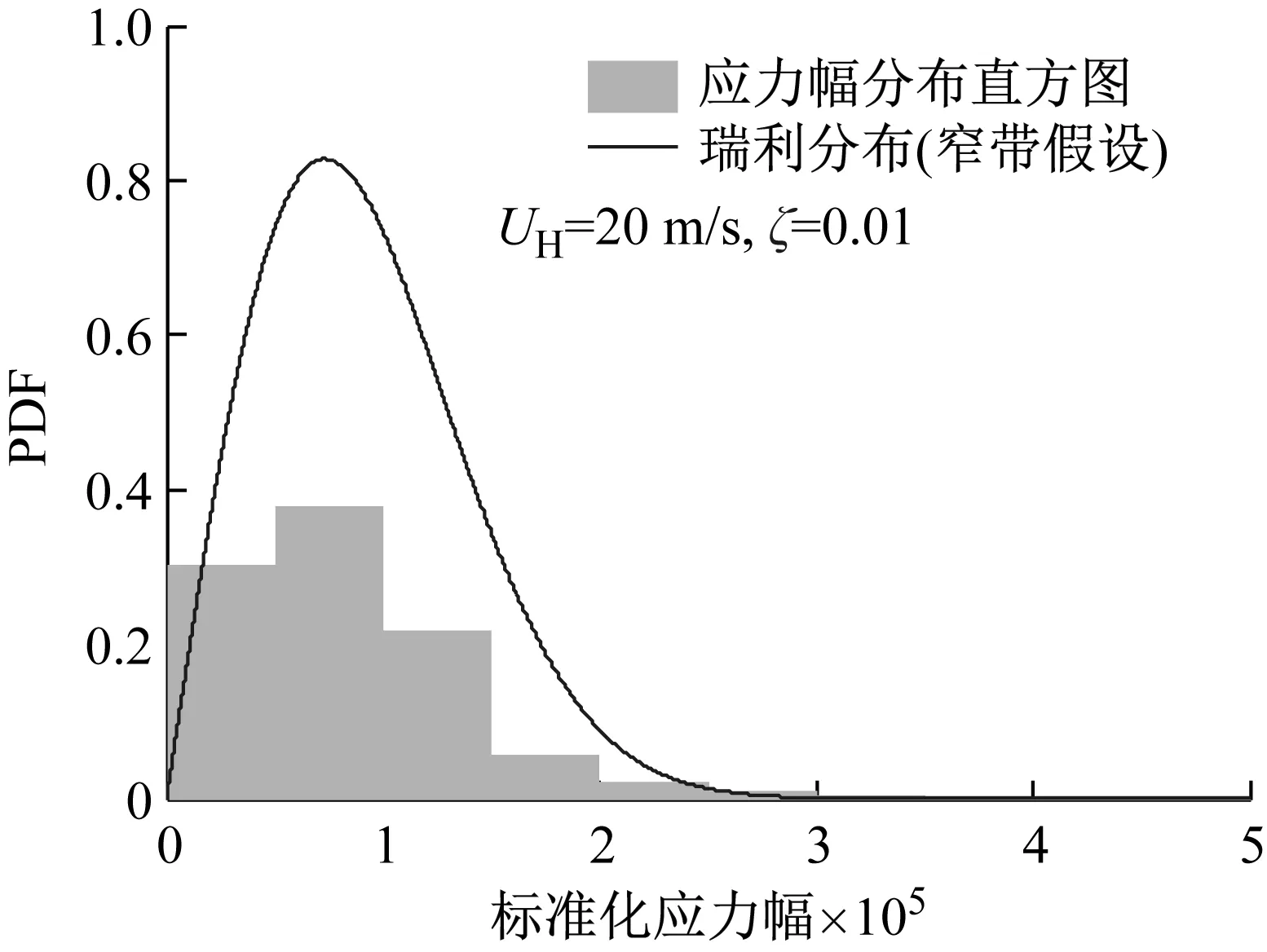
图6 应力幅分布

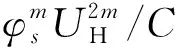
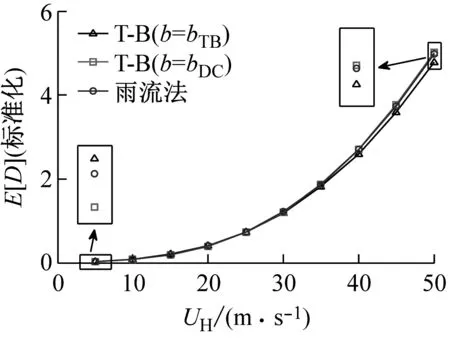
(a) 顺风向

为了进一步评估T-B谱方法的计算精度，图8以阻尼比取0.01为例，给出了m取值分别为3、4和5时，雨流法和T-B谱方法计算结果间的误差结果。该误差被定义为

(21)

由图8可知，随着m的增加，雨流法和T-B谱方法间的误差越来越明显，甚至超过了20%。其中，对于带宽较宽的高斯随机过程来说(即风速较小处)，采用b=bTB计算方法具有较好的预测精度；而对于带宽较窄的高斯随机过程来说(即风速较大处)，采用b=bDC估计方法具有更高的精度。因此，需要对参数b展开进一步研究，来更好地估计疲劳损伤。

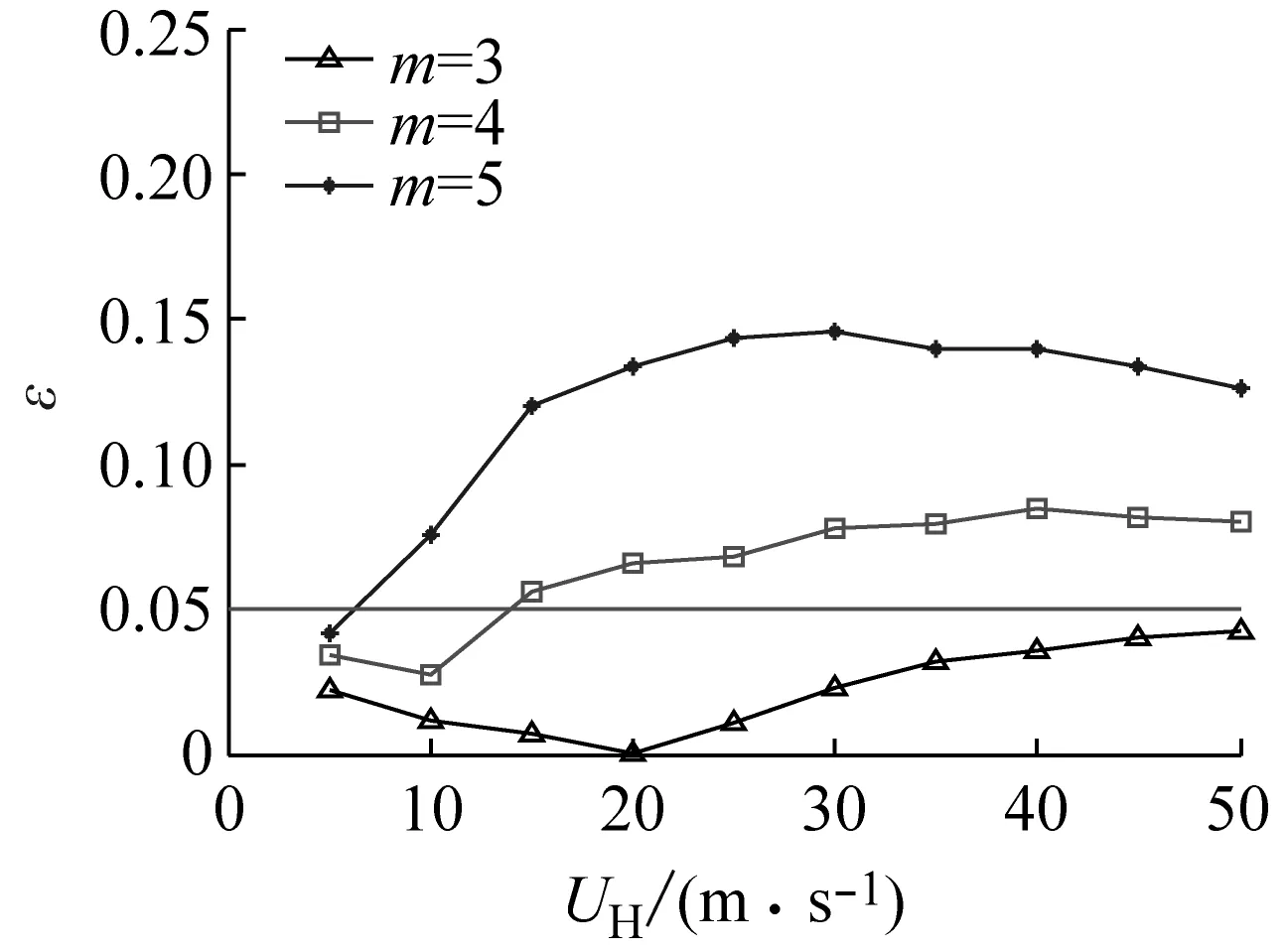
(a) bTB顺风向

图9给出了三种b值的结果，即雨流法确定的bsim和基于T-B谱方法的两种拟合值(分别为bTB和bDC)。由图9可知，bsim与bTB和bDC之间的最大值较为接近。基于此，给出了参数b的新拟合结果

(a) 顺风向

bsim≈bnew=max(bTB,bDC)

(22)

表1～3分别给出了m取3、4、5的情况下，原有T-B谱方法及改进方法分别与雨流法之间的误差。由表可知，改进方法的精度相较原有方法均有一定程度的提高且最大误差不超过20%。其中在m为3时，改进方法与雨流法间的误差均小于2.5%(最大误差为2.48%)。以横风向结果为例，其平均误差仅为0.96%，而原有T-B谱方法的平均误差分别为4.25%和2.14%。为了进一步分析，表4给出了阻尼比为0.01时，改进方法的平均误差相对原有T-B谱方法的降低程度，以横风向结果为例，m为3时其降低程度分别为77.49%和55.38%；m为4时其降低程度分别为53.89%和16.72%；m为5时其降低程度分别为46.36%和14.98%。此外，当阻尼比为0.02和0.05时，所得结果与上述类似，故不再赘述。

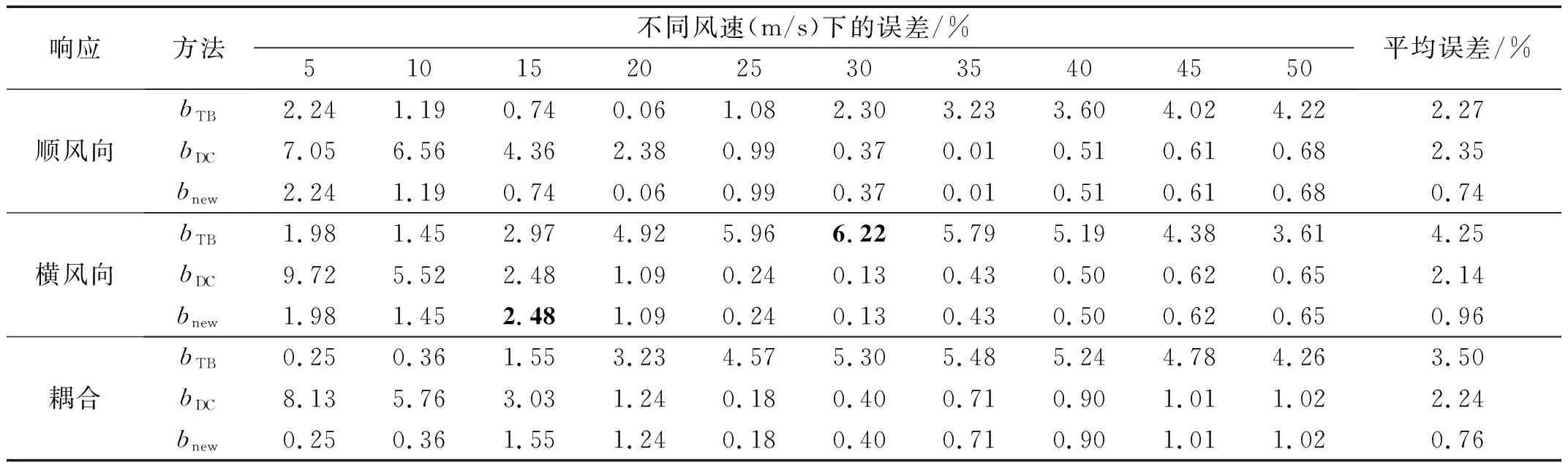
表1 T-B谱方法及其改进方法与雨流法误差(m=3, ζ=0.01)

表2 T-B谱方法及其改进方法与雨流法误差(m=4, ζ=0.01)

表3 T-B谱方法及其改进方法与雨流法误差(m=5, ζ=0.01)

由表1～表4可知，T-B谱方法的关键是确定参数b。研究通过数值模拟获得了新的b值表达式，结果表明其能更好地预测风致疲劳损伤。

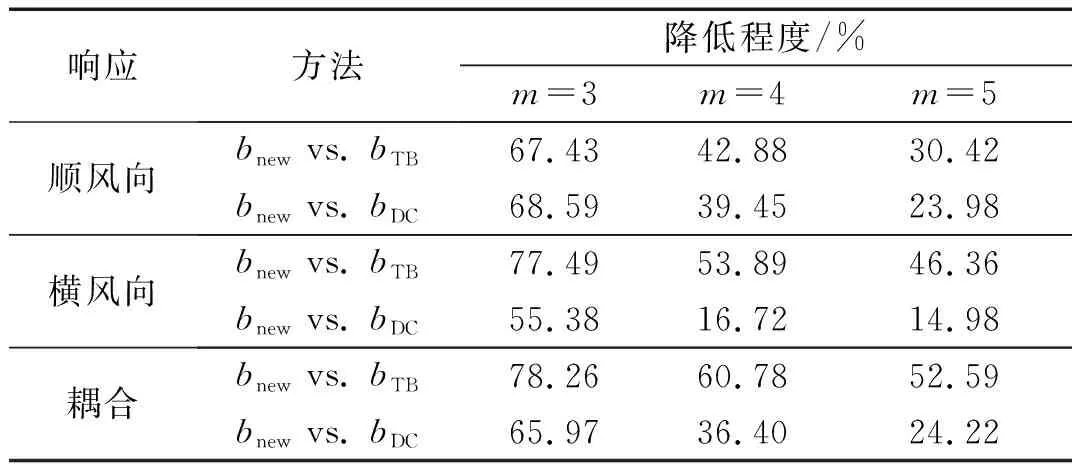
表4 改进方法相对原有T-B谱方法平均误差的降低 程度(ζ=0.01)

3 结 论

本文以高层建筑顺风向、横风向以及耦合风振疲劳损伤为研究对象，并以时域雨流法为基准，首先评价了原有两种T-B谱方法的计算精度；其次，基于该方法关键参数的分析结果，并结合数值模拟，给出了该参数的包络值；最后，基于该包络值提出了改进的T-B谱方法，同时验证了其有效性。通过上述研究，得出以下结论：

(1) 相比时域雨流法而言，原有两种频域T-B谱方法依旧有效。然而，随着反映材料疲劳特性曲线(S-N曲线)的斜率参数增加，其与雨流法之间的误差越来越明显，甚至超过20%；

(2) 相比原有两种T-B谱方法，改进方法更接近雨流法计算结果，以横风向且材料S-N曲线斜率参数m=3的结果为例，其平均误降低程度分别为77.49%和55.38%；

(3) 值得说明的是，根据各国规范可知，钢材S-N曲线的斜率参数取值主要为3[18]。此时，改进T-B谱方法计算所得疲劳损伤与雨流法之间的误差均在2.5%的范围内。由此可知，该方法在实际工程中具有一定的意义。

附录A

文献[20]表明响应的时距对雨流法计算结果影响较大，其中，由于顺风向响应具有最宽的带宽参数(见图1)，因此其要求的合理时距最长，如图A1所示。同时，相比常规建筑物而言，高层建筑阻尼比较小，因而其达到振动稳态所需时间更长。为保证雨流法的准确性且避免瞬态响应的干扰，本文模拟样本的总时距取8 000 s。其中，样本有效时距长度为6 000 s。

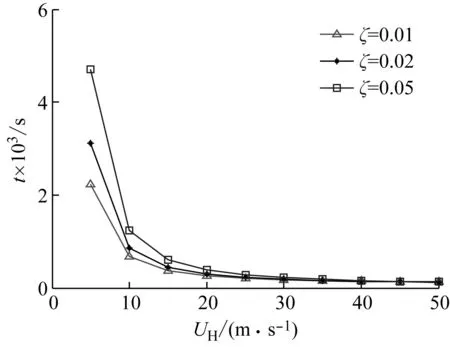
图A.1 顺风向响应下保证雨流法正确性的合理时距