快关蝶阀密封副瞬态热及碰撞冲击研究

李树勋， 杨玲霞， 雒相垚， 尹会全

(1.兰州理工大学 石油化工学院，兰州 730050；2.机械工业泵及特殊阀门工程研究中心，兰州 730050)

近年来随着冶金、火电、核电、石油化工等行业紧急切断系统的大容量、高参数与大型化，对其安保系统的安全性和可靠性要求也越来越高，快关蝶阀作为切断类阀门，其可靠性主要取决于其密封性及抗冲击能力[1-2]。高温蝶阀较大的温差载荷及冲击力，引起蝶板与阀座变形不一致与密封面破坏，引起密封失效发生泄漏事故[3]。

相关学者通过有限元法对热效应对密封的影响规律进行了研究[4-9]，徐自力等[10]采用有限元研究汽轮机在起动过程中不同温升分配方案对转子最大热应力的影响，发现选择合理的温升分配模式可以有效降低起动过程转子热应力。张雨等[11]对旋转效应和热效应造成导致密封性能变化的影响规律进行了研究，表明旋转效应和热效应减小了迷宫密封间隙宽度；高斌超等[12]分别建立了接触式机械密封的稳态和瞬态模型，分析稳态密封与瞬态密封性能之间的演化规律，提出了控制机械密封环变形的设计方法。Fatu等[13]开发了一种瞬态模型来模拟包含起伏的旋转唇形密封件的弹性流体动力学行为，分析了等温条件下密封唇的弹性变形；黄运生等[14-15]分别通过有限元法对冲击载荷对铁路轴箱轴承和泡沫救生舱安全性进行分析研究；张敏等[16]基于上限定理，对四周固支矩形板在楔形物垂向撞击下的塑性大变形响应进行了理论分析和试验研究，表明所提解析方法有较好的计算精度；Mikhailova等[17]构造了具有填充物的壳体系的瞬态函数，得到了由壳体系统与地基之间的碰撞导致的基本解析微分方程，并描述了解析解的数值分析算法。Zhang等[18]提出了一种有限差分模型与理论接触模型相结合的混合数值分析模型来研究受到球体撞击的简支梁的瞬态响应，并进行实验验证。Liu等[19]对几种软材料在平面正面冲击条件下进行了跌落冲击试验，并从黏性瞬变现象的角度研究了材料的冲击力波形发生机理。Rout等[20]使用采用有限元法对不同的加筋组合进行了预应力分析，并对分层复合材料加筋壳体的低速冲击响应进行研究。

国内外研究大多关注的是瞬态热及直行程碰撞冲击造成的结构磨损疲劳及密封失效问题，对瞬态热作用下的旋转类快关阀门密封副的研究很少。文章采用数值仿真方法对快关蝶阀分别进行瞬态热-结构耦合及瞬态动力学分析，对比研究不同升温速率、不同关闭速度及不同密封面宽度对快关蝶阀结构强度及阀座密封性能的影响，为快关蝶阀的密封优化设计提供参考。

1 研究对象及基本参数

如图1所示为高温快关蝶阀结构，技术参数如表1和表2所示。

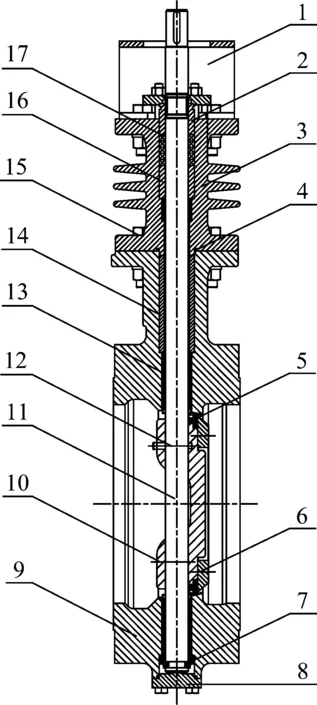
1.支架；2.填料压盖；3.散热架；4.阀盖；5.密封圈；6.阀板圈；7.推力轴承；8.底盖；9.阀体；10.阀板；11.阀杆；12.圆锥销；13.轴承；14.压环；15.螺母；16.压环；17.填料

表1 技术参数

表2 快关蝶阀主体材料

2 数学模型

2.1 瞬态热-结构耦合有限元理论

根据能量守恒定律和傅里叶传热定律，建立快关蝶阀的热传导控制方程，即阀门瞬态温度场T(x,y,z,t)应满足以下方程

(1)

式中：ρ为材料密度,kg/m3；cT为材料比热,J/(kg·K)；κx、κy、κz分别为沿x、y、z方向的热传导系数,W/(m·K)；Q(x,y,z,t)为物体内部的热源强度,W/m3。

该快关蝶阀的传热方程为

{q}T{η}=-hf(TB-TS)

(2)

TS=f(x,y,z,t)，t>0

(3)

式中：{q}为热流密度向量；{η}为边界面上外法线方向的单位矢量；hf为对流换热系数；TB为环境介质温度；TS为与物体接触的流体温度。

有限元法计算瞬态温度场的基本方程式为

(4)

式中：Δt为时间步长；{T}t-Δt为初始时刻的温度场；{T}t为t时刻的温度场。

以应变、温度表示应力的广义虎克定律

(5)

结合位移方程、变形协调方程、几何方程以及边界条件根据独立的方程以及温度t的变化，就可以求解出在温度场与应力场耦合作用下的6个热应力分量，对于高温阀门，阀体及内件承受的热冲击和介质冲击载荷会在结构中产生较高应变率，使得结构的热耦合项作用增强。

2.2 快关蝶阀密封副冲击模型

快关蝶阀在快速关闭过程中，蝶板和阀座密封面承受快速撞击，蝶板及阀座的碰撞面发生了较大的弹性和塑性变形，按照变形的情况可分成压缩区、剪切区、剪切拉伸区及胀大区，如图2所示[21]

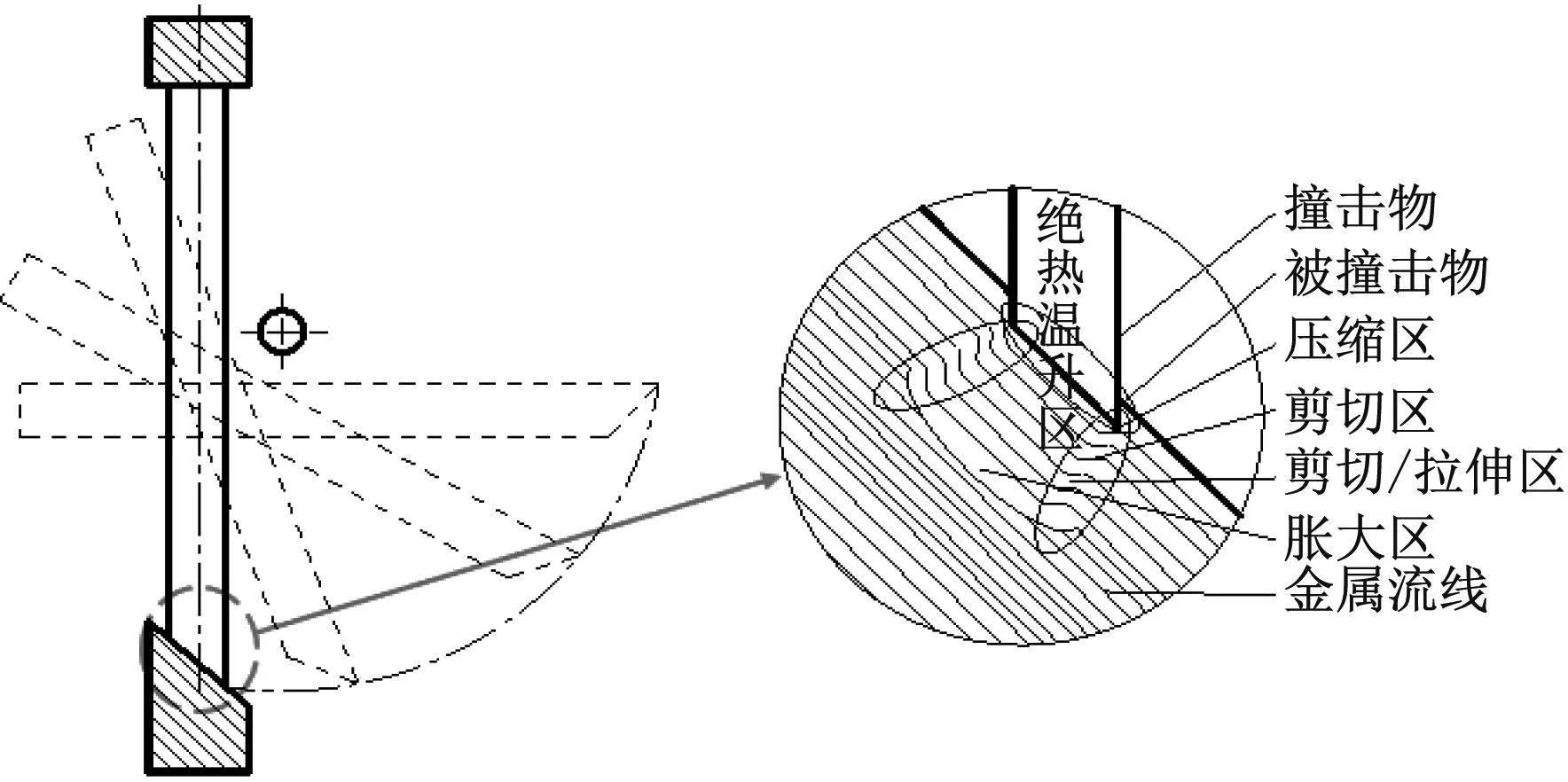
图2 快关蝶阀冲击示意图

根据动量矩定理

J(w-w0)=TΔt

(6)

T=Fr

(7)

为简化计算，用椭圆柱体的转动惯量近似代替，椭圆柱体的转动惯量计算公式如下

(8)

式中：J为蝶板及其转动部件的转动惯量；w为蝶板运动的角速度；T为转矩；F为冲击力；r即为中心轴距阀座密封面间的距离；Δt为速度由主轴旋转速度减到零的时间差。

联合式(6)、(7)与式(8)可得旋转冲击力计算式为

(9)

快关蝶阀关闭瞬间，阀座及蝶板密封面受冲击力作用。对冲击时蝶板密封锥面最大锥角处进行受力分析如图3所示。蝶板斜锥面受到切向反作用力F，法向冲击分力F1对结构强度的影响最大，忽略对结构影响较小水平冲击分力T。假设三偏心锥角为θ，则F1为

F1=Ftanθ

(10)

图3 蝶板受力示意图

单位面积所受冲击应力为

(11)

式中：S为蝶板密封锥面的环面面积，可由蝶板外表面曲面方程式(11)求得，密封面环面面积示意图如图4所示。

图4 圆截面蝶板结构

(12)

综合上述公式将相关参数代入可得快关瞬间冲击应力为104.27 MPa。根据式(11)，冲击应力主要与密封环面积S有关，而法向冲击力F1取决于总的旋转冲击力F和锥角θ，当θ恒定时，F与J、ω、Δt、r相关联。

3 快关蝶阀三维及网格模型的建立

建立快关蝶阀三维模型并进行网格划分，对蝶阀和阀座的冲击接触面进行网格加密处理为0.1 mm。通过网格无关性检验最终确定网格模型的单元数目为586 408。三维及网格模型如图5所示。

图5 快关蝶阀三维及网格划分模型

4 瞬态密封数值模拟分析

考虑阀门在高温工况下，阀内壁温度较高，阀座圈和蝶板密封面会产生变形不一致导致密封失效，对阀门进行高温下密封接触非线性有限元分析。阀体内表面施加温度载荷550 ℃；阀体外表面保温层设置绝热，阀门保温层以外和空气接触的部位设置对流换热系数为25 W/(m2·K)。瞬态分析时根据实际载荷确定载荷步，设置两个载荷步。第一个载荷步设置瞬间升温至472 ℃，第二个载荷步设置温度径向传递过程，温度仍为472 ℃，传递时间为5 400 s，设置500个载荷子步进行计算。

4.1 瞬态温度场分析

通过瞬态温度场计算，得到快关蝶阀的温度场信息，为研究快关蝶阀瞬态温度变化情况，提取填料函处、阀杆上端、阀盖法兰边缘、阀盖散热片处、阀体内外壁及进出口端8个位置节点作为观察点，绘制8个节点温度时程曲线，分析温度随时间变化的规律，具体如图6所示。

图6 快关蝶阀不同节点温度时程曲线

由图6可知，阀体内壁迅速升温至480 ℃，阀体外壁因有保温措施，节点1、2、8处温度在1 000 s内呈直线迅速上升且接近472 ℃，而后逐渐趋于稳定；节点3、4、5、6离阀体较远，温度上升较慢，约在1 500 s后逐步趋于稳定，节点4稳定后的温度约为26 ℃，满足填料函使用温度；因此，快关蝶阀瞬态热密封分析只需研究1 500 s内，即径向热传递时间内的温度场分析即可。

4.2 升温速率对快关蝶阀密封副影响研究

根据高温快关蝶阀工作时的升温过程，同时参考文献[22]的升温方案，分析不同升温速率下蝶阀的温度场分布，对于升温及温度径向传递时间具体分配方案如表3所示。后期计算表明，采用的升温及温度径向传递时间均能保证瞬态分析的最终温度与稳态温度场相近，为不同升温速率下瞬态耦合密封计算的准确性提供保障。

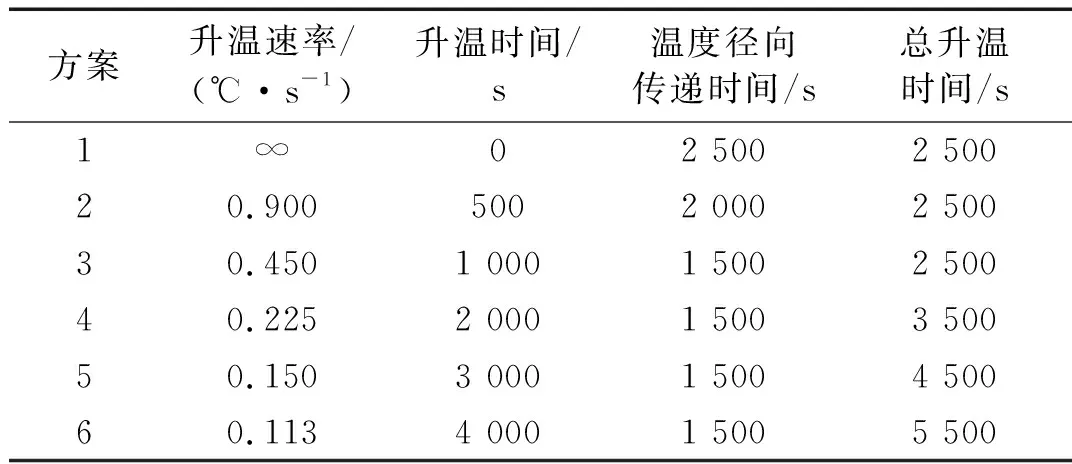
表3 不同升温速率瞬态热分析方案

不同升温率方案下瞬态最终温度与稳态温度相比误差较小，如图7所示，误差在0.3%～1.5%，远小于5%，瞬态温度分析结果表明，采用的分配方案均能保证瞬态分析的最终温度与稳态温度场相近，保证了瞬态耦合密封计算的准确性。

图7 不同升温率下瞬态最终温度与稳态对比

通过瞬态热-结构耦合分析，不同升温速率方案对应的阀座密封面最大接触压力时程曲线如图8所示。

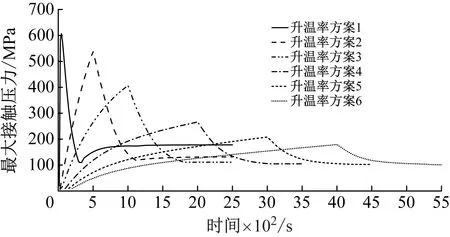
图8 不同升温速率下密封面最大接触压力时程曲线

由图8可知，针对表3中总时间均为2 500 s的方案1、2、3，方案1接触压力骤然增大后迅速降低至最小值又略微回升并保持稳定。方案2、3与方案1的接触压力变化趋势一致，升降温速率较方案1缓和。3个方案最大接触压力分别为606.59 MPa、539.99 MPa、406.58 MPa，均超过材料的许用比压，其下降至最小值所用时间逐渐增加，对应最小接触压力分别为138.04 MPa、130.14 MPa、110.87 MPa，由此可知升温率越大，瞬间峰值接触压力越大且下降越快，对应最小接触压力越大。分析表2径向温度传递时间均为1 500 s的方案3、4、5和6，观察4条曲线，方案3接触压力先升高后降低趋势最为显著；方案4、5、6变化趋势较为缓和，分别在2 000 s、3 000 s及4 000 s降低并渐趋于一稳定值，分别为104.73 MPa、102.35 MPa、100.88 MPa，峰值接触压力分别为266.10 MPa、208.24 MPa、179.36 MPa，单位时间内接触压力差值越小，随升温时间的延长，升温过程中结构温差越小，热应力越小。

对比图8中的6条曲线，可知随温度的升高，快关蝶阀密封面最大接触压力均先升后降到一定温度值并趋于稳定，升温速率越小，接触压力的变化越平缓。升温时间超过2 000 s时，最终接触压力值均小于材料的许用比压，差值较小，峰值接触压力只在升温时间大于3 000 s时小于材料许用比压。各升温率对应的最终接触压力分布云图如图9所示。

图9 不同内壁升温速率下最终接触压力分布云图

分析图9可知，随着升温率的减小，接触压力的最大值位置逐渐由密封锥面直角侧向斜锥侧转移，具有相似的接触压力分布，最终结果均满足密封要求。

结合图8，接触压力与稳态分析结果相差百分比分别为27%、12%、8%、4.4%、1.70%、0.76%，由此可见，对于本文所研究的DN200、PN16具有保温层型式的快关蝶阀，工作温度为472℃时，若用稳态热-结构耦合分析，最大接触压力误差允许在5.0%以内时，则该阀门升温时间至少应为2 000 s，即内壁升温速率应低于0.225 ℃/s。

5 冲击动响应模拟分析

根据设计要求对快关蝶阀进行瞬态动力学分析计算时设定条件如下：设置关闭时间0.5 s，冲击时间设为0.1 s，；载荷步设为两步，第一个载荷步设为0～0.5 s，载荷子步为180步；第二个载荷步设为0.5～0.6 s，为得到精确的冲击应力变化过程，载荷子步设置5 000步。

5.1 瞬态冲击对快关蝶阀影响分析

快关冲击时初始能量由冲击动能和蝶板位能两部分组成，对快关蝶阀进行冲击能量分析，说明冲击能量的转化与耗散趋势，快关能量时程曲线如图10所示。

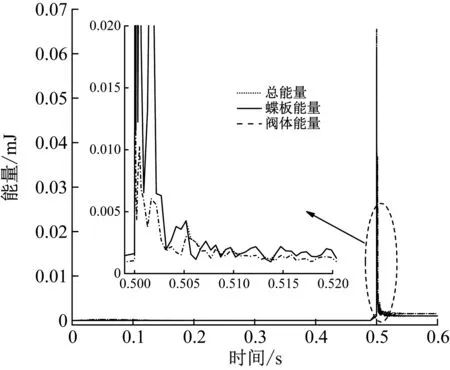
图10 快关能量时程曲线

碰撞冲击过程能量耗散部分主要包括损伤耗散、摩擦耗散、塑性耗散、应变能、黏性耗散、热能。图10中总能量和蝶板能量变化趋势相近，总能量在碰撞冲击10 ms内与蝶板能量几乎一样，后期蝶板能量衰减振荡幅度大于总能量，最终在0.01 s内能量波动幅度渐趋稳定。

由图11可知，在关闭后0.06 ms时应力达到最大，最大应力为105.87 MPa，与第二章理论计算结果相差1.5%。蝶阀的应力随冲击时间的变化呈衰减振荡并趋于稳定。

图11 最大应力时程曲线

为研究快关冲击行为对阀座与蝶板密封面的影响，在蝶板与阀座密封接触面中间部位等距取8个节点进行检测，得到快关过程中阀座、蝶板密封面上的节点应力时程曲线，如图12、13所示。

图12 阀座密封面节点应力时程曲线

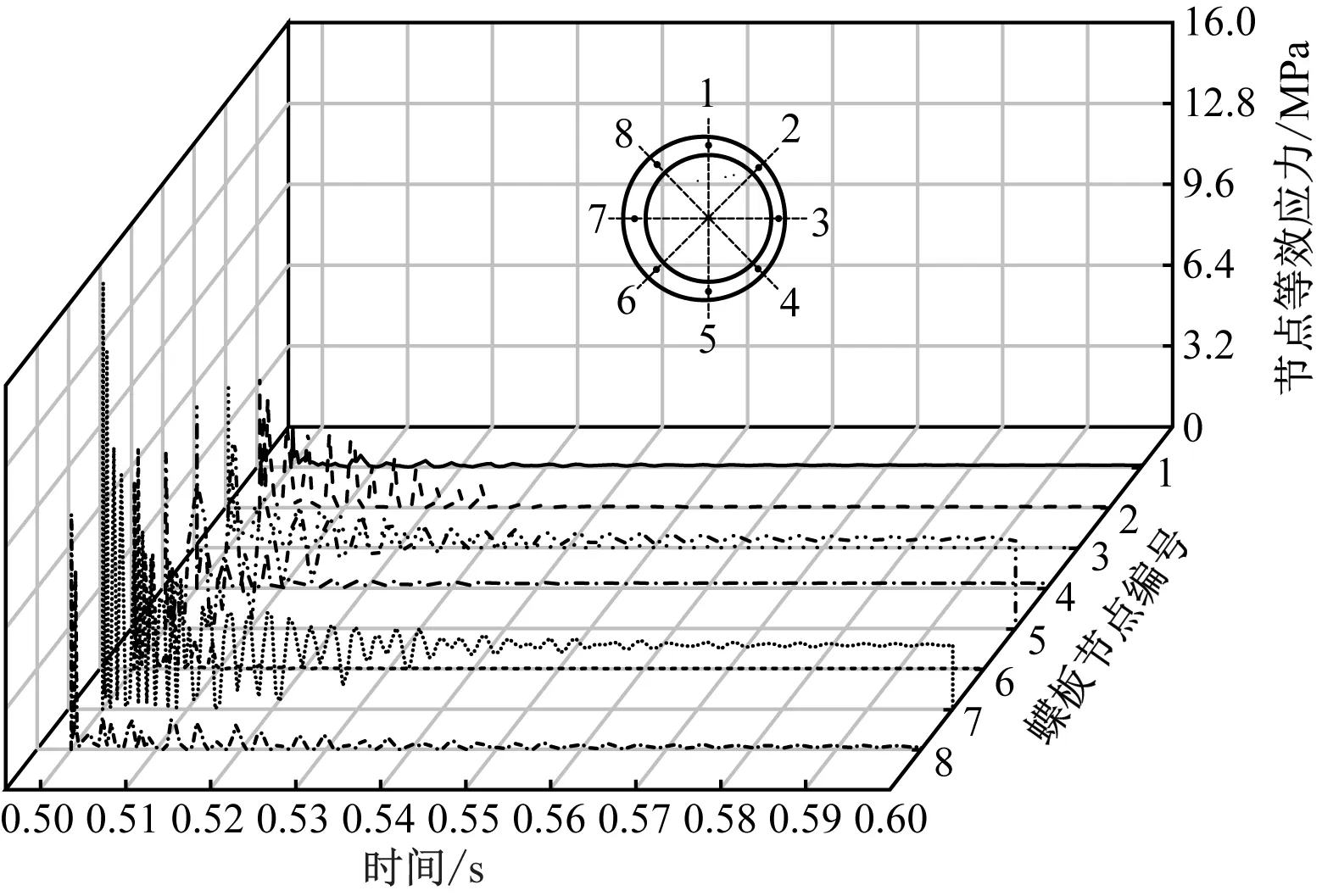
图13 蝶板密封面节点应力时程曲线

由图12、13可知，8个节点中，节点7位于阀座密封斜锥面锥度最大处，其冲击应力波动幅值最大，其他节点的较小。快关过程中8个节点应力变化趋势基本相同，均在碰撞瞬间应力急剧增大，然后经振荡趋于稳定。快关过程中蝶板密封面节点应力波动幅度大于阀座密封面节点应力波动幅度，主要由于蝶板密封圈宽度比阀座宽度小，并且瞬间碰撞时，蝶板密封圈作为冲击物要承受更大的冲击反作用力。

由图14可知，0.5 s时刻蝶板撞击阀座，快关冲击瞬间密封面接触压力急剧增大至126.05 MPa，而后接触压力呈衰减振荡趋势，逐渐稳定在62 MPa左右，大于必需比压7.3 MPa，小于密封材料许用比压，密封性能满足要求。

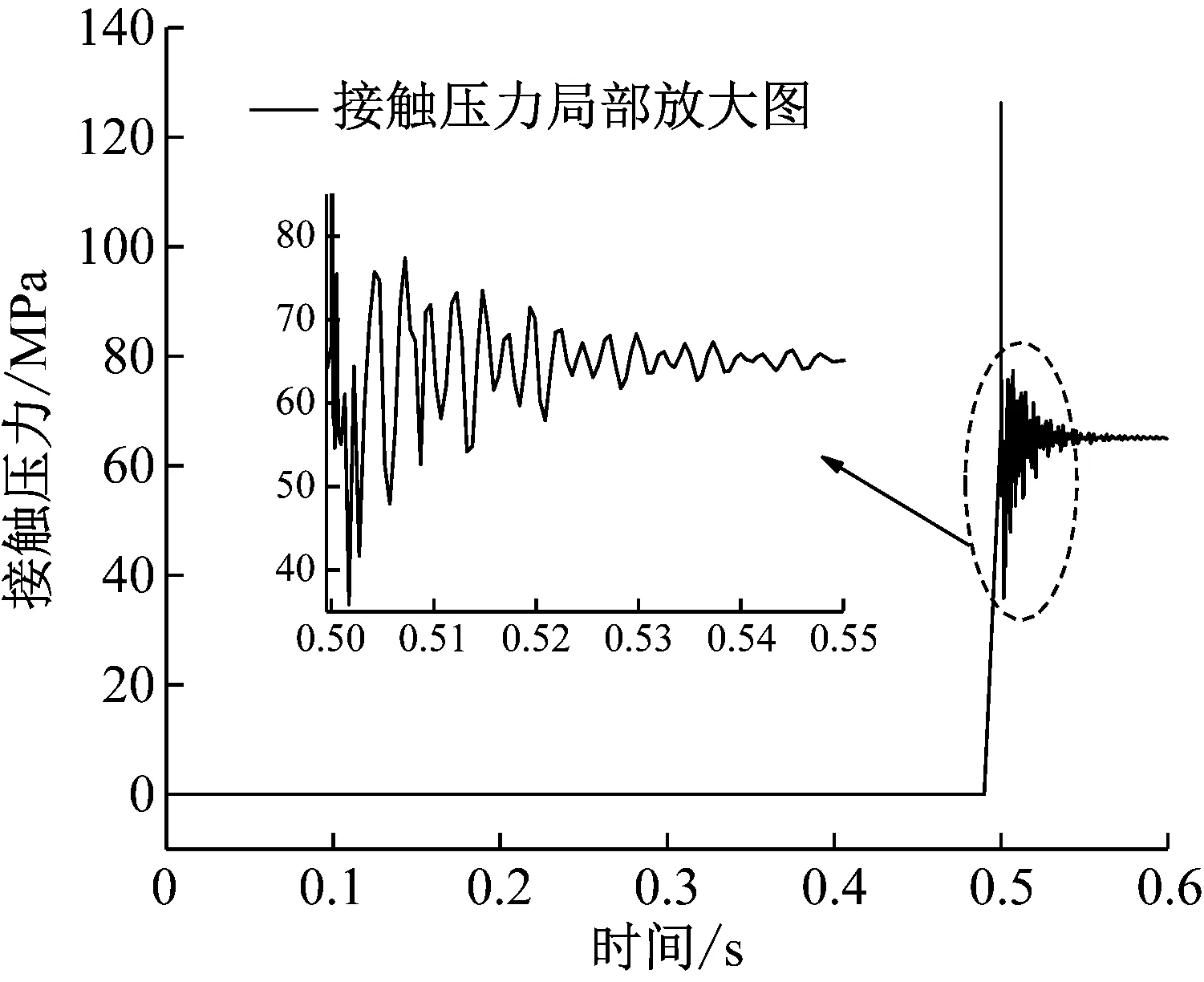
图14 最大接触压力时程曲线

5.2 冲击速度对快关蝶阀密封副的影响

通过对快关蝶阀进行不同快关时间(0.3 s、0.4 s、0.5 s、0.7 s、1 s)工况下的瞬态动力学分析，得到不同快关时间对应的应力时程曲线及不同关闭时间对应的接触压力变化曲线如图15、16所示。

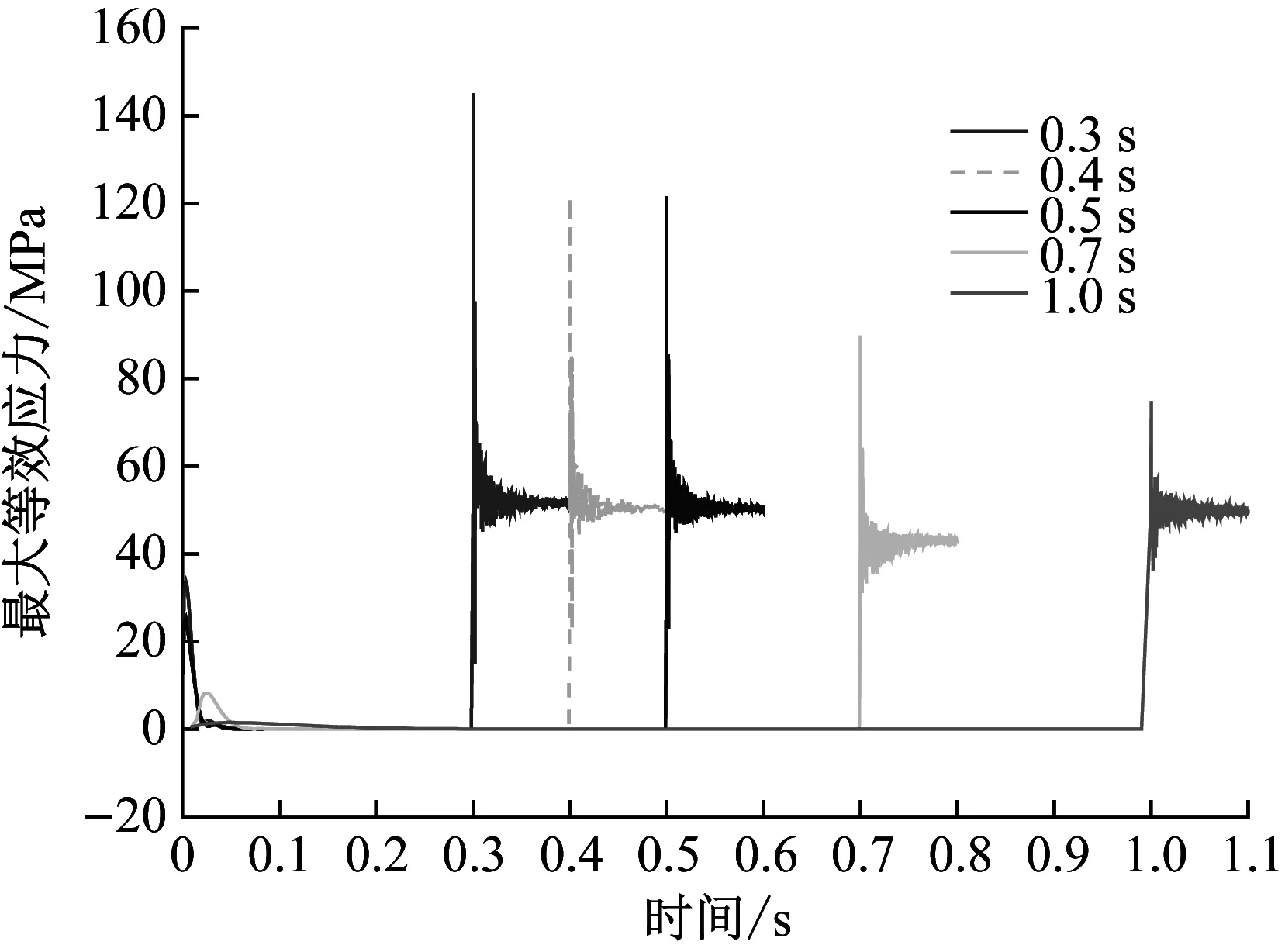
图15 不同快关时间下冲击应力时程曲线

图16 不同快关时间下接触压力时程曲线

图15中，在关闭初期50 ms内均出现应力小幅度升高又降低至零，在关闭瞬间应力急剧增大到峰值，应力呈现不规则振荡衰减并渐趋稳定。(0.3 s、0.4 s、0.5 s、0.7 s、1 s)对应最大冲击应力分别为145.17 MPa、123.69 MPa、105.87 MPa、90.17 MPa、77.61 MPa，最终稳定值为50.25 MPa、51.87 MPa、49.74 MPa、42.06 MPa、52.15 MPa。0.3 s、0.4 s最大冲击应力超过材料的许用应力。可见，不同快关时间内快关蝶阀的冲击应力变化趋势基本一致，冲击速度越大，瞬态冲击应力越大。

由图16可知，在关闭瞬间，接触压力急剧增大到峰值，而后呈现不规则振荡并逐渐衰减至一稳定值，(0.3 s、0.4 s、0.5 s、0.7 s、1 s)最大接触压力分别为169.89 MPa、143.49 MPa、126.05 MPa、102.11 MPa、86.51 MPa，均小于材料的许用比压。最终稳定值为62.75 MPa、62.84 MPa、61.95 MPa、64.86 MPa、63.75 MPa，可见，不同快关时间内快关蝶阀的接触压力变化趋势基本一致，在关闭瞬间，密封面接触压力急剧增大到最大值，且随快关时间的增大而减小，随着时间的推移在0.1 s内波动达到稳定值。快关时间越短，密封面上的瞬间峰值接触压力越大。

5.3 碰撞面积对快关蝶阀密封副的影响

为研究不同撞击面积对快关蝶阀冲击行为的影响程度，选取1 mm、3 mm和7 mm共3个不同冲击面积方案，分别对三种方案的蝶阀密封副冲击进行对比研究，得到不同密封面宽度对应的最大冲击应力云图、应力时程曲线图及接触压力变化曲线图如图17、18所示。

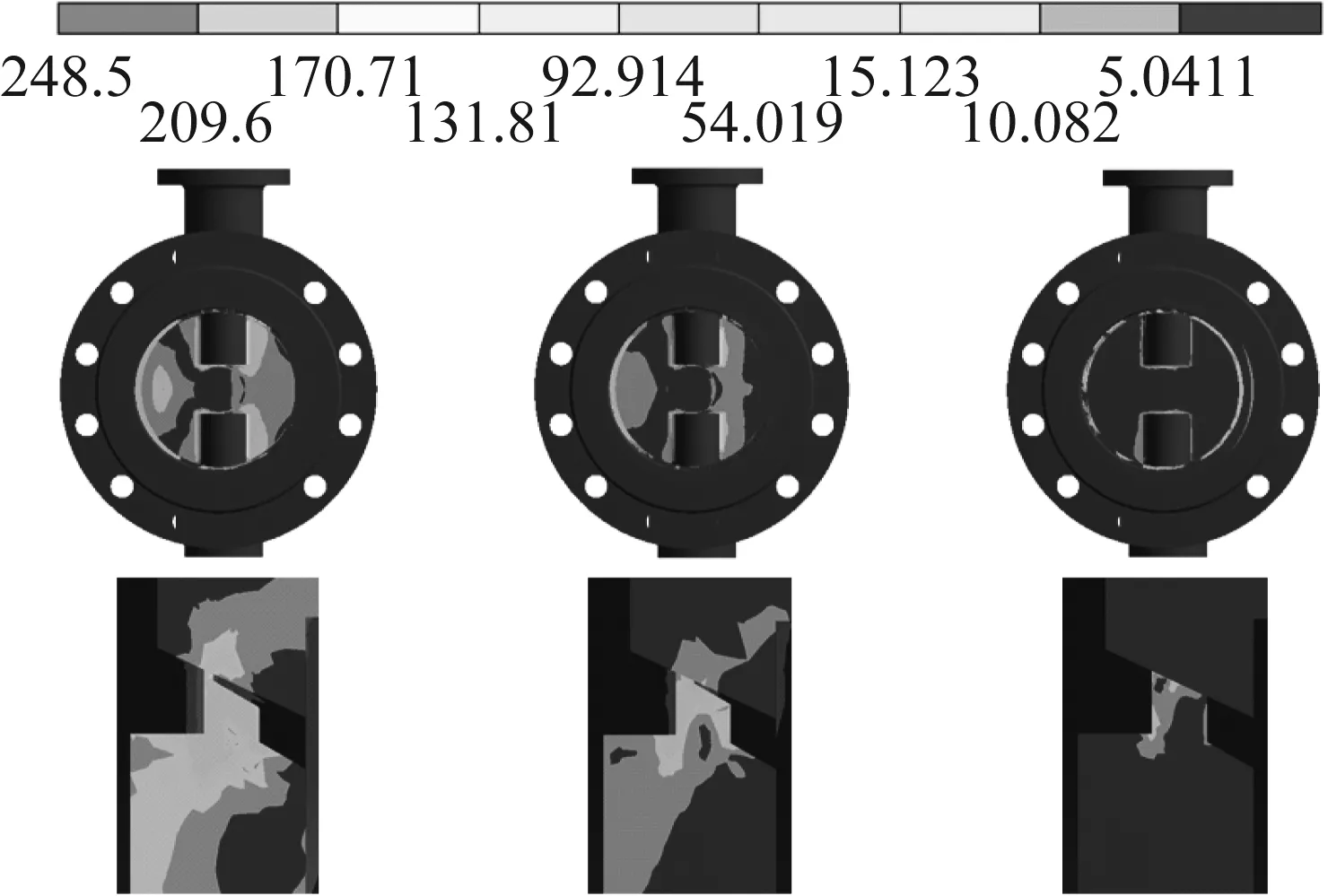
图17 不同密封面宽度下最大冲击等效应力分布云图

图18 不同密封面宽度下最大等效应力时程曲线

结合图17、18，快关瞬间产生的最大冲击应力在密封面最大锥角处，随着密封面宽度的增加(1 mm、3 mm和7 mm)，撞击面积增大，最大冲击应力变小，分别为248.50 MPa、105.87 MPa、64.05 MPa，冲击影响区域变小，然后在0.5～0.6 s时间内应力不规则振荡并逐渐衰减至一稳定值分别为98.41 MPa、51.72 MPa、48.97 MPa。冲击应力振荡稳定时间与接触面积成反比，密封面面积越小，冲击应力振荡及稳定所需时间越长，冲击应力越大，蝶阀的安全裕度越小。

6 结 论

(1) 同一升温速率工况下热应力及接触压力均呈现先升后降的趋势，升温速率越大，趋势越明显，热应力及接触压力越大。升温过快时，峰值热应力与接触压力及最终热应力与接触压力均会超过材料的屈服极限。针对文章研究的PN16、DN200高温快关蝶阀，当阀门内壁升温速率小于0.225 ℃/s时，阀门的结构强度及密封均可满足要求。

(2) 对快关蝶阀冲击过程瞬态受力进行了理论推导，得出了冲击应力与转动惯量、阀轴转速、阀杆与阀座间的距离及冲击力作用时间等参数之间的关系。进行了理论冲击应力计算，并与数值仿真模拟值对比相差为1.5%，为蝶阀的冲击计算提供理论指导意义。

(3) 快关过程中，蝶板密封面处的应力变化趋势在碰撞时刻应力快速增大，而后振荡衰减趋于稳定，其中蝶板密封锥面斜度最大处冲击应力波动幅值最大，且大于阀座密封面。碰撞冲击应力与阀座密封面接触压力均随冲击速度的增大而增大，随接触面积的减小而增大。冲击速度对冲击的影响较大，撞击面积较小，为快关蝶阀结构参数及冲击参数的设计提供参考。