基于注塑机螺杆位置与压力曲线的注射成型过程监测方法

0 引 言

注射成型是塑料熔体在温度、压力作用下材料状态发生复杂变化的过程，成型过程与制品质量存在非线性、强耦合和时变性的关系，导致制品成型质量较预测困难

。随着传感技术与计算机嵌入系统的发展，注塑机或模具内的传感器在成型过程中记录了大量的过程曲线数据，包括螺杆位置、速度、温度和压力等，这些数据蕴含了注射成型过程质量信息

。由于曲线数据维度高，难以直接通过这些曲线数据获取足够的注射成型过程信息。近年来，人工智能方法促进了数据降维以及模式识别的发展，使从高维度数据建立成型过程质量关系成为可能。

以前注射成型过程监控主要采用主成分分析法（principal component analysis，PCA），在假定变量独立分布且服从正态分布条件下，将多个变量通过线性变换得到重要变量，去除原始数据的冗余信息

。主成分分析法仅适用于连续工业生产过程的二维数据，而塑料熔体注射成型是典型间歇性生产过程，一般采用多向主成分分析法将曲线变量、时间和批次构成的三维结构展开为二维结构

。如YI X H等

通过多向主成分分析法分析了保压、注射2个阶段的螺杆位置和压力曲线，并开发塑料熔体注射成型的过程检测系统。但是主成分分析法和多向主成分分析法本质上都是一种线性变换，它们要求变量之间相互独立且服从正态分布的假设与塑料熔体注射成型过程非线性、强耦合的实际情况不相符。YUN Z等

将统计分析法（statistic pattern，SP）引入注射成型过程监控，通过提取曲线数据的统计量，将数据从930维降至26维后再使用主成分分析法建立监控模型，解决了上述问题，但由于统计分析法仅考虑变量之间的整体统计因子，没有考虑实际变量参数之间的联系，丢失了较多的数据信息。

现分别使用主成分分析法和3种非线性法，即统计分析法、拉普拉斯映射（laplace eigenmaps，LE）法、扩散系数图（diffusion maps，DM）法对塑料熔体注射成型过程进行数据降维和特征提取，然后通过神经网络模型建立特征数据与制品成型质量之间的关系模型，研究塑料熔体注射成型过程的监控技术。

1 注塑机曲线的降维与监测模型

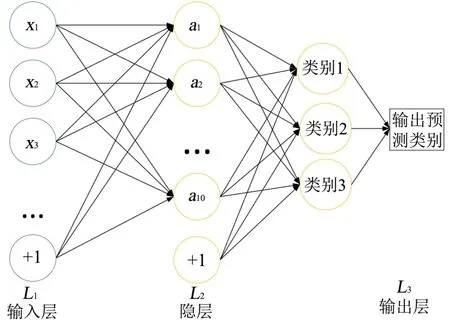
注塑机曲线的降维与监测模型如图1所示，首先通过注塑机获得螺杆的压力和位置曲线的原始数据，进行预处理后分别采用4种方法降维后输入神经网络，完成塑料原料监测、模具温度监测和成型制品质量预测的功能。

主持人：近日，习近平总书记、李克强总理、多部委负责人频频为民营企业发声，支持民营经济发展，一系列针对性举措密集出台，这释放了什么信号？在我国经济步入高质量发展轨道的背景下，民营企业面临着哪些困难和挑战？

1.1 数据采集与预处理

注射成型过程的主要控制变量包括熔体温度、注射位置、注射速度和注射压力等，因此理论上需要采集熔体的温度曲线、螺杆的位置、速度和压力曲线。考虑注塑机的温度传感器安装在料筒外壁，塑料熔体热导率低导致测量温度数据滞后性较大，温度曲线不是一种实时监测曲线。同时塑料熔体的温度、压力和体积必须满足PVT方程，因此温度曲线的信息可以通过螺杆的位置（体积）和压力曲线间接反映，此外螺杆的速度是其位置的一阶导数，注塑机监测曲线选择螺杆位置和压力曲线。

为了避免监测变量曲线范围差异对后续分析的影响，需要对数据进行归一化预处理。数据归一化是数据建模前重要的数据处理步骤，包括样本尺度归一化、逐样本的均值相减和特征标准化3种。逐样本的均值相减主要应用于稳定性的数据集中，即数据每个维度间的统计性质是一样的情况，而注射成型过程中螺杆位置和压力在不同时刻信息不同，此方法不适用。特征标准化是指对数据的每一维进行均值化和方差相等化，常用的数据标准化方法有：Z标准化、最大值-最小值标准化、Log函数标准化等。根据数据特征，采用Z标准化方法，基于统计理论的偏差标准化，使经过处理的数据符合标准正态分布，即均值为0，标准差为1，处理步骤如下。

（1）中心化处理，即去均值，消除自身变异、数值大小带来的影响，即

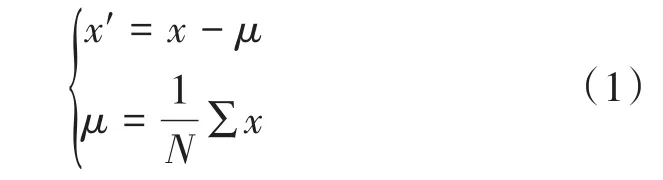
式中：

——原始螺杆位置或压力；

——相应中心化处理后的数据；

——曲线采样点数；

——采样数值均值。

（2）无量纲化处理，即

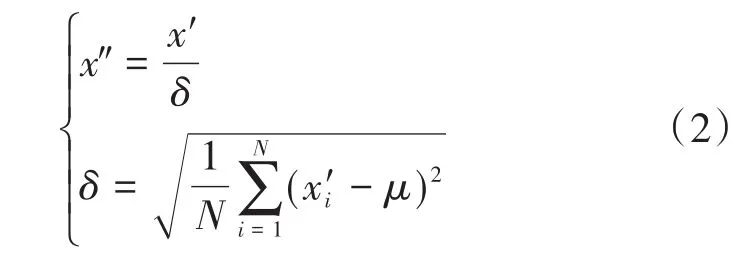
式中：

——无量纲化处理后的数据；

——采样数值均方根误差。

通过旅行，我学到了很多地理和历史知识。为了与人交流，我学会了英语、西班牙语和越南语。在越南待了7年之后，可以说我对这个国家的了解要甚于我对自己的了解。

1.2 数据降维方法

质量预测模型最后输出一个具体的数字，而不是类别，即如果故障监测是一个离散的输出，质量预测就是一个连续输出。模型的设计层数确定、隐藏神经单元与故障监测一致，与故障监测最后的Softmax分类器不同，质量预测采用的是拟合器。

（1）主成分分析法。主成分分析法是将高维度数据空间通过线性变换投影到低维度主成分空间，选出较少个数的重要变量的多元统计分析方法

。它去除了原始数据中的冗余信息，是有效的数据压缩和信息提取的方法。主成分分析法适用于二维数据矩阵

(

×

)，其中

是数据样本的个数，

是数据维度，得到得分向量、负载向量、特征值，即

经 FPD检测器检测，发现样品图谱中分别含有出峰时间相互对应的 3个峰，通过与有机磷类农药标样检测图谱的出峰时间进行比对，确定检出的农药组分分别为敌敌畏、氧化乐果、甲基对硫磷。经ECD检测器检测，发现样品图谱中含有出峰时间相对应的 4个峰，通过与有机氯类农药标样检测图谱的出峰时间进行比对，确定检出的农药组分分别是乙烯菌核利、联苯菊酯、氯氰菊酯、氰戊菊酯。

(2)次生地质灾害严重，道路、电力、通讯全面受阻，救援生命线修复艰难。云南地震带与河谷叠合，地震区多为高山峡谷区，地震常造成巨型次生地质灾害，道路打通极为困难。余震、降雨又会诱发新的地质灾害，造成交通再次阻断，伤员转运困难，滞留在重灾区转运不出去。生活物资因地震被毁，而救援物资又难以进入灾区，造成交通大堵塞，大量救灾物资停留在重灾区10 km左右，而灾区物资又十分缺乏，且救援的核心之一医护人员难以第一时间到达灾区。

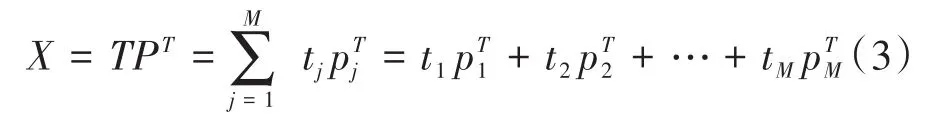
式中：

得分向量；

——负载向量。

此外，南充市旅游景点交通通达性呈现一定的规律特征：城市景区通达性优于乡镇景区通达性，平地景区通达性普遍优于山丘景区通达性，5A景区通达性明显优于4A及其以下等级景区通达性，原有景区通达性优于新建景区通达性。区域经济发展水平以及景点的知名度对旅游景点的整体交通网络可达性指数影响较大。

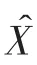
也因为漂亮，女人无法辜负这般人才。于是，她的所想所虑全都集中在了维持这份漂亮的穿着打扮上面。这么一来，小时候的书是很难读得好的，稍大一点又容易情窦早开，坠入男女的情感纠葛之中。而正是早恋早婚，其实还毫无社会与人生的经验，往往导致婚后不幸，命运多蹇。

式中：

——热核的宽度，其取值与邻域

相适应。

（2）统计分析法。统计分析法是一种利用数据统计信息完成对数据降维再现的一种信息处理、压缩和提取方法

。统计变量包括一阶统计量（平均值

）、二阶统计量（方差

）、三阶统计量（偏度

）、四阶统计量（峰度

）等，定义如下：

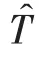
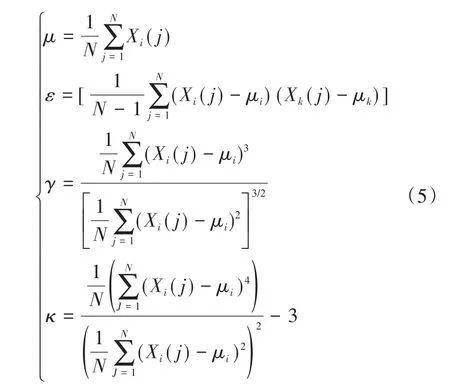
（3）拉普拉斯映射法。拉普拉斯映射法算法寻找一个低维度数据来保留流形数据的局部性质

。通过相邻2点之间的距离实现数据的低维度再现，通过权重的方式实现数据点之间的距离和

个近邻被最小化，即离得越近的点对于代价函数影响越大。使用稀疏光谱理论，将代价函数定义为特征问题，算法分为以下几步。

1）构建邻接图

，可采用近邻

法或

近邻法，即采用

近邻法。

2）定义近邻权矩阵

，可采用热核方式或简单连接方式，现采用热核方式，即若

x

和

x

相邻，那么

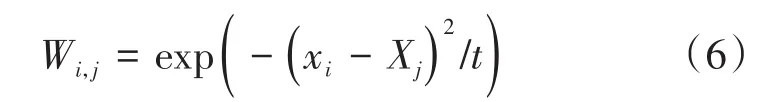
我国古代的藏书机构在不同时期，分别被称为“府”“观”“台”“阁”“殿”“院”“堂”“斋”“楼”等。我国有文字记载的最早的藏书机构是“盟府”和“藏室”。据《左传·襄公十一年》记载：“国之典也，藏在盟府。”是指东周时期各诸侯国建立盟府，用以掌管、储存盟约文书和典籍等。《史记·老子韩非列传》记载，老子“周守藏室之史也”。老子曾担任管理“藏室”的官吏。由此证明，“盟府”和“藏室”是中国历史古代文字记载的最早的藏书机构。

2）计算数据图，权重的连接使用高斯核函数。

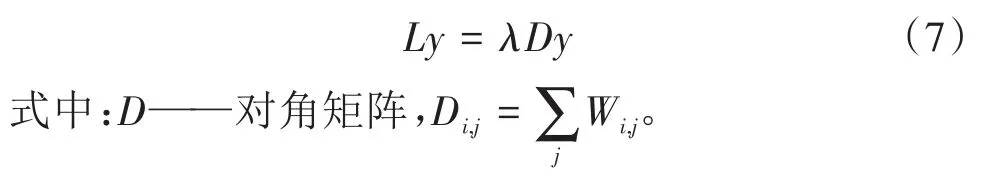
的最小

+1个特征值对应的特征向量

，

，…，

μ

构成了低维嵌入结果

=[

，

，…

μ

]

。该方法将降维和特征提取问题转化为对矩阵特征值和特征向量的求解，过程简单，无需迭代，因此计算量和计算时间减少。

（4）扩散系数图法。扩散系数图法同拉普拉斯映射法一样属于非线性降维方法，都是通过找到其隐藏的低维度空间数据结构，达到降维的目的。不同于拉普拉斯映射法基于邻近图的稀疏光谱分析，扩散系数图法是在保留局部性质的条件下基于分散距离的全光谱分析的降维方法

。扩散系数图法特征降维步骤如下。

1）进行下式的数据规范化，保证数据落在（0,1）。

朱俊玲《中国戏曲学院京剧经典剧目的传承与创新研究初探》[10]一文对中国戏曲学院对京剧经典剧目的传承与创新进行了简单总结：（1）基本保持原型，改动甚微的经典剧目；（2）融入新时代特色，改动较大的传统剧目；（3）贴近现代生活，完全新创的剧目。以上三类也是目前京剧剧目的创作现状。对于经典剧目与新创剧目，笔者就徐州民众对于京剧现代剧与传统剧的喜好进行了调查，有效问卷198份。其中有149位民众选择传统京剧，可见人们更偏爱经典故事。

3）构建拉普拉斯特征矩阵

=

-

，最小化特征映射误差，相当于计算下式中的最小特征向量。

式中：

——高斯方差。

3）计算矩阵

的行向量之和

。

定义了前向转移概率矩阵的Markov矩阵，表示在数据集中的一个数据点经一次转移至另一个数据点的过程。

式中：

P

——前向

次迭代的矩阵，可以通过其行向量之和定义扩散距离。

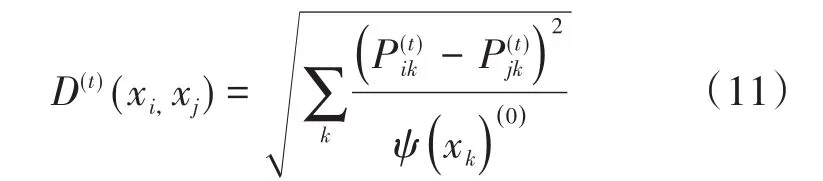
式中：

(

x

x

)——扩散距离；

(

x

)

——表示将更多的权重归因于高密度图的部分。

4）使用谱理论得到保留了扩散距离的低维度再现数据

。

由于图是全部链接的，最大特征值是平凡的，为1，被舍弃。再现数据

是

分主特征向量，即

={

,

,...,

λ

v

}。

1.3 故障监测与质量预测模型

可以通过不同降维方法提取数据特征以实现故障监测和质量预测，常用的有神经网络和支持向量机等。神经网络理论发展成熟

，支持向量机解决了神经网络存在的收敛速度慢、存在局部最小点等问题

，支持向量机在分类问题上具有优势，考虑存在分类和拟合两大方面，故采用神经网络作为建模方法。

律师称杨伟东被警方带走，并不能以此就认定其有罪。但他分析，消息爆出后阿里巴巴很快确认，并且应对有序，“当事人可能都不知道，但该知道的人或许早已知道，阿里内部很可能已经做了初步调查并掌握了一定的证据。而且杨伟东刚好在轮值结束后出事，要么是阿里真的非常幸运，要么是一切都在安排之中。”

故障监测的主要目的是实现对原材料和模具温度的故障诊断，采用分类器进行监测。神经网络层数越多，神经元数量越多，则训练精度越高，但是同时网络的泛化能力下降。为了取得较好的结果，根据应用场景，输入向量为降维后的数据，在20维左右，输出类型为3类。根据Kolmogorov定理，可采用三层神经网络结构。根据试验，发现神经元数量稳定在10个左右，分类函数选用Softmax分类器。故障监测的模型如图2所示。

注塑机螺杆的压力和速度在每一模内随时间变化，数据在时间和批次展开后维度高，直接计算成本大。降维处理是在尽可能保留原始信息的情况下，通过找出高维度的数据中占重要因素的点或者发现变量之间隐藏的关系，用较低维度的数据再现原始数据

。相比原始数据，降维后的数据不仅维数降低，而且更有可能反映原始数据不能体现的隐藏数据关系。现重点分析1种线性和3种非线性方法对数据进行降维。

2 试验设计

注射成型过程可以分为塑化、注射、保压和冷却4个阶段，这4个阶段决定了最终制品的成型质量，由于塑化的结果可以在注射和保压的过程控制曲线中体现，可以减去塑化阶段。模具温度的分布和变化将影响熔体的流动阻力，因此冷却阶段的变化也可以体现在注射和保压阶段的控制曲线中。依据以上2点，试验的采样为注射和保压阶段的螺杆位移和压力曲线。试验采用900 kN伺服液压注塑机，螺杆位移通过光栅尺测量，压力采用液压系统压力，采样周期为3 ms。塑料材料为聚丙烯PPHT03，试验制品采用 68 mm×60 mm×41 mm的盒形件，平均壁厚为2 mm，以制品的成型质量作为评价指标。

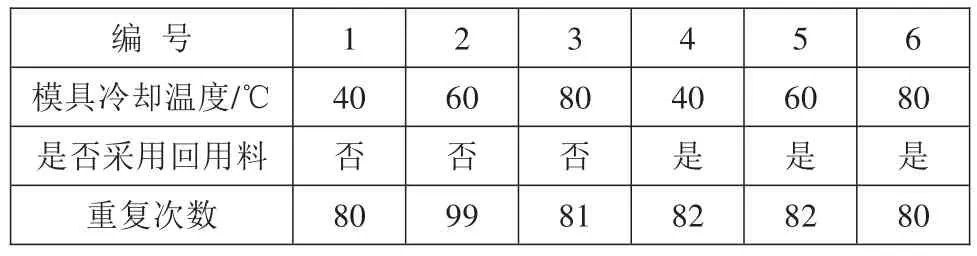
在实际注射过程中，即使考虑工艺参数不变，制品的成型质量也会由于环境或工况因素产生波动，设计了模具冷却温度和是否为回用料（制品经过回收粉碎后获得的原材料）作为工况变化的变量，并通过重复试验减少非控制变量对成型制品质量结果产生的影响，试验条件如表1所示。

故障监测模型采用均方差MSE和百分误差

%进行评价。MSE越小，表明模型分类越好，0表示没有误差。

%表明样本被错误分类的比例，0表示分类完全正确，100表示全部错误。质量预测模型采用MSE和回归系数

进行评价。

表示测量输出值和目标值之间的相关关系，

值为1表明相关性较高，0表示随机关系。

3 结果与讨论

3.1 故障监测结果与讨论

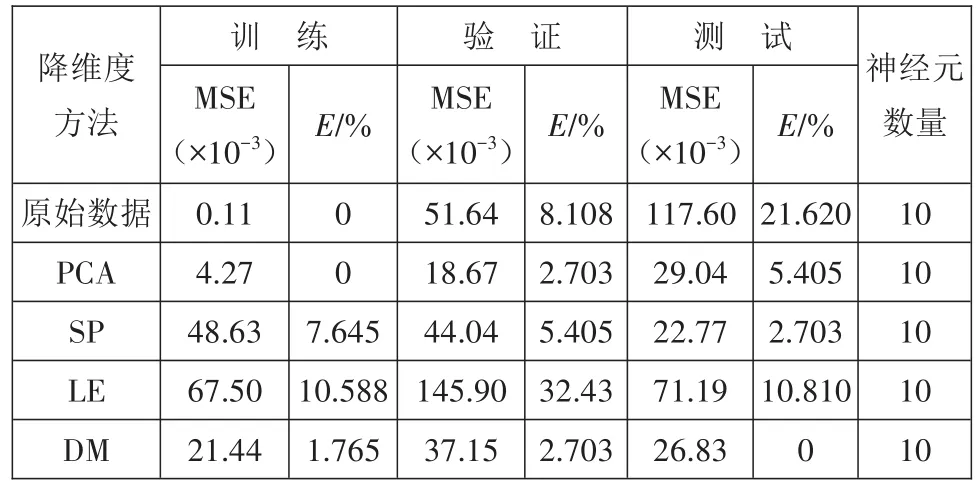
基于控制曲线判断制品原材料、模具温度是否属于正常类别，达到故障监测的目的。实际生产中，原材料虽然由加料处直接控制，但是原材料与回用料之间并没有严格的区分，容易造成混料，这样通过检测制品的生产过程曲线来判断原材料的种类以保证生产的正常进行很有必要。试验中采用原材料为1，回用料为0进行分类，试验结果如表2所示。

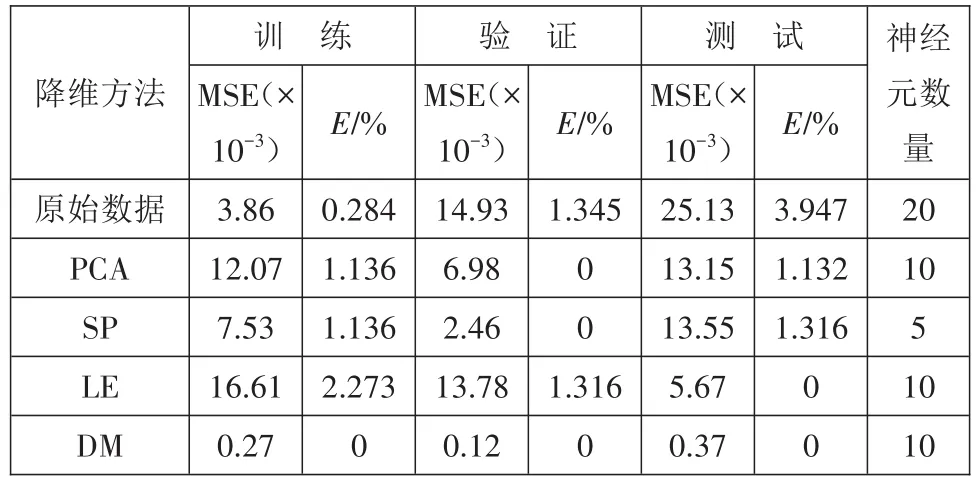
由表2可以看出：尽管相比于原始数据训练的均方差和百分误差，降维后的数据在验证集、测试集上都有较大的改善，LE和DM方法在测试集上百分误差为0。DM在训练、验证、测试时百分误差都为0，分类达到了100%正确。在神经元数量上，统计分析仅用5个隐层神经元，而原始数据却要使用20个，结合输入维度，统计分析18维，原始数据使用930维，仅输入层和隐层之间的前向计算就是930×20（计算输入值）+930（计算激活值），远大于统计分析的220（即20×10+20），增加了计算量，由此可以看出特征提取可以简化监测模型。

众所周知，机构各构件转角之间关系只取决于各构件相对长度。引入长度比例系数mb(称为凸轮偏心率)、ma和mc：

将模具温度40、60、80 ℃分别记为1、2、3类，不同降维度方法对应的分类结果如表3所示。相比于SP方法，原始数据在训练集、验证集和测试集上都比它们具有更小的均方差MSE和百分误差

%，这可能是因为SP方法仅保留了原始数据的统计特征，并没有提取与分类相关的直接有用的数据信息。PCA方法是一种基于全局的线性特征提取方法，相比于原始数据，PCA建模具有更好的泛化能力，即在训练集和验证集百分误差近似相等的情况下，在测试集上有更小的测试误差。LE和DM扩散系数图都是非线性降维度方法，其降维度获得的数据建立的模型更好。

3.2 质量预测结果与讨论

试验制品成型质量分布如图3所示，浅色线表示质量曲线，横线表示每个工艺状态下的平均质量，纵线区分不同的材料或模具温度，深色曲线表示所有样本的平均质量。由图3可知，由于工艺差异（模具温度）和材料状态不同（原材料和回用料），使成型制品质量整体波动剧烈，分布具有规律性，但难以直观地与螺杆位置、压力曲线建立关系。以均方差为标准，从训练集上看，原始数据的均方差最小，其次是DM、SP、LE，最后为PCA主成分分析法，表明使用原始数据训练的模型与训练数据匹配最好，同时这也与回归系数的结果一致。从验证集和测试集上看，与训练集相反，原始数据训练的模型在进行新的数据测试时回归系数仅为0.8，而一般使用降维度的数据所得到的回归系数为0.9，且均方差也小于原始数据模型，这表明由特征提取获得的数据更加具有代表性，将SP和DM方法获得的数据作为混合数据输入，从表4看出获得了更好的拟合效果。

治疗后，观察组和对照2组的临床治疗总有效率均显著高于对照1组，差异有统计学意义（P＜0.05）；观察组的临床治疗总有效率显著高于对照2组，差异有统计学意义（P＜0.05）。见表2。

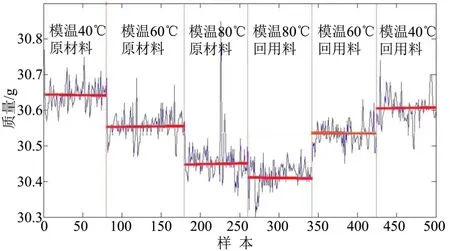
图4、图5所示是曲线原始数据与SP和DM方法降维后的混合数据在神经网络质量预测上回归系数的比较，其中

=

表示完全拟合，离此线越近，拟合效果越好。从图4、图5可知：原始数据在训练集上回归系数达到近0.99，但是在验证集、测试集上仅为0.77和0.81，造成这一现象的原因有2个：①数据过拟合，通过调整正则参数或神经元数量改进；②数据并没有代表性，即模型本身没有发现数据内在的关系。经过试验调整神经元数量，发现结果没有改进，说明原因由后者造成。经过SP和DM方法降维度后，制品质量的预测值不仅在训练集上，而且在验证集和测试集上都表现出较高的回归系数（>0.92），这表明采用SP和DM方法降维度后，提取了原始数据内在的高维度、非线性、强耦合的数据关系，摒弃了大量的冗余参数，提取的特征不仅使质量预测模型运行速度更快，而且提高了准确率。

4 结束语

基于采集的注塑机螺杆位置、压力信号，分析了主成分分析法、统计分析法、拉普拉斯映射法和扩散系数图法4种不同数据降维方法提取的特征，建立原材料、模具温度与制品成型质量之间的神经网络模型，进行注射成型过程的故障监测和质量预测，并设计试验进行了验证。试验结果表明，通过合适的数据降维方法，可以从螺杆位置与压力的信号中有效判断制品的原材料、模具温度是否正常，与未降维的数据和主成分分析法相比，拉普拉斯映射法和扩散系数图法等非线性降维方法可以解决成型过程曲线与制品质量的强非线性问题。同样应用在制品质量预测时，采用拉普拉斯映射法和扩散系数图法降维后，在验证集和测试集上都表现出高于0.92的回归系数，这表明拉普拉斯映射法和扩散系数图法提取了原始数据内在的高维度、非线性、强耦合的数据关系，摒弃了大量的冗余参数，使提取的特征用于质量预测模型时具有更好的精度和更高的效率，对发展基于成型过程传感曲线的高精度故障诊断和质量预测方法、提高塑料熔体注射成型过程的自动化程度具有重要意义。

[1]刘 阳.注塑制品质量参数在线检测、建模与优化方法研究[D].沈阳:东北大学,2010:8-9.

[2]周 俊,黄志高,周华民,等.注射模型腔压力监控系统的设计与实现[J].模具工业,2014,40(6):10-14.

[3]杨 洁.基于PCA的间歇过程监测及故障诊断方法研究[D].沈阳:东北大学,2010:5-49.

[4]李华伟,李 阳,郭 飞,等.注射模精密成型过程一致性在线监控方法研究[J].模具工业,2020,46(5):8-13.

[5]YI X H,XUAN F Z,LEEJAY,et al.Discriminant diffusion maps analysis:A robust manifold learner for dimensionality reduction and its applications in machine condition moni⁃toring and fault diagnosis[J].Mechanical Systems and Sig⁃nal Processing,2013,34(1-2):277-297.

[6]YUN Z,TING M,ZHI G H,et al.A statistical quality moni⁃toring method for plastic injection molding using machine built-in sensors[J].The International Journal of Advanced Manufacturing Technology,2016,85:2483-2494.

[7]马 莉,杜小荣.基于监督学习的核拉普拉斯特征映射的FCM算法[J].工业仪表与自动化装置,2016(4):9-12.

[8]倪家鹏,沈 韬,朱 艳,等.基于扩散映射的太赫兹光谱识别[J].光谱学与光谱分析,2017,37(8):2360-2364.

[9]王 军,冯孙铖,程 勇.深度学习的轻量化神经网络结构研究综述[J].计算机工程,2021,47(8):1-13.

[10]GUENTHERNICK,SCHONLAUMATTHIAS.Support vec⁃tor machines[J].The Stata Journal,2016,16(4):917-937.