基于改进DBSCAN的船舶轨迹聚类方法研究*

2022-03-17彭鹏菲

舰船电子工程 2022年12期

刘钰彭鹏菲

（海军工程大学电子工程学院武汉 430033）

1 引言

近年来，贸易全球化趋势日益强劲，海上运输已经成为贸易往来最重要的方式之一，随着海上船舶数量急剧增加，船舶交通现状日益复杂，与此同时也产生了大量的船舶航行轨迹，这给船舶交通管理部门的工作带来了不小的挑战，而研究这些船舶轨迹对全球海运的运输分析和监管具有重要意义。随着技术的不断发展，船舶自动识别系统（AIS）已成为全球海上实时交通信息重要来源［1］，根据AIS获取到的大量船舶特征信息来进行聚类分析，可以得到特定区域的船舶典型运动轨迹，对后续该区域的船舶进行轨迹预测打下基础，并且聚类效果越好，预测准确度也会越高，能够给船舶交通管理部门在海上运输安全和监管服务方面提供技术支持。

目前，国内外研究学者对船舶轨迹聚类进行了一系列研究。其中，利用AIS数据进行相关研究主要存在两种方式：基于轨迹点聚类以及基于轨迹段聚类。基于轨迹点的聚类主要以船舶位置（即经纬度）为特征来进行聚类簇的划分。Liu等［2］为了提取船舶航行的主轨迹，就是通过AIS数据对船舶轨迹点进行聚类。Yan等［3］通过对船舶轨迹点进行分类，从而得到船舶行为状态分别是在航和抛锚。基于轨迹点的聚类主要关注于船舶经纬度的变化，而对船舶相邻轨迹点之间的时空关联性缺乏考虑。基于轨迹段的聚类主要是将船舶的部分连续轨迹点作为整体来进行聚类，并且为了得到聚类簇，会对轨迹段进行相似度度量，因此，使用基于轨迹段的聚类方法来研究船舶轨迹特征会比基于轨迹点的聚类方法效果更好。LEE等［4］使用线性化的方式来处理轨迹段，通过最小描述长度距离选取特征点并进行相似度度量，从而获得了轨迹分布特征。魏照坤等［5～6］同样采用基于轨迹段的聚类方法实现了对船舶轨迹的线性化分。肖潇等［7］为了获得水域船舶的主要航路，通过选取船舶轨迹特征点划分轨迹段，并结合DBSCAN算法对轨迹段聚类。周海等［8］为研究船舶行为模式特征，采用融合距离（MD）来相似度度量船舶轨迹，但在船舶聚类特征的选取上只考虑了船舶轨迹的经纬度信息，忽略了同样能影响船舶航行的航向、航速等动态信息，并且使用的DBSCAN算法也只对船舶轨迹点进行聚类。

文献［9］可知研究船舶聚类的重要特征有船舶的经纬度、航向、航速等。因此，本文在对原始AIS数据进行预处理后，结合航向变化率和航速变化率获取特征点的方式来进行轨迹分段，充分考虑航向信息和航速信息后，采用融合距离（MD）进行船舶轨迹相似度度量，改进轨迹段的DBSCAN算法可以对轨迹分段后的轨迹子段进行聚类分析，通过实验分析，可以得到船舶典型运动轨迹，实验对比结果显示，本文所提聚类方法在一定程度上可以获得更好的聚类效果。

2 基于改进DBSCAN的船舶轨迹聚类模型构建

2.1 船舶轨迹聚类定义

船舶轨迹是指船舶在不同港口之间从事海上运输等任务时的航行轨迹。也就是说，船舶轨迹也就是一组轨迹的序列［10］。

船舶轨迹聚类是指将船舶航行轨迹按照相似度分成不同的类或簇，相似度高的轨迹归为同一簇，并且不同簇之间的轨迹特征差别较大。

2.2 船舶轨迹聚类的总体流程设计

通过比较现有文献可知，通过对船舶AIS数据的分析，可以提取轨迹的重要特征。采用轨迹聚类方法进行轨迹分析会遇到两类问题：轨迹相似度度量，以及选择适合的聚类算法。

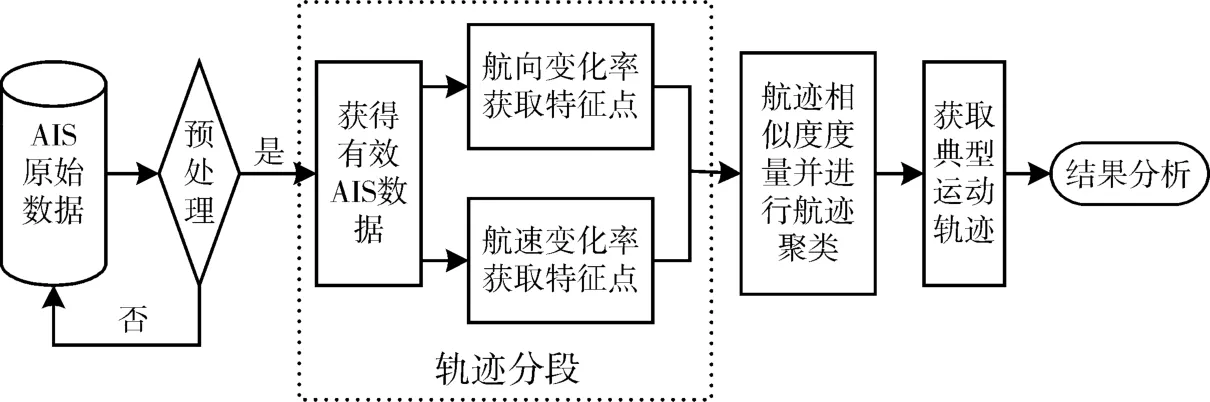
图1 基于AIS数据的船舶轨迹聚类流程图

2.2.1 AIS数据预处理

AIS数据包含了特定区域内的所有船舶的历史航行数据，而为了获得船舶的有序数据，需要人为地根据船舶MMSI以及采集时间进行筛选排序。

1）AIS数据清洗

数据清洗：删除各种异常数据，消除对后续轨迹建模的影响。

因此，需要删除船舶前后时间差较大的数据，拟合漂移数据，剔除噪声数据，对稀疏数据进行填补。

2）AIS数据缺失值处理

数据清洗后，容易存在前后两个轨迹点时间间隔较长的情况，为保证轨迹的完整性和精确性，需要对缺失值进行插补处理。

2.2.2 船舶轨迹分段

船舶轨迹分段是在原始航行轨迹中选取一些特征点，并且保证这些特征点之间的连线与原始轨迹尽可能地相似。在进行轨迹分段时，要尽量满足完整性和简洁性两个原则。

由船舶轨迹定义可知，大量船舶轨迹点组成了船舶轨迹，因此船舶轨迹序列可表示为

其中，pi表示船舶的第 i个轨迹点，pi={ti，loni，lati，sogi，cogi}，ti表示时间，loni表示经度，lati表示维度，sogi表示ti时刻的船舶航速，cogi表示ti时刻的船舶航向。

船舶轨迹示意图如图2所示。假设 p1-p9为某条船舶轨迹的数据采集点，船舶沿着p1-p9实线运动。如果将p1-p9全部作为船舶轨迹的特征点，虽然可以使船舶轨迹完整性更大程度的保留，但是会因为特征点选取过多，计算复杂，时间消耗大；如果只将 p1点、p5点、p9点作为特征点，虽然保证了较好的简洁性，但会丢失船舶原始轨迹的基本特征，不能保证轨迹的完整性。因此，最终选择 p1点、p4点、p6点、p8点作为特征点，这样得到的船舶轨迹 p1-p4-p6-p8能够同时保证完整性和简洁性。

图2 船舶轨迹划分实例

由图2可知，选择特征点对于进行船舶轨迹分段非常重要。根据文献［11］所提计算方法获取特征点，具体公式如下：

根据式（2），可以得到每个轨迹点的航向变化率和航速变化率，标记大于阈值的轨迹点，该类点即为特征点。

1）船舶航向信息度量

提前设定航向阈值来完成船舶航向信息的度量，由文献［12］可知，船舶航向转向角的定义：相邻船位连接的两个轨迹子段的航向差。在图3中，p3-p4和 p4-p5是两条轨迹子段，设定航向转向角阈值为θmax，将相邻船位船舶轨迹航向以及时间间隔代入式（2），就可以得到两条轨迹子段的航向变化率θ。将θ与θmax对比，如果θ≥θmax，则 p4点为特征点；如果θ＜θmax，就继续循环采样，直到遍历所有轨迹点。

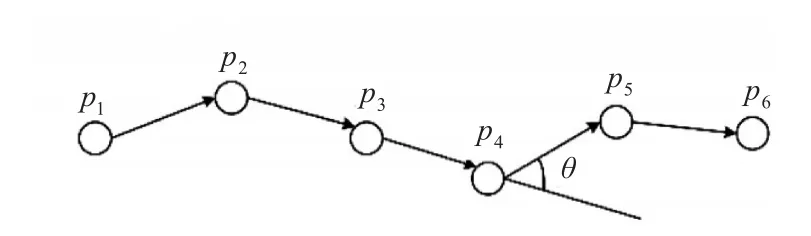
图3 船舶轨迹转向角

2）船舶航速信息度量

设 p4点的邻域距离为（dmin，dmax)，设定船舶航速阈值为vmax，假设 p4点的航速变化率为v，如果p4点的航速变化率与其他任意点的航速变化率的差的绝对值≥vmax，那么 p4点就叫变速点，也是需要被选定的特征点。如果p4点的航速变化率与其他任意点的航速变化率的差的绝对值＜vmax，那么继续采样，重复上述操作，直到遍历所有轨迹点。

通过上述两种信息度量方法可以确定特征点，连接相邻特征点，即可得到船舶轨迹子段。

2.2.3 船舶轨迹相似度度量

对船舶轨迹进行相似度度量是实现船舶轨迹聚类的基础，船舶动态信息是影响轨迹相似度度量的主要因素，例如经纬度、航向、航速等。因此，在实现船舶轨迹聚类时，将这些影响相似度度量的主要特征考虑在内，可以提高聚类效果。

针对不同的实际问题，运用不同的相似度度量方法会产生不同的聚类效果［13］。因此，需要根据船舶的特点来选择轨迹相似度度量方法。本文通过对航向和航速信息度量，从而对船舶轨迹进行相似度度量。假设船舶轨迹分段后的特征点表达式为T={p1，p2， ···，pn} 。

1）航向信息度量

由图4可知，Ta和Tb表示两条轨迹段；Pa1，Pb1和 Pa2，Pb2分别为轨迹段Ta，Tb的起点和终点；为Pa1，Pa2在Tb上的投影点，θ表示Ta和Tb之间的夹角。

图4 轨迹段距离计算示意图

Ta和 Tb之间的距离可表示为 d(Ta，Tb)=d∥+d⊥+dθ，其中 d∥表示水平距离，d⊥表示垂直距离，dθ表示角度距离，定义如下：

2）航速信息度量

文献［8］提出一种融合距离（the merge distance，MD）来进行轨迹段相似度度量，这种距离计算方法表示两轨迹段融合后的距离最短。图5为融合距离求最短轨迹段示意图。

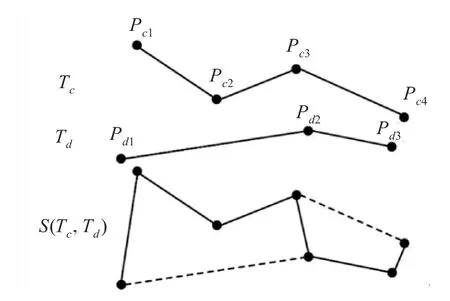
图5 融合距离求最短轨迹段示意图

如图5所示，Tc和Td表示两条轨迹段，Tc和Td分别由点序列 {pc1，pc2，···，pcm} ，{pd1，pd2，···，pdn} 构成，d(Pci，Pdj)表示两点之间的欧氏距离，其中1≤i≤m ，1≤j≤n，L(Tc)和 L(Td)分别表示轨迹段Tc和Td的长度；S(Tc，Td)表示轨迹段Tc和Td的最短超轨迹，用L(Tc，Td)表示其长度，即为最短超距离。

假设Tc[1 ， i]和Td[1 ， j] 分别为{pc1，pc2， ···，pci}和 {pd1，pd2，···，pdj}的超轨迹，用和表示，那么和中的最小值即为最短超距离L(Tc，Td)。

根据文献［8］，轨迹段Tc和Td之间的融合距离 MD(Tc，Td)表示为

一般情况下，融合距离MD(Tc，Td)会大于或等于 L(Tc)或者 L(Td)。将最短超距离 L(Tc，Td)除以L(Tc)与L(Td)和的平均值是为了进行归一化处理，此结果减1，MD(Tc，Td)的值也大于0。实际上，如果从同一轨迹上采样到轨迹段Tc和Td，那么两者的融合距离MD(Tc，Td)应接近于0，因为此时轨迹段Tc和Td的长度 L(Tc)、L(Td)和最短超距离L(Tc，Td)基本一致。因此，融合距离可以用在船舶轨迹相似度度量上。

2.2.4 改进轨迹段的DBSCAN算法

DBSCAN是一种最典型的基于密度的空间聚类算法［14］。该算法以划分簇的形式来聚类相似度高的轨迹，而簇的定义是密度相连的点的最大集合。因此，DBSCAN算法可以将数据密度足够的区域划分为簇，并且对噪声数据较为不敏感。

此前，研究人员大多使用DBSCAN算法对轨迹点进行聚类，而文献［4］、文献［15］、文献［16］、文献［17］则是利用改进轨迹段的DBSCAN算法进行聚类。基于改进轨迹段的DBSCAN算法的思想步骤：输入为所有轨迹段，并且将其全部标记为未聚类，读取某条轨迹段，然后根据ε邻域和minLns阈值来判断此轨迹段是否为核心轨迹段。如果是，则将此轨迹段标记为核心轨迹段，那么此核心轨迹段的ε邻域就形成了一个新簇C，然后将ε邻域内的所有点都加入簇C中，簇C通过ε邻域的核心轨迹段不断向外延伸判断，直到簇不再增长为止。基于轨迹段的DBSCAN算法的相关定义如下

定义1 Li邻域的公式化定义为

其中，ε表示轨迹段的密度半径；D为轨迹子段Li、Lj的数据空间，即 Li、Lj∈D ，与 Li的空间距离不超过ε的所有轨迹子段构成了Li的邻域。

定义2 对于Li∈D，Li为核心轨迹段的条件为：Li的邻域需满足

定义3 给定数据空间 D（Li∈D），Li为 Lj直接密度可达的条件为

其中，式（11）表示 Li在 Lj的 ε邻域范围内，式（12）表示Lj是核心轨迹段。

定义4 给定数据空间D（Li∈D），Ln为L1的密度可达的条件为：存在 L1，L2，L3，…，Li，…，Ln(1≤i≤n)，使得所有的 Li+1都是从 Li出发的关于ε和minLns的直接密度可达。

定义5 给定数据空间 D（Li，Lj∈D），Li和Lj是密度相连的条件为：存在任意轨迹段 Lk（Lk∈D），使得Li和Lj都是从Lk出发的关于ε和minLns的密度可达［18］。

图6是基于改进轨迹段的DBSCAN算法流程。

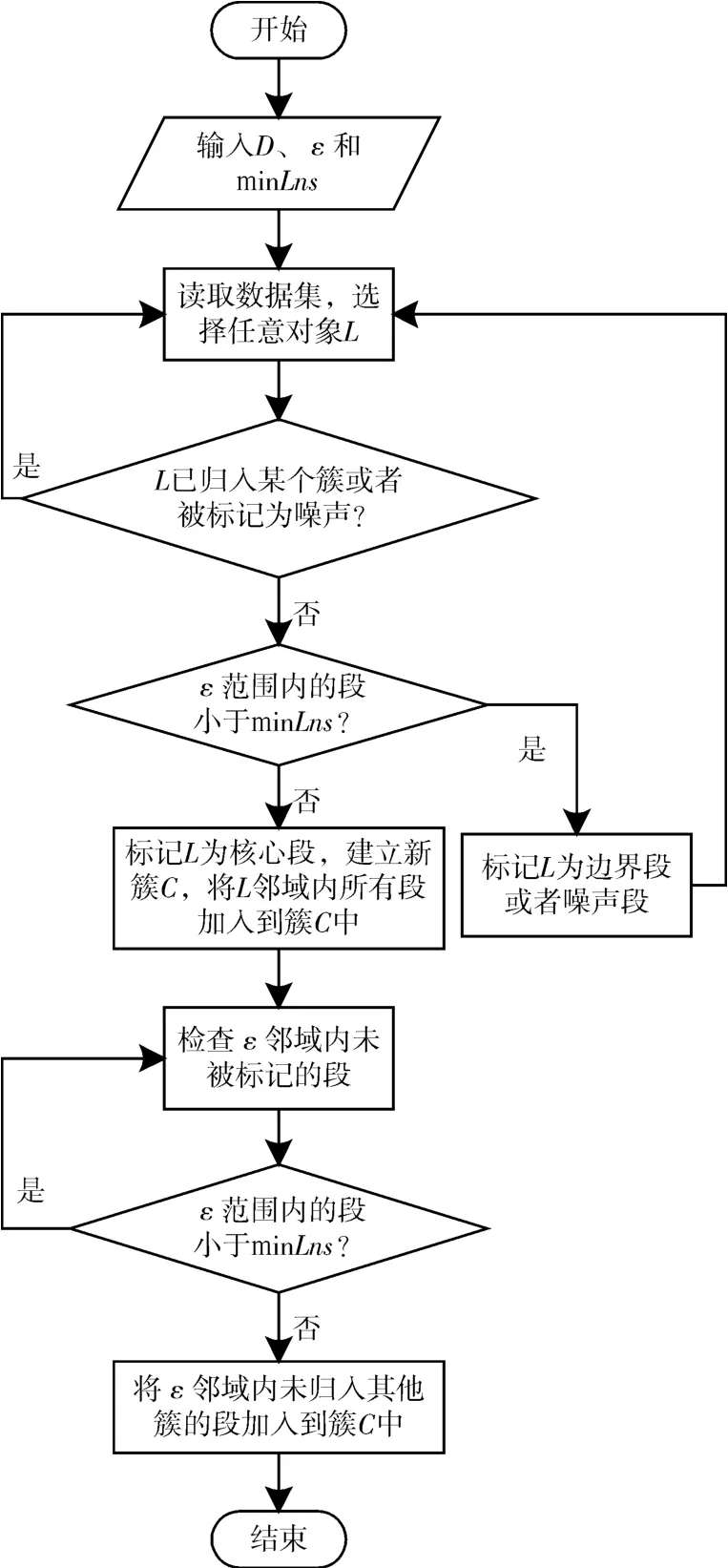
图6 基于改进轨迹段的DBSCAN算法流程图

经过上述算法流程可知，想要最终确定簇C，必须要遍历所有轨迹段。图7为核心轨迹段搜索区域示意图。从图中可知，搜索核心轨迹段的区域是一个半径为ε、密度阈值为minLns的外包椭圆，此时椭圆区域内的所有轨迹段构成了最终的簇。

图7 核心轨迹段搜索区域示意图

2.2.5 获取典型运动轨迹

为了获得船舶的典型运动轨迹，在经过改进DBSCAN算法划分轨迹段簇后，需要对每个簇中所包含的全部轨迹段的经度、纬度、航向和航速取平均值。

3 实验结果

本文从MarineCadastre.gov下载船舶的AIS数据，为了保证轨迹聚类的规律性，筛选出具有非对抗行为的商船和民船作为实验对象。因此下载了2019年8月27日至2019年8月28日在经纬度范围为（132.98E，34.01N）～（133.20E，34.16N）内的200条船的184998条轨迹数据进行聚类测试。

图8 测试海域范围示意图

根据航向信息和航速信息划分轨迹段后，得到了1564条轨迹子段，再利用本文方法对轨迹子段进行相似度度量和聚类。DBSCAN算法对ε和minLns的值比较敏感，并且ε和minLns参数值需要人为选择［19］。为了聚类效果更好，对于值的选取需要反复试验，经过多次试验，选定ε=0.003n mile，密度阈值minLns=7。根据此参数最后得到的船舶的典型运动轨迹如图9所示。

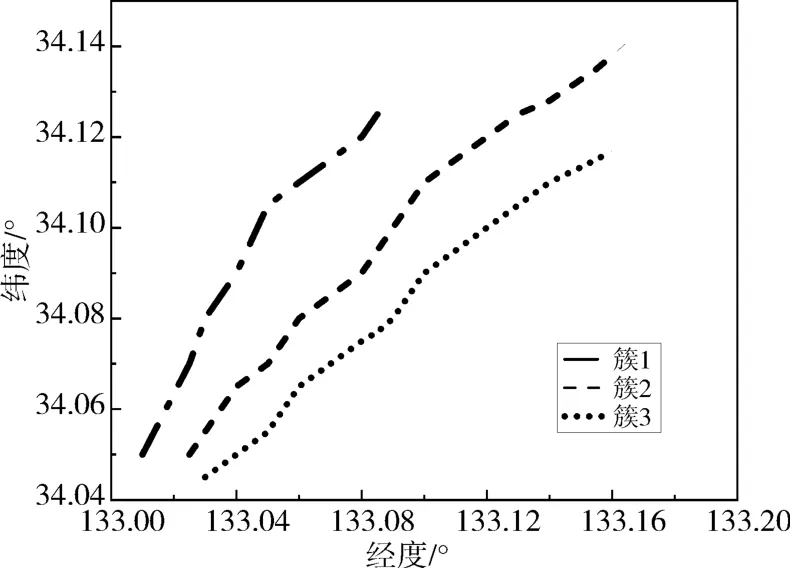
图9 船舶典型运动轨迹

在此范围内，经过聚类分析得到了3类簇。为了验证算法性能，采用紧密性（CP）这一无监督聚类指标来进行定量分析，定义如下：

其中，Ω为聚类后所形成的簇，K为聚类数量，wi为第i个簇。紧密性（CP）主要是计算每一个簇内各点到聚类中心的平均距离，CP值越低则表示簇内聚类的距离越近，那么聚类效果也越好。

将本文所用的融合距离（MD）与文献［10］所用的基于最长公共子序列（LCSS）、文献［20］所用的基于动态时间扭曲法（DTW）进行紧密性对比，结果如表1所示。

表1 三种算法紧密性结果对比

从实验结果可以看出，基于融合距离（MD）的相似度度量算法在聚类效果上比另外两种算法好，因为基于动态时间扭曲法（DTW）是通过压缩的方法，实现轨迹之间距离最小，并且对相似轨迹短时间内的个别差异非常敏感，无法准确衡量此类轨迹的相似度；基于最长公共子序列（LCSS）可以解决DTW方法存在的问题，但LCSS却把关注度放在了相似轨迹上，而忽略了不相似部分。因此采用基于融合距离（MD）的相似度度量轨迹段，可以有效地进行相似轨迹的归并与拟合，使得聚类结果更可靠。

为了更全面地体现本文算法的优势，将三种算法在聚类上所需时间进行对比，如表2所示。