基于单神经元PSD算法控制串级倒立摆系统

陈强，姚风麒，王国庆，金映波，李羽辰

（安徽工业大学，安徽马鞍山，243000）

关键字：串级倒立摆；单神经元；PSD控制算法

0 引言

本文针对常规PID无法有效控制倒立摆达到所需要求，设计了基于单神经元自适应PSD算法控制串级倒立摆，使得系统对非线性、自学习、自适应的处理能力得到加强，能够获得更好的控制品质。

1 系统数学建模

倒立摆是一种结构复杂的非线性系统，为了方便建模以及之后的数学推导，需要对系统进行如下假设:(1)摆杆为匀质刚体；(2)力矩电机的时间常数小，忽略电动机的空载转矩和系统摩擦，将电机、驱动器和机械传动装置视为纯比例环节，实测可得：Ks=1.6；（3）各子系统之间无相对滑动和摩擦，各种阻力和机械传动损失均忽略不计。根据图1倒立摆系统的物理模型。

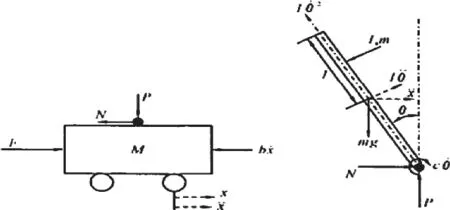
图1 倒立摆系统的物理模型

采用牛顿—欧拉法对倒立摆的小车和摆杆受力分析可得：

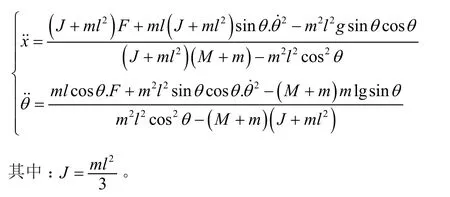
代入小车质量2kg，摆杆质量1kg，摆杆0.5m,重力加速度10m/s^2。则可以得直线一级倒立摆的简化模型为：

2 单神经元PlD控制算法原理

3 改进增益K的PSD控制算法

单神经元PID算法中的权系数和学习率根据不同的控制对象而选定，比例系数K值的选取对控制性能和动态稳定性的影响很大：K值小则对应的系统超调小，但上升时间会加大；反之，整个系统的快速性好，但超调大，调节时间会长；过大的K值，严重时则会导致系统的不稳定。改进K值的单神经元PSD控制结构图如下：

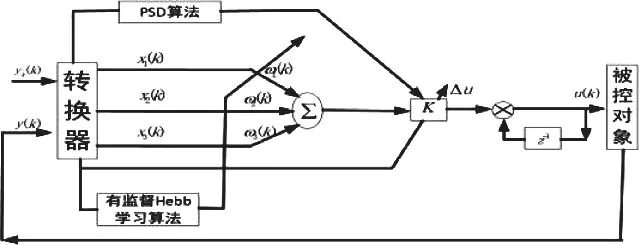
图2 单神经元PSD控制结构图

4 控制器设计

倒立摆系统的控制性能指标要求有：（1）响应时间小于5秒;（2）小车位移控制在平衡点不超过 ±5cm 处 ；（3）其摆杆角度在0.05rad以内。

倒立摆系统的控制目的：固定于导轨上的小车，在电动机的外力作用下，由于惯性使得摆杆能够维持竖直向上的稳定状态，与此同时小车能够限制在导轨区域内，即实现“摆杆不倒，小车停动”。而倒立摆系统的摆杆角度和小车位置利用传统PID无法同时进行调控。因而设计基于单神经元PSD算法控制的串级倒立摆方案，即内环副控回路采用常规PID系统控制器控制摆杆角度，外环主控回路利用单神经元PSD控制器固定小车位置。整个控制系统结构框图3如下。

图3 基于单神经元PSD的串级控制系统框图

内环未校正时的控制对象是非线性的自不稳定系统，设计内环控制采用典I型系统，即利用PD控制器进行反馈校正达到摆杆垂直向上的控制要求。

单神经元PSD控制器的设计是用s-function函数进行编写，该控制器是以误差变化量e(k)作为输入，经过延迟模块得到e(k- 1 ),e(k-2)。将s-function模块的输出u(k)，作为内部反馈给到模块输入，再经延迟模块有u(k-1)。其控制器通过对单神经元的加权系数和增益K值的调整来实现对外环的有效控制，权系数按照有监督的Hebb学习规则来调整，而比例增益K值则是根据无需辨识的自适应PSD控制算法来优化。

5 系统仿真

本文根据上述要求在MATLAB/Simulink中进行仿真实验，系统内环均采用PD控制其参数为：Kp=1.94，Kd=0.39。

图4为单神经元PSD控制串级倒立摆simulink仿真图，其中外环控制利用单神经元PSD算法编写s-function函数，初始化参数为：K_ 0 = 13，Tv_ 0 = 0.01，c=0.025，学习率η1=10；η2=0；η3=0.1，权值系数w1( 0) =Kp=0.1；w2(0) =Ki=0.1；w3(0) =Kd=0.1。图5中外环采用常规PID控制器代替单神经元PSD控制，其外环参数通过常规PID整定方法得到：Kp=0.045，Kd=0.09。

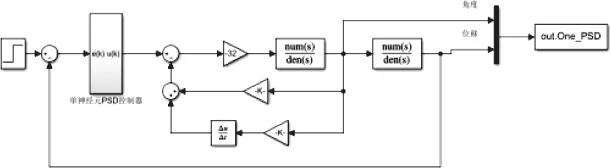
图4 单神经元PSD控制

图5 双闭环PID控制

在图6仿真结果表明所设计的单神经元PSD控制算法在串级倒立摆的控制中能够满足控制性能的基础指标。图7的对比表明，采用单神经元的PSD算法控制的串级倒立摆较之于传统PID算法在控制品质上，可以有效抑制其超调量，缩短达到稳态的时间，减少系统的输出振荡。

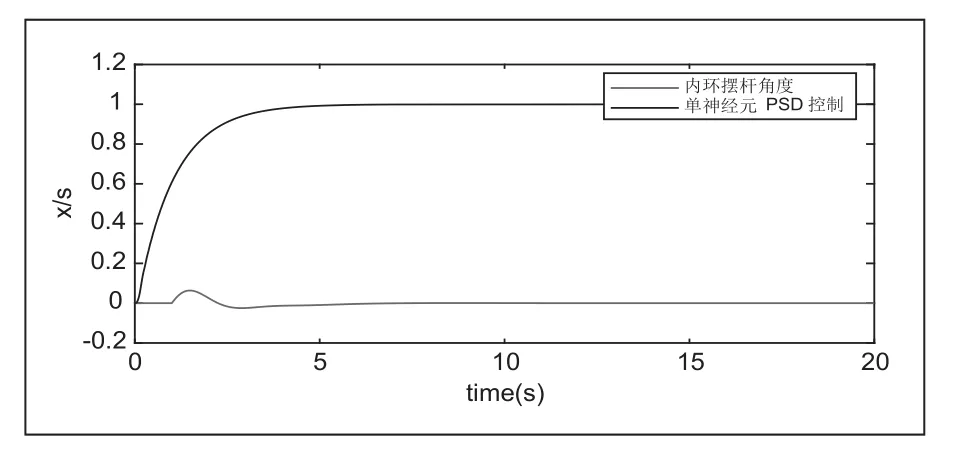
图6 基于单神经元PSD的系统阶跃响应仿真

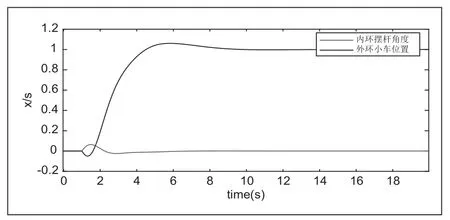
图7 基于常规PID的系统阶跃响应仿真

6 结论

本文通过对倒立摆模型的简化，进行模拟设计。利用传统PID算法设计的控制器无法快速有效的达到控制要求，在此基础上研究了结合单神经网络和优化神经元比例系数K的自适应PSD算法控制。系统的仿真结果表明，采用文中提出的控制方案，简化了系统的设计，有效减低了参数调整的复杂度，解决了传统PID控制和单神经元控制无法调节的K值的弊端。并且利用单神经PSD的特性不需要进行大量的网络训练，较之于完全的神经网络控制节省了时间，在工程运用中更能符合实际需求。