主动控制狭缝节流气浮支承结构及承载特性研究*

罗 强 于普良 胡 回 姜 庆 鲜小东

(1.武汉科技大学冶金装备及控制教育部重点实验室，机械传动与制造工程湖北省重点实验室，省部共建耐火材料与冶金国家重点实验室 湖北武汉 430081；2.武汉科技大学精密制造研究院 湖北武汉 430081)

静压气浮支承因其具有无摩擦和高运动精度的优点，已经广泛应用于各种精密设备中，如高精度导轨、光刻机和精密测量仪器等[1-2]。为了提高气浮支承的承载性能，通常使用的方法是改变气浮支承结构和采用控制技术。

于普良等[3]研究了不同截面均压槽对小孔节流气浮支承承载特性的影响，结果表明，通过增加均压槽可以提高气浮支承承载性能。CHEN等[4-5]研究了不同均压腔结构对小孔节流气浮支承承载性能的影响。龙威和宗洪锋[6]研究了环面、狭缝、小孔节流器对空气静压导轨的静态特性，结果表明狭缝节流效果优于其他2种。控制技术主要有被动控制和主动控制2种。在现有技术中，被动控制技术所提高的承载性能有限。相比之下，由于伺服控制系统的集成，主动控制方法表现出更高的承载性能[7]。ISHIBASHI、HUANG等[8-9]以小孔节流气浮支承为研究对象，从理论和实验两方面证明了主动调节节流面积可以提高支承的稳定性。AGUIRRE、AL-BENDER等[10-11]对气膜锥度控制进行了改进，利用压电促动器改变气膜锥度进而提高了承载性能。朱定玉、吴双[12-13]通过压电促动器控制气膜形状变化提高了气浮支承承载性能。MAAMARI等[14]通过线性弹簧控制气膜的锥度变化，并证明了气膜的圆锥度越大，产生的承载力越大。

目前许多主动控制的研究都是基于小孔节流方式，以控制气膜锥度变化为主，而对主动控制狭缝节流气浮支承的研究较少。本文作者设计了一种主动控制狭缝节流气浮支承，并建立计算流体动力学模型，通过Fluent仿真研究了径向狭缝高度变化幅值、径向狭缝高度、供气压力和气膜厚度对气浮支承承载性能的影响，为今后主动控制气浮支承的发展奠定了理论基础。

1 气体静压支承结构设计

1.1 工作原理

图1所示为可变节流面积静压气浮支承整体结构示意图。

如图1所示，气体从进气口进入，通过径向狭缝通道、轴向狭缝通道、均压腔流入气浮支承底部并通过出气口扩散开，从而起到支承作用。气浮支承开始工作时，压电陶瓷促动器受到电压激励后输出动态力，该动态力作用到柔性机构上，在力的作用下做微位移运动，进而导致伸缩机构下端面与气浮支承下端盖的上端面之间的径向狭缝高度Hb改变。径向狭缝沿中心展开后截面为长方形，气浮支承节流面积S=2π×D3×Hb，即改变径向狭缝高度可以改变狭缝节流面积。节流面积的改变直接影响了进入的气体质量流量，进而达到实现气浮支承承载力主动控制的目的。运动部分示意图如图2所示。

压电促动器上端与气浮支承上端盖螺栓连接，输出端顶在柔性结构上，伸缩结构与柔性结构螺栓连接，上端盖、柔性结构、下端盖三者通过螺栓连接。主要结构参数如表1所示。

表1 气浮支承主要结构参数

1.2 气体润滑数学模型

为了方便对气浮支承中的流动气体进行理论分析，建立以下假设条件：

(1)气体流动过程中流体的状态变化为等温过程，即温度T为常数。

(2)润滑气体的黏度系数η恒定。

(3)流体边界不考虑边界滑移效应。

(4)润滑气体满足理想气体状态方程。

基于以上假设，将N-S方程简化为一维流动分析，即：

(1)

对y积分2次，可得：

(2)

边界条件为y=0、z时，u=0，代入式(2)后可得：

(3)

式中：u为流体在x方向的速度；p为狭缝中的压力分布；μ为气体黏性系数。

压电促动器输出简谐力作用在柔性结构上，柔性结构在力的作用下做简谐运动。径向狭缝实际高度h为

h=hb+Δh

(4)

式中:Δh为扰动高度,

(5)

其中，ω为简谐运动频率；t为时间；A为运动幅值。

将式(5)代入到式(4)，此时径向狭缝气膜厚度：

h=hb+Δh=hb[1+ε·sin(ωt)]

(6)

综合径向狭缝扰动，可得径向狭缝内质量流量为

(7)

式中:b为径向狭缝周长；ρ为气体密度；R为气体常数；T为绝对温度。

整理得：

(8)

式中：pa为径向狭缝出口压力；h为径向狭缝高度；f为扰动频率。

设pb为轴向狭缝出口压力，pc为气膜对称中心压力。气膜向内部流动的质量流量为m1，向外流动的流量为m2，且Qm=m1+m2。

(9)

(10)

式中:hf为气膜厚度；ha为均压腔高度。将式(9)、(10)积分得到：

这个这个，当然能种。村长极力争辩。一条尺把宽的沟，充其量占你八斗丘的二十分之一，说不定更少，对你有什么影响呢。

(11)

(12)

式中：p1、p2为对应区间内任意一处压力，当r=r1时，p1=pb，当r=r2时，p2=p0，对其在区间内积分可得承载力公式：

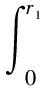
(13)

式中：s为气浮支承承载面面积。

由公式(8)、(13)可得，承载力与进口质量流量、径向狭缝高度、变化幅值有关。

1.3 主动控制狭缝节流气浮支承CFD模型

为研究气浮支承承载力的动态变化特性，文中利用计算流体力学软件三维动网格方法，用自定义函数控制径向狭缝上表面做正弦运动，模拟狭缝高度变化进行瞬态仿真分析。动态工况下狭缝变化如图3所示。由于空气静压支承的对称性，文中建立了1/4网格模型，所有网格为六面体网格，狭缝部分进行了网格加密处理。经过仿真验证，整体网格数量不少于200万时，计算结果保持稳定。CFD模型图如图4所示。

图5所示为主动控制狭缝节流气浮支承边界条件示意图，进气口压力为ps，出气口压力为标准大气压p0，气域模型两侧截面为对称边界，运动边界采用UDF控制，采用Dynamic Layering Methods网格更新方法，其他边界均设置为壁面。计算模型采用k-ε湍流模型，流动介质为理想气体。

1.4 仿真方法适用性验证

为了验证文中气浮支承CFD模型计算方法的可行性，利用参考文献[15]中气浮支承模型，使用文中湍流模型对该气浮支承进行了分析。文献[15]中气浮支承结构示意图如图6(a)所示，主要参数包括：气浮支承半径R2= 32.5 mm，狭缝深度H=10 mm，气膜厚度h=3～15 μm，狭缝宽度z=16 μm，狭缝所在圆半径R1=13 mm。气体为理想气体，气体流动为层流，速度-压力耦合算法为SIMPLE，供气压力ps=0.6 MPa，出口压力p0=0.1 MPa。

文中模型仿真结果与文献[15]中实验与仿真数据对比如图6(b)所示，3种方法结果具有一致性，验证了文中仿真方法在气浮支承计算仿真上的适用性。

2 仿真结果与分析

为研究进气狭缝节流面积动态变化对气浮支承承载力的影响，分析径向狭缝高度变化幅值、供气压力、径向狭缝高度和气膜厚度对气浮支承静态承载力、承载力变化范围的影响。径向狭缝高度变化方程为x=Asin(2πft)，f=1 000 Hz，Tp为0.001 s，每个周期迭代步数400步，时间步长为2.5×10-6s。

2.1 不同幅值、供气压力对支承承载力的影响

设置气浮支承CFD模型具体参数为径向狭缝高度Hb=5 mm，气膜厚度Hf=10 mm，径向狭缝高度变化频率f=1 000 Hz，变化幅值A分别为0.5、1、1.5、2、3 μm，供气压力ps分别为0.2、0.3、0.4、0.5、0.6 MPa，其他主要结构参数与表1相同，研究了不同变化幅值、不同供气压力时，气浮支承承载力W随时间t的变化。

图7所示为供气压力为0.6 MPa，径向狭缝高度变化幅值为2 μm时，气浮支承分别在时间t为1/4Tp、1/2Tp、3/4Tp、Tp时刻的压力云图。当径向狭缝处于正弦变化前1/2Tp时，径向狭缝高度Hb增加，气体质量流量增加，进而承载力增加，在t=1/4Tp时达到最大值；后1/2Tp时，承载力减小，当t=3/4Tp时，承载力最低。

图8所示为不同供气压力、不同径向狭缝高度变化幅值对承载力的影响。当供气压力ps为0.6 MPa时，随着径向狭缝高度变化幅值A的增加，狭缝节流面积S增加，进口质量流量增加，导致气膜内部压力分布增强，所以承载力变化范围逐渐增大。当保证变化幅值A不变时，如A=0.5 μm时，随着供气压力从0.2 MPa增加到0.6 MPa，静态承载力从220 N增加到310 N左右。可知，在变化幅值一定情况下，静态承载力和承载力变化范围随着压力的增大而增大；不同幅值时在各压力条件下，整体承载力变化趋势相似，呈周期性变化。当0

2.2 不同幅值、径向狭缝高度对支承承载力的影响

设置气浮支承CFD模型具体参数为气膜厚度Hf=10 mm，供气压力ps=0.6 MPa，径向狭缝高度变化频率f=1 000 Hz，径向狭缝高度Hb分别为4、5、6、8、10 μm，径向狭缝高度变化幅值A分别为0.5、1、1.5、2、3 μm，气浮支承其他主要结构参数与表1相同，研究了气浮支承底面承载力W随时间t的变化。

如图9所示，当径向高度一定时，随着狭缝高度变化幅值A的增加，质量流量增大，压力分布增强，承载力变化范围逐渐增大。当保证变化幅值A不变时，随着径向狭缝高度的增大，静态承载力增加幅度较小，承载力变化范围减小。当径向狭缝高度为10 μm时，随着时间变化，承载力几乎不变，范围最小只有2 N左右。承载力随时间变化的范围随着变化幅值的增大而增大,随着径向狭缝高度的增大而减小，变化规律呈周期性变化。在Hb=4 μm，A=3 mm时，承载力最大范围达到了130 N。

2.3 不同幅值、气膜厚度对支承承载力的影响

设置CFD模型具体参数为径向狭缝高度Hb=5 μm，供气压力ps=0.6 MPa，径向狭缝高度运动频率f=1 000 Hz，气膜厚度Hf分别为5、10、15、20、25 μm，径向狭缝高度运动幅值A分别为0.5、1、1.5、2、3 μm，气浮支承其他主要结构参数与表1相同，研究了不同变化幅值A、不同气膜厚度Hf时，气浮支承承载力W随时间t的变化。

如图10所示，当气膜厚度一定时，随着径向狭缝变化幅值A的增加，承载力变化范围同样增大，承载力均呈周期性变化。当运动幅值不变时，随着气膜厚度Hf的减小，静态承载力和变化范围都在增大，当气膜厚度减小到5 μm时，静态承载力虽然增大但变化范围缩小。承载力变化范围随着运动幅值的增大而增大，随着气膜厚度的增大而减小。

3 结论

(1)通过可变节流面积狭缝节流气浮支承的仿真分析，结果表明主动控制节流面积可以实现气浮支承承载力的动态调节，为主动控制气浮支承的研究奠定了理论基础。

(2)当主动控制节流面积气浮支承的其他参数不变时，保持径向狭缝高度变化幅值一定，增大供气压力，静态承载力及变化范围都大幅度增加；供气压力一定时，承载力变化范围随着变化幅值的增大而增大。

(3)当主动控制节流面积气浮支承的其他参数不变时，保持径向狭缝高度变化幅值一定，增大径向狭缝高度，静态承载力增加，但变化范围减小；径向狭缝高度一定时，承载力变化范围同样随着变化幅值的增大而增大。

(4)当主动控制节流面积气浮支承的其他参数不变时，保持径向狭缝高度变化幅值一定，增大气膜厚度，静态承载力大幅度降低，但变化范围先增大后减小;气膜厚度一定时，承载力变化范围同样随着变化幅值的增大而增大。