一种相变储热器内翅片结构的快速优化算法

蔡肖，徐阳，杨超，郑章靖

（中国矿业大学电气与动力工程学院，江苏省 徐州市 221116）

0 引言

通过添加翅片改善管壳式相变储热器性能的研究可以追溯到几十年前。早期关于相变储热单元内翅片的实验和理论研究主要集中在纵向和径向翅片上。通过一系列实验以及数值模拟研究，研究人员发现相比于径向翅片，纵向翅片对管壳式相变储热器的强化效率要高一些。传统的纵向翅片是指扁平翅片，其横截面积不随翅片的高度变化。然而，管壳式相变储热器的横截面积沿其半径逐渐变化。也就是说，传统的纵向翅片并不是改善管壳式相变储热器熔化和凝固性能的最佳选择。因此，需要对纵向翅片进行进一步的改善。

由于传热传质的相似性，Y 形翅片已被广泛用于提高管壳式相变储热器的熔化和凝固性能。Zhao 等人[9]比较了一级Y 形翅片和纵向翅片对熔化与凝固过程的影响，数值模拟结果显示，与纵向翅片相比，一级Y 形翅片可分别减少70%和81%的熔化和凝固时间。Yu 等人[10]以相变储热单元的最小完全熔化时间作为优化目标，对用于增强管壳式相变储热器熔化性能的Y 形树状翅片进行了结构优化，研究结果表明，优化后的翅片结构可以使储热器的完全熔化时间缩短26.7%。Zhang 等人[11]以最小完全凝固时间作为优化目标，对水平管壳式相变储热器内的2 级Y 形翅片进行了优化研究，结果表明，优化后的翅片结构可以使储热器的完全凝固时间缩短66.2%。

上述研究表明，通过对翅片进行优化可以显著提高相变储热单元的熔化或凝固效率。然而很多目标函数需要在完全熔化或凝固的基础上得出，通过数值模拟对储热器的熔化或凝固过程进行研究需要消耗大量的时间，优化进度较慢。因此本文以翅片均匀布置为指导原则，提出以相变材料到翅片和冷源的距离最短为优化目标，并通过遗传算法对管壳式相变储热器内的一级Y 形翅片进行结构优化。通过对比优化前后2 种翅片结构的管壳式相变储热器的凝固过程，对优化目标的可行性进行验证。

1 物理模型

本文选取水平放置的管壳式相变储热器作为研究对象。该储热器由内管、外管、相变材料以及Y 形翅片组成。由于水平放置的管壳式相变储热器的轴向温度梯度远小于径向温度梯度，因此将凝固过程的相变储热单元简化为二维的相变储热单元，如图1 所示。此外，自然对流在凝固过程中很弱，传热以热传导为主[12]。因此，忽略自然对流，选择图1中模型的1/2作为计算域(见图1中的虚线区域）。忽略壁厚的影响，内管的半径Ri为10 mm，外管的半径Ro为20 mm。为了便于优化分析，对Y 形翅片的各分支长度(l0，l1)、各分支宽度(w0，w1)以及一级分支的夹角(θ)进行无量纲化处理。无量纲翅片各分支长度(L0，L1)、厚度(W0，W1)以及一级分支的夹角(η)的定义如式(1)所示：

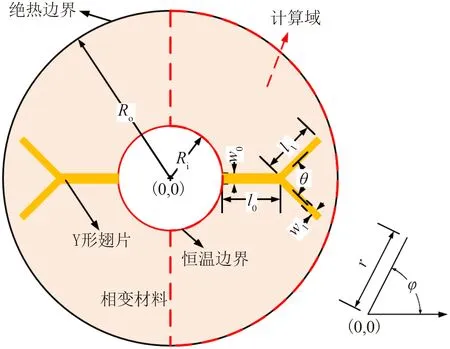
图1 物理模型Fig.1 Physical model

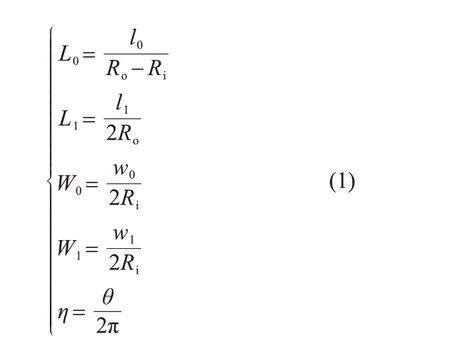
同时利用翅片的分支宽度比δ对翅片各分支的宽度关系进行表示，如式(2)所示：

研究中，翅片的占比始终保持在10%。为了强化换热，翅片为铜材质制作而成，选用石蜡作为相变材料。石蜡和铜的物性参数见参考文献[13]。

两组患儿治疗后临床疗效比较 见表1。两组患儿治疗后临床疗效比较,治疗组痊愈率和总有效率均有明显提高,差异具有统计学意义。

2 数学模型

2.1 控制方程

如图1 所示，模拟区域包括翅片区域和相变材料区域。在相变材料区域，焓-孔隙率模型用于描述固-液相变过程。因为自然对流的影响被忽略，所以相变材料区域的控制方程仅包括能量方程。相变材料区域以及翅片区域的能量方程参考文献[14]。

2.2 初始条件及边界条件

如图1所示，所涉及的边界条件包括：1）内管壁为恒温边界，其温度为300 K，即Tin=300 K；2）外管为绝热边界，即q=λ∂T/∂r=0，其中q，λ，r分别为热量、导热系数和极径坐标。

管壳式相变储热器的初始条件为：相变材料与金属翅片具有相同的温度，初始温度为321.66 K。

2.3 数值方法与验证

数值模拟过程中计算域如图1虚线区域所示。整个计算域用四边形的结构化网格来划分。采用有限体积法求解计算域内的能量方程。能量方程中的扩散项采用二阶迎风格式进行离散。能量方程的收敛标准设定为10-6。

为了确保数值计算的准确性，进行了网格无关性验证。此外，为了进一步减小数值结果的误差，还进行了时间步长τ独立性测试。本节采用了装有一个Y 形翅片的相变储热单元进行网格无关性和时间步长独立性试验。翅片无量纲参数为：L0=0.5，W0=0.04，L1=0.1，W1=0.08。选取网格尺寸分别为0.05，0.1，0.2，0.5，1 mm的5种网格系统作为研究对象，时间步长为0.1 s。图2为5种网格系统的完全凝固时间ttotal。结果表明，相对于尺寸为0.05 mm 的网格系统，尺寸为0.1 mm 的网格系统的完全凝固时间缩短了0.04%。因此，在综合衡量计算精度与计算时长的情况下，本文选取了尺寸为0.1 mm的网格系统。另外，在网格无关性验证的基础上，分别研究了0.05，0.1，0.2，0.5 和1 s 五种不同时间步长对数值模拟结果的影响。5 种不同时间步长对应的液相分数随时间的变化情况如图3所示。从图3中可以看出，当时间步长为0.05 s 时，液相分数的动态变化情况与时间步长为0.1 s时的变化情况一致。因此，本文选取的时间步长为0.1 s。

图2 网格无关性验证Fig.2 Grid independence verification

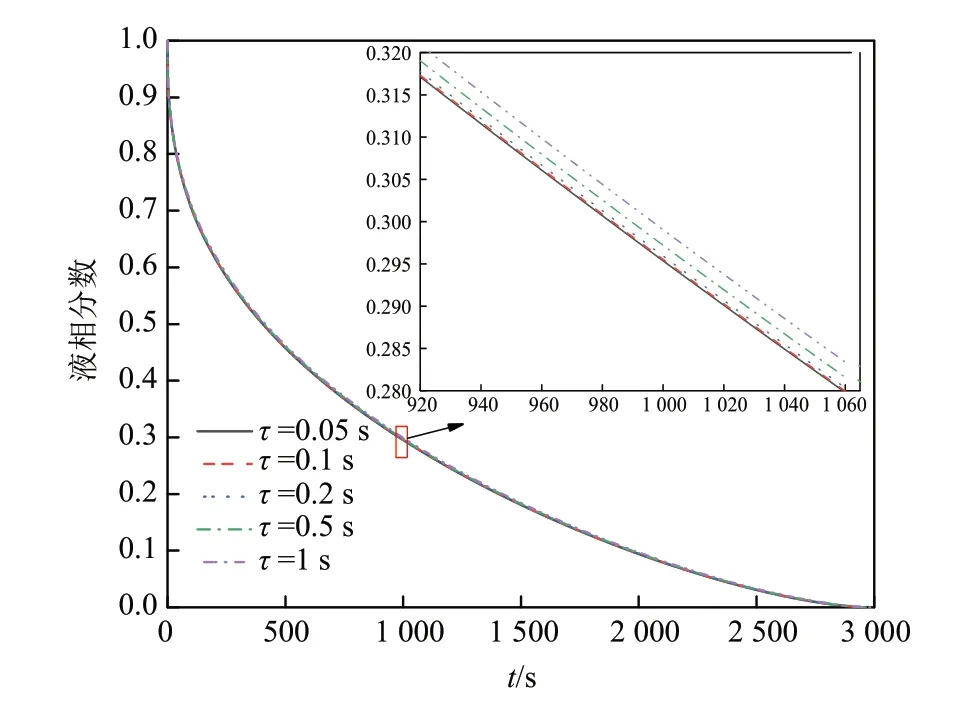
图3 时间步长独立性验证Fig.3 Time step independence verification

2.4 模型验证

通过与Ismail等人[15]的实验结果对比，验证当前所使用数学模型的可靠性。该实验研究了4个纵向翅片对管壳式相变储热单元中凝固过程的强化作用。数值模拟中，相变储热单元的结构参数与文献[15]中保持一致。系统的初始温度为338.15 K，内管壁面温度维持在313.15 K。选用商业石蜡作为相变材料，其物理性质见参考文献[15]。图4 显示了数值模拟与实验所得的凝固前沿，其中X、Y分别为水平和垂直方向翅片长度。从图4 可以看出，本文所采用的数值模型的计算结果与实验结果具有较好的一致性，验证了在翅片强化作用下，本文所采用的数值模型具有一定的可靠性。

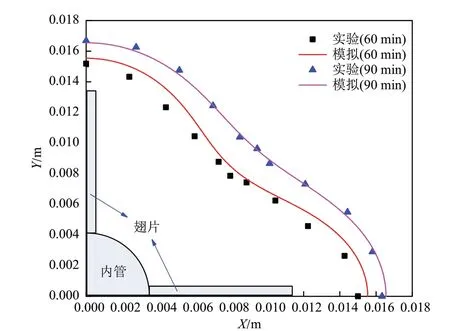
图4 模型验证结果Fig.4 Model verification results

3 优化算法

为了解决传统优化过程耗时长的问题，本文以翅片均匀布置为指导原则，提出以相变材料到翅片和冷源的距离最短为优化目标。首先通过对计算域进行离散化处理，将其划分为大小相同的网格，如图5 所示。然后通过网格中心点坐标，判断网格是否属于翅片区域，并分别记录翅片区域与相变材料区域的网格中心点坐标分别记录。选取相变材料区域网格点Pn(n的取值范围为1～m，m为相变材料区域网格数量)，其中心点坐标为(xPn，yPn)，通过逐一求取该网格点到翅片区域网格点(xQ,fin，yQ,fin)的距离，选取其中的最小距离即为相变材料网格点Pn到翅片最小距离dPn_fin，由式(3)计算得出。然后求取相变材料区域网格点Pn到冷源(内管)的距离dPn_wall，由式(4)计算得出。通过对比dPn_fin和dPn_wall，选取距离最小值dmin_Pn，如式(5)所示。dmin_Pn即为相变材料区域网格点Pn到冷源和翅片的最小距离。在不考虑相变材料到冷源的距离时，式(5)中的dmin_Pn为相变材料区域网格点Pn到翅片区域网格点的最小距离dPn_fin。以图5 中相变材料区域网格点P1为例，P1点到冷源(内管)的距离为dP1_wall，翅片区域到P1 点距离最短的网格点为P1′网格点，其距离为dP1_fin。通过对比dP1_wall与dP1_fin，选取距离最小值。同样的方法可以得到dmin_P2与dmin_Pn。通过逐一调取相变材料区域网格点，可以得到相变材料区域内各个网格点到冷源(内管)和翅片的最小距离。将所有相变材料区域网格点到冷源(内管)和翅片的最小距离求和，即得到相变材料到翅片和冷源(内管)的距离dsum，如式(6)所示。

图5 最小距离计算示意图Fig.5 Schematic diagram of minimum distance calculation

选取Y 形翅片的各分支无量纲长度、宽度比以及分支无量纲夹角为设计变量。翅片无量纲参数的变化范围均为0～1。因此，本文的优化问题有4个设计变量。优化问题可表述如下：

目标函数：F=min(dsum)。

设计变量：L0=0～1，L1=0～1，δ=0～1，η=0～1。

基于达尔文进化理论的遗传算法因具有全局搜索特性、对梯度信息的不依赖性和易于操作性，近年来被广泛应用于解决多类组合优化问题[16]，故本文将遗传算法引用到相变储热器中的翅片优化研究中。遗传算法与前处理模块、数据处理模块相耦合的流程如图6 所示。优化过程的主要步骤如下：1）首先通过前处理模块，生成计算域网格，并将每个网格的中心点坐标输出，存储到共享文件1；2）通过遗传算法生成初始种群，并将个体变量输入到共享文件2中；3）利用数据处理模块读取共享文件1与共享文件2中的数据。利用共享文件2中的翅片参数判断共享文件1中的网格是否在翅片区域内，通过计算得到相变材料到翅片和冷源(内管)的距离，并将计算结果输入到共享文件3 中；4）遗传算法从共享文件3 中读取适应值，并对其进行适应度值评估。若满足终止准则，则输出最佳变量；若不满足，则通过一系列杂交、变异产生新的种群，进而重复执行适应度值计算以及评估，直至满足终止准则[17]。

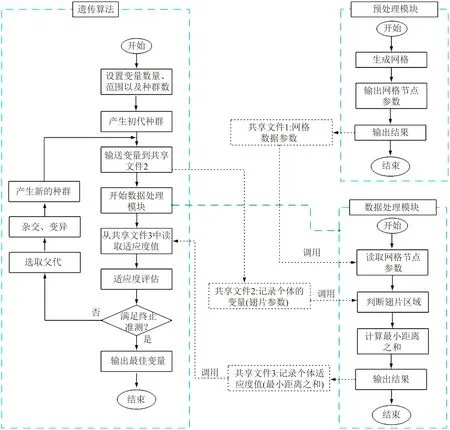
图6 优化程序流程图Fig.6 Optimization program flow chart

4 结果与讨论

4.1 单翅片优化结果

遗传算法的种群数量在很大程度上影响算法的收敛速度和解的质量。种群数越小，算法收敛越快，但会导致解的精度不足；种群数越大，求解精度越高，但耗时越长。因此，首先研究种群数对于优化结果的影响。选择单个Y 形翅片的无量纲夹角η作为优化变量，其变化范围为0～1。各分支的无量纲长度L0，L1分别为0.5 和0.1，分支的宽度比δ为1。在优化过程中，通过改变翅片各分支的宽度来保证翅片的占比不变。本文研究了3种不同的种群数量(10、20和40)对于求解速度以及优化结果的影响，图7显示了3个种群数量下优化过程中产生的不同η及其对应的适应度值，其中适应度值为相变材料到翅片和冷源(内管)的距离dsum。从图7 中可以看出，随着种群数的增加，遗传算法产生了更多的个体，种群数量为10、20和40 时产生的个体数量分别为15、36 以及44，更多的个体意味着更有可能找到最优的结果。但是，种群数量的增加也意味着优化所需的时间增加。当种群数为10时，最优个体为η=0.375，其适应度值为dsum= 195.373 7。当种群数为20 时，最优个体为η= 0.395，其适应度值为dsum=195.150 6。当种群数为40 时，最优个体为η=0.395，其适应度值为dsum=195.089 9。可以发现，当种群数由10增到20时，最佳个体的适应度值有所下降。但是，当种群数继续增加到40时，优化获得的最优个体与种群数为20时获得的最佳个体相同。因此，在综合衡量优化精度以及优化耗时的情况下，在后续的研究中均设置种群数为20。

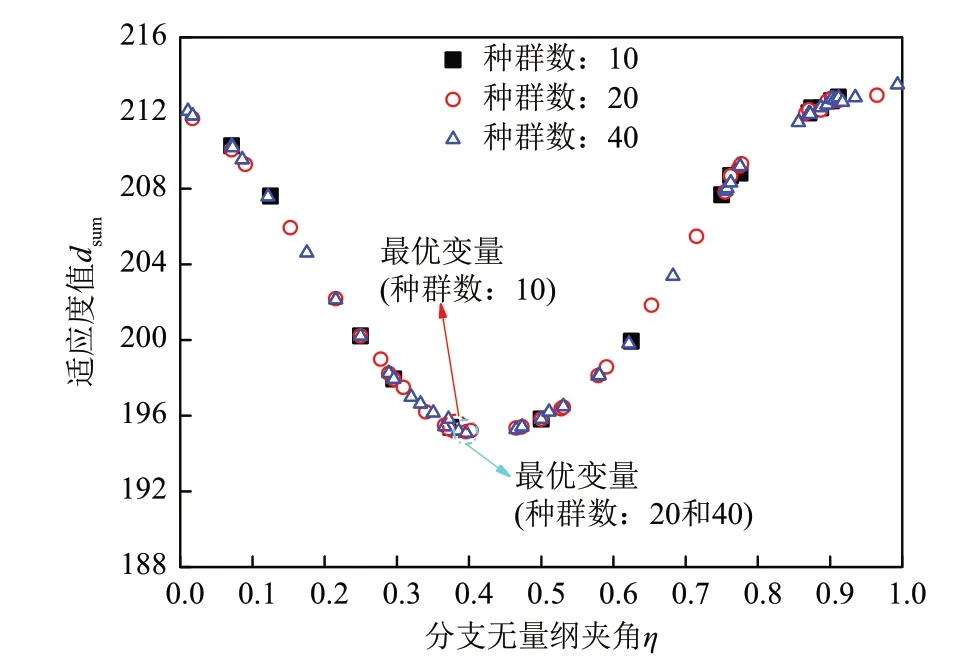
图7 单翅片分支夹角作为变量的优化结果Fig.7 Optimization results of single-fin branch angle as a variable

是否考虑冷源对翅片最优结构的设计有着重要的影响。因此，本节选取单个Y 形翅片的各分支无量纲长度L0、L1，翅片宽度比δ以及无量纲夹角η作为变量，研究了是否考虑相变材料到冷源(内壁)的距离对优化结果的影响。2种约束条件下优化所得的翅片结构参数如表1 所示。其中：case0表示未考虑相变材料到冷源距离时优化所得的翅片结构；case1表示考虑相变材料到冷源距离时优化所得的翅片结构。图8为2种约束条件下优化所得的翅片结构示意图，可以看出，优化后的翅片结构呈现箭头形。case1 得到的翅片比case0得到的翅片的分支之间的夹角要小。

表1 优化后翅片结构参数Tab.1 The optimized fin structure parameters

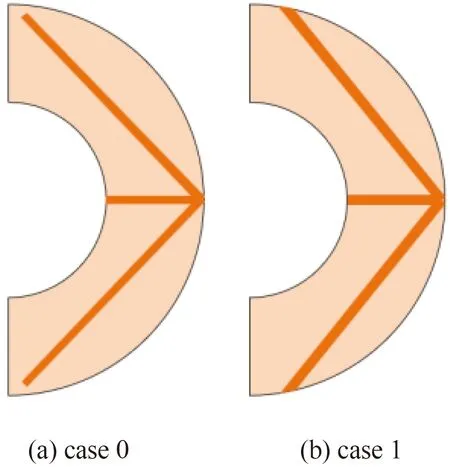
图8 2种约束条件下优化所得的翅片结构示意图Fig.8 Schematic diagram of fin structure optimized under two constraints

图9为2种优化条件下所得的翅片对凝固过程的影响，可以看出，在凝固过程前期，2 种结构的凝固速率基本一致；随着凝固过程的进行，case1 具有更好的强化性能，相比于case0，case1可以使完全凝固时间缩短24.99%。这是因为case1得到的翅片的各分支宽度大于case0。而随着翅片宽度的增加，翅片的传热效率有所增强，从而加快了储热器的凝固速率。图10 为2 种翅片结构下不同时间的液相与温度分布云图，可以看出，在凝固中后期，由于case1更加靠近外管壁面，能够缓解凝固中后期case0在外管附近造成的传热滞后区问题，从而使得储热器的凝固速率得到提高。因此，在翅片优化过程中，考虑相变材料到内壁距离可以更好地强化翅片结构性能。

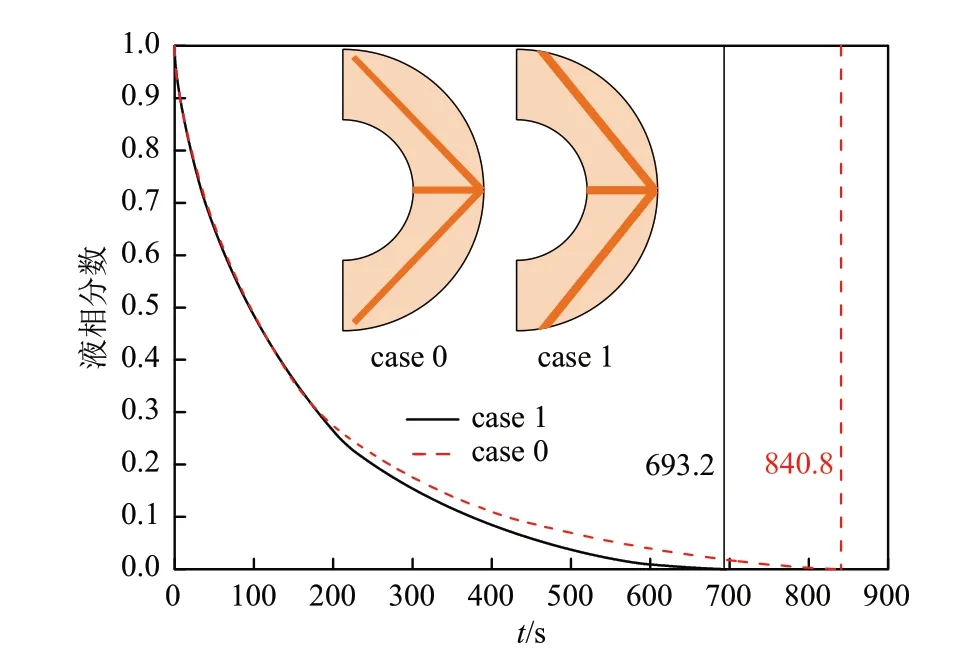
图9 2种优化条件下所得翅片对凝固过程的影响Fig.9 Effects of fins on solidification process under two optimized conditions

图10 2种翅片结构下不同时间的液相与温度分布云图Fig.10 Cloud images of liquid phase and temperature distributions at different times under two kinds of fin structures

通过对比传统Y 形翅片和箭头形翅片储热器内相变材料到翅片和冷源的距离以及完全凝固时间，来进一步说明优化目标的可行性。选取分支无量纲夹角为0.167、0.25、0.333、0.417、0.5，以及主翅的无量纲长度为0、0.1、0.3的传统Y形翅片进行对比研究。图11显示了不同结构的翅片储热器内相变材料到翅片和冷源的距离。从图中可以看出，优化后的箭头形翅片储热器内相变材料到翅片和冷源(内管)的距离最短。图12 显示了不同翅片储热器的完全凝固时间，可以看出，通过优化得到的箭头形翅片结构具有更好的强化效果。相比于传统Y 形翅片，箭头形翅片结构可以使完全凝固时间最少缩短62.1%。对比图11 与图12可以看出，虽然个别算例中距离与完全凝固时间具有一定的误差，但利用本文提出的以相变材料到翅片和冷源距离最短作为优化目标获得的新型结构具有一定的优越性。因此，该优化目标可以较好地对翅片结构进行优化。

图11 不同结构的翅片管壳式相变储热器内相变材料到翅片和冷源的距离Fig.11 Distance between phase change material and fin and cold source in different finned shell and tube phase change heat storage

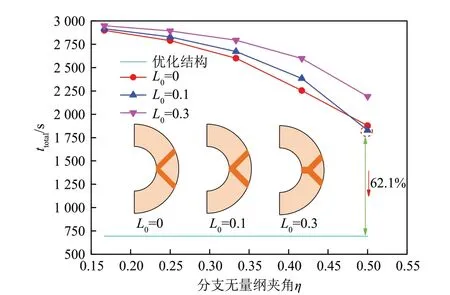
图12 不同结构参数的翅片管壳式相变储热器的完全凝固时间Fig.12 Complete solidification time of finned shell and tube phase change heat storage with different structural parameters

4.2 多翅片优化结果

Y 形翅片的数量N直接决定了管壳式相变储热单元中翅片的空间布局，对相变材料的能量释放性能起着重要作用。选取数量为2和3的翅片结构进行优化研究。鉴于翅片是均匀分布设计，每个翅片具有相同的参数，因此优化变量的数量不随翅片数量而变化，即优化变量始终为：分支无量纲长度L0、L1，翅片宽度比δ以及无量纲夹角η。表2 显示了在不同翅片数量下优化所得的翅片结构参数，可以看出，翅片数量变化的同时，优化后的翅片结构参数也会发生改变。当翅片数量从2增加到3时，单个翅片的第0级分支的宽度减少了37.2%，第1 级分支的宽度减少了67.5%。优化后的翅片结构示意如图13所示，可以看出，对于多数量的翅片，优化后的翅片仍呈现箭头形。

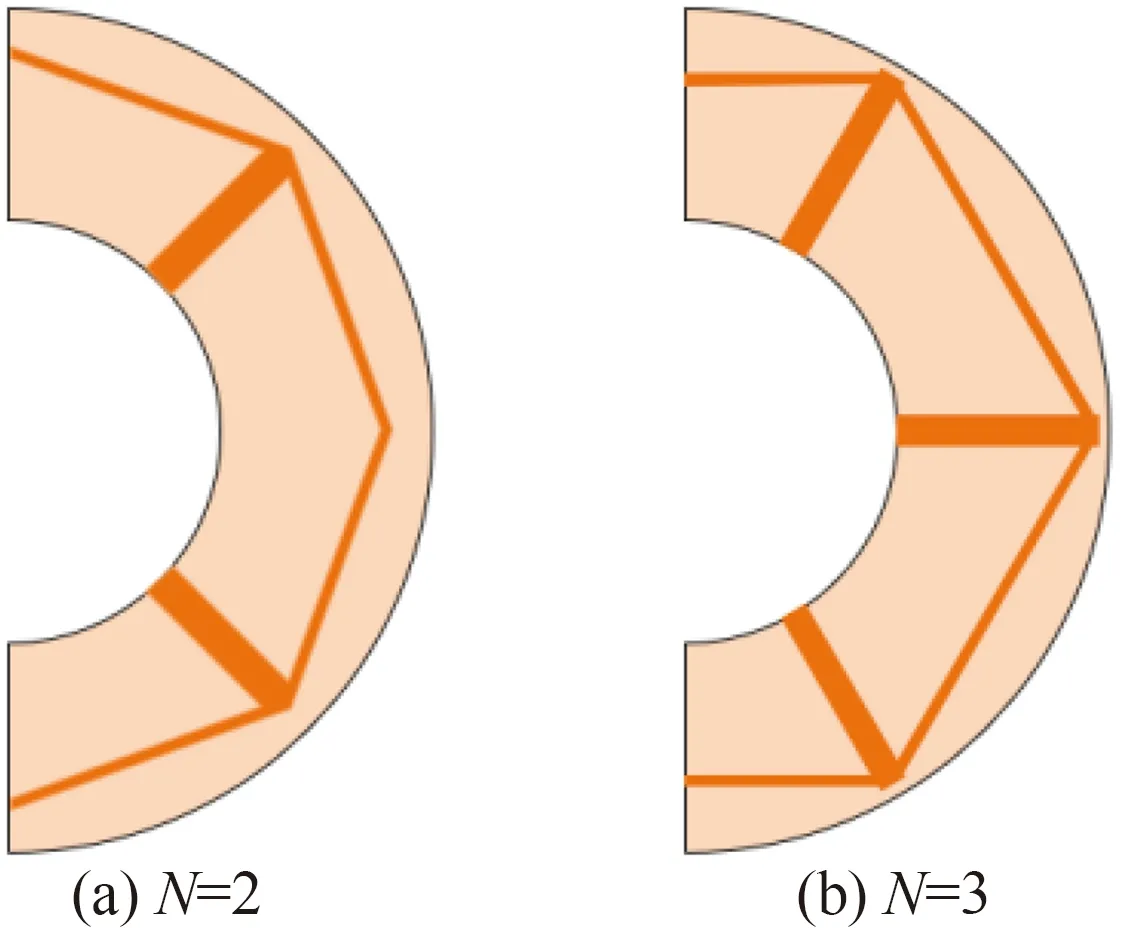
图13 优化后不同数量的翅片结构示意图Fig.13 Schematic diagram of different number of fins after optimization

表2 不同数量下优化后翅片结构参数Tab.2 Optimized parameters of fin structure under different numbers

对于给定的翅片占比，翅片数量的有利于翅片和相变材料之间的传热，也会造成翅片其他参数发生变化。例如随着翅片数量增加时，翅片的各分支宽度会减小，这会造成翅片的导热效率降低。图14 为不同翅片数量的储热器完全凝固时间，可以看出，随着翅片数量的增加，储热器的凝固效果有所提高；当翅片数量从1 增加到3时，储热器的完全凝固时间缩短了57.7%，这表明翅片数量增加造成的凝固速率的提高超过了由于翅片宽度减小造成的传热恶化问题。

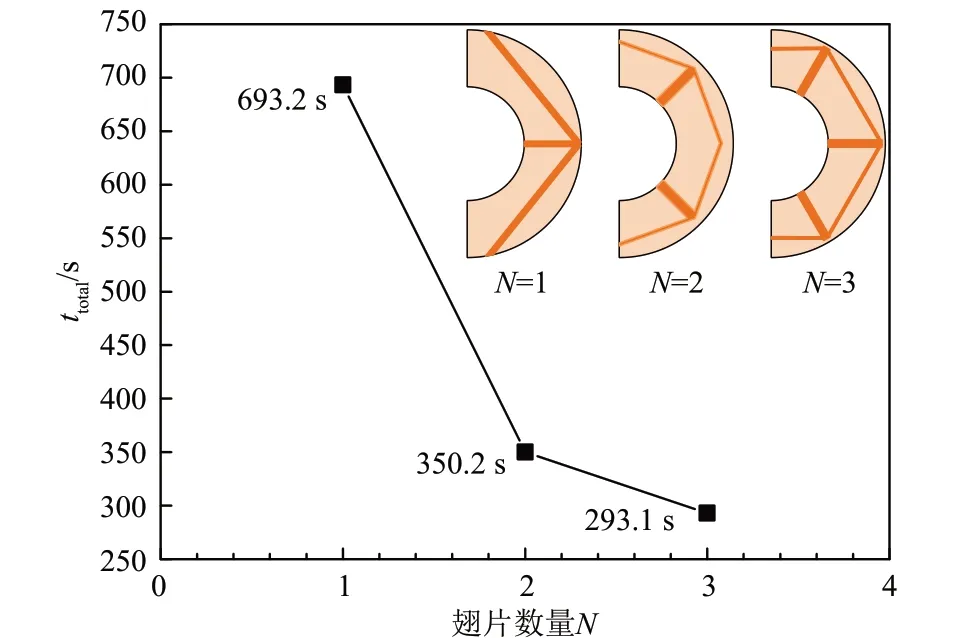
图14 不同翅片数量的储热器完全凝固时间Fig.14 Complete solidification time of heat storage with different number of fins

选取分支无量纲夹角为0.167、0.25、0.333、0.417、0.5，主翅的无量纲长度为0、0.1、0.3 的传统Y 形翅片与优化所得箭头形翅片进行对比研究。图15显示了不同数量、不同结构翅片储热器内相变材料到翅片和冷源(内管)的距离，可以看出，箭头形翅片储热器内相变材料到翅片和冷源的距离最短。图16显示了不同数量箭头形翅片与传统Y形翅片的完全凝固时间的对比，可以看出，箭头形翅片结构具有更好的强化效果，当翅片数量为2 时，相比于传统Y 形翅片，箭头形翅片结构可以使完全凝固时间缩短52.8%以上；当翅片数量为3 时，相比于传统Y 形翅片，箭头形翅片结构可以使完全凝固时间缩短41.3%以上。

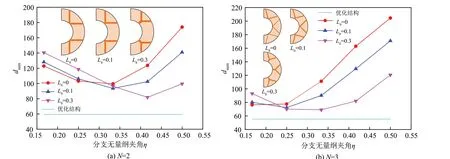
图15 不同数量、不同结构翅片储热器内相变材料到翅片和冷源的距离Fig.15 Distance between phase change material and fin and cold source in different number and structures of fin heat reservoir

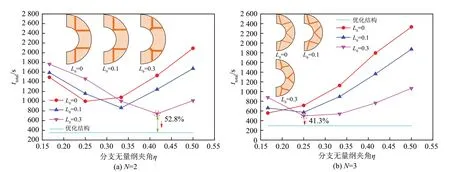
图16 不同数量、不同结构翅片储热器完全凝固时间Fig.16 Complete solidification time of finned heat reservoir with different number and structures

5 结论

翅片强化作用下的相变储热器对太阳能的大规模利用至关重要。为了提高相变储热器的能量释放性能，针对相变储热器内的翅片，提出了一种快速优化算法。该算法以相变材料到翅片和冷源的距离最短为优化目标，利用遗传算法对翅片的结构进行优化。以适用于凝固过程的管壳式相变储热器内一级Y 形翅片优化为例，在满足翅片材料用量一定的前提下，选择Y 形翅片的各分支长度、宽度比以及分支夹角作为设计变量。通过优化研究，得到以下结论：

1）通过快速优化算法优化后的翅片结构呈现箭头形。在所研究的放热工况下，相比于传统Y形翅片，当翅片数量为1～3时，箭头形翅片结构可以使完全凝固时间缩短41.3%～62.1%。

2）以相变材料到翅片和冷源距离最短作为优化目标具有一定的可行性，可以较好地对翅片结构进行优化。