方管中超声导波的传播特性及缺陷检测

刘美茹 万翔 张旭辉 陈渊 董明 樊红卫 毛清华 马宏伟

摘 要：針对基于点对点检测方式的传统体波方法在检测长距离方管时效率低下的问题，利用超声导波高效检测的优势，提出基于超声导波的方管检测方法。首先利用半解析有限元法求解出方管的相速度和群速度频散曲线，选择群速度频散曲线上群速度最大、相对平坦，频率范围在54～74 kHz的L（0，6）作为激励模态。其次分别采用有限元仿真和实验的方法，在方管中激励出中心频率为64 kHz的超声导波，研究导波在正常、面上存在圆孔缺陷和边缘存在槽缺陷的方管中的散射特性。在实验过程中，通过对压电晶片进行阻抗匹配来提高信噪比。仿真和实验结果表明，能够在方管中有效激励出L（0，6）模态超声导波，而且利用L（0，6）模态的缺陷反射回波，能够快速地检测出方管中的圆孔和槽缺陷，并定位缺陷的轴向位置。同时，阻抗匹配后信号的幅值是未阻抗匹配的2～3倍。纵向L（0，6）模态超声导波能够对方管中缺陷进行高效检测，为方管的检测提供了一种新的方法。

关键词：超声导波;方管;半解析有限元法;有限元仿真;阻抗匹配

中图分类号：TD 40            文献标志码：A

文章编号：1672-9315（2022）01-0143-09

DOI：10.13800/j.cnki.xakjdxxb.2022.0119开放科学（资源服务）标识码（OSID）：

Propagation characteristics of ultrasonic guided waves in square

tubes and its application to the detection of defects

LIU Meiru1，2，WAN Xiang1，2，ZHANG Xuhui1，2，CHEN Yuan1，2，DONG Ming1，2，

FAN Hongwei1，2，MAO Qinghua1，2，MA Hongwei1，2

（1.College of Mechanical and Engineering，Xi’an University of Science and Technology，Xi’an 710054，China;

2.Shaanxi Key Laboratory of Mine Mechanical and Electrical Equipment Intelligent Monitoring，

Xi’an University of Science and Technology，Xi’an 710054，China）

Abstract：It is inefficient to inspect long square tubes by using  traditional ultrasonic bulk waves  based on point-to-point inspection.In order to improve the efficiency of inspecting square tubes，ultrasonic guided wave method is proposed.Firstly，the phase and group velocity dispersion curves in square tubes are derived by semi-analytical finite element method.The longitudinal L（0，6）mode

is selected as the excitation mode with the group velocity value reaching the maximum，the group velocity dispersion curve being flat and the frequency ranging

from 54 to 74 kHz.Secondly，numerical and experimental studies are conducted respectively to investigate the excitation of longitudinal L（0，6）mode at the center frequency of 64 kHz in square tubes and to explore the propagation characteristics of ultrasonic L（0，6）mode guided waves in normal square tube，and in square tubes with circular through-hole damages located in surfaces and slot damages at edges.During the experiments，impedance matching is applied to piezoelectric transducers to improve the signal-to-noise ratio.Numerical and experimental results show that L（0，6）modal ultrasonic guided wave can be effectively excited in square tubes.Furthermore，the flaw reflection echo of L（0，6）mode can be used to effectively detect circular through-hole damages and slot damages at edges in the square tube，and to locate the axial position of the defects.Meanwhile，the amplitudes of the signals after impedance matching is improved by 2～3 times.The use of longitudinal ultrasonic guided wave of L（0，6）mode to detect damages in square tubes is quite  efficient.It provides a new effective alternative for the inspection of square tubes.Key words：ultrasonic guided wave;square tube;semi-analytical finite element method;finite element simulation;impedance matching

0 引 言

相比于圆管结构，方管结构由于其优越的抗弯性能，在建筑、机械、电力、化工等领域有着广泛的应用，如作为机场、高速公路、桥梁、电站设备、压力容器、石油储罐、起重运输机械等设施或设备的关键结构件[1]。为保证这些设施设备的安全运行，对方管结构的健康状况进行无损检测就显得尤为重要。目前国内外学者对方管结构的无损检测都做了相应的研究。张杰等对扶梯桁架开裂方管的失效分析中，对方管检测采用的是宏观检查的方法。这种目视的宏观检测方法能够有效检出方管外表面的宏观缺陷，而很难对较小表面裂纹进行检测，且无法检测出方管内部的缺陷[2]。刘小川等用射线检测的方法对外方内圆的超导导体方管焊缝做了检测，但是射线检测成本高且对人体有害[3]。高晓进等对复合材料方管的检测提出了超声对面内壁反射法，该方法采用液浸的方式进行耦合，适用于较小的试件检测[4]。传统的超声检测方法能够检测出方管的外部缺陷，也能够检测出方管的内部缺陷，并且具有较高的检测精度。然而，传统超声采用的是基于逐点检测的方式，在检测长达数米以上的方管结构时，则效率极端低下。因此，发展一种高效的方管无损检测方法尤为必要。超声导波是近年来兴起的一种新型高效的无损检测方法。它具有传播距离远、衰减小的特点，非常适用于横截面形状一致、轴向尺寸较长的固体材料[5-6]。目前，超声导波在板状[7-10]、圆管[11-13]、和钢轨[14-15]等结构的检测方面已有了非常广泛的应用。近年来，SOROHAN等利用有限元方法求解出方管结构中的频散曲线[16]。然而利用超声导波对方管进行检测时，选择何种模态的超声导波，以及能否在方管结构中有效地激励出超声导波并用于缺陷的检测，则研究较少。文中首先采用半解析有限元的方法，对方管的频散和多模态特性进行研究，并选择合适的激励模态和频率;然后通过实验和仿真验证所选的超声导波模态对方管结构检测的可行性和有效性。

1 方管结构频散和多模态特性分析文中的研究对象为长3 000 mm，截面为60 mm×60mm（长×宽），厚2 mm的直方管。材质为20#钢，弹性模量、泊松比和密度分别为210 GPa，0.3和7 900 kg/m3。相对于传统解析方法，半解析有限元方法能够对任意截面形状的结构，求解频散曲线。文中采用半解析有限元的方法求解方管的频散曲线[17-18]。图1为0～100 kHz时方管的群速度频散曲线图。由图1可知，①随着频率的增加，方管中频散曲线模态数量显著增加;②方管中频散曲线的模态相互重叠或相交;③许多模态在群速度频散曲线上有相应的峰值，但频率范围很小。这些复杂的频散和

模态特性使得选择合适的激励导波模态对方管进行检测时，变得极为困难。

仔细观察图1中0～100 kHz的群速度频散曲线，发现由红色框选中的54～74 kHz频率段内的模态，有较大的群速度值且速度变化较为平缓，这种模态便于在时域信号中与其他模态波形进行区分，可作为方管检验的激励模态。经过波结构分析为L（0，6）模态，所以，将L（0，6）作为激励模态，选取中心频率64 kHz作为激励信号的激励频率。

2 导波检测方管的仿真研究

2.1 仿真建模借助ABAQUS软件，在 ABAQUS/Explicit软件平台下，建立正常和存在圆孔缺陷及槽缺陷方

管的有限元模型。其中，方管截面边长a为60

mm、

壁厚h为2mm，长度L为3 000 mm。缺陷到

方管

左端面的距离为1 500 mm，圆孔缺陷直径d为10 mm，槽缺陷长度b为10 mm，槽宽w为2 mm。缺陷分别加工在方管边缘棱上和方管面中间，材料参数与求解频散曲线时材料参数一致。然后进行加载和模型的网格划分，激励信号频率为64 kHz，周期数为20;在方管左端面加载，接收节点集也设置在左端面，最后进行分析后处理。

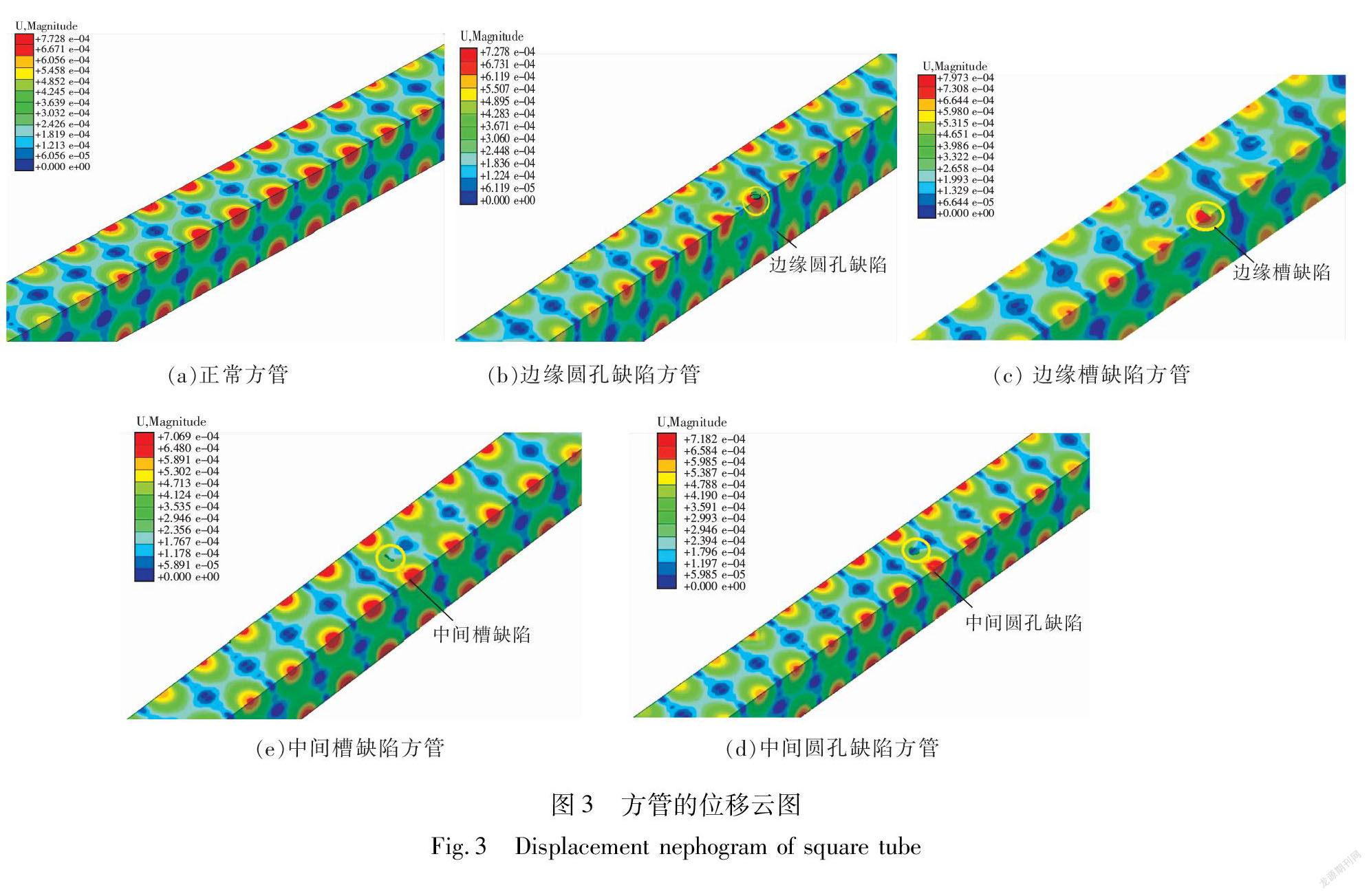
2.2 仿真结果及分析通过仿真的方法对如下5种情况进行分析对比：①正常方管结构;②边缘有圆孔缺陷的方管结构;③边缘有槽缺陷的方管结构;④面上有圆孔缺陷的方管结构;⑤面上有槽缺陷的方管结构，从而研究导波对方管边缘和面上缺陷的敏感性，仿真的位移云图如图3（a）～（e）所示，时域波形如图4所示，4种缺陷情况下反射波的幅值见表1。

分析图4可得，正常方管的时域波形图中第1个波是原始激励波，而第2个波是右端面的端面反射回波，波出现的时间在1.26×10-3 s处，方管总长3 000 mm，波速可由式（

1）计算得到

v=2×lt

1）式中 v为导波波速;l为距离方管左端面的距离;t为导波的传播时间。计算的导波传播速度为4 762 m/s，而从频散曲線中得到的激励模态群速度为4 700 m/s，计算出的实际速度与理论速度接近，群速度相对误差可由式（2）得到

（2）式中 x为计算值;x′为理论值;δ为相对误差。计算的导波群速度相对误差为1.32%，误差在允许范围内，从而验证了方管中激励的模态为L（0，6）模态。对比图4中正常和带缺陷方管的曲线波形图可知，图中第1个波为原始激励波，第3个波为右端面的反射回波，第2个波出现在6.3×10-4 s处，若为缺陷的反射回波，由式（

1）计算出回波出现的时间应在6.38×10-4 s处，计算理论时间与实际时间接近，所以，确定第2个波是缺陷的反射回波，且模态为L（0，6）。针对方管边缘和面上缺陷的敏感性分析，得到的结论如下。

1）正常结构中，边缘棱上的位移场的幅值要远大于面上的位移场幅值。

2）相同类型不同位置的缺陷，边缘棱上反射波的位移场幅值要大于面上反射波的位移场幅值，表明超声导波对边缘棱上缺陷更敏感。其原因还是由于边缘总的位移场幅值要大于面上总的位移场幅值（与结论

1）相符）。

3）相同位置不同类型的缺陷，圆孔缺陷反射波的位移场幅值要大于槽缺陷反射波的位移场幅值。主要原因是孔缺陷的面积要大于槽缺陷的面积，因此，对超声导波的反射更大。超声导波对圆孔缺陷更敏感。

4）超声导波对边缘槽缺陷和面上孔缺陷敏感性，受缺陷位置、缺陷类型和缺陷尺寸等多种因素的影响，不能完全确定超声导波对哪种情形更敏感。目前的缺陷尺寸情形下，由表1可知，超声导波对边缘槽缺陷反射波的幅值要大于对面上圆孔缺陷反射波的幅值。因此，在此条件下，超声导波对边缘槽缺陷的敏感性要大于面上圆孔缺陷的敏感性。

3 方管导波检测的实验研究经过仿真分析的验证，证明在方管中能有效激励出所选择的中心频率为64 kHz的L（0，6）模态超声导波，并能用于缺陷的检测。实验研究是在仿真研究的基础上，利用均匀布置在方管周向的压电晶片阵列激励出中心频率为64 kHz的L（0，6）模态超声导波，从而从实验的角度验证其可行性和有效性。仿真研究和实验研究是相互指导、相互验证的过程。

3.1 实验设置

3.1.1 实验对象分别对正常和有缺陷的方管进行实验，缺陷主要包括2种，一种是圆孔状缺陷，另一种是槽缺陷。圆孔状缺陷设置在方管的面上，形状如图5（a）所示，轴向位置如图5（c）所示，改变圆孔缺陷时只改变圆孔直径d。槽缺陷设置在方管的边缘棱上，形状如图5（b）所示，轴向位置如图5（c）所示，改变槽缺陷时只改变槽缺陷的长度b，槽宽w不变，为2 mm。

实验采用的激励信号是经Hamming窗调制的20周期正弦信号，该信号由上位机软件Ultra Station编辑，经信号发生器产生，幅值为5 V。

3.1.2 实验流程实验仪器包括电脑，信号发生器、示波器、阻抗分析仪、电压放大器、50Ω电阻、转换开关、压电晶片和方管，实验平台如图6所示。压电晶片作为传感器激励和接收超声导波，尺寸为30 mm×5 mm×0.5 mm，共有24片，均匀贴在方管一端，每面均布6个，总体成对称分布，以此来激励轴对称的纵向模态导波，压电晶片的粘贴结果如图7所示。

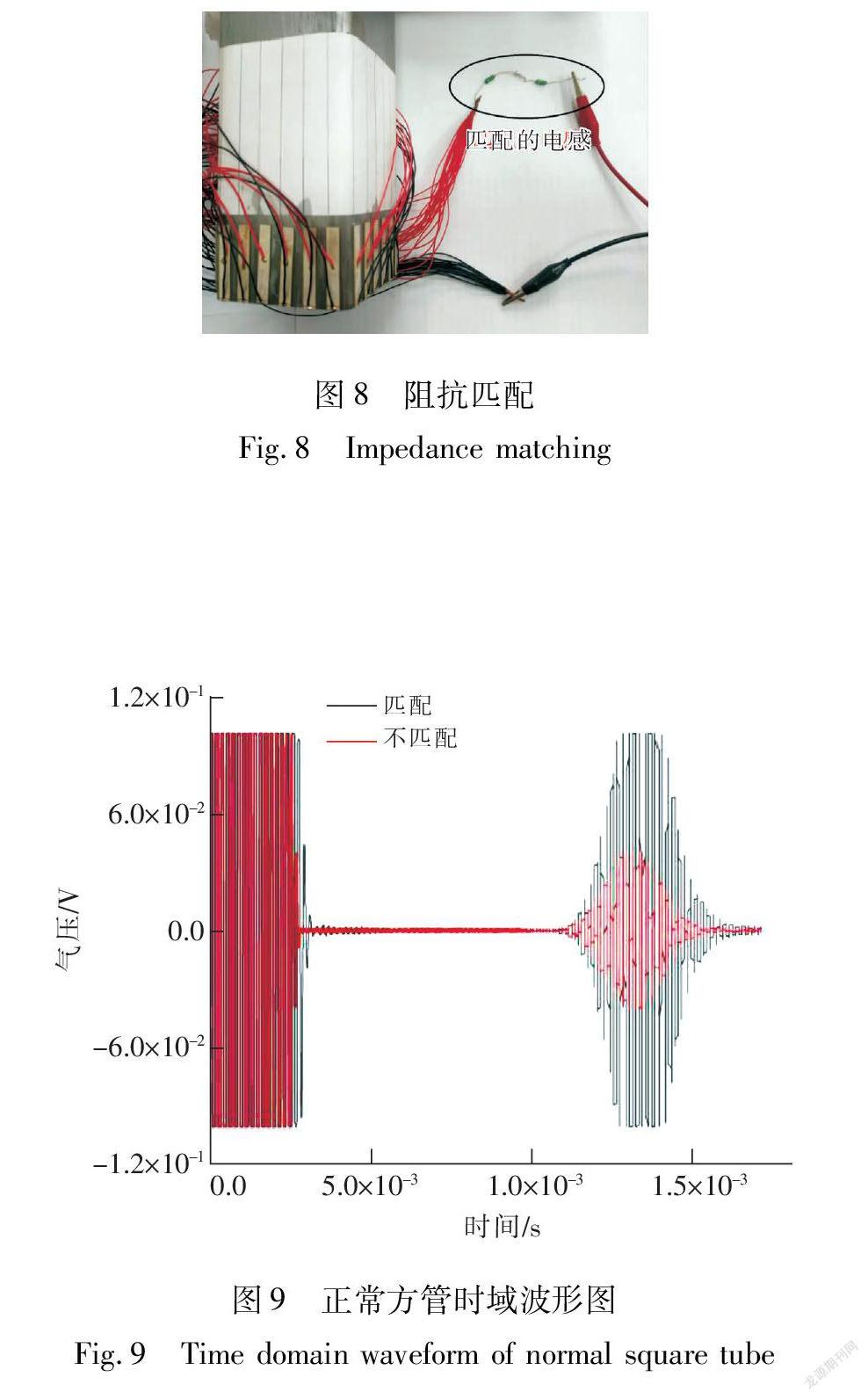
3.2 实验结果及分析实验中为了提高反射超声导波的信噪比，进行了阻抗匹配。阻抗匹配可以提高压电晶片的传输效率，从而实现更好的信噪比。粘贴24片压电晶片后的方管阻抗由阻抗分析仪测得，频率在64 kHz时，测得的阻抗值是2.15-j57.96 Ω，表现为容性。采用Smith圆进行匹配，将电感串联在压电晶片两端，使阻抗虚部趋近于0。经过Smith圆的匹配，得到一个最优电感142 μH。实验中阻抗匹配就是将142 μH的电感串聯在粘贴于方管的压电晶片两端，阻抗匹配的实验图如图8所示。

通过阻抗匹配使得压电晶片阵列和方管结构的声阻抗更加接近，从而使所激励的L（0，6）模态超声导波能够更有效地耦合到方管结构中。因而，阻抗匹配后的端面反射波显示出更大的幅值和更高的信噪比。由图9可知，第2个波出现的时间与仿真结果基本相同，是右端面的端面反射回波。进行阻抗匹配之后，右端面的反射回波幅值

明显增大，是未进行阻抗匹配反射回波幅值的2倍多。

3.2.1 圆孔状缺陷对存在圆孔状缺陷的方管进行实验并分析实验数据，提取激励波和第1个端面反射回波之间的数据，分析得到的时域波形图，判断方管中是否存在缺陷以及缺陷的位置和数量等。

1）方管中存在一个圆孔缺陷。在方管的1 500 mm处即A点存在不同大小的孔状缺陷，缺陷直径d分别为6，8，10和12 mm，激励频率为64 kHz时6和12 mm缺陷所得到的波形图，如图10所示。

分析图10，可看出原始激励波和右端面反射回波之间出现了一个波，经式（

1）计算得，L（0，6）模态波的传播时长为6.38×10-4 s，图上波出现的时间为6.3×10-4 s左右，验证该波是L（0，6）模态在A点缺陷的反射回波，所以超声导波可以检测到方管面上的圆孔缺陷。同时，图10（a）中未进行阻抗匹配的缺陷波较小，基本被被淹没在振动噪声中，图10（b）未进行阻抗匹配的缺陷波可被观察到，而经过阻抗匹配后缺陷反射回波的幅值显著增大，均可被观察到。不同大小圆孔缺陷的反射波幅值如图11所示。图11（a）是未进行阻抗匹配的缺陷幅值图，图11（b）是阻抗匹配后缺陷的幅值图，圆孔缺陷波幅值随缺陷尺寸的增大而增大，阻抗匹配后缺陷幅值明显大于未进行阻抗匹配的幅值，至少是未进行阻抗匹配幅值的2倍。由图12（a）可以看出，端面反射回波之前出现2个反射回波，反射波1出现的时间是3.18×10-4 s，经公式（

1）计算，其对应位置在距离左端面757.1 mm处，经公式（2）计算与B点的相对距离误差为0.9%，误差在允许范围内，所以，反射波1为B点缺陷的反射回波。传播时长为6.25×10-4 s的反射波2距离左端面1 488.1 mm，与A点的相对距离误差为0.8%，所以，反射波2为A点缺陷的反射回波。由此可知超声导波可以检测出方管面上存在的2个圆孔缺陷，并可以确定其轴向位置。图12（b）中反射波1和反射波2同图12（a），反射波3的传播时长为9.4×10-4 s，经计算得其位置距离左端面2 238.09 mm，与C点的相对距离误差为0.5%，所以，反射波3是C点缺陷的反射回波。所以，超声导波可以检测出方管面上存在的3个圆孔缺陷，并可以确定其轴向位置。

3.2.2 槽缺陷对存在槽缺陷的方管进行实验并分析实验数据，提取激励波和第1个端面反射回波之间的数据，分析得到的波形图，从而判断方管中是否存在槽缺陷以及缺陷位置和数量等。

1）方管上存在一个槽缺陷。方管上只有D点处存在槽缺陷，且槽缺陷的长度b分别为6，8，10和12 mm，槽宽w均为2 mm。6和12 mm长的槽缺陷得到的时域波形如图13所示。

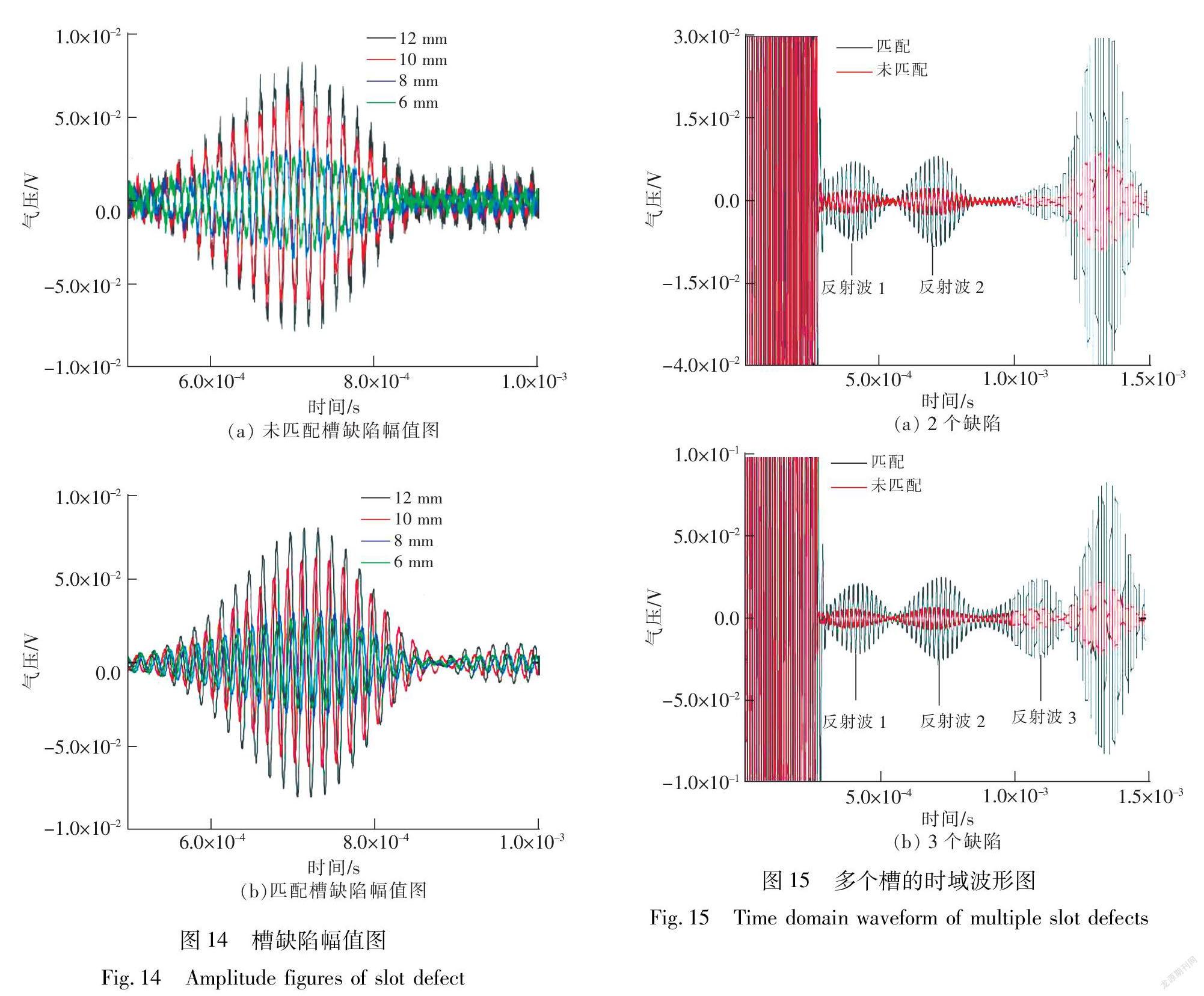
由图13可知，在右端面反射回波之前出现了波形，经计算可得，是方管D点缺陷的反射回波，所以，超声导波可以检测到方管边缘棱上的槽缺陷。不同尺寸槽缺陷的反射波幅值图如图14所示：图14（a）是未进行阻抗匹配的缺陷幅值图，图14（b）是阻抗匹配后缺陷的幅值图，槽缺陷反射波幅值随缺陷尺寸的增大而增大，阻抗匹配后的槽缺陷幅值至少是未进行阻抗匹配幅值的3倍。

2）方管上存在多个槽缺陷。存在2个槽缺陷时，D点槽为14 mm，E点槽10 mm;而存在3个槽缺陷则是D，E点槽尺寸与存在2个槽缺陷时相同，且F点存在10 mm的槽缺陷，且槽宽w均为2 mm。缺陷反射回波如图15所示。

由图15可得，利用公式（1）、（2）计算得到反射波1，2，3的位置分别在距离左端面745.25，1 506.45，2 276.57 mm处，与点D，E，F的相对距离误差分别为0.6%，0.4%，0.8%，误差均在允许范围内，所以，反射波1为E点槽缺陷反射回波，反射波2为D点槽缺陷反射回波，反射波3为F点槽缺陷反射回波。超声导波可以清楚的检测出方管上存在的2个和3个槽缺陷的情况，并能确定出其轴向位置。且发现：反射波2的幅值比反射波1的幅值大，因为D点缺陷大小为14 mm，而E点缺陷大小为10 mm。综上，超声导波可以检测出方管上圆孔状缺陷和槽缺陷，也可以检测到方管上同时存在的多个缺陷，所以可以用超声导波L（0，6）模态对方管进行缺陷检测。同时，采取阻抗匹配可以提高信号的信噪比，使得到的反射回波幅值增大，检测效果更好。

4 结 论

1）方管结构的频散曲线模态特性比相应尺寸圆管结构的模态特性要复杂的多。通过分析，选择群速度频散曲线上群速度速度较大、相对平缓的频率范围在54～74 kHz的L（0，6）作为激励模态。

2）利用超声导波L（0，6）激励模态检测不同类型和不同位置的缺陷，而且对不同类型和位置缺陷的敏感性不同。相同类型的缺陷，超声导波对边缘棱上缺陷的敏感性更大;相同位置的缺陷，超声导波对圆孔缺陷的敏感性更大。

3）利用阻抗匹配可以提高实验信号的信噪比，检测效果更好。进行阻抗匹配后，得到的反射回波信号幅值增大，实验结果表明：阻抗匹配后的缺陷反射回波幅值至少是未进行阻抗匹配缺陷反射回波幅值的2倍。4）仿真和实验验证表明，相比于点对点的传统超声检测，纵向L（0，6）模态超声导波能够对方管中缺陷进行高效检测，是一种对方管结构进行检测可行且有效的方法。

参考文献（References）：

[1]

柴昶，刘迎春.钢结构工程中方（矩）形钢管的应用及其材性特点[J].钢结构，2009，24（1

1）：53-60.

CHAI Chang，LIU Yingchun.Application and Performance features of square（rectangular）steel tube in steel structure[J].Steel Construction，2009，24（1

1）：53-60.

[2]張杰，吴继权.扶梯桁架开裂失效分析[J].中国特种设备安全，2018，34（5）：54-58，73.ZHANG Jie，WU Jiquan.Failure analysis on crack of escalator truss[J].China Special Equipment Safety，2018，34（5）：54-58，73.

[3]刘小川，武玉，万永升，等.ITER超导导体方管铠甲焊缝的射线检测[J].无损检测，2013，35（5）：59-61，80.

LIU Xiaochuan，WU Yu，WAN Yongsheng，et al.Non-destructive examination on PF butt welds of ITER superconducting conductor[J].Nondestructive Testing，2013，35（5）：59-61，80.

[4]高晓进，周金帅，张铁夫.小截面方管结构CFRP复合材料的超声检测方法[J].声学技术，2019，38（

1）：58-61.GAO Xiaojin，ZHOU Jinshuai，ZHANG Tiefu.Ultrasonic testing method for CFRP composites of small section square tube structure[J].Technical Acoustics，2019，38（

1）：58-61.

[5]杨斌，胡超杰，轩福贞，等.基于超声导波的压力容器健康监测Ⅰ：波传导行为及损伤定位[J].机械工程学报，2020，56（4）：1-10.

YANG Bin，HU Chaojie，XUAN Fuzhen，et al.Structural health monitoring of pressure vessel based on guided wave technology.Part I：Wave propagating and damage localization[J].Journal of Mechanic Engineering，2020，56（4）：1-10.

[6]LING E H，RAHIM R A.A review on ultrasonic guided wave technology[J].Australian Journal of Mechanical Engineering，2020，18（1）：32-44.

[7]WAN X，TSE P W，ZHANG X，et al.Numerical study on static component generation from the primary Lamb waves propagating in a plate with nonlinearity[J].Smart Materials and Structures，2018，27（4）.

[8]DE LUCA A，CAPUTO F，SHARIF KHODAEI Z，et al.

Damage characterization of composite plates under low velocity impact using ultrasonic guided waves[J].Composites Part B，2018，138：168-180.

[9]譚海辉，陶唐飞，徐光华，等.翅片管式蒸发器超声波除霜理论与技术研究[J].西安交通大学学报，2015，49（9）：105-113.

TAN Haihui，TAO Tangfei，XU Guanghua，et al.Ultrasonic Defrosting Theory and Technology for Finned-Tude Evaporator[J].Journal of Xi’an Jiaotong University，2015，49（9）：105-113.

[10]杨理践，邢燕好，张佳，等.基于电磁超声导波的铝板裂纹缺陷检测方法[J].仪器仪表学报，2018，39（4）：150-160.

YANG Lijian，XING Yanhao，ZAHNG Jia，et al.Crack defect detection of aluminum plate based on electromagnetic ultrasonic guided wave[J].Chinese Journal of Scientific Instrument，2018，39（4）：150-160.

[11]周进节，郑阳，张宗健，等.基于电磁超声换能器阵列的管道螺旋导波传播规律研究[J].机械工程学报，2018，54（22）：38-46.

ZHOU Jinjie，ZHENG Yang，ZHANG Zongjian，et al.Helical mode guided waves in pipe observed by electromagnetic acoustic transducer array[J].Journal of Mechanic Engineering，2018，54（22）：38-46.

[12] GUAN R Q，LU Y，WANG K，et al.Fatigue crack detection

in pipes with multiple mode nonlinear guided waves[J].Structural Health Monitoring，2019，18（1）：180-192.

[13]GUO S F，CHEN S，ZHANG L，et al.Direct-write piezoelectric ultrasonic transducers for pipe structural health monitoring[J].NDT and E International，2019，107.

[14]朱力强，许西宁，余祖俊，等.基于超声导波的钢轨完整性检测方法研究[J].仪器仪表学报，2016，37（7）：1603-1609.

ZHU Liqiang，XU Xining，YU Zujun，et al.Study on the railway integrity monitoring method based on ultrasonic guided waves[J].Chinese Journal of Scientific Instrument，2016，37（7）：1603-1609.

[15]SHI H M，ZHUANG L，XU X N，et al.An ultrasonic

guided wave mode selection and excitation method in rail defect detection[J].Applied Sciences，2019，9（6）：1170.

[16]SOROHAN S，CONSTANTIN N，GAVAN M，et al.Extraction of dispersion curves for waves propagating in free complex waveguides by standard finite element codes[J].Ultrasonics，2011，51（4）：503 515.

[17]CONG M，WU X J，LIU R.Dispersion analysis of guided waves in the finned tube using the semi-analytical finite element method[J].Journal of Sound and Vibration，2017，401：114-126.

[18]HAYASHI T，SONG W J，ROSE J L.Guided wave dispersion curves for a bar with an arbitrary cross-section，a rod and rail example[J].Ultrasonics，2003，41（3）：175-183.

1899501705269