基于供应链结构的共享折扣策略研究
2022-03-16曹庆宁杜嘉浩余玉刚孙李波
曹庆宁 杜嘉浩 余玉刚 孙李波
(中国科学技术大学管理学院)
1 研究背景
随着移动支付等互联网技术不断普及,对产品或服务的供需双方同时提供折扣或补贴,成为平台型企业快速发展的重要手段之一,如天猫、货拉拉等。受此启发,越来越多的制造商尝试在产品包装上置入二维码等产品识别信息,并通过鼓励零售商和消费者扫描二维码后获得一定比例的产品折扣的形式开展产品促销,称之为共享折扣策略。以本研究所合作的一家全国知名的休闲食品制造商ZX的共享折扣策略为例:ZX在产品包装内附加二维码,当产品成功售出后,零售商和消费者可通过扫码各自获取一定比例的折扣。
制造商通过共享折扣策略对下游零售商和消费者进行促销时,需要考虑产品生产成本和折扣分配比例对供应链各成员间利润的影响。首先,由于制造商所提供的折扣可看作产品的促销成本,因此,较高的产品生产成本将直接压缩企业采纳共享折扣策略时的潜在利润空间;其次,需要考虑折扣分配比例对营销效果的调节作用。当消费者所能获得的折扣分配比例较低时,共享折扣策略无法吸引到足够多的消费者购买该商品,此时共享折扣策略对需求端的促进作用非常有限;反之,当消费者所能获得的折扣比例较高但零售商所能获得的比例较低时,则会很大程度上打击到零售商的积极性。围绕上述关注点,本研究针对由单个制造商和单个零售商组成的供应链结构,首先分析折扣分配比例对制造商最优批发价和零售商最优订货量的影响;其次,将共享折扣策略与两种非常经典的制造商折扣策略(批发价折扣策略和余货补偿策略)进行比较,找到共享折扣策略的具体适用条件;最后,基于所合作的休闲食品企业ZX的部分运营数据进行算例分析,旨在帮助企业厘清共享折扣策略的适用条件,为企业促销实践提供指导。
目前,针对共享折扣策略的理论研究还相对较少。基于BLATTBERG等[1]关于促销激励类型的定义,本研究从面向零售商的促销激励以及面向消费者的促销激励两方面展开文献回顾。首先,在面向零售商的促销研究中,学者们主要关注制造商如何通过激励零售商订购更多产品来提高其自身利润。例如,NESLIN等[2]研究了当面对不同类型的零售商和消费者时,制造商对零售商的促销方式与消费者广告类型的匹配问题。KURATA等[3]提出,制造商对零售商售出产品实施激励的方式总能使制造商和整体供应链获益。YANG等[4]构建了将零售商提供全单位产品折扣与服务补贴比率相结合的制造商两期博弈模型。张娟等[5]研究发现,上游供应商的创新产品研发对下游产生了广告激励作用,并能刺激传统产品的销售。相关文献还从数量折扣[6]、销售折扣[7]、退货策略[8]等角度研究了面向零售商促销对供应链成员带来的影响。其次,在面向消费者的促销研究中,学者们主要关注制造商如何通过促销刺激消费者产生购买行为。CHO等[9]在竞争环境下探讨双层供应链结构中制造商为消费者提供折扣的条件。周丹等[10]在消费者预算约束条件下研究了企业推荐奖励策略所带来的营销效果。许明辉等[11]发现,当零售商对市场需求预测精度较低时,零售商和供应商都偏好供应商促销模式。毛照昉等[12]指出在两期销售情况下,当第一期消费者数超过第二期一定数量时,对第二期消费者采取折扣低价销售更优。ARYA等[13]发现,制造商可以通过向消费者提供产品折扣来增加需求,进而降低零售商的战略库存。代建生[14]提出,零售商风险中性情况下供应商分担促销成本可以实现供应链的协调。慕银平等[15]研究发现,生产商选择分摊消费者折扣券方法成本时,可以在保证零售商利润的前提下增加供应链利润。此外,相关的促销场景还包括以旧换新策略[16,17]、优惠券策略[18]、邮件返款策略[19]等,或将消费者促销策略作为价格歧视的主要工具[20]等。
上述文献主要从零售商促销或消费者促销的单一角度展开分析,与之不同,本研究的共享折扣促销策略中,制造商可通过二维码等信息技术对零售商和消费者进行同时激励。此外,一部分学者也针对零售商和消费者同时进行促销的场景进行了研究,探讨制造商对零售商和消费者同时开展促销给供应链利润等方面带来的影响[21~23],但这些研究未涉及折扣分配这一情境。本研究在此基础上,进一步探讨促销折扣的分配比例对制造商和零售商的决策影响,并将共享折扣策略与经典的批发价折扣策略和余货补偿策略的各自适用范围进行了比较。本研究的意义在于,从制造商、零售商以及消费者间的交互关系出发,剖析共享折扣促销策略对制造商批发价决策以及零售商订货量决策的影响,进而厘清共享折扣促销策略可为制造商和零售商带来利润提升的条件。
2 共享折扣促销策略
考虑由单个制造商和单个零售商组成的供应链结构(见图1),其中实线表示产品流,虚线表示资金流。制造商为零售商所售出的每单位产品提供的总折扣金额为r,其中分配给消费者的折扣分配比例为λ(简称为折扣分配比例),分配给零售商的折扣分配比例为1-λ。将产品的单位生产成本记为c,制造商在销售过程中需要制定其批发价格决策w。随后,零售商向制造商订货并制定订货量决策Q,并以零售价p进行销售。为了简化并专注于对共享折扣促销策略进行分析,本研究沿用相关的促销策略研究中的设定[24~27],假设零售价格p由外部的市场竞争决定。


本研究的场景与YUAN等[28]、TSAO等[29]的研究类似,均探讨由单个制造商和单个零售商组成的双层供应链结构中的制造商促销策略,因此参照上述文献中的设定,对市场中的不确定性需求进行刻画。将需求函数设置为D=f(p)+U,其中,f(p)=a-bp且a>0,b>0;U为一个连续的随机变量且服从区间[-(a-bp),a-bp]内的均匀分布,因此,市场需求D均匀分布于区间[0,2(a-bp)]内。该设定可直观理解为:当产品价格降低时,整个市场的需求不确定性会因为潜在消费者增多而变大。考虑到共享折扣促销策略下消费者购买产品实际支付的成本为p-λr,故共享折扣促销下市场需求在区间[0,2(a-b(p-λr))]内均匀分布。为方便理解模型构建求解过程,相关符号说明见表1。

表1 符号及说明

π(Q)=(p+(1-λ)r)E(D|D≤Q)+
(p+(1-λ)r)E(D|D>Q)-Qw。
(1)
对制造商而言,一方面可从产品销售中直接获益,另一方面也需要支付相应的产品折扣金额,由此可以将制造商利润函数表示为
Π(w)=(w-c)Q(w)-rE(D|D≤
Q(w))-rE(D|D>Q(w)) 。
(2)
通过两阶段Stackelberg博弈模型对制造商和零售商的决策进行分析,即制造商首先制定产品的批发价,零售商随后决定其订货量。采用逆向归纳法对模型求解,并用上标s对共享折扣策略的决策变量进行标识,通过式(1)可获得零售商最优订货量关于批发价格的等式Q(w),代入式(2)后可求解出制造商最优批发价格w,最终求解结果见命题1。
命题1在实施共享折扣促销策略情形下,ws=(p+r-λr)(p+c+r-λr)/(2p+r-2λr);Qs=2(p-c-λr)(a-bp+bλr)/(2p+r-2λr);Πs=(p-c-λr)2(a-bp+bλr)/(2p+r-2λr);πs=(p-c-λr)2(p+r-λr)(a-bp+bλr)/(2p+r-2λr)2。
由命题1可知,产品成本c、单位产品折扣金额r和折扣分配比例λ对零售商订货量决策和制造商批发价格决策均有显著影响。这些因素的单调性分析结果见命题2。另外需要指出,尽管折扣分配比例λ=0和λ=1分别对应制造商将所有折扣都分配给零售商或者都分配给消费者的特殊情形,制造商在共享折扣策略下的最优利润和最优决策变量,都不是这两种情境下的最优利润或最优决策变量的线性组合,根本原因在于,折扣分配比例λ不仅会影响消费者的需求以及该部分需求所对应的零售商订货决策,还会对零售商本身的利润结构造成影响。
命题2在共享折扣促销策略下,ws和Qs对于c、r以及λ的单调性分析结果如下:①∂ws/∂c>0,∂ws/∂r>0,∂ws/∂λ<0。②∂Qs/∂c<0;当c<(2b(p+r-λr)(p-λr)-ar)/(2a+br)时,∂Qs/∂λ>0,反之,∂Qs/∂λ<0;当λ>(a-bp)/2a且c<(br2λ2(2λ-1)+p2(b+2bλ)-p(a+4brλ2))/(bp+a(2λ-1))时,∂Qs/∂r>0,反之,∂Qs/∂r<0。
命题2表明,最优批发价格ws随着产品成本c和单位产品折扣金额r的增加而增加,这是由于生产成本c以及折扣力度r都是制造商在共享折扣策略下的主要成本,当产品成本升高或者折扣力度加大时,制造商的单位总成本也将显著升高,此时,提高批发价格可一定程度地帮助制造商提升单个产品的利润空间。除此之外,最优批发价格ws随着折扣分配比例λ的增大而减小,意味着当制造商将更高比例的折扣分配给消费者时,零售商从单个产品的销售中所能获得的利润空间也随之被压缩,为了提高零售商的积极性,制造商需要降低批发价格。
由命题2还可知,零售商的最优订货量Qs随着产品单位成本c增加而降低。其主要原因在于,当单位成本增加时,制造商提高批发价的举措会使得零售商的潜在利润空间被压缩。与此同时,最优订货量Qs依折扣分配比例λ的单调性受到了生产成本的调节,具体而言,当产品生产成本较低时,零售商的最优订货量随着折扣分配比例λ的增加而增加。该结论说明仅当产品成本较低时,制造商对消费者激励所带来的市场需求效应会显著提升零售商的订货量;反之在产品成本较高的情况下,制造商只有将更高比例的折扣分配给零售商,才会显著提升零售商的订货量。这也意味着,当产品的零售价格保持相对稳定的情况下,制造商可通过共享折扣策略下的不同折扣分配比例对零售商的订货行为进行引导。该命题还表明,只有在分配比例λ较高且产品成本c较低的情况下,订货量Qs才会随着单位产品折扣金额r的增加而增加。这意味着对于低成本产品而言,只有在消费者激励的有效性得到一定保障时,提高单位产品折扣金额r才能促使零售商增加订货量;反之,零售商将减少订货量。
3 策略对比分析
前文分析了产品成本、产品折扣金额和折扣分配比例对最优订货量及最优批发价格的影响。为了进一步探究共享折扣策略的适用条件,本节将引入两种与共享折扣互补性很强且非常经典的制造商折扣促销方式:批发价折扣策略[28, 30]和余货补偿策略[29]。从实际运作的角度而言,批发价折扣策略可看成是制造商对所有批发给零售商的产品进行折扣促销,共享折扣策略和余货补偿策略可分别看成制造商对由零售商成功售出以及未售出的产品进行折扣促销,因此,3种折扣策略之间具有很强的互补性。本节的分析对厘清3种折扣策略的互补性具有重要的实践意义。考虑到模型的可求解性以及能够更加专注地分析折扣模式对供应链决策、制造商利润和零售商利润带来的影响,假设各促销策略中折扣金额均外生为r,并将在后文中针对不同折扣金额r对共享折扣策略利润的影响进行数值分析。
3.1 传统促销策略模型

π(Q)=pE(D|D≤Q)+
pE(D|D>Q)-Q(w-r) ;
(3)
制造商通过产品销售收入扣除折扣支出后得到的利润为
Π(w)=(w-c-r)Q(w)。
(4)

π(Q)=pE(D│D≤Q)+pE(D│D>Q)+
rE(Q-D│D≤Q)-Qw;
(5)
制造商通过销售产品获得收入扣减其为零售商未售出产品提供的折扣,获得利润为
Π(w)=(w-c)Q(w)-rE(Q(w)-D|D≤Q(w))。
(6)
遵循先由制造商提出批发价格再由零售商确定订货量的Stackelberg博弈顺序,对如上两种传统策略进行分析,运用逆向归纳法对式(3)~式(6)进行求解,并采用上标o表示批发价折扣策略,上标b表示余货补偿策略,可获得两种促销策略下的均衡结果,整合共享折扣策略下均衡结果见表2。其中,批发价折扣策略下的制造商利润、零售商最优订货量及其利润均不受产品折扣金额的影响。这是由于当制造商为零售商所订购的每一单位产品均提供折扣时,增加一单位产品折扣金额r同样会增加一单位批发价格w,因而零售商的订货成本wo-r及订货量均不随产品折扣金额r改变。

表2 共享折扣策略、批发价折扣策略与余货补偿策略下的均衡结果
3.2 模型结果比较分析
需要指出,制造商在使用共享折扣策略时可同时对零售商和消费者进行激励,并且不同分配比例对消费者的购买意愿及零售商的潜在利润空间均有影响,这与批发价折扣和余货补偿两种策略仅对零售商进行激励的情形存在显著区别。由此,从理论的角度而言,共享折扣策略较传统策略具有更高的灵活性。为厘清共享折扣策略的适用条件,本研究将对上述3种策略进行比较。
3.2.1批发价格比较
根据表2中的结果,首先对制造商最优批发价格进行比较分析,结果见命题3。
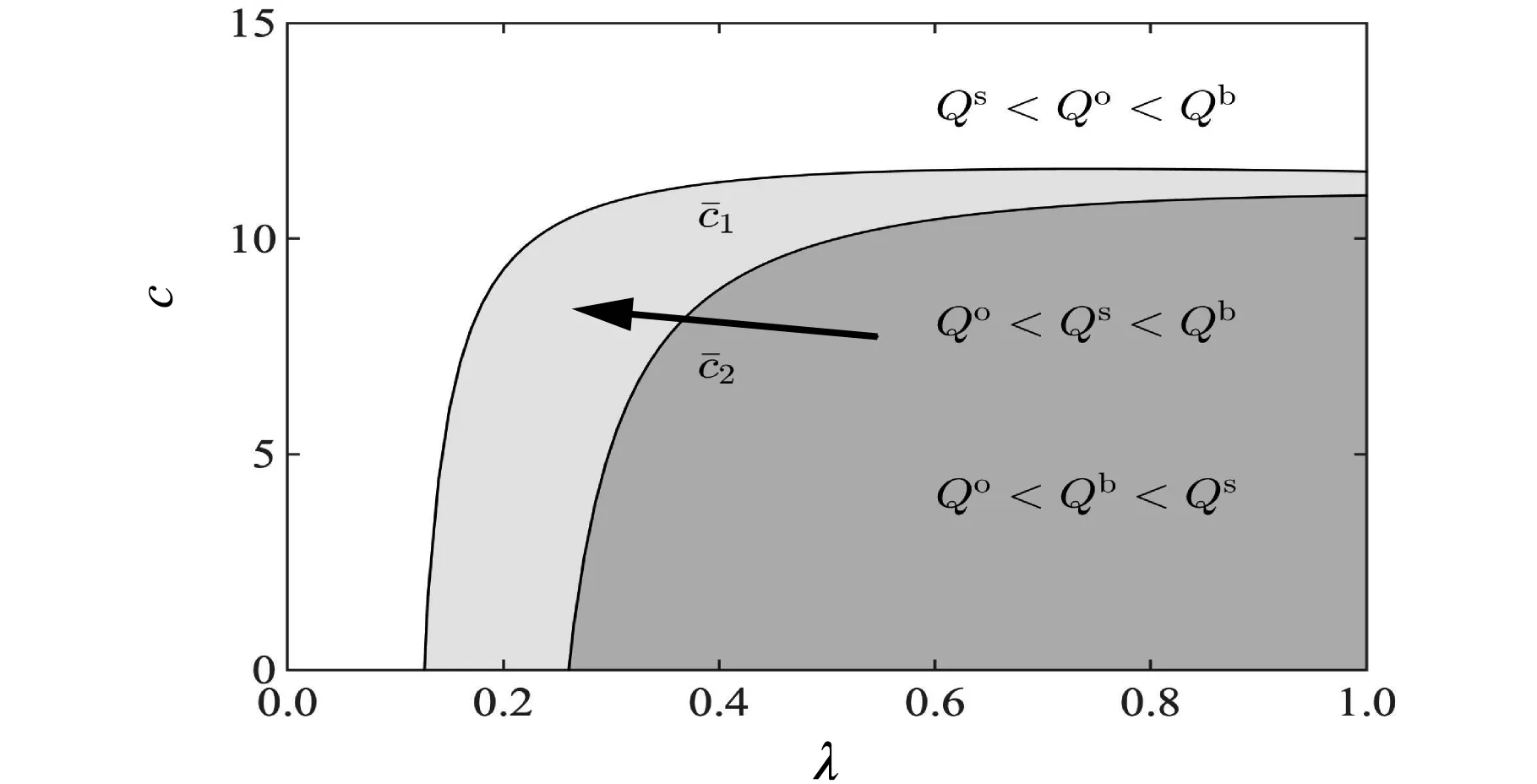
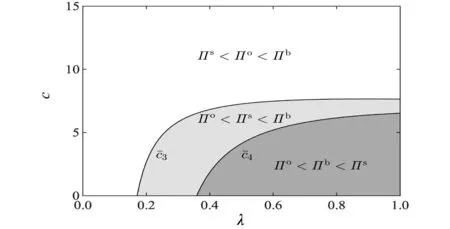
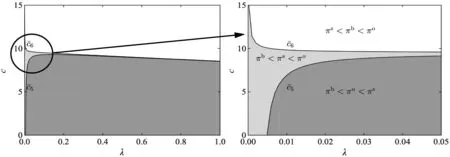
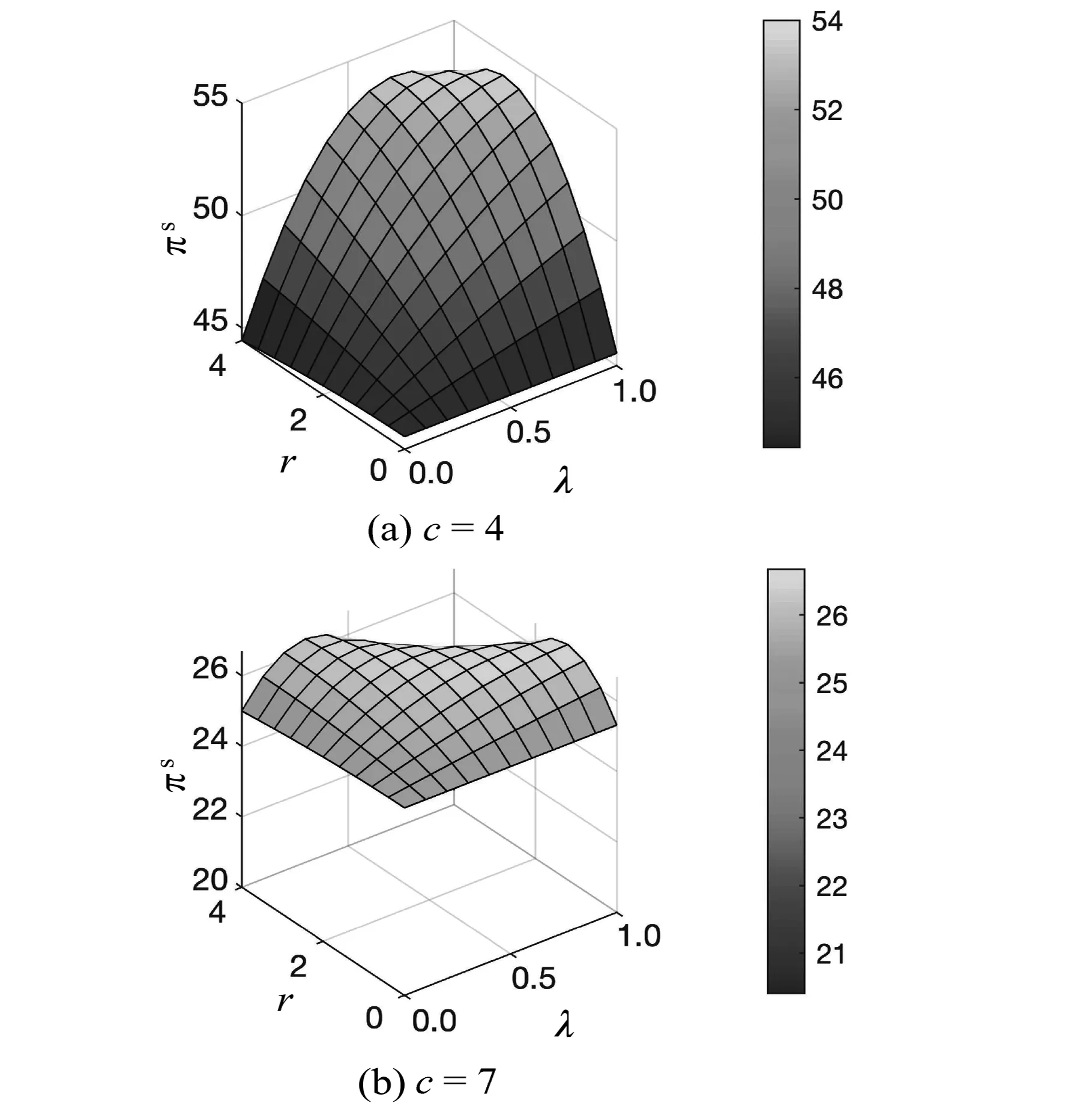
命题3共享折扣策略、批发价折扣策略和余货补偿策略下制造商最优批发价格大小关系为wb 命题3表明,制造商在批发价折扣策略下制定的最优批发价是3种折扣策略下最高的,其次是共享折扣策略,最后是余货补偿策略。这是由于制造商在批发价折扣策略下需要为所售出的每一件产品提供折扣,而在共享折扣和余货补偿两种策略下,仅分别对成功售出或者未售出的产品提供折扣,因此,其在批发价折扣策略下所需要付出的折扣成本支出相对较多,需要制定更高的批发价格来维持利润。 与余货补偿策略相比,无论订货量与市场需求的大小关系如何,零售商均可从共享折扣策略下成功销售的产品中获得对应折扣;而在余货补偿策略下,仅根据未售出产品的数量获得对应折扣补贴。由此可见,制造商在共享折扣策略下所付出的折扣支出成本较余货补偿策略更多,故不论分配比例大小如何,共享折扣策略下制造商制定的批发价格总高于余货补偿策略。 3.2.2订货量比较 由命题1和命题2可知,共享折扣策略下零售商最优订货量决策会受到分配比例影响,并且在不同产品成本条件下关于分配比例的单调性不同。通过对共享折扣策略下的最优订货量与其他两种策略下的最优订货量进行比较,可得命题4。 (7) (8) 图2 零售商订货量比较结果 3.2.3制造商利润比较 结合3种策略下最优批发价格和最优订货量的比较分析结果,进一步比较制造商利润,结果见命题5。 (9) (10) 由命题5可知,制造商在批发价折扣策略下的最优利润总是小于其在余货补偿策略下的最优利润。主要原因如下:一方面,制造商为所有产品提供折扣,等同于将其批发价决策过程中的一部分议价权让渡给零售商,此时,由于存在双重边际效应,所让渡的议价权并不能经零售商订货直接转换为制造商利润;另一方面,由于制造商在批发价折扣策略下制定了更高的批发价格,零售商据此所制定的订货量显著低于其在余货补偿策略下的订货量,进一步压缩了制造商在批发价折扣策略下的利润空间。 与命题4相似,制造商在共享折扣策略下的利润与其他两种策略下的利润大小关系,由产品生产成本和折扣分配比例共同决定。令a=100,b=5,p=16,r=1,制造商利润的比较结果见图3。 3.2.4零售商利润比较 零售商在上述3种策略下的利润比较结果见命题6。 (11) (12) 式中, (13) 图4 零售商利润比较结果 在前文的分析中,为了保证共享折扣、批发价折扣以及余货补偿3种折扣策略的横向比较公平性,将共享折扣策略的折扣金额r及其分配比例λ均设定为外生变量。考虑到现实情境下制造商既可选择分配更多折扣给消费者以增加市场需求,也可提高单位产品折扣金额提高整体的激励强度,下面通过数值分析探究在不同成本条件下,折扣金额和折扣分配比例两个系数的变动对共享折扣策略下的制造商与零售商利润的影响;并结合企业提供的实际数据,对市场需求参数、成本参数等进行近似拟合,从实例分析角度对企业折扣策略应用情况进行探索,为企业的策略选择提出参考性建议。 4.1 共享折扣策略利润数值分析 本节从单位产品折扣金额r以及折扣分配比例λ两个维度,对共享折扣策略下制造商利润Πs与零售商利润πs大小变化进行探究,设定基本参数为a=100,b=5,p=16,考虑产品成本c=4与c=7两种情形,结果分别见图5和图6。 图5 不同成本下折扣金额和折扣分配比例对制造商利润的影 由图5和图6中的r轴可观测到:当产品的折扣金额较低(靠近r=0的一侧)时,制造商利润和零售商利润均随着折扣分配比例呈上升趋势,即当制造商所销售产品的折扣金额较低时,无论是高成本产品(c=7)还是低成本产品(c=4),制造商都应该将更大比例的折扣金额分配给消费者,从而获得最佳的促销效果。反之,当产品的折扣金额较高(靠近r=4的一侧)时,制造商利润和零售商利润随着折扣分配比例呈先增后减的趋势,意味着持续为消费者提供更大比率的折扣不再是明智之举,此时,制造商需要同时兼顾该折扣促销策略对零售商的激励作用,从而制定出最恰当的分配比例决策。 由图5和图6中的λ轴可观测到:当折扣分配比例较低(靠近λ=0的一侧)时,制造商利润和零售商利润均随着产品折扣金额呈明显的下降趋势。该结果与命题2的结论一致,即在低折扣分配比例的情况下,制造商很难通过提高折扣金额达到提升零售商产品订货量的目的,此时,较高的折扣金额将使得制造商提高批发价格,零售商随后降低订货数量,最终造成二者利润同时减少的局面。反之,当折扣分配比例较大(靠近λ=1的一侧)时,制造商利润和零售商利润随着折扣金额呈先增后减的趋势,意味着制造商在采纳共享折扣策略时,需要谨慎选择折扣金额,而不能一味地增加折扣金额,或者单独对零售商与消费者中的一方进行促销。 4.2 企业折扣策略应用分析 本研究合作企业ZX是一家全国知名的休闲食品制造商,该企业于2019年4月~2019年9月期间,在线下销售渠道中实施了共享折扣促销策略。具体流程如下:ZX在产品包装内附加二维码,当产品经下游零售商成功销售给客户后,零售商和客户可通过扫描二维码获得部分的产品折扣。选择总销量最高的一种坚果类产品作为研究对象,并采用理论模型结合根据企业数据拟合所得的模型参数进行分析。首先,由于ZX采取建议零售价的模式对产品销售价格进行管理,故可通过企业数据得到零售价格p,进一步根据零售商产品订货量对参数a,b进行拟合并得到市场需求函数;其次,由于各零售商订货量规模有所差异,且不同零售商所负责的市场相互独立,选择排名前五且销量占比总计69.35%的零售商作为研究对象,编号为零售商1~5,并将对应的市场编号为市场1~5;最后,根据企业所提供信息将参数初步设定为r=3,λ=1/3,c=69.9。基于上述参数设定,制造商和零售商在不同市场中可选用共享折扣的边界条件及其利润变动情况见表3。 表3 拟合数据后各促销策略比较结果 由表3可知,ZX在市场2、4、5中通过使用共享折扣策略获得的最优利润,可高于批发价折扣策略和余货补偿策略下的最优利润,且利润提升幅度为2.59%~26.78%;与此同时,市场1、2、4、5中零售商通过共享折扣策略获得的最优利润也高于其他两种策略,利润提升幅度为1.31%~28.04%。由此,制造商ZX及其下游的零售商2、4、5均可通过采用共享折扣策略同时受益。 本研究针对制造商通过二维码等技术将产品折扣分配给零售商和消费者的共享折扣策略展开研究,构建了由单个制造商与单个零售商组成的供应链博弈模型,探究了产品成本、产品折扣金额以及折扣分配比例等要素,对制造商最优批发价、零售商最优订货量以及两者利润的影响。研究结果表明,产品成本和折扣分配比例对制造商的最优批发价和零售商最优订货量决策具有显著影响。当产品成本较低且分配给消费者的折扣比例较高时,制造商和零售商双方通过采用共享折扣策略,均可获得比传统的批发价折扣策略和余货补偿策略更高的利润。此时,将更高比例的共享折扣分配给消费者,可显著提高零售商的订货量。此外,通过数值分析,探究产品成本、折扣分配比例和折扣金额对共享折扣策略下制造商和零售商利润的影响发现,制造商需综合考虑折扣分配比例与折扣金额的影响,以选取合适的促销策略参数来最大化利润。本研究还尝试将理论研究结果用以指导企业实践,通过合作企业所提供的现实运营数据拟合模型参数,厘清了共享折扣策略在不同市场情况下的适用边界。 由于基于二维码等载体的共享折扣策略尚且属于比较新颖的营销模式,因此,存在较多的研究机会。首先,可以基于包括价格竞争或产量竞争在内的竞争性市场来深化对共享折扣策略的分析;其次,可以考虑非线性需求函数形式,或者基于消费者离散选择模型的共享折扣策略研究;最后,未来研究还可基于企业现实数据和场景,开展更为深入的数据驱动研究和探索。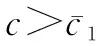


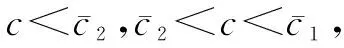
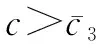
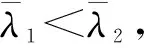




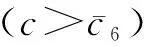
4 数值分析与讨论



5 结语
